高温气冷堆非纯氦气环境下高温合金碳迁移的化学动力学研究

郑伟; 李昊翔; 银华强; 何学东; 王秋豪; 马涛

doi:10.13832/j.jnpe.2021.05.0226

高温气冷堆非纯氦气环境下高温合金碳迁移的化学动力学研究

doi: 10.13832/j.jnpe.2021.05.0226

清华大学核能与新能源技术研究院，北京，100084

基金项目: 国家自然科学基金（11875176）；国家重大科技专项经费项目（ZX069）

详细信息

作者简介:
郑　伟（1997—），男，在读博士研究生，现从事高温堆内杂质腐蚀研究，E-mail: zhengw19@mails.tsinghua.edu.cn

通讯作者:
银华强，E-mail: yinhuaqiang@tsinghua.edu.cn

中图分类号: TL341
计量
- 文章访问数: 307
- HTML全文浏览量: 177
- PDF下载量: 48
- 被引次数: 0
出版历程
- 收稿日期: 2020-08-26
- 修回日期: 2021-02-26
- 刊出日期: 2021-09-30

Study on Chemical Kinetics of Carbon Migration in Superalloys in the Non-Pure Helium Environment in High Temperature Gas Cooled Reactors

Institute of Nuclear and New Energy Technology, Tsinghua University, Beijing, 100084, China

摘要

摘要: 高温气冷堆（HTGR）一回路冷却剂中的低含量杂质在HTGR超高温运行时会对堆内高温合金产生严重的腐蚀。其中高温合金与非纯氦气之间的碳迁移对于材料性能影响很大。本文探究了高温合金在非纯氦气环境中碳迁移的化学动力学原理，并基于此获得了判断材料脱碳和渗碳的理论判据。根据化学热力学和化学动力学原理，对非纯氦气环境的氧分压和碳活度进行了计算，指明CH₄与H₂O的分压比值较高时可能导致合金严重渗碳。在此基础上介绍了一种应用广泛的碳迁移模型——“铬的稳定相图”，分析了铬活度计算方法并归纳出取值建议。本文根据铬的稳定相图计算得到了清华大学设计的10 MW高温气冷堆（HTR-10）的实际运行工况下的腐蚀行为。
- 高温气冷堆（HTGR） /
- 高温合金 /
- 腐蚀 /
- 脱碳 /
- 渗碳
Abstract: The primary coolant in the high temperature gas cooled reactor (HTGR) contains impurities of low content, which will cause serious corrosion of the superalloys in the HTGR operating at the ultra-high temperature. In particular, the carbon migration between the superalloys and non-pure helium has a great influence on the material performance. This study explores the chemical kinetics principle of the carbon migration in the non-pure helium environment, from which the theoretical criteria for material decarburization and carburization are gained. Also, according to the chemical thermodynamics and kinetics principles, this study calculates the oxygen partial pressure and carbon activity in the non-pure helium environment, and indicates that a high partial pressure ratio of CH₄ to H₂O may lead to serious carburization of the alloys. On this basis, this study presents a widely used carbon migration model, “chromium stable phase diagram”, analyzes the chromium activity calculation method, and summarizes the recommended values. Finally, the corrosion behavior of the 10 MW HTGR (HTR-10) designed by Tsinghua University under the actual operating conditions is obtained by calculation based on the chromium stable phase diagram.
- HTGR /
- Superalloys /
- Corrosion /
- Decarburization /
- Carburization

HTML全文

图 1 甲烷对碳活度的影响

Figure 1. Effect of Methane on Carbon Activity

下载: 全尺寸图片幻灯片

图 2 碳活度和氧分压在氧化层中的变化

Figure 2. Changes in Carbon Activity and Oxygen Partial Pressure in the Oxide Layer

下载: 全尺寸图片幻灯片

图 3 合金的铬活度与温度的曲线

Figure 3. Chromium Activity and Temperature of Alloys

下载: 全尺寸图片幻灯片

图 4 Inconel617合金在950℃下的稳定相图

Figure 4. Stable Phase Diagram of Inconel617 at 950 ℃

下载: 全尺寸图片幻灯片

图 5 HTR-10的各气体组分在Inconel 617合金的铬稳定相图中的表示

Figure 5. Representations of Gas Compositions of HTR-10 in the Chromium Stable Phase Diagram for Inconel 617

下载: 全尺寸图片幻灯片

表 1 高温堆中各种合金的主要成分质量分数 %

Table 1. Mass Fraction of Main Compositions of Alloys in HTGR

高温合金类型	主要成分质量分数
高温合金类型	C	Ni	Fe	Cr
Inconel 617	0.08	Base	—	22
Nimonic 86	0.06	Base	—	25
Incoloy 800H	0.10	32	Base	20
Hastelloy X	0.08	Base	—	22
Hastelloy XR	0.07	Base	18.11	21.94
Base—基体，该元素为主要成分；“—”表示无含量

下载: 导出CSV

表 2 不同高温合金的铬活度取值

Table 2. Chromium Activity Values of Different Superalloys

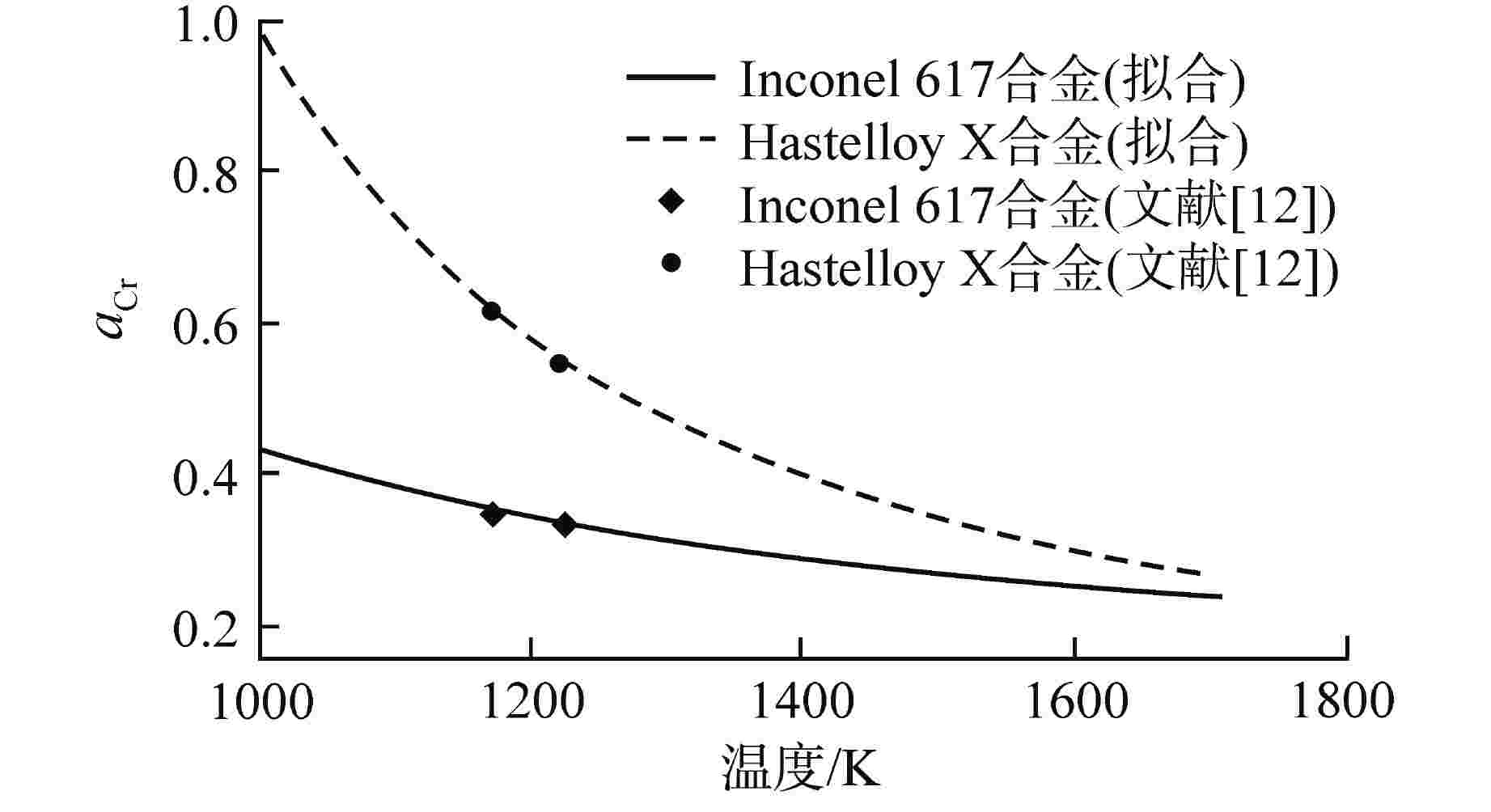
高温合金类型	a_Cr对数取值
Inconel 617	lg a_Cr$= 0.381 \times \left( { { {10000} \mathord{\left/{\vphantom { {10000} T} } \right.} T} } \right) - 3.673$
Nimonic 86	lg a_Cr$\approx 0.381 \times \left( { { {10000} \mathord{\left/{\vphantom { {10000} T} } \right.} T} } \right) - 3.673$
Hayens 230	ln a_Cr$ = 0.434 \times \left( { { {10000} \mathord{\left/{\vphantom { {10000} T} } \right.} T} } \right) - 3.897$
Hastelloy X	lg a_Cr$ = 0.315 \times \left( { { {10000} \mathord{\left/{\vphantom { {10000} T} } \right.} T} } \right) - 2.809$
Incoloy 800H	lg a_Cr$ \leqslant 0.315 \times \left( { { {10000} \mathord{\left/{\vphantom { {10000} T} } \right.} T} } \right) - 2.809$

下载: 导出CSV

表 3 HTR-10在750℃工况下氦气的杂质含量 ppm

Table 3. Impurity Content (ppm) of Helium in HTR-10 at 750℃

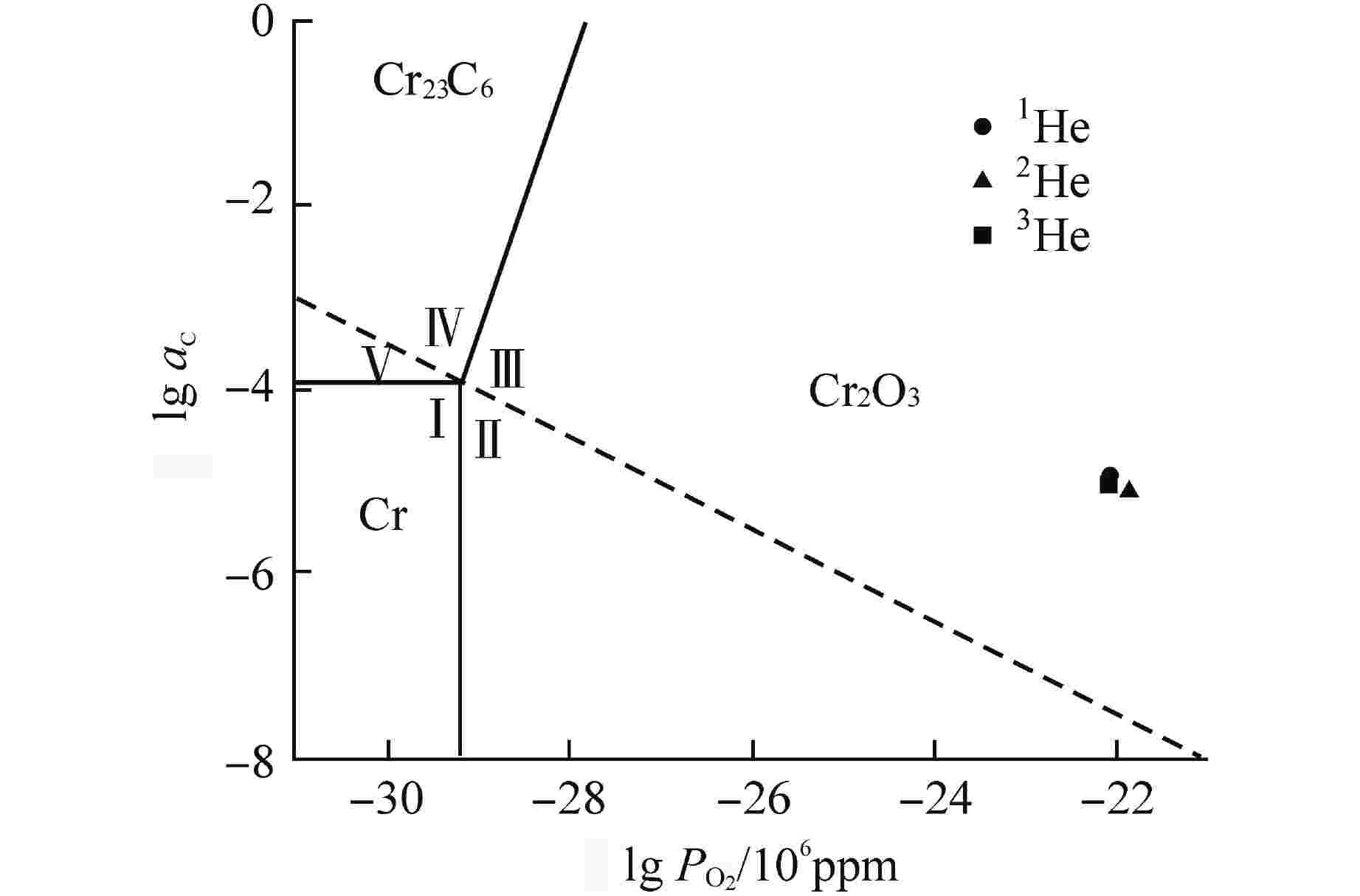
气体	H₂	CO	H₂O	CO₂	CH₄	O₂
¹He	2.43	2.01	0.1	1.85	0.36	0.34
²He	1.96	1.84	0.1	1.58	0.32	0.06
³He	2.46	1.69	0.1	1.58	0.37	0.42

下载: 导出CSV

参考文献(19)

[1]	SIMON R. The primary circuit of the dragon high temperature reactor experiment[C]//Proceedings of the 18th International Conference on Structural Mechanics in Reactor Technology. Beijing, 2005.
[2]	ZIERMANN E. Review of 21 years of power operation at the AVR experimental nuclear power station in Jülich[J]. Nuclear Engineering and Design, 1990, 121(2): 135-142. doi: 10.1016/0029-5493(90)90098-I
[3]	QUADAKKERS W J. High temperature corrosion in the service environments of a nuclear process heat plant[J]. Materials Science and Engineering, 1987, 87: 107-112. doi: 10.1016/0025-5416(87)90366-1
[4]	FUJIKAWA S, HAYASHI H, NAKAZAWA T, et al. Achievement of reactor-outlet coolant temperature of 950℃ in HTTR[J]. Journal of Nuclear Science and Technology, 2004, 41(12): 1245-1254. doi: 10.1080/18811248.2004.9726354
[5]	SAKABA N, NAKAGAWA S, FURUSAWA T, et al. Coolant chemistry of the high temperature gas-cooled reactor ‘HTTR’[J]. Transactions of the Atomic Energy Society of Japan, 2004, 3(4): 388-395. doi: 10.3327/taesj2002.3.388
[6]	LUO X W, YU X L, YU S Y. Oxidation performance of graphite material in reactors[J]. Frontiers of Energy and Power Engineering in China, 2008, 2(4): 471-474. doi: 10.1007/s11708-008-0074-6
[7]	YU X L, YU S Y. Analysis of fuel element matrix graphite corrosion in HTR-PM for normal operating conditions[J]. Nuclear Engineering and Design, 2010, 240(4): 738-743. doi: 10.1016/j.nucengdes.2009.12.015
[8]	QUADAKKERS W J, SCHUSTER H. Thermodynamic and kinetic aspects of the corrosion of high-temperature alloys in high-temperature gas-cooled reactor helium[J]. Nuclear Technology, 1984, 66(2): 383-391. doi: 10.13182/NT84-A33441
[9]	QUADAKKERS W J, SCHUSTER H. Corrosion of high temperature alloys in the primary circuit helium of high temperature gas cooled reactors. -Part I: theoretical background[J]. Materials and Corrosion, 1985, 36(4): 141-150. doi: 10.1002/maco.19850360402
[10]	石霖. 合金热力学[M]. 北京: 机械工业出版社, 1992: 539-540.
[11]	池成忠,贺志勇,高原,等. 表面渗铬T8钢中碳迁移的热力学分析[J]. 中国表面工程,2004, 17(4): 38-41. doi: 10.3321/j.issn:1007-9289.2004.04.010
[12]	QUADAKKERS W J. Corrosion of high temperature alloys in the primary circuit helium of high temperature gas cooled reactors. Part II: Experimental Results[J]. Materials and Corrosion, 1985, 36(8): 335-347. doi: 10.1002/maco.19850360802
[13]	KURATA Y, OGAWA Y, NAKAJIMA H. Effect of carburizing helium environment on creep-behavior of Ni-base heat-resistant alloys for high-temperature gas-cooled reactors[J]. Journal of the Iron and Steel Institute of Japan, 1988, 74(11): 2185-2192. doi: 10.2355/tetsutohagane1955.74.11_2185
[14]	KURATA Y, OGAWA Y, NAKAJIMA H. Effect of decarburizing helium environment on creep behavior of Ni-base heat-resistant alloys for high-temperature gas-cooled reactors[J]. Journal of the Iron and Steel Institute of Japan, 1988, 74(2): 380-387. doi: 10.2355/tetsutohagane1955.74.2_380
[15]	HAMAMOTO S, SAKABA N, TAKEDA Y. Control method of purification system of helium coolant for suppressing decarburization of heat-resistant alloy used in very high temperature gas cooling reactors[J]. Transactions of the Atomic Energy Society of Japan, 2010, 9(2): 174-182. doi: 10.3327/taesj.J08.058
[16]	GOSSÉ S, ALPETTAZ T, CHATAIN S, et al. Chromium activity measurements in nickel based alloys for very high temperature reactors: Inconel 617, Haynes 230, and Model alloys[J]. Journal of Engineering for Gas Turbines and Power, 2009, 131(6): 062901. doi: 10.1115/1.3094017
[17]	HILPERT K, ALI-KHAN I. Mass spectrometric studies of alloys proposed for high-temperature reactor systems: I. Alloy in-643[J]. Journal of Nuclear Materials, 1978, 78(2): 265-271. doi: 10.1016/0022-3115(78)90447-6
[18]	HILPERT K, GERADS H, LUPTON D F. Mass spectrometric studies of alloys proposed for high temperature reactor systems: II. Inconel alloy 617 and Nimonic alloy PE 13[J]. Journal of Nuclear Materials, 1979, 80(1): 126-131. doi: 10.1016/0022-3115(79)90228-9
[19]	GOSSÉ S, ALPETTAZ T, ROUILLARD F, et al. Direct measurements of the chromium activity in complex nickel base alloys by high temperature mass spectrometry[J]. Materials Science Forum, 2008, 595-598: 975-985. doi: 10.4028/www.scientific.net/MSF.595-598.975