Design and Optimization of Typical Cells of Solid Core for Heat Pipe Reactor
-
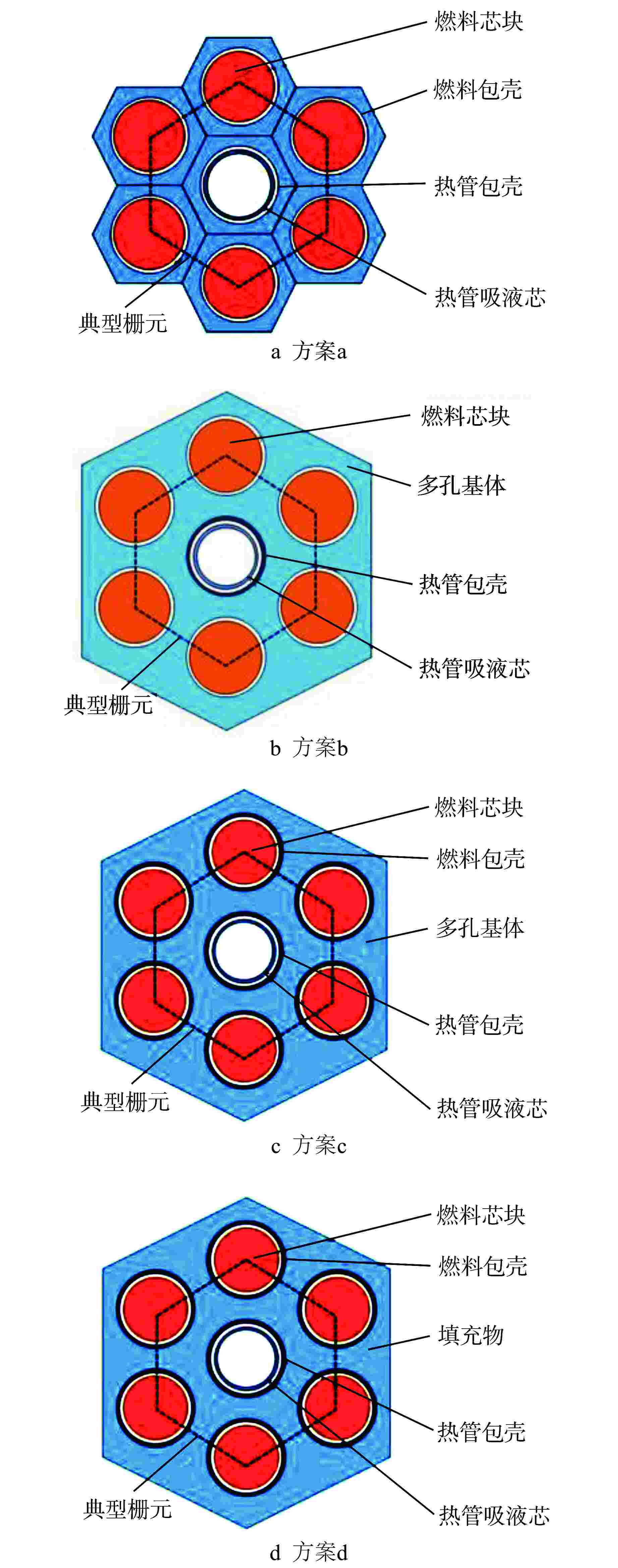
摘要: 热管堆固态堆芯设计是影响堆芯传热性能和结构完整性的关键问题。为避免固态堆芯设计中间隙热阻导致的温度和应力过大，本文建立了四种堆芯典型栅元的三维热力学模型，对不同填充物下间隙尺寸和栅元截面尺寸等关键参数进行了优化分析。结果表明，尽管高热导率的液态钠填充装配间隙能够有效降低燃料包壳和芯块温度，但热应力反而可能增大；圆管插入液态钠方案的热力学性能最优；固态堆芯方案中，六角管拼接氦气填充方案的热力学性能最优。Abstract: The solid reactor core design is a key problem in heat pipe reactor, which can affect the reactor heat transfer performance and structural integrity. To avoid the over high temperature and excessive stress caused by the gap thermal resistance, the three-dimensional thermodynamics models for typical cells of four reactor core designs have been established for optimal calculation with different fillings under the key parameters about gap size and cell section size. The result showed that, the fuel cladding and pellet temperature decrease effectively with filling the assembly clearance with liquid sodium which has high thermal conductivity, but the thermal stress increases instead. The thermodynamic performance of tubes with liquid sodium is the best; Among the solid core solutions, the thermodynamic performance of hexagonal tubes filling with helium is best in solid reactor core designs.
-
Key words:
- Solid reactor core /
- Heat pipe /
- Fuel element /
- Thermal-Mechanical coupling /
- Optimization analysis
-
图 1 4种堆芯典型栅元示意图
Figure 1. Schematic Diagram of Typical Cells of Four Reactor Core Designs
图 3 AISI 316不锈钢的屈服强度与温度关系
Figure 3. Relationship between the Yield Strength and Temperature of AISI 316 Stainless Steel
图 5 方案d最大第一主应力和温度计算结果
Figure 5. Calculated Results of Maximum First Main Stress and Temperature of Method d
表 1 输入参数
Table 1. Input Parameters
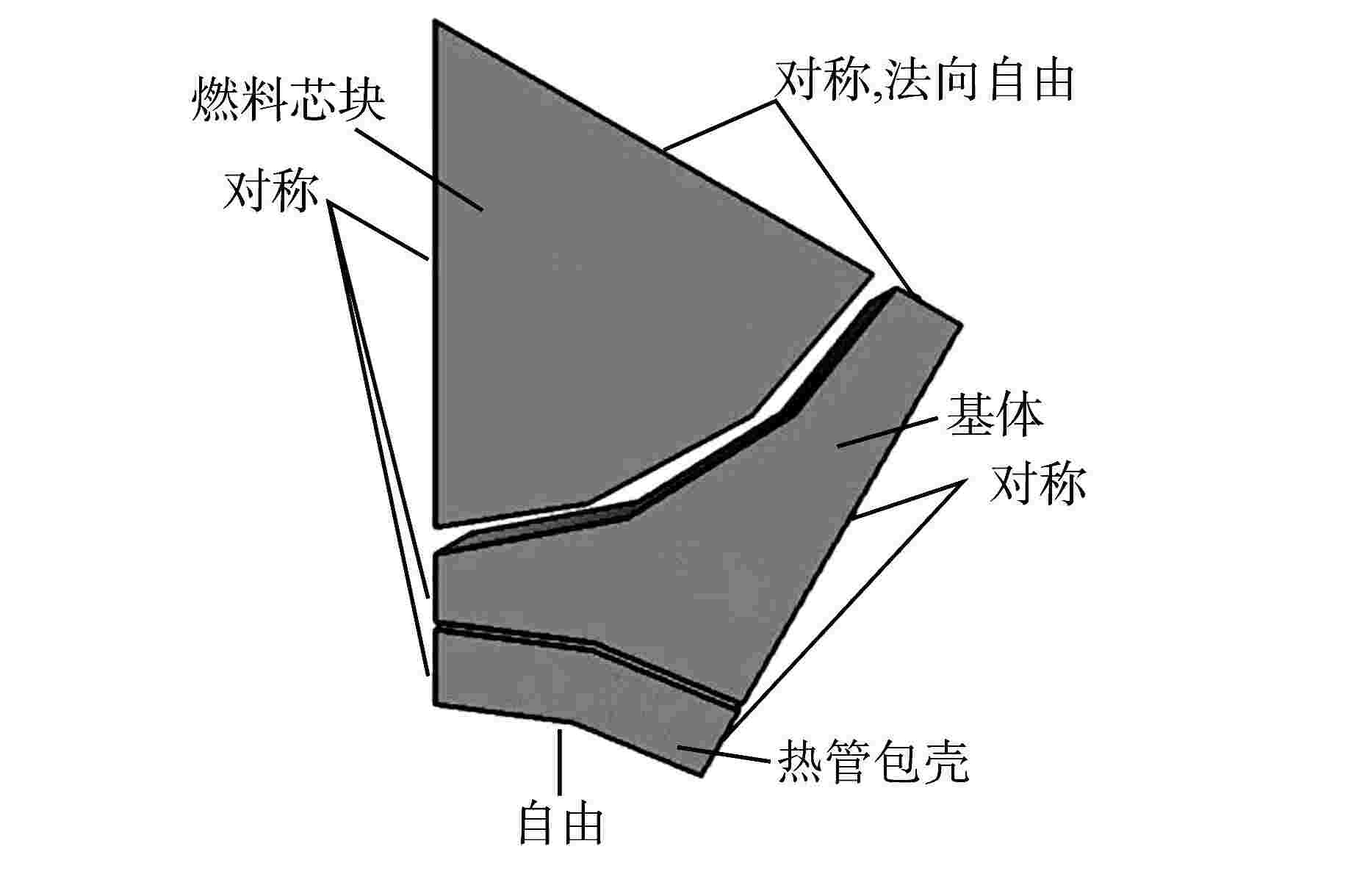
燃料棒最大线功率密度/（kW·m−1） 4.08 燃料芯块直径/mm 14.12 燃料包壳内径（r1）/mm 14.185 燃料包壳外径（r2）/mm 15.185 热管壁厚/mm 1 热管外径（r3）/mm 15.185 热管内壁面温度/℃ 675 活性区高度/mm 1500 
下载: 导出CSV
表 2 优化变量
Table 2. Optimization Variables
方案 r2/mm 装配间隙/mm r3/mm 基体厚度/mm a 15.185~16.185 0.1~0.3 r2 — b — 0.1~0.3 15.185 1~2 c 15.185~16.185 0.1~0.3 r2 1~2 d 15.185~16.185 0 r2 0.1~2 “—”表示无此项
下载: 导出CSV
表 3 典型栅元设计优化结果
Table 3. Optimization Results of Typical Cell Design
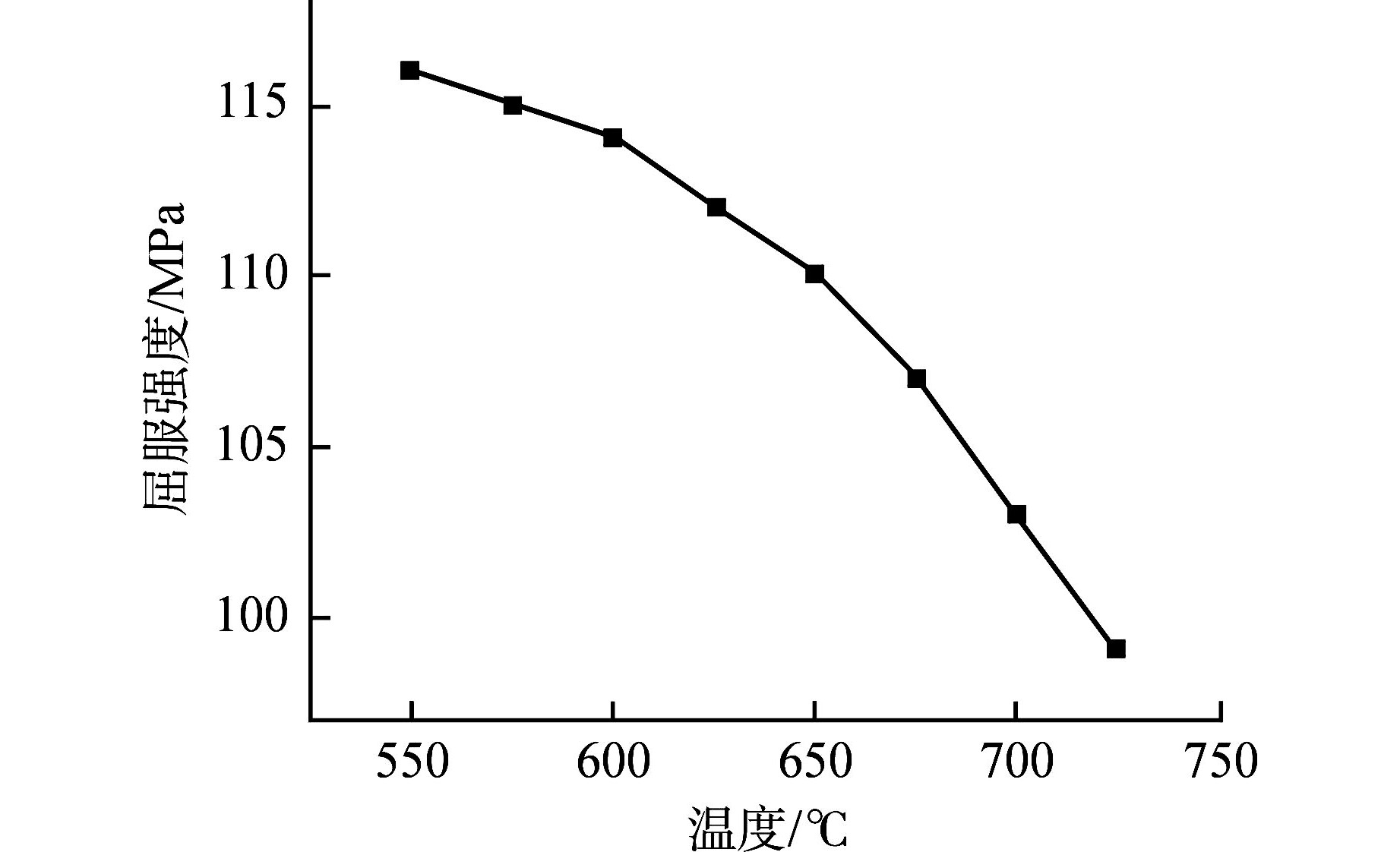
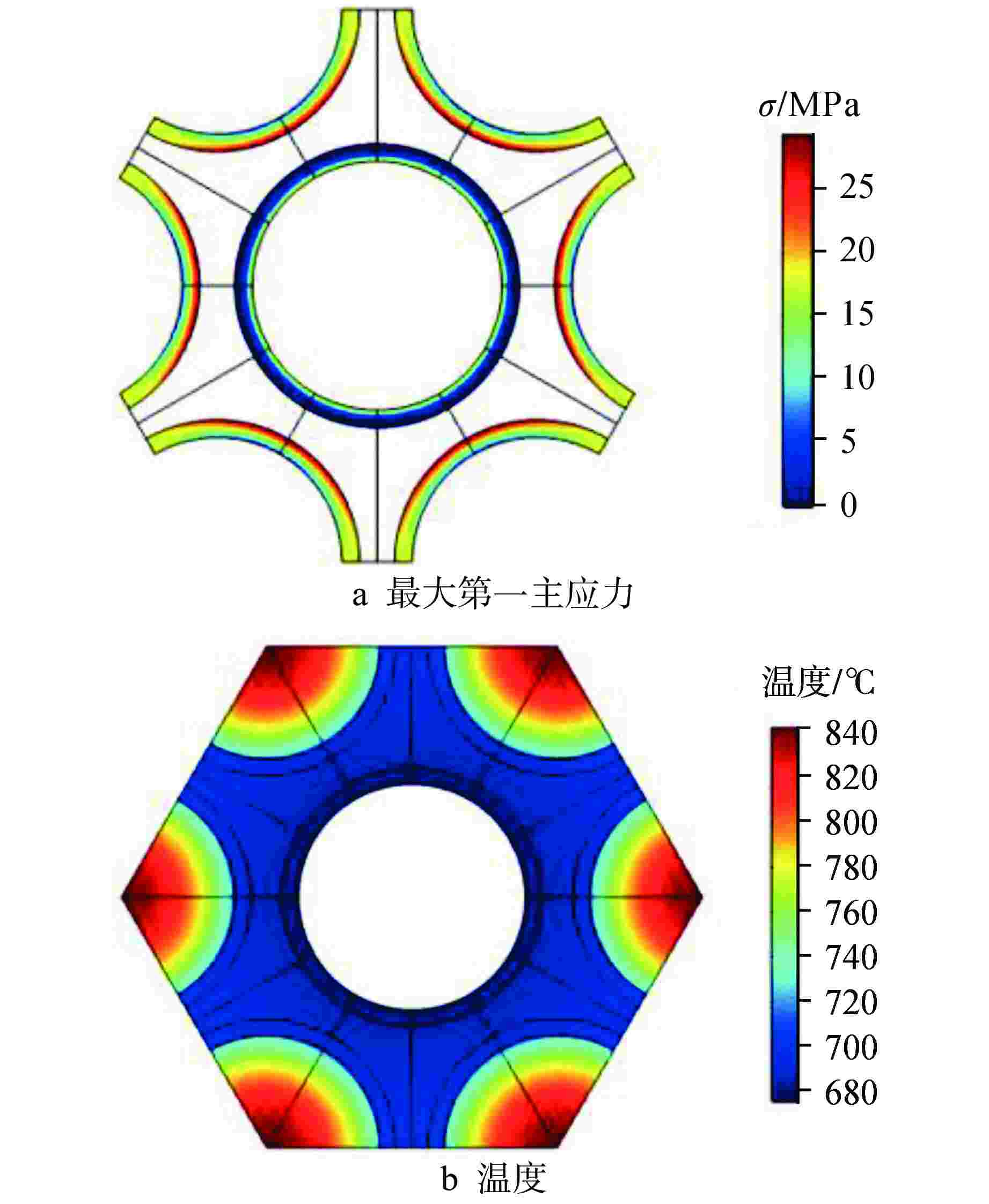
方案 优化变量 芯块 包壳/基体结构 a 填充物 燃料包壳外径/mm 装配间隙/mm 最高温度/℃ σ/MPa 最高温度/℃ σ0.2/MPa σ/σ0.2 氦气 16.185 0.10 910 45.2 779 90.36 0.50 液态钠 16.185 0.18 851 68.1 723 99.32 0.69 氟化盐 16.185 0.24 897 46.0 767 92.28 0.50 b 填充物 基体厚度/mm 装配间隙/mm 最高温度/℃ σ/MPa 最高温度/℃ σ0.2
/MPaσ/σ0.2 氦气 2.00 0.15 951 42.2 815 84.62 0.50 液态钠 1.19 0.30 854 70.7 726 98.79 0.72 氟化盐 1.81 0.30 919 45.6 785 89.48 0.51 c 填充物 燃料包壳外径/mm 装配间隙/mm 基体厚度/mm 最高温度/℃ σ/MPa 最高温度/℃ σ0.2
/MPaσ/σ0.2 氦气 16.185 0.10 2.00 949 50.7 805 86.20 0.59 液态钠 16.077 0.23 1.39 857 77.1 724 99.16 0.78 氟化盐 16.120 0.10 1.62 889 62.9 752 94.68 0.66 d 填充物 燃料包壳外径/mm 填充间隙/mm 最高温度/℃ σ/MPa 最高温度/℃ σ0.2
/MPaσ/σ0.2 液态钠 16.185 2.00 843 29.5 705 102.26 0.29
下载: 导出CSV
-
[1] POSTON D I, KAPERNICK R J, GUFFEE R M. Design and analysis of the SAFE-400 space fission reactor[J]. AIP Conference Proceedings, 2002, 608(1): 578-608. [2] RAGHEB M. Nuclear, plasma and radiation science. Chapter2: space power reactors[R]. USA: University of Illinois at Urbana-Champaign, 2016 [3] POSTON D I, KAPERNICK R J, GUFFEE R M, et al. Design of a heatpipe-cooled Mars-surface fission reactor[J]. AIP Conference Proceedings, 2002, 608(1): 1096-1106. [4] MCCLURE P R, POSTON D I, DASARI R V, et al. Design of Megawatt power level heat pipe reactors[R]. Los Alamos: Los Alamos National Laboratory, 2015. [5] STERBENTZ J W, WERNER J E, HUMMEL A J, et al. Preliminary assessment of two alternative core design concepts for the special purpose reactor[R]. USA: Idaho National Laboratory, 2018 [6] MATTHEWS C, WILKERSON R B, JOHNS R C, et al. Task 1: evaluation of M&S tools for micro-reactor concepts[R]. Los Alamos: Los Alamos National Laboratory, 2019. [7] KAPERNICK R J, GUFFEE R M. Thermal stress calculations for heatpipe-cooled reactor power systems[J]. AIP Conference Proceedings, 2003, 654(1): 457-465. [8] STERBENTZ J W, WERNER J E, MCKELLAR M G, et al. Special purpose nuclear reactor (5MW) for reliable power at remote sites assessment report[R]. USA: Idaho National Laboratory, 2017 [9] 胡攀,陈立新,王立鹏,等. 热管冷却反应堆燃料组件稳态热分析[J]. 现代应用物理,2013, 4(4): 374-378. doi: 10.3969/j.issn.2095-6223.2013.04.014 [10] 孙浩, 王成龙, 刘逍, 等. 水下航行器微型核电源堆芯初步设计[C]//第十五届全国反应堆热工流体学术会议暨中核核反应堆热工水力技术重点实验室学术年会论文集. 荣成: 中国核学会, 2017. [11] 路怀玉, 唐昌兵, 李垣明, 等. 热管反应堆燃料元件的堆内行为演化模拟研究[J]. 核动力工程, 2019, 40(S2): 82-87. [12] SCDAP/RELAP5-3D Code Development Team. SCDAP/RELAP5-3D code manual[R]. USA: Idaho National Engineering and Environmental Laboratory, 2003. [13] ASME锅炉及压力容器委员会材料分委会. ASME锅炉及压力容器规范国际性规范: Ⅱ 材料D篇 性能(公制)[M]. 中石协ASME规范产品专业委员会, 译. 北京: 中国石化出版社, 2010: 730-746. [14] 许义军. 快堆热工流体力学[M]. 北京: 中国原子能出版传媒有限公司, 2011: 53-57. [15] 长谷川正义, 三岛良绩. 核反应堆材料手册[M]. 孙守仁, 译. 北京: 中国原子能出版社, 1987: 459-461. [16] 丁能根. 汽车主动控制系统中参数估计的方法与应用[M]. 北京: 北京航空航天大学出版社, 2013: 61-65. -
计量
- 文章访问数: 322
- HTML全文浏览量: 98
- PDF下载量: 56
- 被引次数: 0
