Fatigue Reliability Evaluation Method for Hold Down Spring of Reactor Vessel Internals Considering Stress Relaxation and Irradiation
-
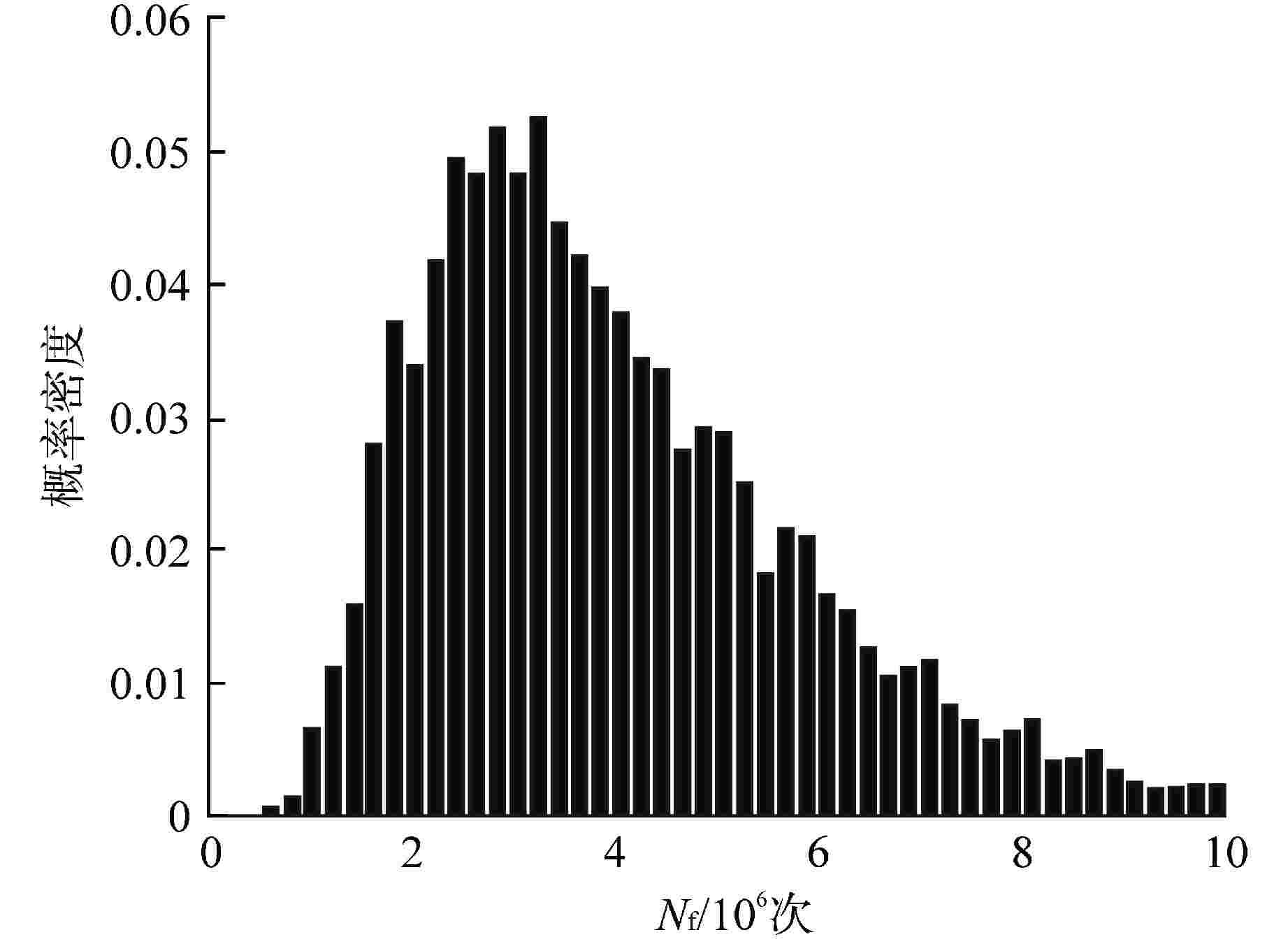
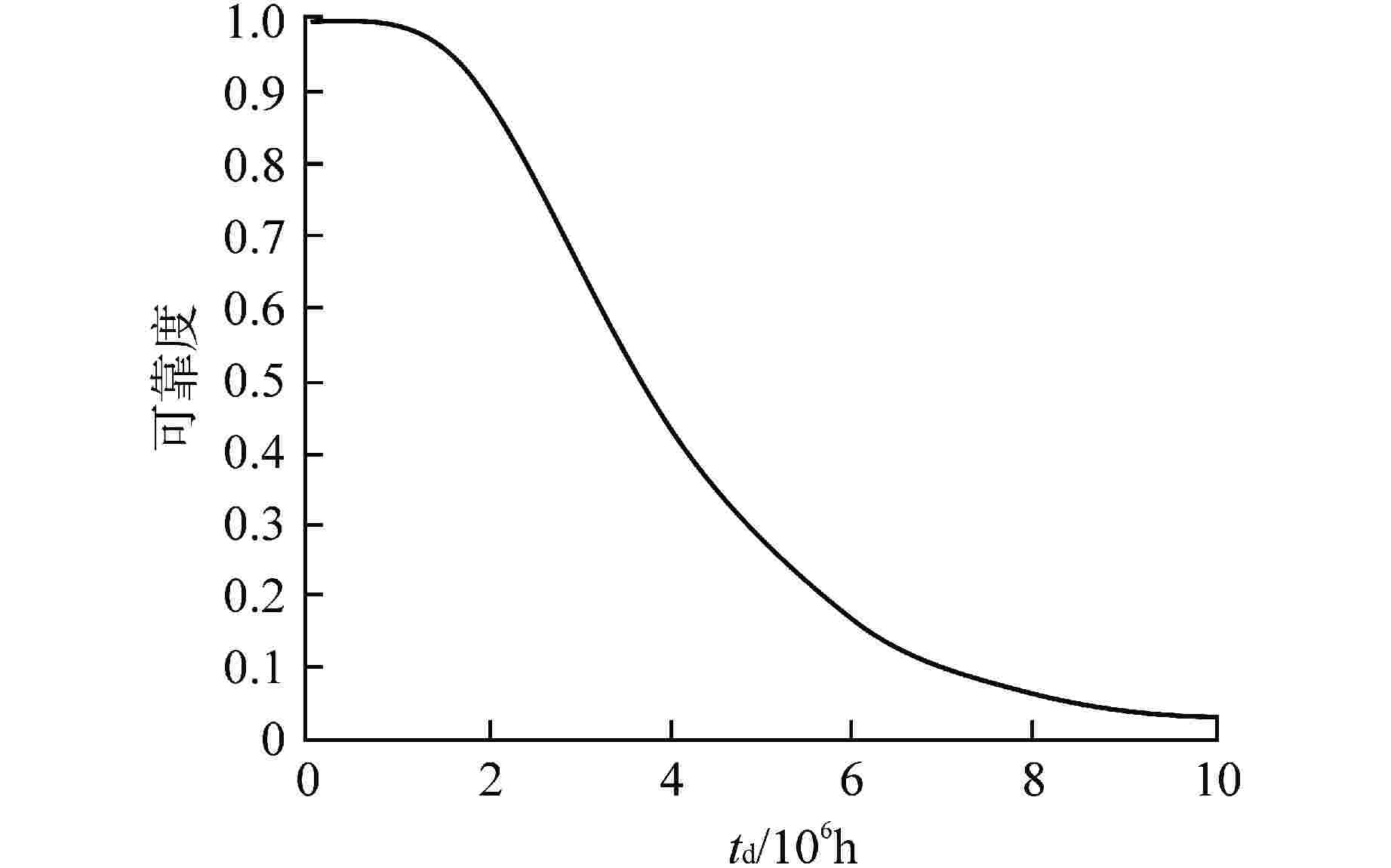
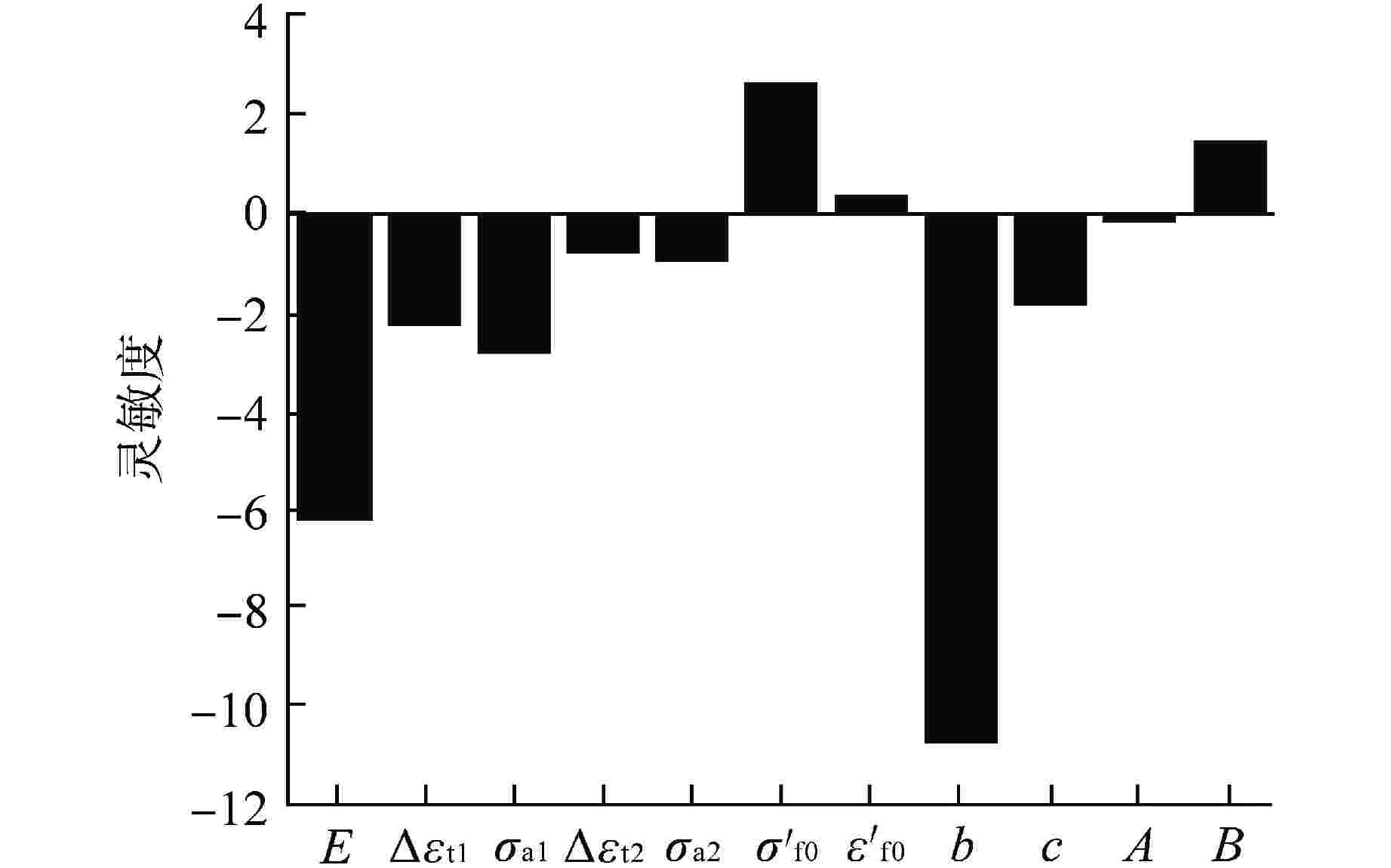
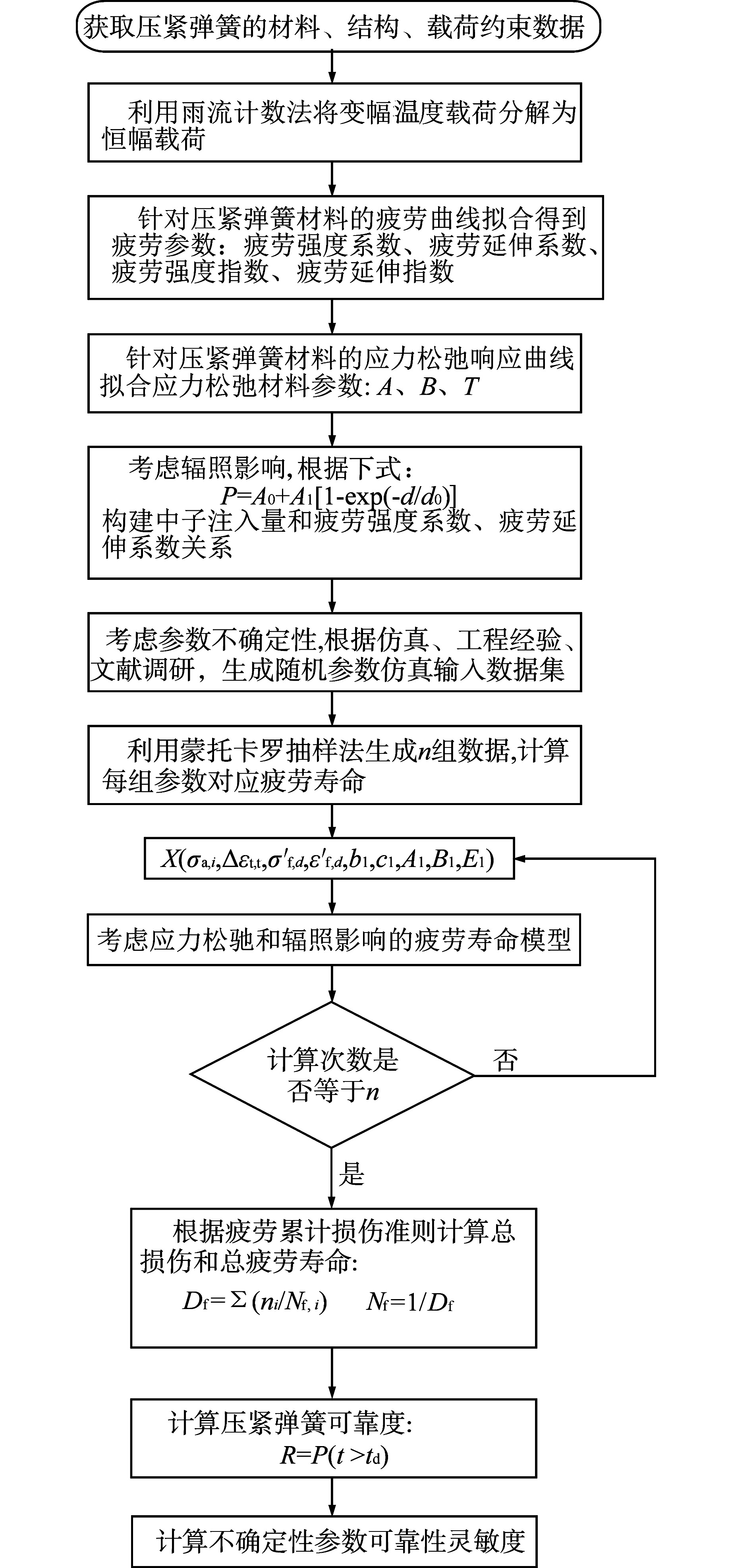
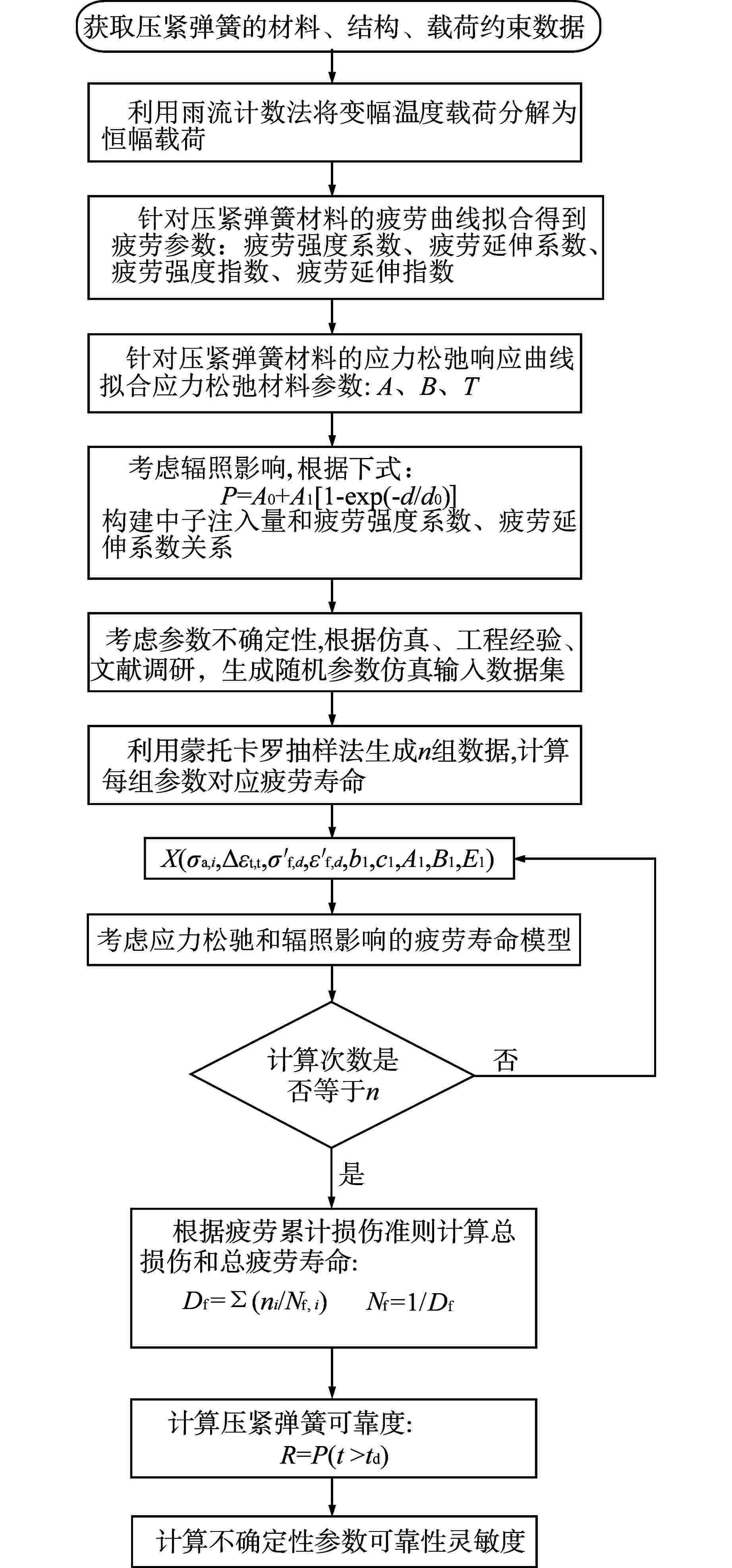
摘要: 针对反应堆堆内构件压紧弹簧疲劳失效模式，在考虑应力松弛和辐照影响的条件下基于仿真方法开展可靠性评估。首先结合疲劳模型和平均应力松弛Landgraf模型，考虑辐照对疲劳参数的影响，构建了压紧弹簧疲劳寿命模型。在压紧弹簧疲劳寿命模型基础上，根据广义应力-强度干涉模型定义压紧弹簧可靠度并开展灵敏度分析。以非能动压水堆AP1000压紧弹簧为例进行案例分析，在95%置信度水平下，分别计算了可靠度为95%和50%时对应的疲劳寿命。结果表明，若不考虑应力松弛，压紧弹簧总疲劳寿命下降88.3%；从经济性角度考虑寿命预测结果较为保守。通过灵敏度分析发现对可靠度影响较大的设计变量是弹性模量和疲劳强度系数，在一定可靠度下可以通过调整设计变量对压紧弹簧的疲劳可靠性评估进行优化。Abstract: For the fatigue failure modes of the holddown spring of reactor internals, the reliability evaluation was carried out based on the simulation method under the condition of considering the stress relaxation and the influence of radiation. Firstly, combining the fatigue model and the stress relaxation Landgraf model, considering the influence of irradiation on the fatigue parameters, the fatigue life model of the holddown spring was established. Based on the holddown spring fatigue life model, the reliability of holddown spring was defined according to the generalized stress-strength interference model and the sensitivity analysis was carried out. Taking the holddown spring of AP1000 passive pressurized water reactor as an example, the fatigue life with a reliability of 95% and 50% at 95% confidence level were calculated. The results show that the total fatigue life of the holddown spring decreases by 88.3% without considering the stress relaxation, and the prediction results are conservative from the perspective of economy. The results of sensitivity analysis show that the elastic modulus and fatigue strength coefficient have great influence on reliability. The holddown spring can be optimized by adjusting the design variables under certain reliability requirements.
-
Key words:
- Holddown spring /
- Reliability /
- Fatigue /
- Stress relaxation /
- Irradiation /
- Reactor structure
-
图 1 压紧弹簧疲劳可靠性评估方法流程
Figure 1. Process of Fatigue Reliability Evaluation Method for Holddown Spring
图 2 总疲劳寿命概率密度分布
Figure 2. Probability Density Distribution of the Total Fatigue Lifetime
表 1 压紧弹簧材料性能参数
Table 1. Material Performance Parameters of Holddown Spring
参数名 数值 密度/(kg·m−2) 7750 杨氏模量/ GPa 193.5 泊松比 0.3 热膨胀系数/℃−1 1.095×10−5 屈服强度/ MPa 513 抗拉强度/ MPa 687 
下载: 导出CSV
表 2 随机变量及分布特征
Table 2. Random Variables and Distribution Characteristics
参数 分布类型 均值 标准差 $ E $ 正态分布 193.5 GPa 9.675 GPa $ \Delta {\varepsilon _{{\text{t1}}}} $ 正态分布 0.16% 0.00163% $ {\sigma _{{\text{a1}}}} $ 正态分布 101.2 MPa 1.002 MPa $ \Delta {\varepsilon _{{\text{t2}}}} $ 正态分布 0.14% 0.00138% $ {\sigma _{{\text{a2}}}} $ 正态分布 95.3 MPa 0.95 MPa $ \sigma _{{\text{f0}}}^\prime $ 正态分布 1130 MPa 56.5 MPa $ \varepsilon _{{\text{f0}}}^\prime $ 正态分布 1.291 0.0646 $ b $ 正态分布 −0.12 0.0012 $ c $ 正态分布 −0.6 0.006 $ A $ 正态分布 0.026 0.0013 $ B $ 正态分布 −197.415 9.871 $ \Delta {\varepsilon _{{\text{t1}}}} $—大温度循环下应变范围；$ {\sigma _{{\text{a1}}}} $—大温度循环下应力幅；$ \Delta {\varepsilon _{{\text{t2}}}} $—小温度循环下应变范围；$ {\sigma _{{\text{a2}}}} $—小温度循环下应力幅；$ \sigma _{{\text{f0}}}^\prime $—疲劳强度系数辐照前初始值；$ \varepsilon _{{\text{f0}}}^\prime $—疲劳延伸系数辐照前初始值
下载: 导出CSV
表 3 疲劳寿命计算结果
Table 3. Fatigue Life Calculation Results
参数 可靠度 确定性计算 95% 50% 考虑应力松弛 不考虑应力松弛 ${N_{\rm{f}}}$/次 1629982 3685678 4154566 484857 ${T_{\rm{f}}}$/a 96.5 420.7 474.2 55.3
下载: 导出CSV
-
[1] SCHNEIDER M, FROGGATT A. World nuclear industry status report 2019[R]. Paris: Mycle Schneider Consulting, 2019 : 5-6. [2] 张翟,薛国宏. 压紧弹性环的设计方案优化分析[J]. 核技术,2013, 36(4): 38-42. [3] XIE L J, XUE G H, ZHANG M. Research on friction coefficient of nuclear reactor vessel internals hold down spring: stress coefficient test analysis method[J]. Nuclear Engineering and Design, 2016(304): 11-18. doi: 10.1016/j.nucengdes.2016.04.023 [4] XIE L J, XUE G H, ZHANG M. Evolution law of the friction coefficient and fatigue test of the hold-down spring model for nuclear reactor vessel internals[J]. Progress in Nuclear Energy, 2018(105): 160-166. doi: 10.1016/j.pnucene.2018.01.008 [5] 高靖云,张成成,侯乃先,等. 考虑应力松弛的单晶涡轮叶片蠕变疲劳寿命预测[J]. 航空动力学报,2016, 31(3): 539-547. [6] MANSON S S, HIRSCHBERG M H. Fatigue: an interdisciplinary approach[M]. Syracuse: Syracuse University Press, 1964: 361-373. [7] 覃鹏,王国辉. 基于有限元分析的涡轮盘疲劳寿命预测[J]. 兵器装备工程学报,2018, 39(8): 176-178. doi: 10.11809/bqzbgcxb2018.08.037 [8] SMITH R N, WATSON P, TOPPER T H. A stress-strain function for the fatigue of metals[J]. Journal of Materials, 1970, 5(4): 767-778. [9] CHOPRA O K, RAO A S. A review of irradiation effects on LWR core internal materials – IASCC susceptibility and crack growth rates of austenitic stainless steels[J]. Journal of Nuclear Materials, 2011, 409(3): 235-256. doi: 10.1016/j.jnucmat.2010.12.001 [10] 郭进全,轩福贞,王正东,等. 基于蠕变的高温构件应力松弛损伤模型[J]. 核动力工程,2009, 30(4): 9-12. [11] 张孝忠,王恭义,程凯,等. 一种考虑平均应力松弛的汽轮机叶根低周疲劳寿命预测方法[J]. 材料科学与工程学报,2019, 37(5): 709-713. [12] 陆明万,寿比南,杨国义. 疲劳分析中变幅载荷的循环计数方法[J]. 压力容器,2012, 29(11): 25-29+6. doi: 10.3969/j.issn.1001-4837.2012.11.005 [13] DIRECTIVE P E. ASME boiler and pressure vessel code 2015 edition Ⅷ: rules for construction of pressure vessels[S]. New York: American Society of Mechanical Engineers, 2015: 97-98. [14] LANDGRAF R W, CHERNENKOFF R A. Residual stress effects on fatigue of surface processed steels[C]. Philadelphia: American Society for Testing and Materials, 1988: 105-106. [15] 张义民. 机械可靠性漫谈[M]. 北京: 科学出版社, 2012: 90-91. [16] 王庆田,罗英,胡朝威,等. 压水堆核电厂堆内构件结构材料优化选择[J]. 中国核电,2016, 9(4): 298-305. [17] DIRECTIVE P E. ASME Boiler and pressure vessel code 2015 edition Ⅲ: rules for construction of nuclear facility components[S]. New York: American Society of Mechanical Engineers, 2015 :52-53. -
图(4) / 表(3)
计量
- 文章访问数: 207
- HTML全文浏览量: 104
- PDF下载量: 37
- 被引次数: 0
