Research on Verification Methodology of Applicability of Integral Effect Test Data Based on Dimensionless Criterion Numbers
-
摘要: 在进行核反应堆与核动力装置安全性评估的过程中,一般需要基于相似比例法则建立整体效应试验(IET)或分离效应实验(SET)台架,为安全性能验证与评估提供数据支撑。作为衡量比例相似程度的重要参数,无量纲准则数可以对特定物理现象做出独立于台架特性、装置尺寸等的表征,因此可以用于比例设计的合理性验证以及实验数据的适用性评估。对无量纲数的跨台架应用可以避免过量重复性实验,也可辅助评估单一台架未能准确复现的某个物理现象。为了探索无量纲数在比例分析和实验数据适用性评估中的应用方法和原则,本文针对传统压水堆的小破口失水事故(SBLOCA),基于RELAP5数值模拟结果,使用自上而下的比例分析方法对整体效应试验台架LOFT和LOBI进行无量纲参数计算和数据对比。分析结果表明,与破口质量流出、堆芯衰变热、一回路压力等重要现象和参数相关的无量纲数跨台架吻合较好;而与回路摩擦阻力、回路浮升力等相关的无量纲数比率有较大失真。本文采用的无量纲分析方法预期可用于同类型试验台架的实验数据互验,并为新堆型的开发和验证提供参考。Abstract: In the process of evaluating the safety of nuclear reactors and nuclear power plants, it is generally necessary to establish integral effect test or separate effect test bench based on the similar scaling laws to provide data support for safety performance verification and evaluation. As important parameters to measure the degree of similarity of scaling, dimensionless criterion numbers can characterize specific physical phenomena independent of the bench characteristics and the device size. Therefore, they can be used to verify the rationality of scaling design and evaluate the applicability of experimental data. The cross-bench application of dimensionless numbers can not only avoid excessive repetitive experiments, but also assist in the evaluation of a physical phenomenon that can not be accurately reproduced by a single bench. In order to explore the application methods and principles of dimensionless numbers in scaling analysis and applicability evaluation of experimental data, in this paper, aiming at SBLOCA of the traditional PWR, based on the numerical simulation results of RELAP5, the top-down scaling analysis method is used to calculate the dimensionless parameters and compare the data of the integral effect test bench LOFT and LOBI. The analysis results show that the dimensionless numbers related to important phenomena and parameters such as break mass outflow, core decay heat and primary circuit pressure are in good agreement with the bench; the dimensionless number ratios related to loop friction resistance and loop buoyancy have great distortion. The dimensionless analysis method used in this paper is expected to be used for mutual verification of experimental data on the same type of test bench, and to provide a reference for the development and verification of new reactor types.
-
图 3 饱和场和过冷场流域划分原理图[6]
Figure 3. Schematic Diagram of Flow Field Division of Saturation Field and Supercooling Field
图 4 单饱和场流域划分原理图[6]
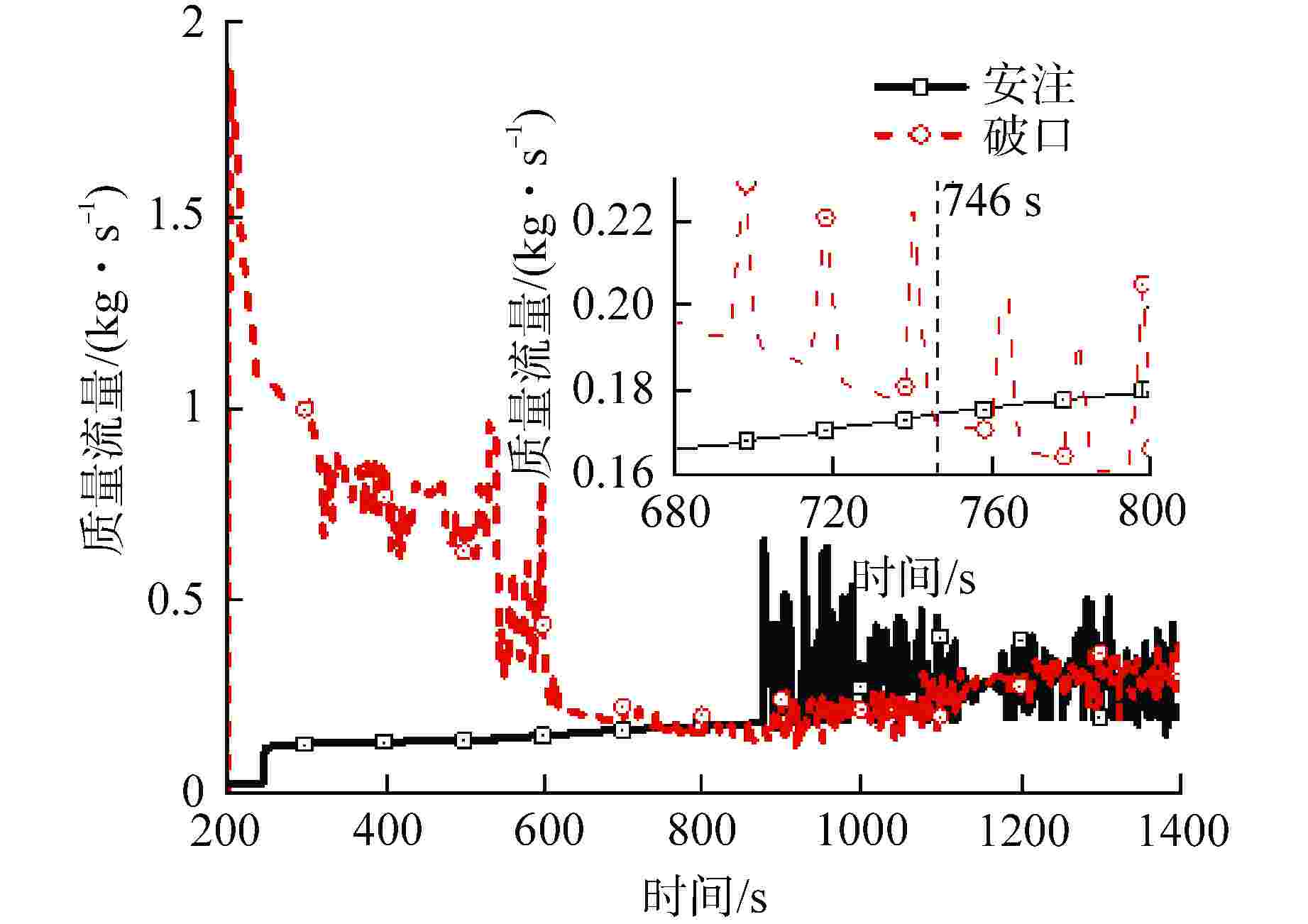
$\dot{Q}_{\rm{net}} $—系统净吸热量,$\dot{m}_{\rm{break}} $—通过破口流失的质量流量
Figure 4. Schematic Diagram of Flow Field of Single Saturation Field
表 1 LOFT和LOBI初始条件
Table 1. Initial Conditions of LOFT and LOBI
初始条件参数 LOFT LOBI 功率/MW 49±1 5.28 一回路压力/MPa 14.86±0.14 15.8 冷管段温度/K 558±1 567.15 破口大小/% ~1 3 表 2 LOFT和LOBI比例因子对比
Table 2. Comparison of Scaling Factors of LOFT and LOBI
参数(台架/原型堆) LOFT LOBI 总功率比 0.013 0.001 总水装量比 0.02 0.002 高度比 0.5 1 压力比 0.969 0.969 环路数比 0.5 0.5 功率/体积比 0.6 0.6 时间比 1 1 参数 表达式 物理意义 ${M^ * }$ $ {M / {{M_0}}} $ 无量纲质量 ${t^*}$ ${t / {{t_0}}}$ 无量纲时间 $\dot m_{{\text{break}}}^{\text{*}}$ ${\dot m_{{\text{break}}}}/{\dot m_{{\text{break,0}}}}$ 无量纲质量流量 ${P^{\text{*}}}$ $ {P / {{P_0}}} $ 无量纲压力 $I_{{\text{b,l}}}^{\text{*}}$ ${{{I_{{\text{b,l}}}}} / {{I_{{\text{b,l,0}}}}}} = {{{{\dot m}_{{\text{break}}}}({h_{{\text{out}}}} - {u_{\text{l}}})} / {{{\dot m}_{{\text{break,0}}}}{{({h_{{\text{out}}}} - {u_{\text{l}}})}_0}}}$ 质量外流引起无量纲液体能量变化 $I_{{\text{c,m}}}^{\text{*}}$ ${{{I_{{\text{c,m}}}}} / {{I_{{\text{c,m,0}}}}}} = {{{{\dot q}_{{\text{net,m}}}}} / {{{\dot q}_{{\text{net,m,0}}}}}}$ 无量纲传热率 $II_{\text{l}}^{\text{*}}$ $ {{I{I_{\text{l}}}} / {I{I_{{\text{l,0}}}}}} = {{{v_{\text{l}}}\left( { - {{\dot m}_{{\text{break}}}}} \right)} / {{v_{{\text{l,0}}}}\left( { - {{\dot m}_{{\text{break}},0}}} \right)}} $ 质量外流引起无量纲液体体积变化 表 4 水封清除阶段静压液位 m
Table 4. Static Pressure Level in Seal Clearing Phase
液位 含义说明 LOFT L3-5 LOBI BL-02 LCUP,0 堆芯坍塌液位参考值 3.3843031 4.1129603 LDC,0 下降通道液位参考值 4.588439 5.9365168 LSGU,0 SG上升段液位参考值 8.8605458×10−1 1.8020197 LLCU,0 过渡段到冷段水封液位参考值 1.3761617×10−4 3.0225303×10−5 LSGD,0+LLSD,0 SG下降段及过渡段水封下降段液位之和参考值 5.6662928×10−2 7.3722704×10−2 LCUP,min 堆芯最低水位 3.0335832 2.8287368 表 5 各阶段无量纲数的量化结果
Table 5. Quantitative Results of Dimensionless Numbers at Each Stage
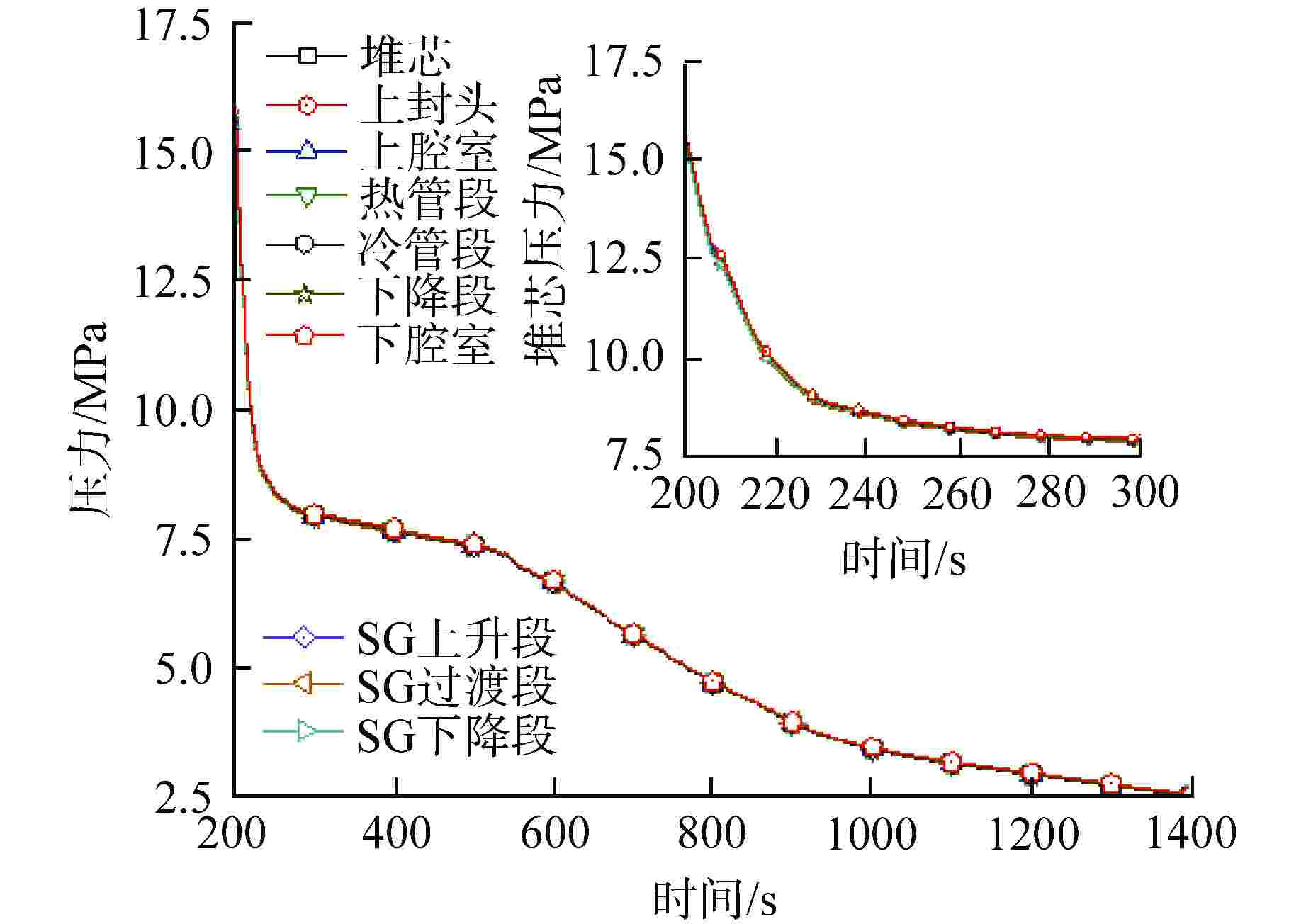
事故进程 无量纲数 表达式 含义说明 LOFT L3-5 LOBI BL-02 πR 喷放阶段 Ψ2 $\dfrac{{{C_{{\text{1,l,0}}}}\left( {{h_{{\text{break}}}} - {u_{\text{l}}}} \right){{\dot m}_{{\text{break}},0}}{t_0}}}{{{P_0}}}$ 质量外流引起过冷场的压力变化量占基准压力的比 −3.928×10−1 −5.938×10−1 0.66 Ψ6 $\dfrac{{{C_{{\text{1,m,0}}}}{{\dot q}_{{\text{net,}}0}}{t_0}}}{{{P_0}}}$ 饱和场内热源引起的压力变化量占参考压力的比 4.624×10−1 2.444×10−1 1.89 Ψ10 $\dfrac{{{C_{2,0}}{v_{{\text{l,0}}}}{{\dot m}_{{\text{break,0}}}}{t_0}}}{{{P_0}}}$ 破口外流导致比体积变化造成压力变化与参考压力的比 −4.345×10−2 −7.194×10−2 0.60 Ψ13 $\dfrac{{{{\dot m}_{{\text{break}},0}}{t_0}}}{{{M_0}}}$ 破口质量流量与参考质量流量之比 1.576×10−1 2.566×10−1 0.61 自然循环阶段 Ψ5 $\dfrac{{{C_{{\text{1,m,0}}}}({h_{{\text{out}}}} - {u_{\text{m}}}){{\dot m}_{{\text{break,0}}}}{t_0}}}{{{P_0}}}$ 质量外流引起饱和场的压力变化量占基准压力的比 −1.352 −1.407 0.96 Ψ6 $\dfrac{{{C_{1,m,0}}{{\dot q}_{{\text{net,0}}}}{t_0}}}{{{P_0}}}$ 饱和场内热源引起的压力变化量占参考压力的比 1.576 8.264×10−1 1.91 Ψ11 $\dfrac{{{C_{2,{\text{m}},0}}{v_{{\text{m}},0}}{{\dot m}_{{\text{break,}}0}}{t_0}}}{{{P_0}}}$ 破口外流导致比体积变化造成压力变化与参考压力的比 −7.928×10−2 −9.681×10−2 0.82 Ψ13 $\dfrac{{{{\dot m}_{{\text{break}},0}}{t_0}}}{{{M_0}}}$ 破口质量流量与参考质量流量之比 3.773×10−1 8.252×10−1 0.46 ${N_{\vartriangle {P_0}}}$ $\dfrac{{{P_{{\rm{o}},0}} - {P_{i,0}}}}{{{P_0}}}$ 堆芯进出口压力差(环路阻力) 2.002×10−4 1.9822×10−3 0.10 ${N_{{\text{R}}i}}$ $ \dfrac{{\displaystyle \sum \nolimits_j \left( {{\rho _{_{{\text{l,sat}}}}} - {\rho _{_{{\text{m}},i}}}} \right)g{L_{i}}}}{{\dfrac{1}{2}{\rho _{_{{\text{l,0}}}}}v_{{\text{l,0}}}^{\text{2}}}} $ 自然循环回路的浮升力 4031.142 21487.665 0.19 水封清除阶段 Ψ5 同自然循环阶段(单饱和场) −6.792×10−2 −9.265×10−2 0.73 Ψ6 1.237×10−2 5.88110−3 2.10 Ψ11 −3.10810−3 −5.02310−3 0.62 Ψ13 1.717×10−2 4.235×10−2 0.41 Π1 $\dfrac{{{L_{{\text{DC,0}}}}}}{{{L_{{\text{CUP,0}}}}}}$ 下降通道液位/堆芯坍塌液位的静压液位 1.356 1.443 0.94 Π2 $\dfrac{{{L_{{\text{SGU,0}}}}}}{{{L_{{\text{CUP,0}}}}}}$ SG上升段液位与堆芯坍塌液位的静压液位比 2.618×10−1 4.381×10−1 0.60 Π3 $\dfrac{{{L_{{\text{LSU,0}}}}}}{{{L_{{\text{CUP,0}}}}}}$ 过渡段到冷段水封液位与堆芯坍塌液位的静压液位比 4.066×10−5 7.349×10−6 5.53 Π7 $\dfrac{{{L_{{\text{SGD,0}}}} + {L_{{\text{LSD,0}}}}}}{{{L_{{\text{CUP,0}}}}}}$ SG下降段过渡段水封液位和与堆芯坍塌液位静压液位比 1.674×10−2 1.792×10−2 0.93 $L_{{\text{CUP,0}}}^{\text{*}}$ $\dfrac{{{L_{{\text{CUP,min}}}}}}{{{L_{{\text{CUP,0}}}}}}$ 堆芯的最低水位与堆芯坍塌液位的静压液位比 8.964×10−1 6.878×10−1 1.30 水蒸发阶段 Ψ5 同自然循环阶段(单饱和场) −4.201 −6.592×10−1 6.37 Ψ6 2.415×10−1 7.544×10−2 3.20 Ψ11 −1.797×10−1 −3.197×10−2 5.62 Ψ13 1.186 4.638×10−1 2.56 -
[1] 刘宇生,许超,谭思超,等. 整体试验台架非能动换热器的比例模化及设计[J]. 哈尔滨工程大学学报,2019, 40(3): 449-455. [2] 郝建立,陈文振,王少明. 自然循环蒸汽发生器倒U型管内倒流特性的无量纲分析[J]. 原子能科学技术,2012, 46(S1): 246-249. [3] 陈常念,韩吉田,邵莉,等. 临界热流密度流体模化广义准则数研究[J]. 原子能科学技术,2010, 44(5): 558-561. [4] 王杰,刘东,刘盈,等. 失水事故分析程序临界流模型改进及验证[J]. 核动力工程,2019, 40(1): 28-32. [5] 曾未,王杰,黄涛,等. 压水堆大破口失水事故重要现象识别及数值计算不确定性量化分析研究[J]. 核动力工程,2021, 42(1): 198-203. [6] LIAO J. System scaling analysis for modeling small break LOCA using the FULL SPECTRUM LOCA evaluation model[J]. Annals of Nuclear Energy, 2016, 87: 443-453. doi: 10.1016/j.anucene.2015.09.014 [7] 国家核安全局. 核动力厂安全分析用计算机软件开发与应用(试行): HAD102[S]. 北京: 国家核安全局, 2017: 3-55. [8] YANG J, CHOI S W, LIM J, et al. Counterpart experimental study of ISP-42 PANDA tests on PUMA facility[J]. Nuclear Engineering and Design, 2013, 258: 249-257. doi: 10.1016/j.nucengdes.2013.02.034 [9] LIU T J, LEE C H, WAY Y S. IIST and LSTF counterpart test on PWR station blackout transient[J]. Nuclear Engineering and Design, 1997, 167(3): 357-373. doi: 10.1016/S0029-5493(96)01302-7 [10] WULFF W, ROHATGI U S. System scaling for the Westinghouse AP600 pressurized water reactor and related test facilities: analysis and results: NUREG/CR-5541[R]. Washington, DC: Division of Systems Technology, Office of Nuclear Regulatory Research, U. S. Nuclear Regulatory Commission, 1998. [11] DENG C C, ZHANG X Y, YANG Y, et al. Research on scaling design and applicability evaluation of integral thermal-hydraulic test facilities: a review[J]. Annals of Nuclear Energy, 2019, 131: 273-290. doi: 10.1016/j.anucene.2019.03.042 [12] ADDABBO C, ANNUNZIATO A. The LOBI integral system test facility experimental programme[J]. Science and Technology of Nuclear Installations, 2012, 2012: 238019. [13] SCRIVEN A H. Analysis of LOBI test BLO2 (three percent cold leg break) with RELAP5 code: NUREG/IA-0036[R]. Washington: Office of Nuclear Regulatory Research, U. S. Nuclear Regulatory Commission, 1992. [14] DAO L T L, CARPENTER J M. Experiment data report for LOFT nuclear small break experiment L3-5/L3-5A: NUREG/CR-1695[R]. Unitedstates: INEL, 1980. [15] BESTION D, D'AURIA F, LIEN P, et al. Scaling in system thermal-hydraulics applications to nuclear reactor safety and design: a state-of-the-art report: NEA/CSNI/R(2016)14[R]. France: OECD, NEA, 2017. [16] BANERJEE S, ORTIZ M G, LARSON T K, et al. Scaling in the safety of next generation reactors[J]. Nuclear Engineering and Design, 1998, 186(1-2): 111-133. doi: 10.1016/S0029-5493(98)00219-2 [17] ZUBER N, ROHATGI U S, WULFF W, et al. Application of fractional scaling analysis (FSA) to loss of coolant accidents (LOCA): methodology development[J]. Nuclear Engineering and Design, 2007, 237(15-17): 1593-1607. doi: 10.1016/j.nucengdes.2007.01.017 [18] BUCKINGHAM E. On physically similar systems; illustrations of the use of dimensional equations[J]. Physical Review, 1914, 4(4): 345-376. doi: 10.1103/PhysRev.4.345 [19] FREPOLI C, OHKAWA K. Realistic LOCA evaluation methodology applied to the full spectrum of break sizes (full spectrum LOCA methodology): WCAP-16996-P[R]. U. S. : Westinghouse Electric Company, 2010. [20] NAHAVANDI A N, CASTELLANA F S, MORADKHANIAN E N. Scaling laws for modeling nuclear reactor systems[J]. Nuclear Science and Engineering, 1979, 72(1): 75-83. doi: 10.13182/NSE79-A19310 [21] REYES J. Natural circulation in water cooled nuclear power plants phenomena, models, and methodology for system reliability assessments: IAEA-TECDOC-1474[R]. Austria: Nuclear Power Technology Development Section, International Atomic Energy Agency, 2005. -





 下载:
下载: