Research on Calculation of Interfacial Resistance in One-Dimensional Two-Fluid Model
-
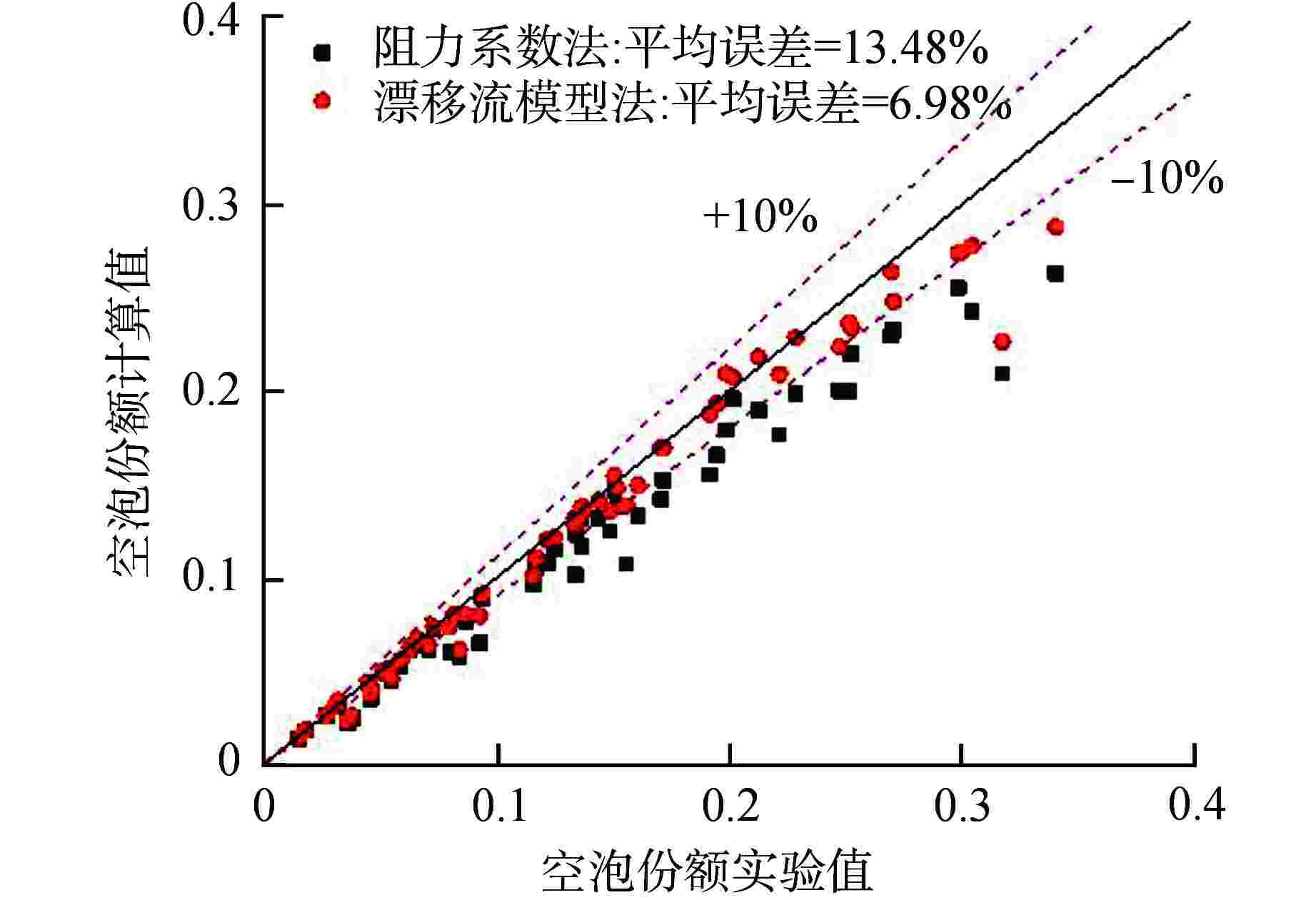
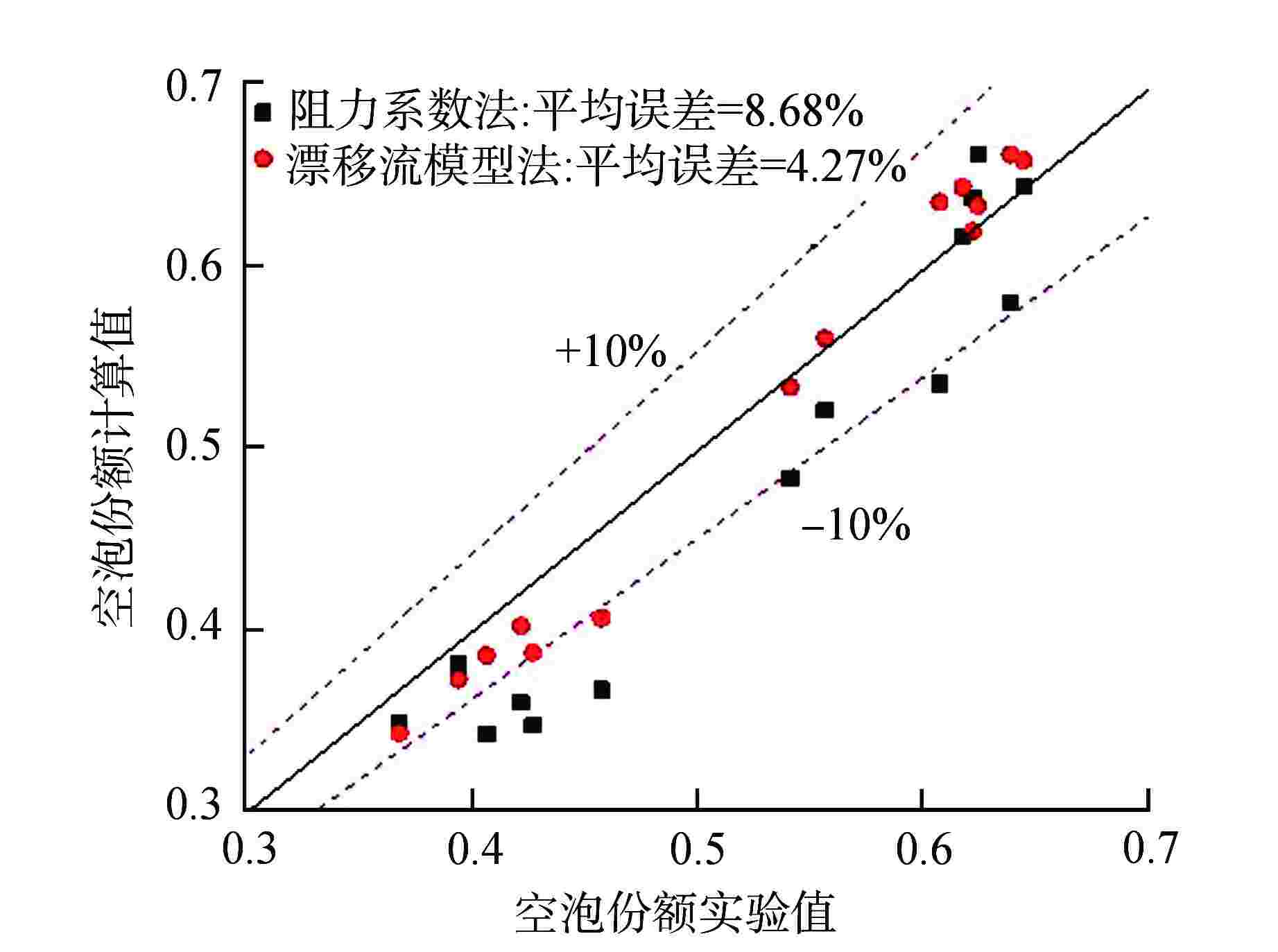
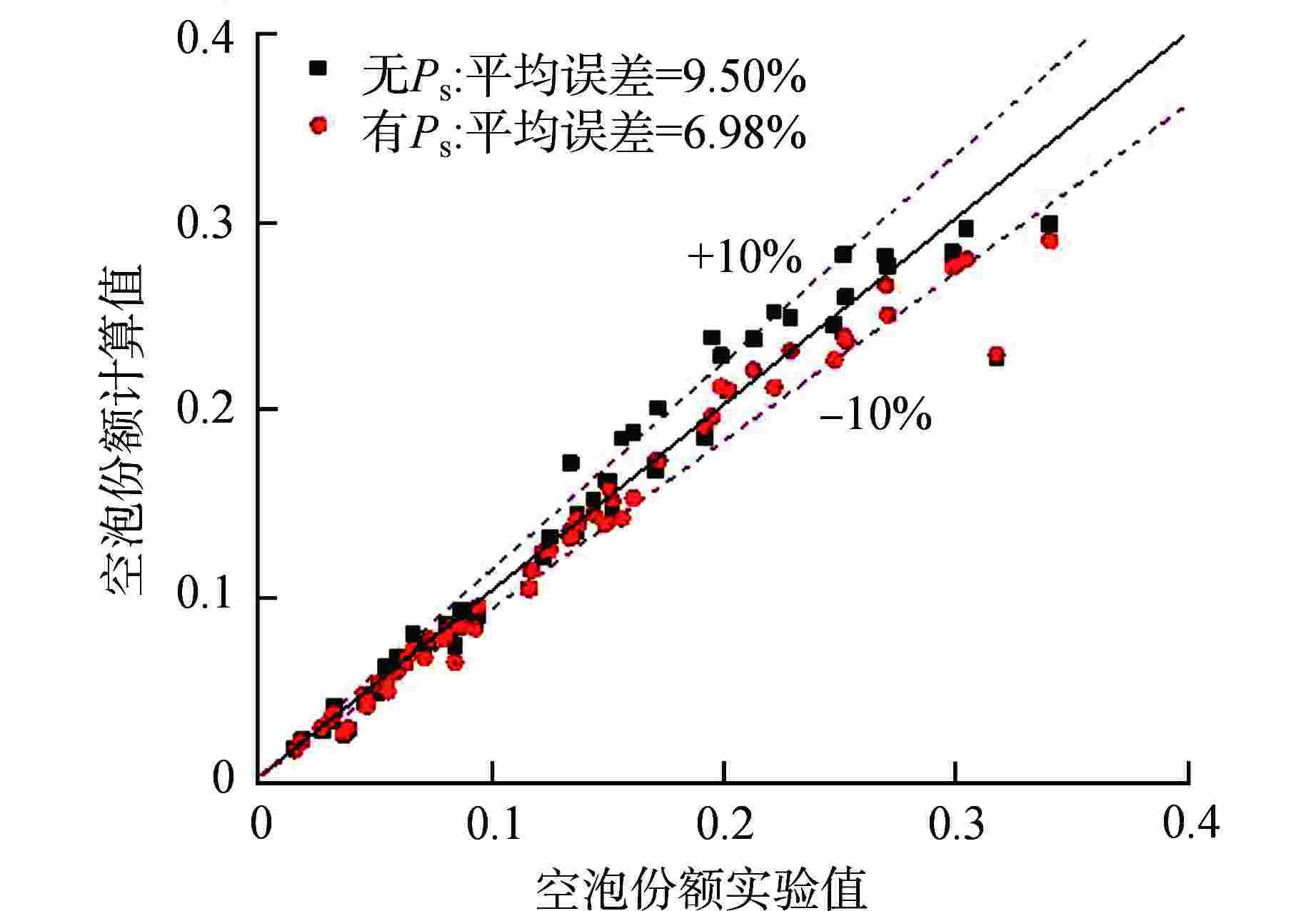
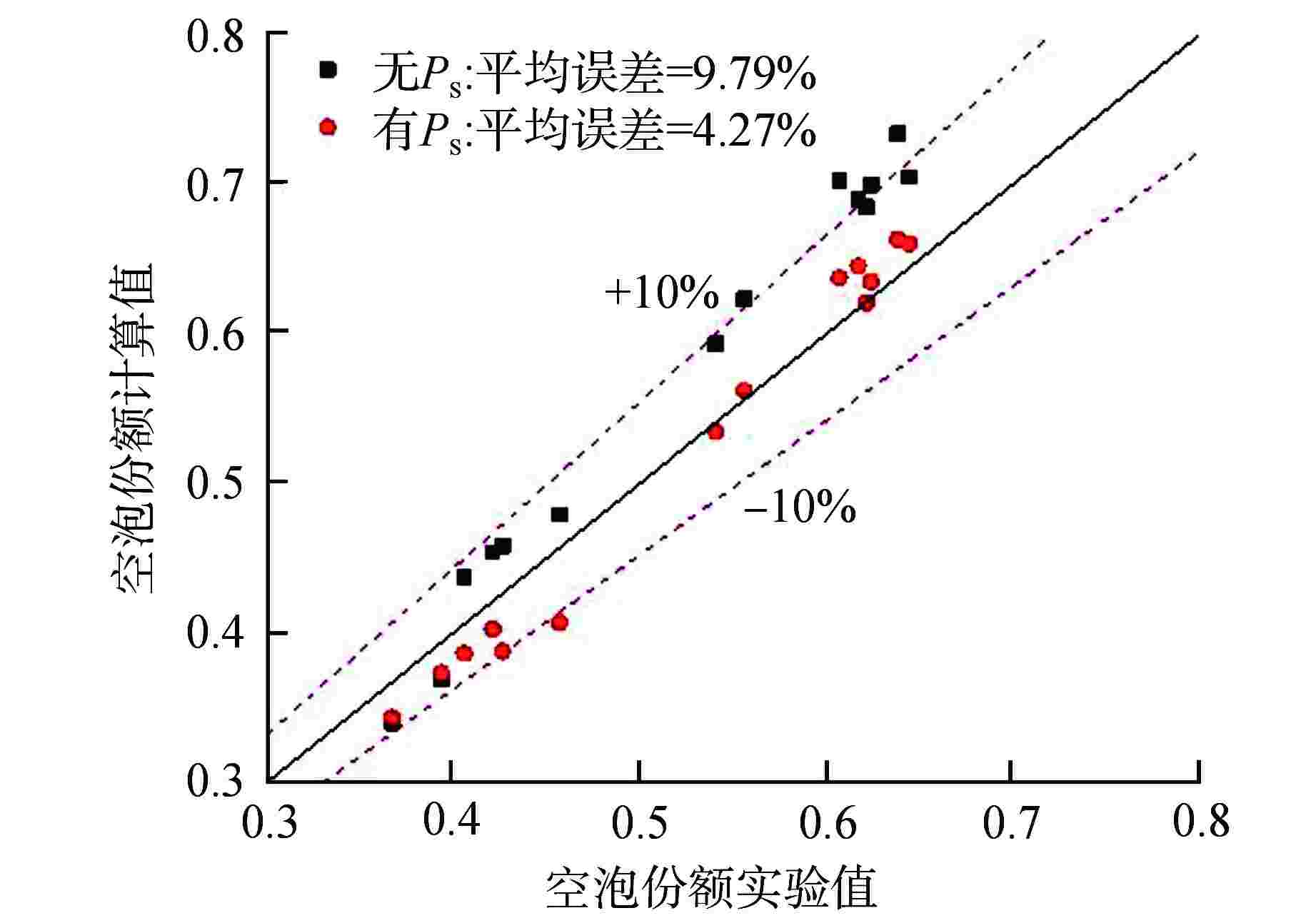
摘要: 一维两流体模型中，界面阻力是决定相间耦合程度的关键参数，其计算方法目前有漂移流模型法和阻力系数法。本研究利用子通道程序，基于圆管空气-水两相实验数据，对这2种计算方法进行了评估，结果表明一维两流体模型中漂移流模型法的预测能力要优于阻力系数法。同时评估了两相流动中分布效应对界面阻力计算的影响，结果表明在低空泡份额区分布效应影响较小，而高空泡份额区其影响明显。Abstract: In one-dimensional two-fluid model, the interfacial resistance is a key parameter for determining the degree of coupling between phases. At present, the calculation methods include drift-flux model method and resistance coefficient method. In this study, by using the subchannel program, the two calculation methods are evaluated based on the circular tube air-water two-phase experimental data. The results show that the prediction ability of the drift-flux model method in the one-dimensional two-fluid model is better than that of the resistance coefficient method. At the same time, the influence of distribution effect on the calculation of interfacial resistance in two-phase flow is evaluated. The results show that the effect is small in the low void fraction region, but obvious in the high void fraction region.
-
图 1 THERMIT-3与TRACE的对比
Figure 1. Comparison of Calculated Results of THERMIT-3 and TRACE
图 2 不同模型与实验数据的对比（
$\left\langle \alpha \right\rangle < 0.3$ ）Figure 2. Comparison of Models and Experimental Data (
$\left\langle \alpha \right\rangle < 0.3$ )
图 3 不同模型与实验数据的对比（
$\left\langle \alpha \right\rangle > 0.3$ ）Figure 3. Comparison of Models and Experimental Data (
$\left\langle \alpha \right\rangle > 0.3$ )
图 4 分布效应的影响（
$\left\langle \alpha \right\rangle < 0.3$ )Figure 4. Influence of Distribution Effect (
$\left\langle \alpha \right\rangle < 0.3$ )
图 5 分布效应的影响（
$\left\langle \alpha \right\rangle > 0.3$ ）Figure 5. Influence of Distribution Effect (
$\left\langle \alpha \right\rangle > 0.3$ )表 1 分布参数和漂移速度
Table 1. Distribution Parameter and Drift Velocity
条件 分布参数 漂移速度 $\left\langle \alpha \right\rangle < 0.2$ ${C_0} = 1.2 - 0.2\sqrt {\dfrac{{{\rho _{\rm{g}}}}}{{{\rho _{\rm{f}}}}}} $ ${\left\langle {\left\langle {{v_{{\rm{gj}}}}} \right\rangle } \right\rangle _{\rm{B}}} = \sqrt 2 \left( {\dfrac{{\sigma g\Delta \rho }}{{{\rho _{\rm{f}}}^2}}} \right){\left( {1 - \left\langle \alpha \right\rangle } \right)^{1.75}}$ $\left\langle \alpha \right\rangle > 0.3$ 当$D_{\rm{h}}^*$≤30：
${C_0} = 1.2 - 0.2\sqrt {\dfrac{{{\rho _{\rm{g}}}}}{{{\rho _{\rm{f}}}}}} $
当$D_{\rm{h}}^* > 30$：
${C_0} = {C_\infty } - \left( {{C_\infty } - 1} \right)\sqrt {\dfrac{{{\rho _{\rm{g}}}}}{{{\rho _{\rm{f}}}}}} $
${C_\infty } = 1 + 0.2{\left[ {\dfrac{{{\rho _{\rm{f}}}{{\left( {g{D_{\rm{h}}}} \right)}^{1/2}}}}{{\left| G \right| + 0.001}}} \right]^{1/2}}$当${N_{{\mu _{\rm{f}}}}} \leqslant 2.2 \times {10^{ - 3}}$：
${\left\langle {\left\langle {{v_{{\rm{gj}}}}} \right\rangle } \right\rangle _{\rm{C}}} = 0.0019 \cdot \min {\left( {30,D_{\rm{h}}^{\rm{*}}} \right)^{0.809}}{\left( {\dfrac{{{\rho _{\rm{g}}}}}{{{\rho _{\rm{f}}}}}} \right)^{ - 0.157}}{\left( {{N_{{\mu _{\rm{f}}}}}} \right)^{ - 0.562}}{\left( {\dfrac{{\sigma g\Delta \rho }}{{{\rho _{\rm{f}}}^2}}} \right)^{1/4}}$
当${N_{{\mu _{\rm{f}}}}} > 2.2 \times {10^{ - 3}}$：
${\left\langle {\left\langle {{v_{gj}}} \right\rangle } \right\rangle _C} = 0.35{\left[ {\dfrac{{g{D_{\rm{h}}}\Delta \rho }}{{{\rho _{\rm{f}}}}}} \right]^{1/2}}$
$D_{\rm{h}}^* = \dfrac{{{D_{\rm{h}}}}}{{\sqrt {\dfrac{\sigma }{{g\Delta \rho }}} }}$，${N_{{\mu _{\rm{f}}}}} = \dfrac{{{\mu _{\rm{f}}}}}{{{{\left( {{\rho _{\rm{f}}}\sigma \sqrt {\dfrac{\sigma }{{g\Delta \rho }}} } \right)}^{1/2}}}}$，$\Delta \rho = {\rho _{\rm{f}}} - {\rho _{\rm{g}}}$0.2≤$\left\langle \alpha \right\rangle $≤0.3 ${C_0} = 1.2 - 0.2\sqrt {\dfrac{{{\rho _{\rm{g}}}}}{{{\rho _{\rm{f}}}}}} $ $\left\langle {\left\langle { {v_{ {\rm{gj} } } } } \right\rangle } \right\rangle = w_{\rm{f} } \cdot {\left\langle {\left\langle { {v_{ {\rm{gj} } } } } \right\rangle } \right\rangle _{\rm{B} } } + \left( {1 - w_{\rm{f} } } \right) \cdot {\left\langle {\left\langle { {v_{ {\rm{gj} } } } } \right\rangle } \right\rangle _{\rm{C} } }$
$w_{\rm{f} } = \dfrac{ {0.3 - \left\langle \alpha \right\rangle } }{ {0.3 - 0.2} }$$D_{\rm{h}}^*$—无量纲当量直径Dh；${C_\infty }$—充分发展时的分布参数；${N_{{\mu _{\rm{f}}}}}$—无量纲液相粘性系数；wf—权值；σ—表面张力；G—质量流量；下标B—泡状流；下标C—帽状流 
下载: 导出CSV
表 2 实验数据汇总
Table 2. Summary of Experimental Data
作者 圆管管径/cm 工况选取范围 TALLEY 2.54，4.83，10.16，15.24，20.32 ${\rm{0 < }}\left\langle \alpha \right\rangle < 0.{\rm{4}}$ MATTHEW 4.83，5.08 ${\rm{0}}{\rm{.3 < }}\left\langle \alpha \right\rangle < 0.7$ DANG 2.54 ${\rm{0}}{\rm{.5 < }}\left\langle \alpha \right\rangle < 0.7$
下载: 导出CSV
-
[1] ISHII M, HIBIKI T. Thermo-fluid dynamics of two-phase flow[M]. New York: Springer, 2011: 444-448. [2] WALLIS G B. One-dimensional two-phase flow[M]. New York: McGraw-Hill, 1969: 315-323. [3] ISHII M, MISHIMA K. Two-fluid model and hydrodynamic constitutive relations[J]. Nuclear Engineering and Design, 1984, 82(2-3): 107-126. doi: 10.1016/0029-5493(84)90207-3 [4] BROOKS C S, HIBIKI T, ISHII M. Interfacial drag force in one-dimensional two-fluid model[J]. Progress in Nuclear Energy, 2012, 61: 57-68. doi: 10.1016/j.pnucene.2012.07.001 [5] BAJOREK S. TRACE V5.0 theory manual, field equation, solution methods and physical models[R]. Washington: Nuclear Regulatory Commission, 2007. [6] Nuclear Regulatory Commission. RELAP5/MOD3 code manual: user’s guide and input requirements. Volume 2: NUREG/CR-5535, INEL-95/0174[R]. Washington: Nuclear Regulatory Commission, 1995. [7] HIBIKI T, ISHII M. One-dimensional drift-flux model and constitutive equations for relative motion between phases in various two-phase flow regimes[J]. International Journal of Heat and Mass Transfer, 2003, 46(25): 4935-4948. doi: 10.1016/S0017-9310(03)00322-3 [8] KATAOKA I, ISHII M. Drift flux model for large diameter pipe and new correlation for pool void fraction[J]. International Journal of Heat and Mass Transfer, 1987, 30(9): 1927-1939. doi: 10.1016/0017-9310(87)90251-1 [9] ISHII M, CHAWLA T C. Local drag laws in dispersed two-phase flow: NUREG/CR-1230, ANL-79-105[R]. Washington: Argonne National Laboratory, 1979. [10] KELLY J E, KAO S P, KAZIMI M S. THERMIT-2: A two-fluid model for light water reactor subchannel transient analysis: MIT-EL-81-014[R]. USA: MIT Energy Laboratory Electric Utility Program, 1981. [11] TALLEY J D. Interfacial area transport equation for vertical and horizontal bubbly flows and its application to the TRACE Code[D]. Pennsylvania: The Pennsylvania State University, 2012. [12] BERNARD M S. Implementation of the interfacial area transport equation in trace for boiling two-phase flows[D]. Pennsylvania: The Pennsylvania State University, 2014. [13] DANG Z R, WANG G Y, JU P, et al. Experimental study of interfacial characteristics of vertical upward air-water two-phase flow in 25.4 mm ID round pipe[J]. International Journal of Heat and Mass Transfer, 2017, 108: 1825-1838. doi: 10.1016/j.ijheatmasstransfer.2017.01.040 [14] ZUBER N, FINDLAY J A. Average volumetric concentration in two-phase flow systems[J]. Journal of Heat Transfer, 1965, 87(4): 453-468. doi: 10.1115/1.3689137 -
计量
- 文章访问数: 196
- HTML全文浏览量: 95
- PDF下载量: 40
- 被引次数: 0
