Numerical Simulation Research on Flow-Induced Vibration Characteristics of Fluid-Conveying Pipe Network
-
摘要: 为研究管路系统流质振动特性以优化管路设计，本文以典型输液管网系统为对象，基于Ansys Workbench平台开展了不同流体激励下的管路双向流固耦合模拟计算，获得了管路结构流致振动特性，分析讨论了激励类型、介质温度、流场结构及结构固有频率对管内流致振动特性的影响。结果表明，脉动流量激励下的管路结构振幅显著大于恒定流量激励下的结构振幅，当流体激励频率较接近管路结构固有频率时，结构和流体将趋于共振，导致结构振动加剧。通过在管道适当位置施加约束支撑，使结构固有频率远离流体激励频率，可有效减小管道的振动。此外，介质温度和流速对结构振幅有较大影响。
-
关键词:
- 流体激励 /
- 输流管网 /
- 双向流固耦合 /
- 流致振动 /
- Ansys Workbench
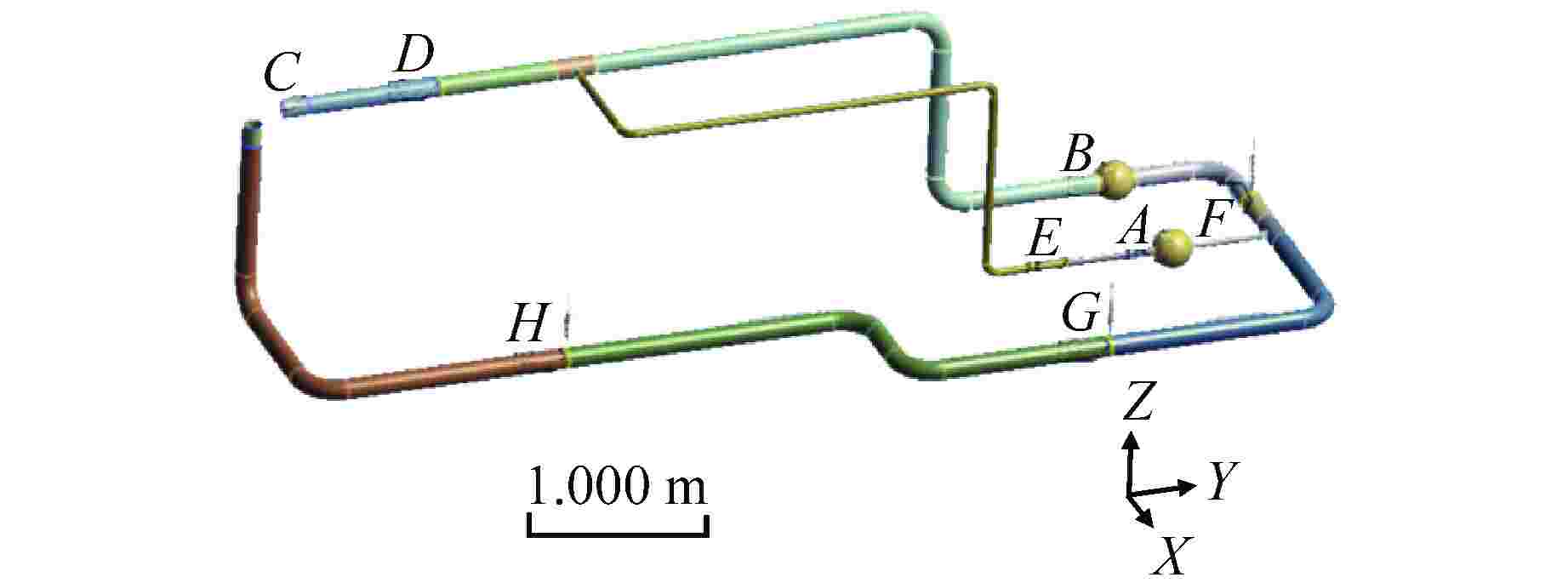
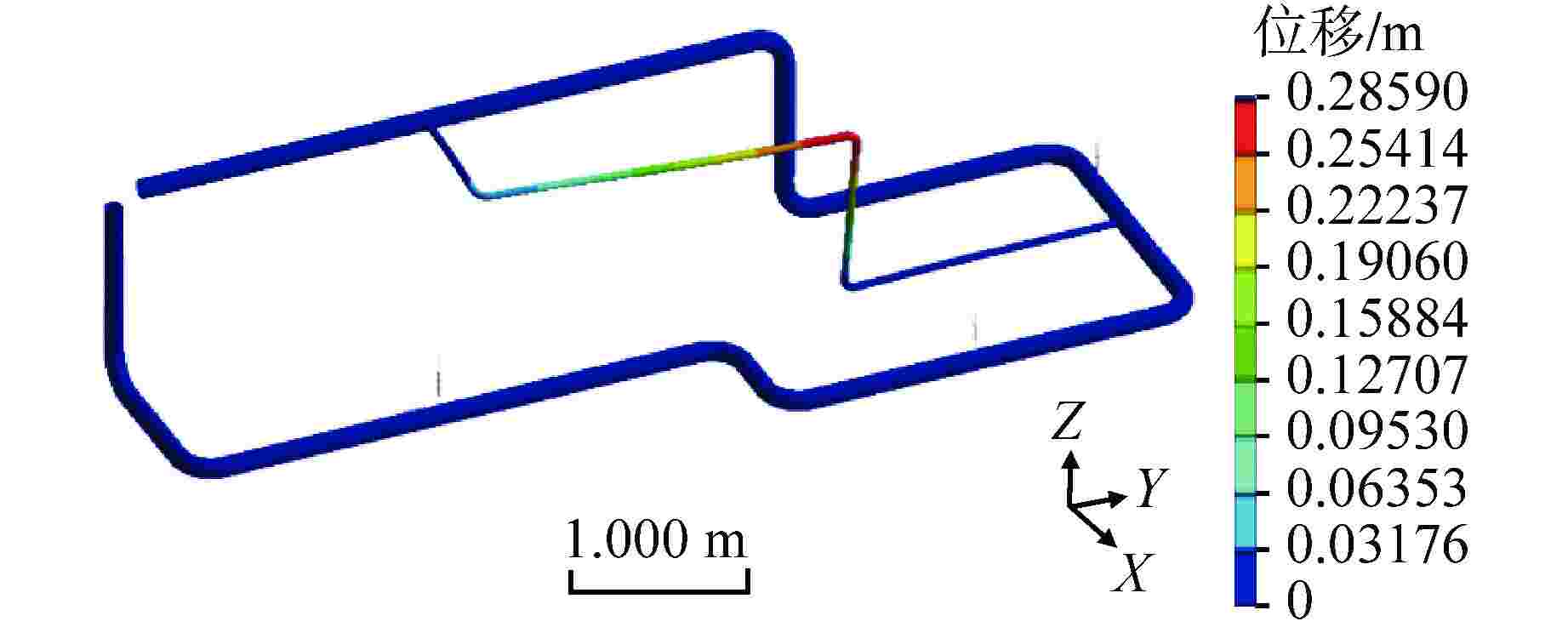
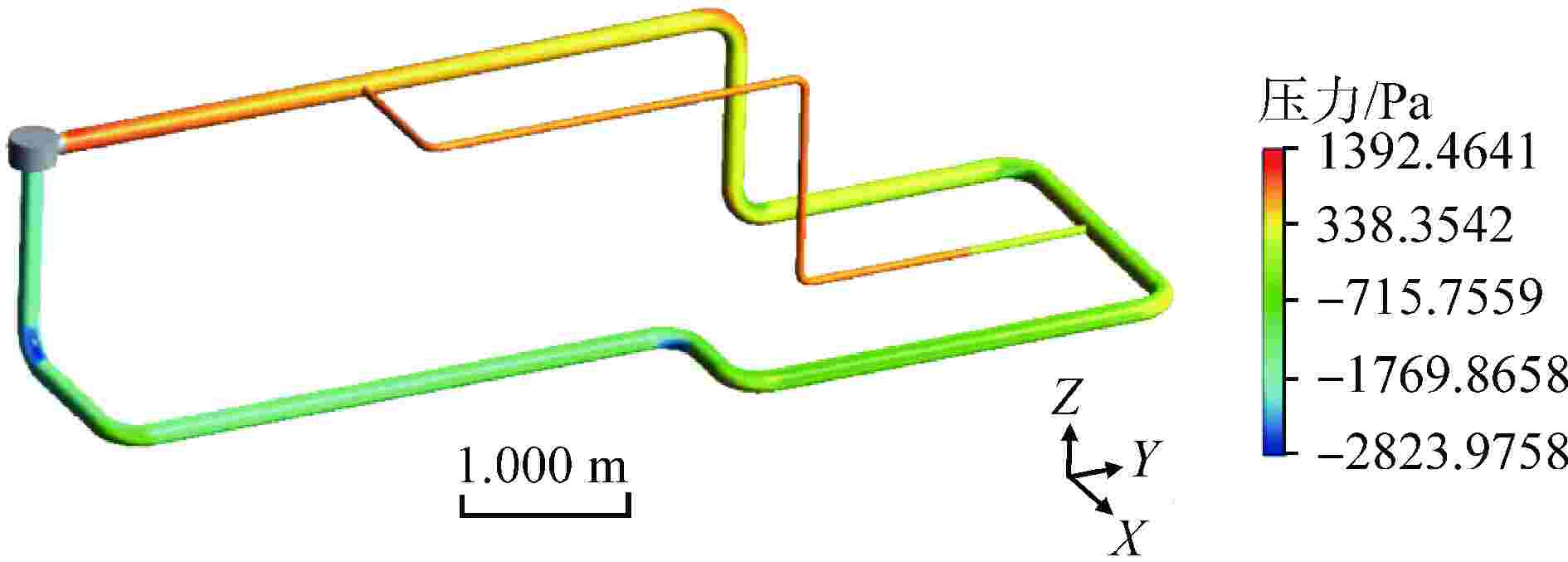
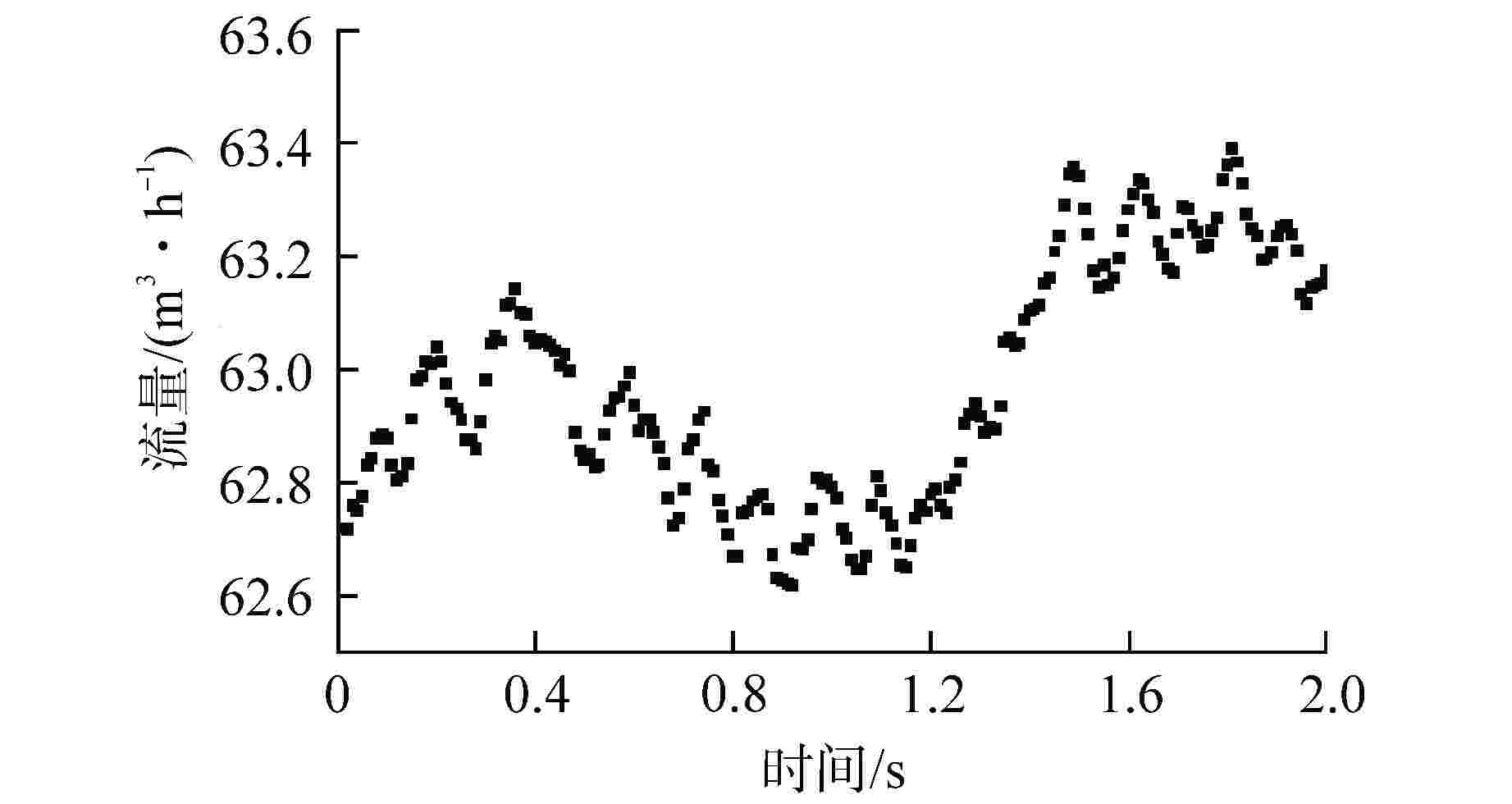
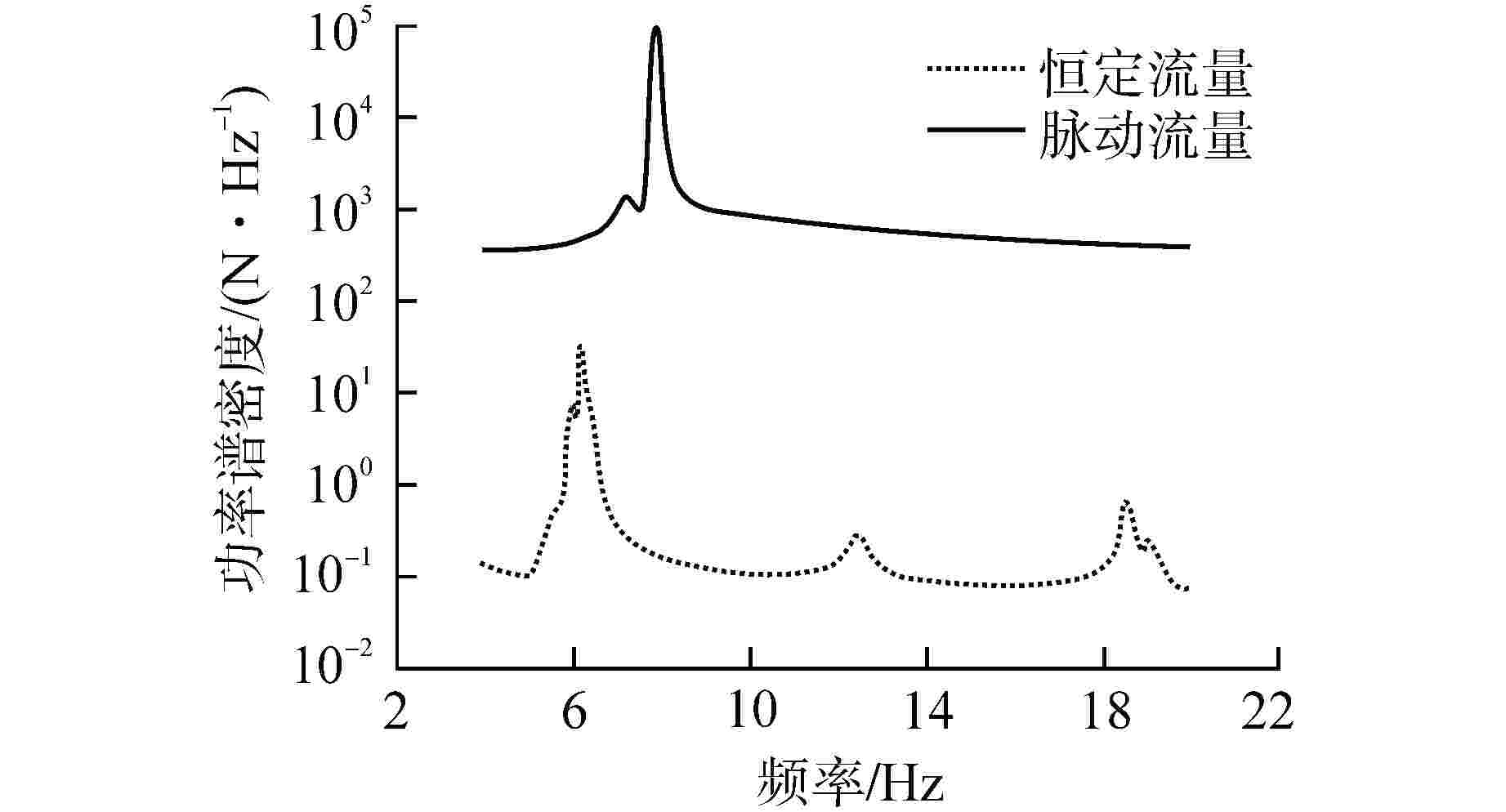
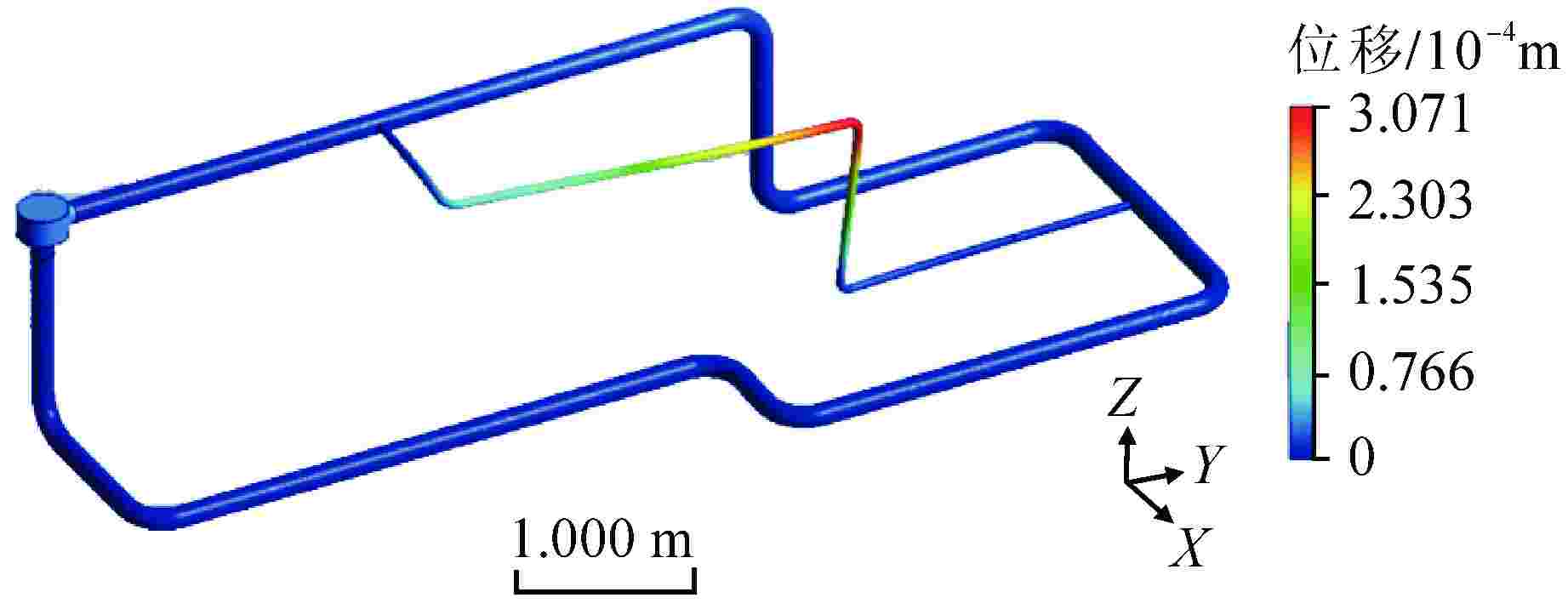
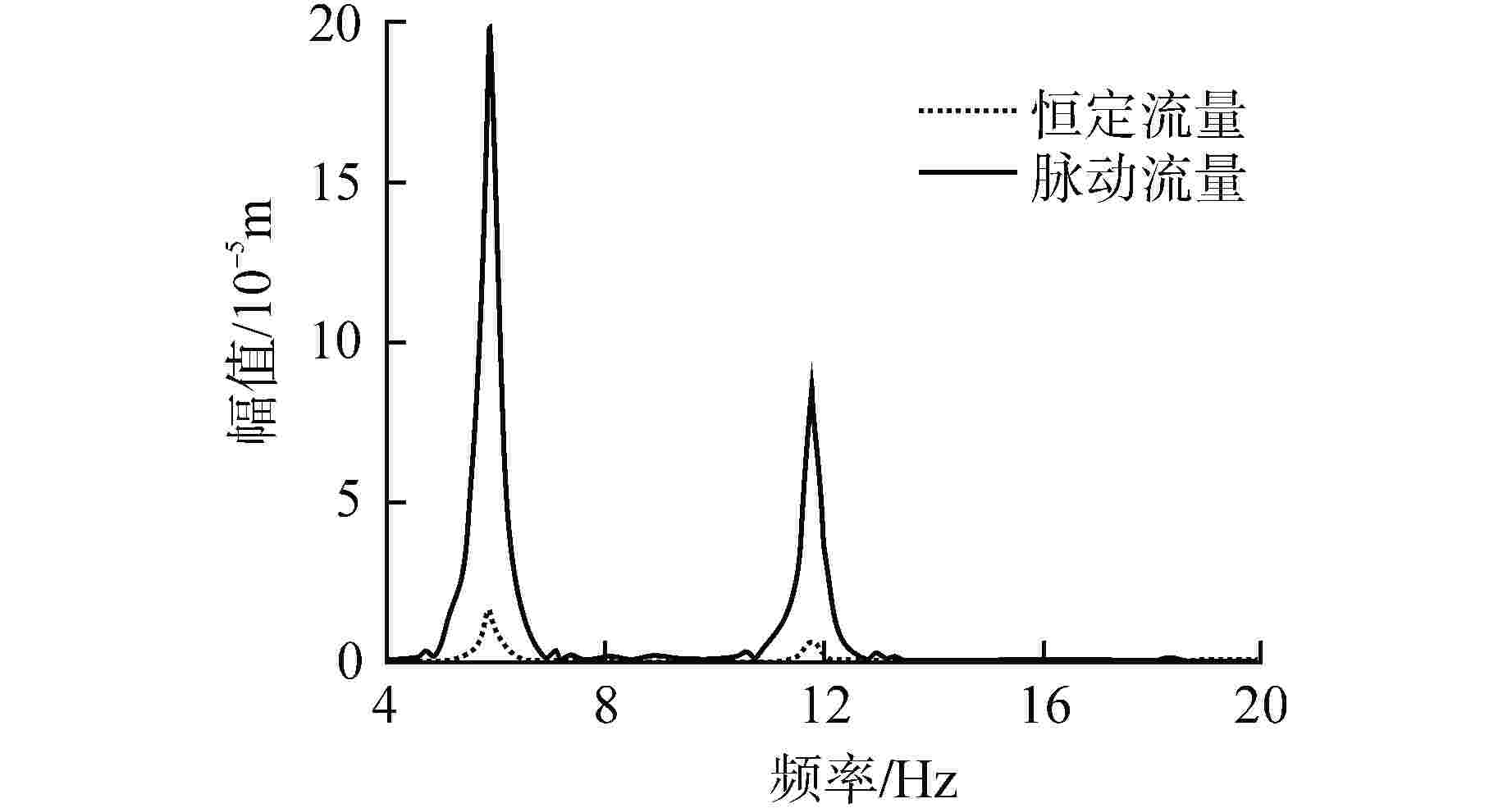
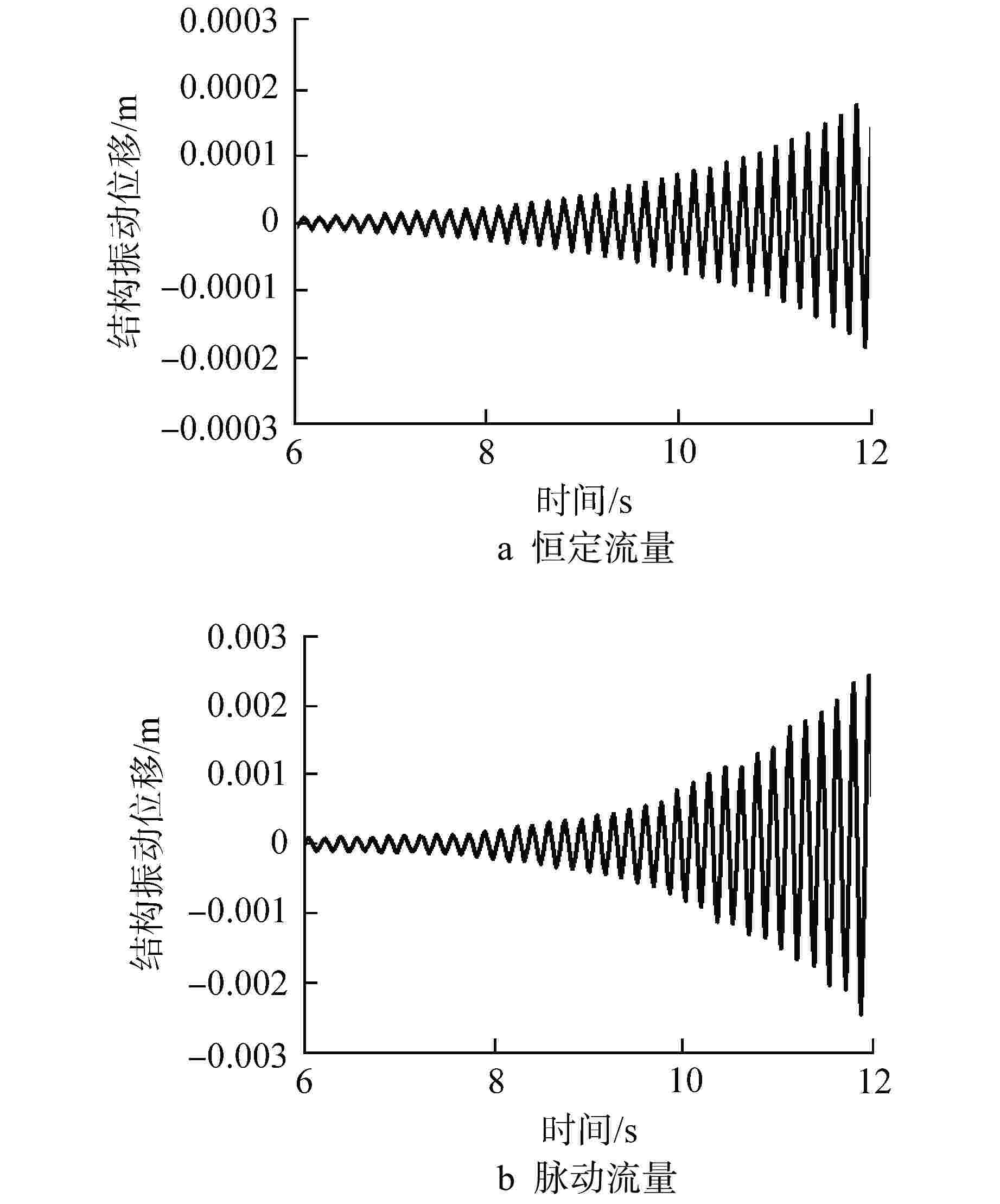
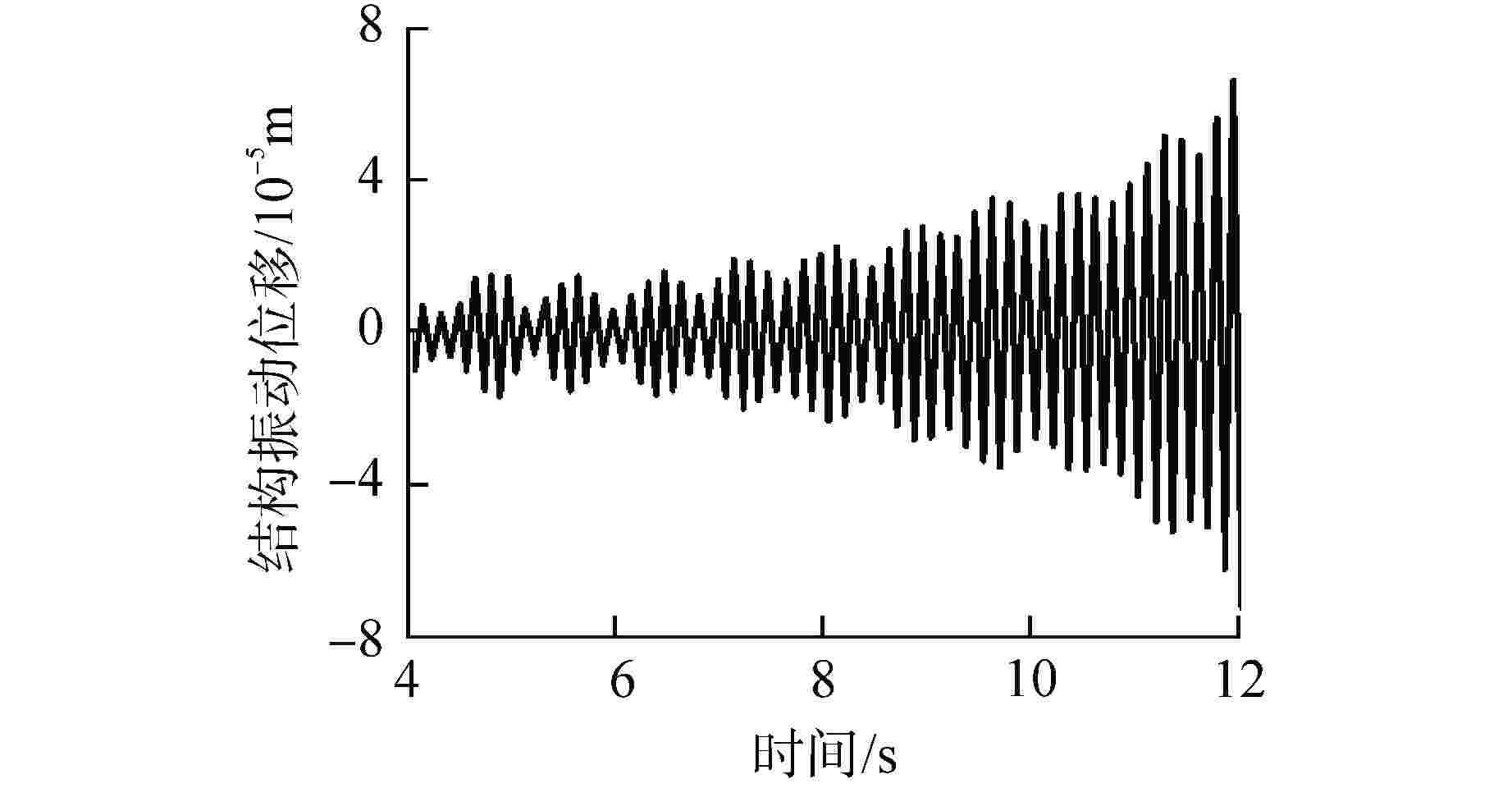
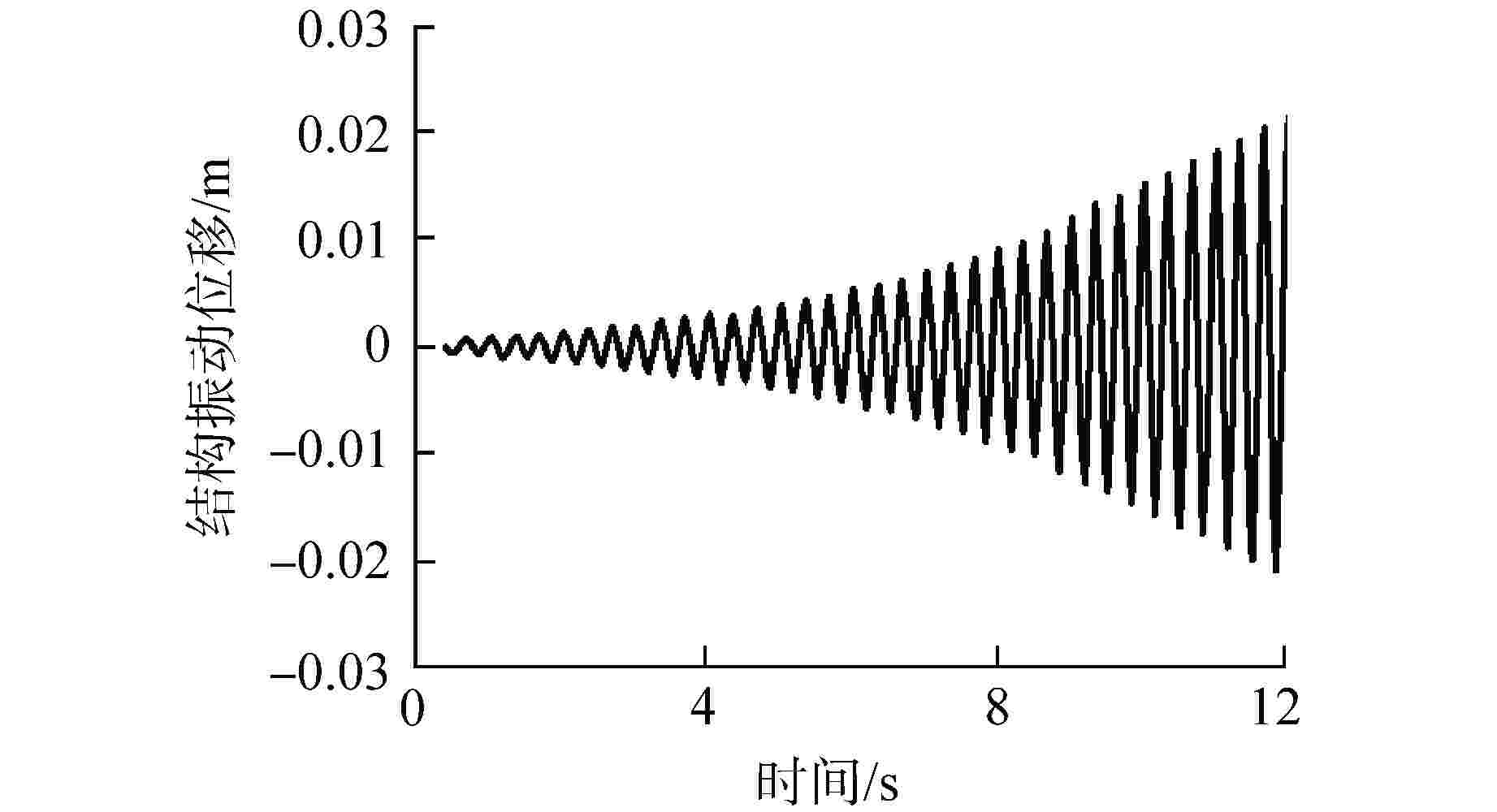
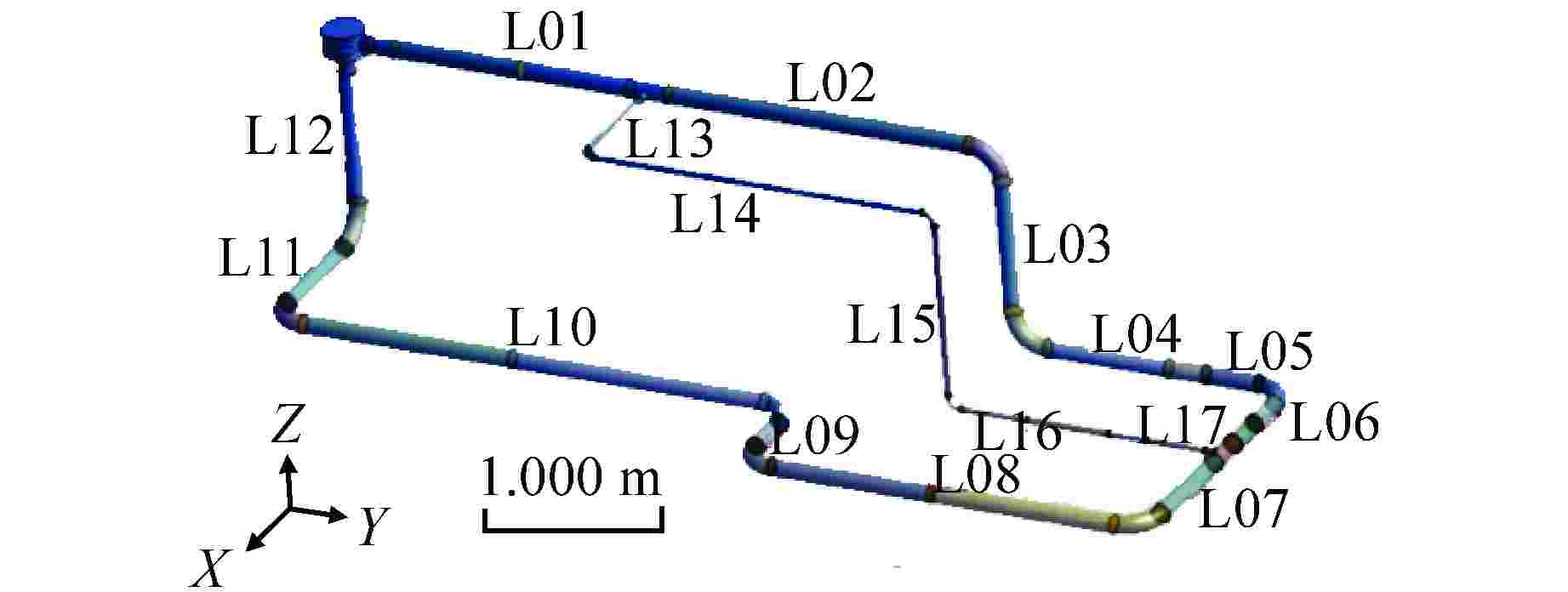
Abstract: To study flow-induced vibration characteristics of pipeline system for pipeline optimization design, two-way fluid-structure interaction numerical simulation for the typical fluid-conveying pipe network with various fluid excitation was conducted based on Ansys Workbench, and the flow-induced vibration characteristics of the pipeline structure were obtained. The effects of excitation type, medium temperature, flow field structure and natural frequency of structure on the fluid-induced vibration characteristics in the pipe were analyzed and discussed. The results show that the structural amplitude of pipeline under excitation of pulsating flow is significantly larger than that under constant flow. When the frequency of fluid excitation is close to the natural frequency of the pipeline structure, the structure and fluid tend to resonate, leading to increased structural vibration. By applying constraint support at the appropriate position of the pipeline, the natural frequency of the structure is far away from the fluid excitation frequency, which can effectively reduce the vibration of the pipeline. In addition, the medium temperature and flow velocity have a great influence on the structural amplitude. -
图 4 管路系统稳态流场压力分布
Figure 4. Pressure Distribution of Steady Flow Field of Pipeline System
图 7 管道结构最大位移示意图
Figure 7. Schematic Diagram of Maximum Displacement of the Pipeline Structure
图 8 结构振动位移频域特性曲线
Figure 8. Frequency-Domain Characteristic Curve of Structural Vibration Displacement
图 9 结构振动位移时域特性曲线
Figure 9. Time-Domain Characteristic Curve of Structural Vibration Displacement
图 10 介质温度为300℃时结构振动位移时域特性曲线
Figure 10. Time-Domain Characteristic Curve of Structural Vibration Displacement at 300℃ of Medium Temperature
-
[1] PAÏDOUSSIS M P, LI G X. Pipes conveying fluid: a model dynamical problem[J]. Journal of Fluids and Structures, 1993, 7(2): 137-204. doi: 10.1006/jfls.1993.1011 [2] ASHLIY H, HACILLAND G. Bend vibration of a containing flowing fliud[J]. Journal of Applied Mechanics, 1950(17): 229-232. doi: 10.1115/1.4010122 [3] 俞树荣,马璐,余龙. 弯曲输流管道流固耦合动力特性分析[J]. 噪声与振动控制,2015, 35(4): 43-47. [4] 刘桂祥,张鲲,林松. 基于CFD和结构有限元双向耦合方法的载流管路流致振动特性研究[J]. 核动力工程,2016, 37(S2): 24-27. [5] 窦益华,于凯强,杨向同,等. 输流弯管流固耦合振动有限元分析[J]. 机械设计与制造工程,2017, 46(2): 18-21. doi: 10.3969/j.issn.2095-509X.2017.02.003 [6] 胡兵, 郁殿龙. 流固耦合管路振动传递特性研究[C]//第十三届全国振动理论及应用学术会议论文集. 西安: 中国振动工程学会, 2019. [7] 韩天宇. 基于Workbench的流固耦合作用下输流管道振动特性分析[D]. 衡阳: 南华大学, 2020. -
下载:
计量
- 文章访问数: 702
- HTML全文浏览量: 216
- PDF下载量: 110
- 被引次数: 0
