Transient Simulation Study of Primary Loop Nitrogen-typed Pressurization System
-
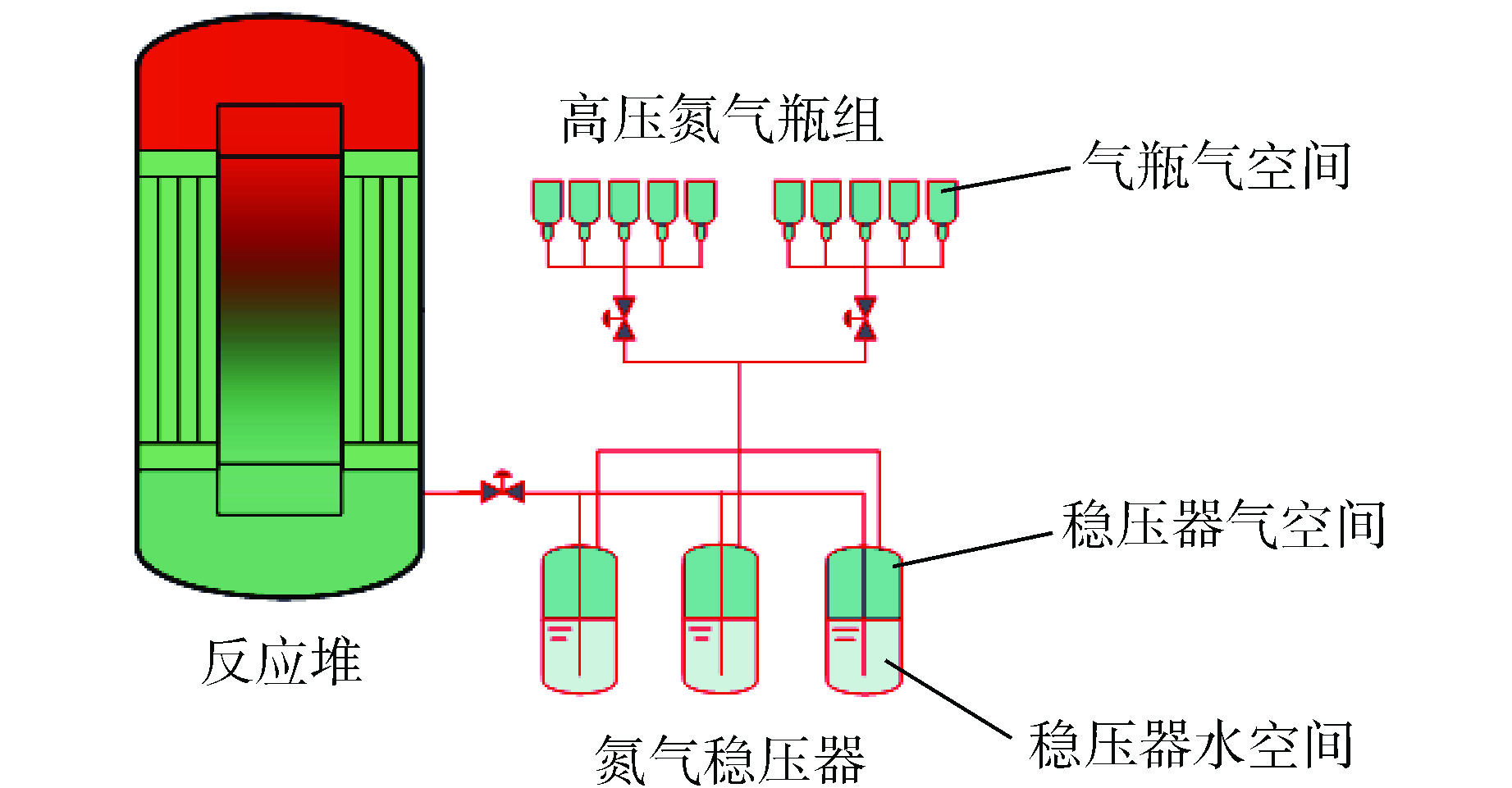
摘要: 基于氮气稳压基本原理，采用集总参数法开发了氮气稳压系统瞬态模拟程序，该模型突破了现有独立稳压器模型的局限，实现了一回路系统与氮气稳压器的直接耦合，并采用浮动式核电站氮气稳压系统试验数据对程序进行了验证。在此基础上，提出了一种基于敏感性分析的氮气稳压系统设计方法，与现有设计方法相比，该设计方法可以得到氮气稳压系统的优化配置方案，同时通过适配性设计，可以确保氮气稳压系统在启动过程中，压力不超过一回路系统温度压力限制曲线。Abstract: Based on the fundamental of nitrogen pressure stabilizing, the lumped parameter method is adopted to develop the nitrogen pressure stabilizing system transient simulation model, which breaks through the limitations of the existing independent stabilizer model, realizes the direct coupling between the primary loop system and the nitrogen stabilizer, and verifies the program with the test data of the nitrogen pressure stabilizing system of the floating nuclear power plant. On this basis, a design method of nitrogen pressure stabilizing system based on sensitivity analysis is proposed. Compared with the existing design method, this design method can obtain the optimal configuration scheme of nitrogen pressure stabilizing system. At the same time, through the adaptive design, it can ensure that the pressure of the nitrogen pressure stabilizing system does not exceed the range of the temperature and pressure limit curve of the primary loop system during the start-up process.
-
Key words:
- Reactor /
- Nitrogen pressure stabilizing /
- Transient simulation /
- Cold start up
-
图 3 氮气稳压系统温度变化对比
Figure 3. Comparison of Temperature Variation of Nitrogen Pressure Stabilizing System
图 7 冷启动过程压力温度分布图（RRA调整后）
Figure 7. Pressure and Temperature Distribution during Cold Start (RRA Adjusted)
表 2 氮气稳压系统优化配置方案
Table 2. Optimal Configuration Scheme of Nitrogen Pressure Stabilizing System
参数名称 数据 氮气稳压器初始压力/MPa 2.4 氮气稳压器总容积/m3 6.8 氮气稳压器初始水容积/m3 0.5 高压气瓶容积/m3 0 
下载: 导出CSV
-
[1] 张大林,秋穗正,苟军利,等. 新型氮气稳压器系统稳态和瞬态特性研究[J]. 核动力工程,2006, 27(S1): 38-42. [2] 聂春福. 压水堆蒸汽式稳压器[J]. 核动力工程,1987, 8(3): 24-34. [3] 尤洪君,霍震华,程轶平. 核动力稳压器多区非平衡模型[J]. 核动力工程,2001, 22(2): 133-137. doi: 10.3969/j.issn.0258-0926.2001.02.009 [4] 林诚格. 非能动安全先进核电厂AP1000[M]. 北京: 中国原子能出版社, 2008: 337-338. [5] 广东核电培训中心. 900MW压水堆核电站系统与设备[M]. 北京: 中国原子能出版社, 2005: 262-263. -
图(7) / 表(2)
计量
- 文章访问数: 903
- HTML全文浏览量: 89
- PDF下载量: 79
- 被引次数: 0
