基于Hilbert-Huang变换和BP神经网络的核级电动阀门退化趋势预测

刘杰; 张林; 王运生; 闫晓; 湛力; 欧柱

doi:10.13832/j.jnpe.2022.03.0179

基于Hilbert-Huang变换和BP神经网络的核级电动阀门退化趋势预测

doi: 10.13832/j.jnpe.2022.03.0179

刘杰^1,,
张林^{1, 2},
王运生^1, ,,
闫晓¹,
湛力¹,
欧柱¹

1.
中国核动力研究设计院，成都，610213
2.
电子科技大学，成都，611731

详细信息

作者简介:
刘　杰（1992—），男，助理研究员，主要从事机电设备可靠性研究，E-mail: liujie_cult@163.com

通讯作者:
王运生，E-mail: 153637760@qq.com

中图分类号: TL353⁺.11；TP183
计量
- 文章访问数: 327
- HTML全文浏览量: 212
- PDF下载量: 35
- 被引次数: 0
出版历程
- 收稿日期: 2021-03-25
- 录用日期: 2021-05-06
- 修回日期: 2022-03-14
- 刊出日期: 2022-06-07

Degradation Trend Prediction of Nuclear-level Electric Valve Based on Hilbert-Huang Transform and BP Neural Network

Liu Jie^1
,,
Zhang Lin^{1, 2},
Wang Yunsheng^{1
, ,},
Yan Xiao¹,
Zhan Li¹,
Ou Zhu¹

1.
Nuclear Power Institute of China, Chengdu, 610213, China
2.
University of Electronic Science and Technology of China, Chengdu, 611731, China

摘要

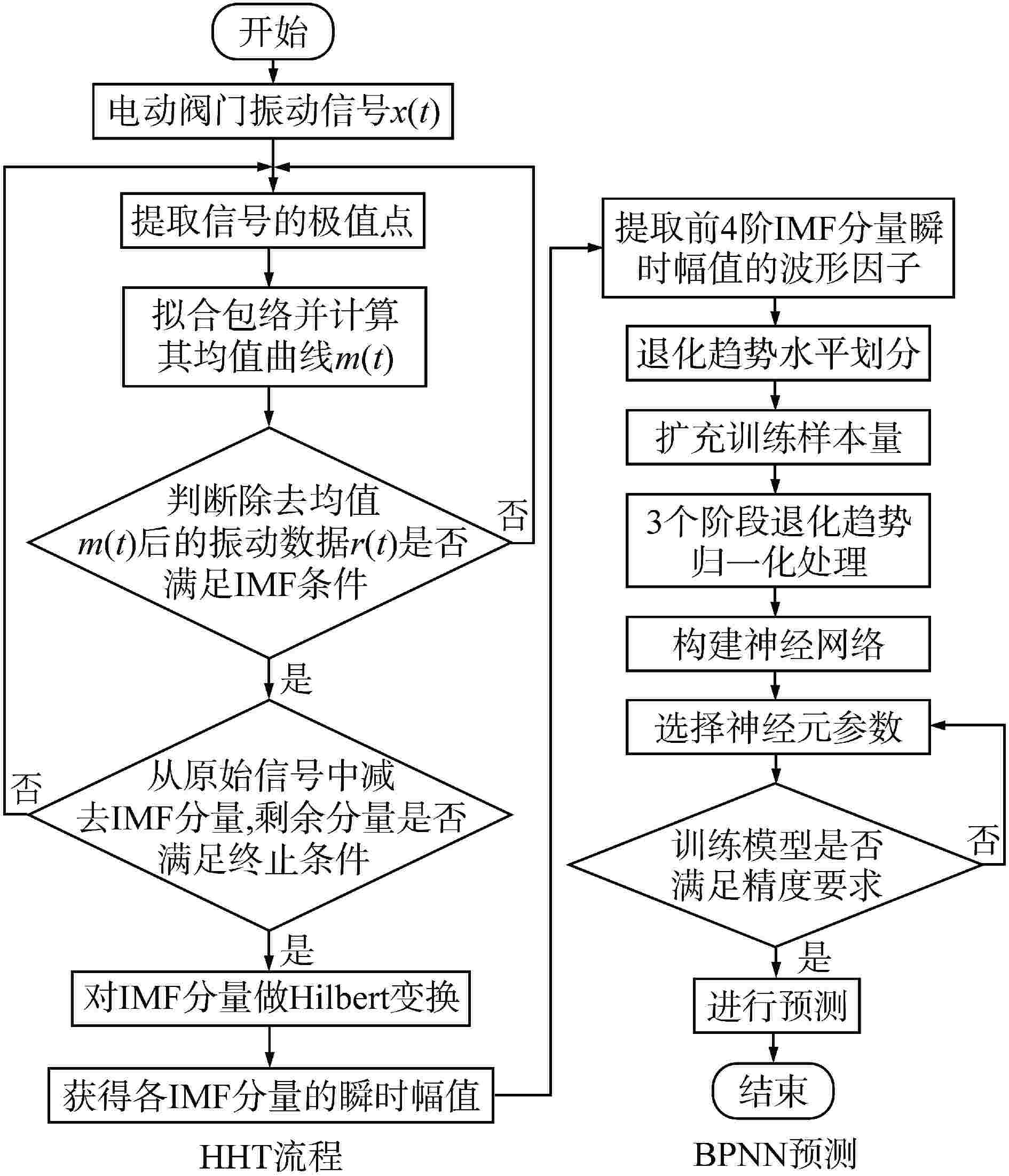
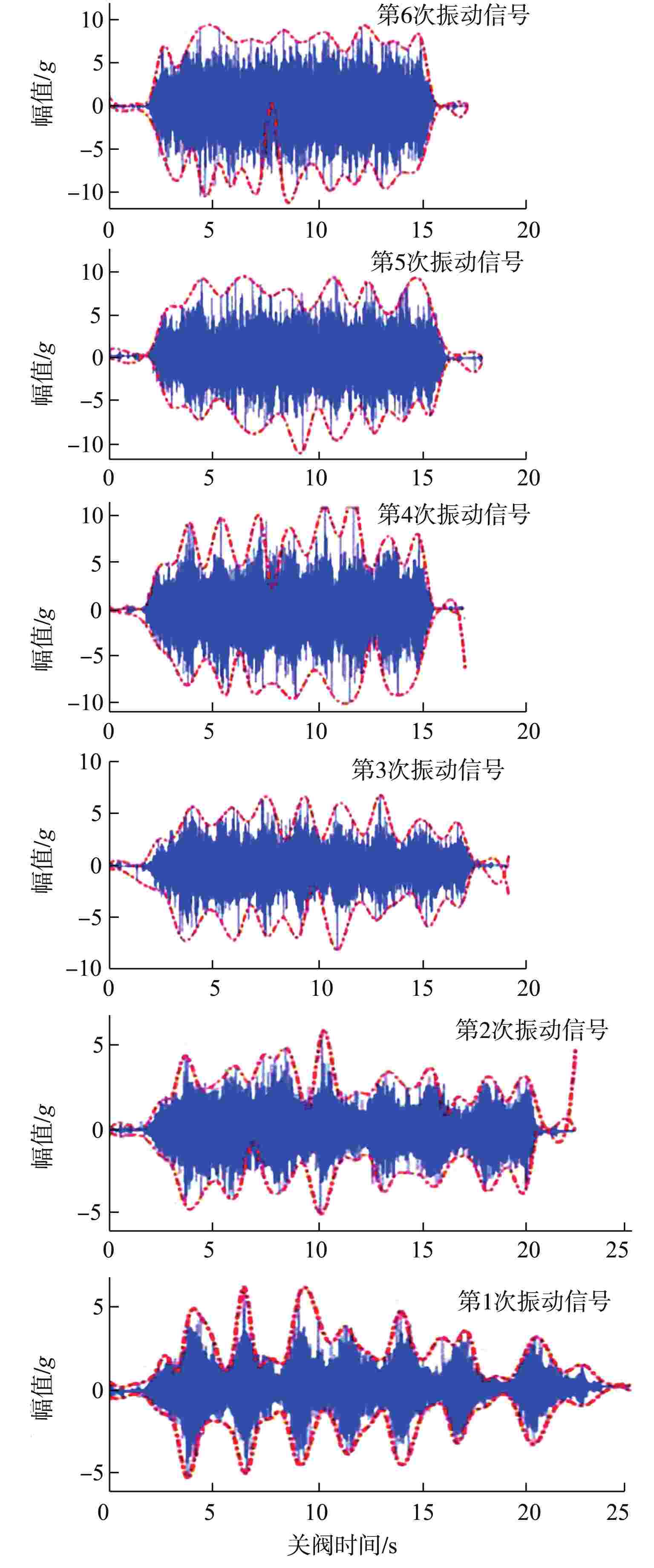
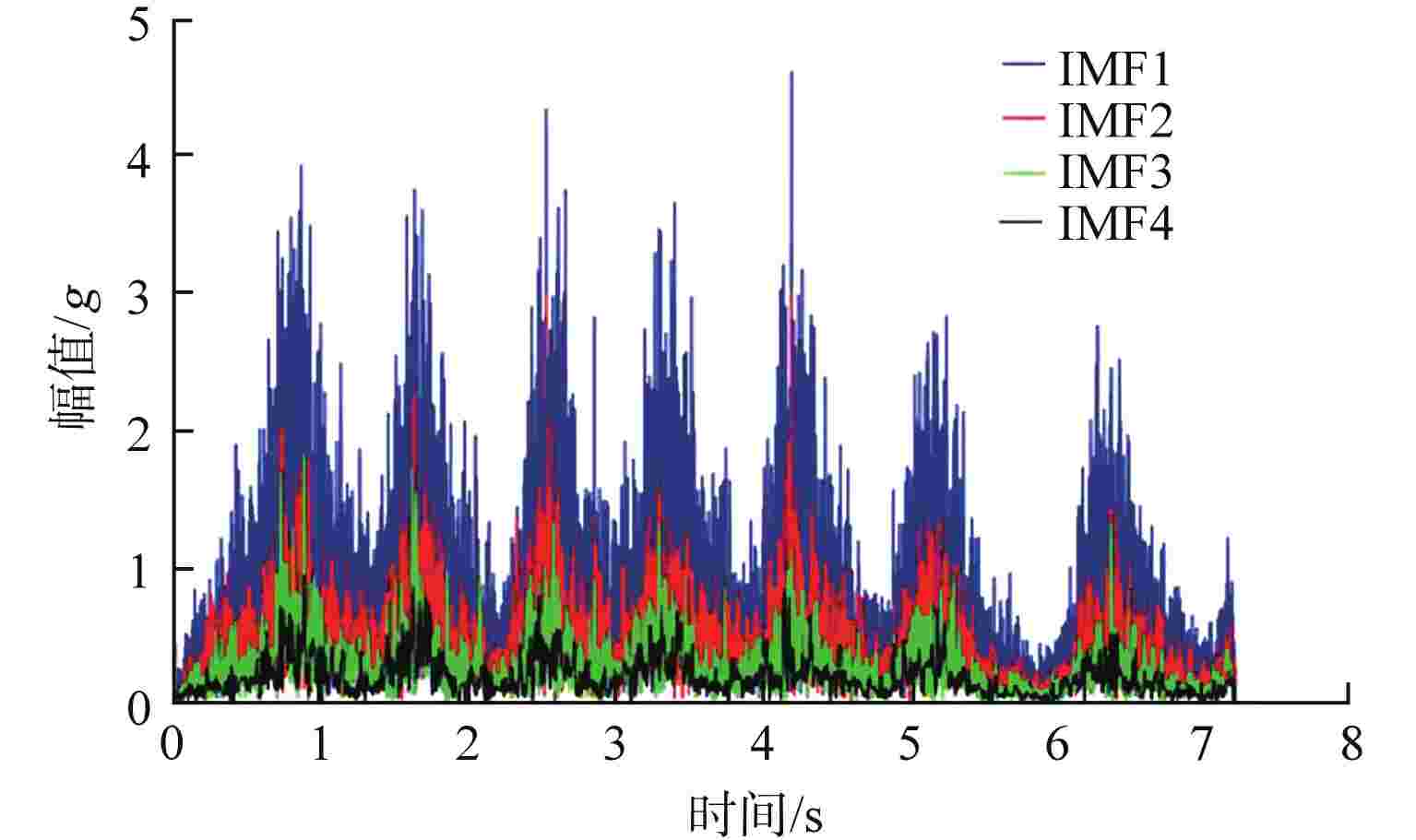
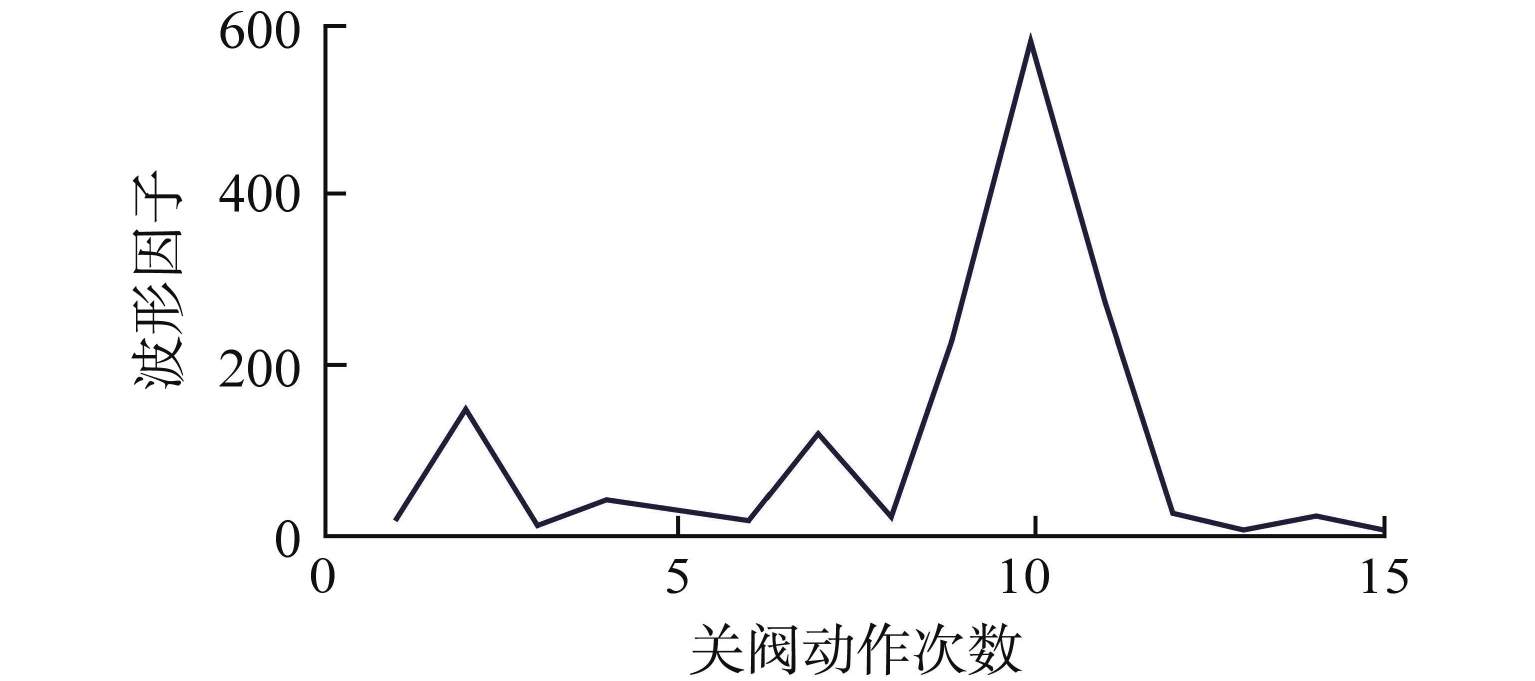
摘要: 核级电动阀门服役环境恶劣，极易发生退化失效。为准确预测核级电动阀门性能退化趋势，采用Hilbert-Huang变换（HHT）和反向传播神经网络（BPNN）相结合的方法（HHT-BPNN）对核级电动阀门的退化状态进行预测。本文采用某次核级电动阀门可靠性试验的振动信号对电动阀门退化趋势进行预测，结果显示该方法能准确预测出核级电动阀门的3种退化状态，且其相对误差在可接受范围内。研究表明HHT能够有效提取信号的退化信息，BPNN能够准确预测核级电动阀门的退化趋势，HHT-BPNN预测方法能有效解决核级电动阀门性能退化预测困难的问题。
- 核级电动阀门 /
- Hilbert-Huang变换（HHT） /
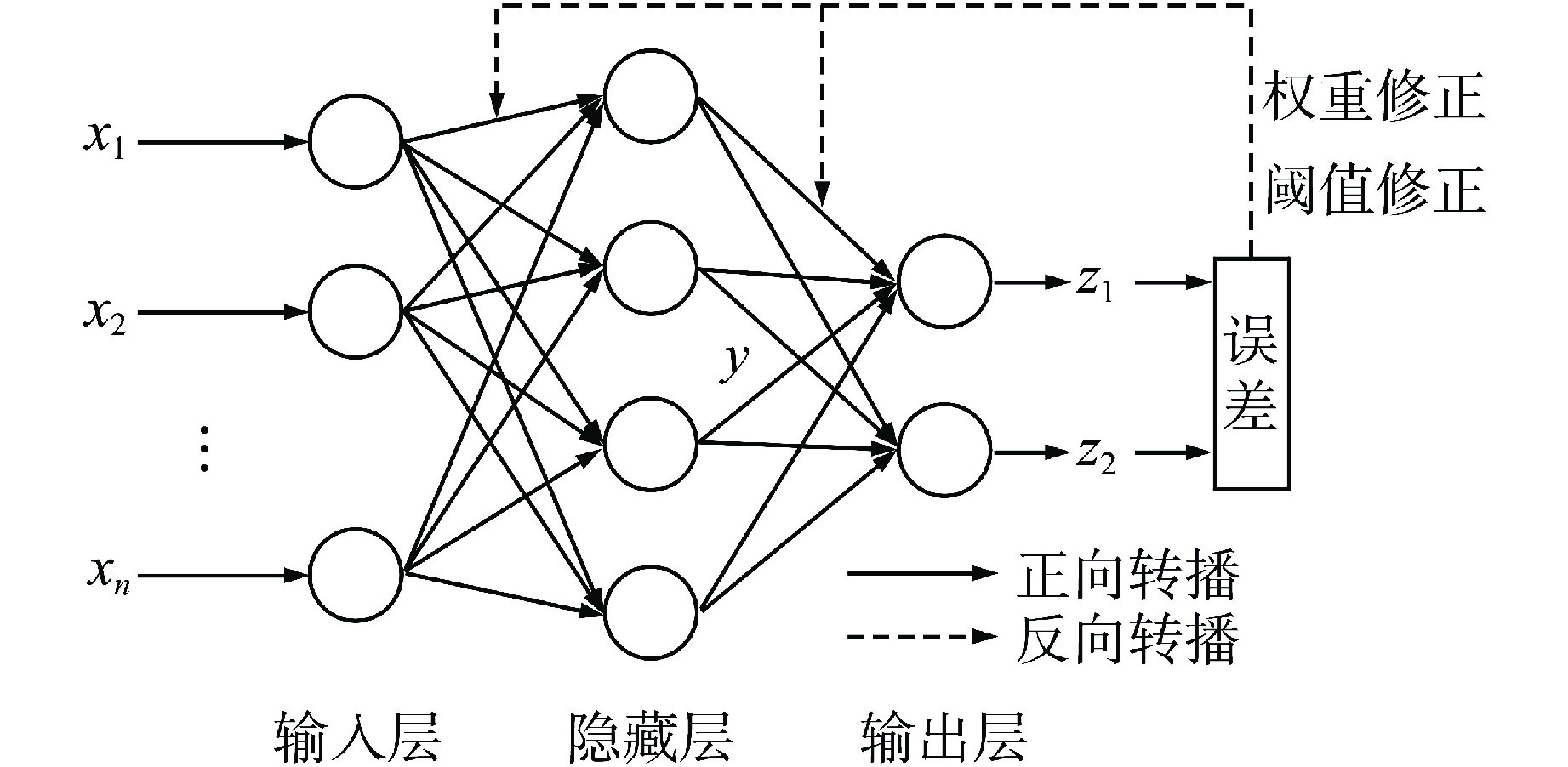
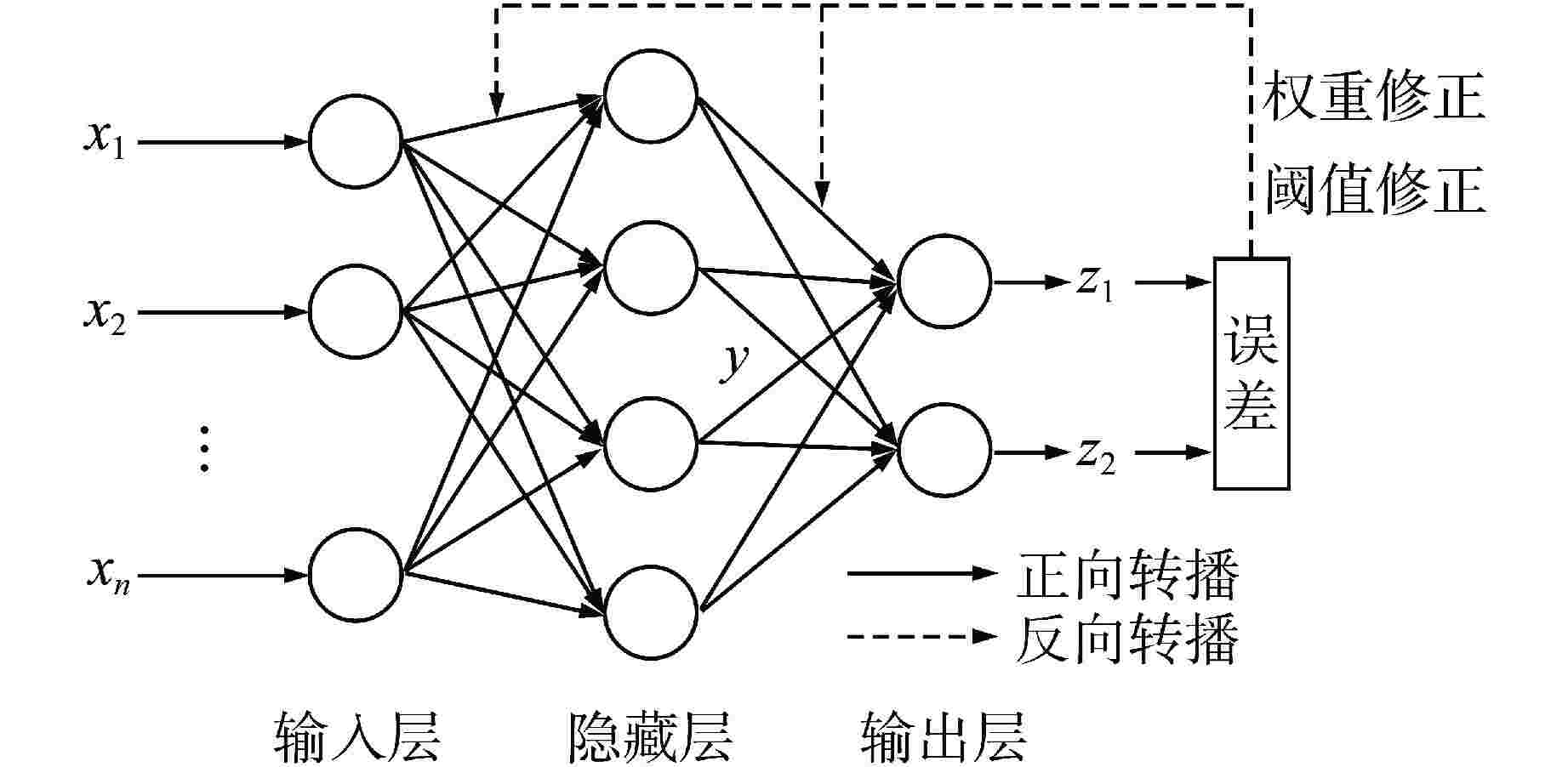
- 反向传播神经网络（BPNN） /
- 退化预测
Abstract: Due to the harsh service environment of nuclear-level electric valves, degradation and failure are easy to occur. Therefore, in order to accurately predict the performance degradation trend of nuclear-level electric valves, this study adopts a method based on Hilbert-Huang transform (HHT) and BP neural network (BPNN) combined method (HHT-BPNN) to predict the degradation state of nuclear-level electric valve. In this paper, the vibration signal of a nuclear-level electric valve reliability test is used to predict the degradation trend of the electric valve. The results show that the method can accurately predict the three degradation states of the nuclear-level electric valve, and the relative error is within the acceptable range. The analysis and research results show that HHT can effectively extract the degradation information of the signal, and BPNN can accurately predict the degradation trend of nuclear-level electric valves. The HHT-BPNN prediction method can effectively solve the difficulty of predicting the performance degradation of nuclear-level electric valves.
- Nuclear-level electric valve /
- Hilbert-Huang transform (HHT) /
- BP neural network (BPNN) /
- Degradation prediction

HTML全文

图 1 BPNN算法原理过程图

Figure 1. BPNN Algorithm Principle Process Diagram

下载: 全尺寸图片幻灯片

图 2 基于 HHT 和 BPNN 的预测方法

Figure 2. Prediction Method Based on HHT and BPNN

下载: 全尺寸图片幻灯片

图 3 电动阀门失效前 6 次振动退化数据

红色虚线——电动阀门关闭时振动信号的包络线

Figure 3. Six Vibration Degradation Data before Failure of Electric Valve

下载: 全尺寸图片幻灯片

图 4 前4组IMF分量Hilbert的瞬时幅值图

Figure 4. Hilbert’s Instantaneous Amplitude Map of IMF Components in the First Four Groups

下载: 全尺寸图片幻灯片

图 5 HHT瞬时幅值波形因子

Figure 5. Waveform Factor of HHT Instantaneous Amplitude

下载: 全尺寸图片幻灯片

图 6 原始振动信号波形因子

Figure 6. Waveform Factor of Original Vibration Signal

下载: 全尺寸图片幻灯片

表 1 优化后BPNN网络参数设置情况

Table 1. BPNN Network Parameter Setting after Optimization　　　　

参数	设置情况
输入信号向量维数	4
隐藏层数	3
隐藏层神经元个数	[4, 2, 2]
核函数类型	tansig函数
优化目标	根均方误差最小
训练优化算法	梯度下降法
迭代次数	5000

下载: 导出CSV

表 2 基于HHT-BPNN方法预测结果

Table 2. Prediction Results Based on HHT-BPNN Method

阀门失效前动作次数	验证指标值	预测输出值	相对误差/%
15	1	0.9991	0.09
14	1	1.0000	0
13	1	0.9984	0.16
12	1	1.0033	0.33
11	1	1.0001	0.01
10	1	0.9985	0.15
9	1	1.0024	0.24
8	1	0.9974	0.26
7	1	1.0005	0.05
6	1	0.9956	0.44
5	1	0.9860	1.40
4	2	1.7032	14.84
3	2	1.9986	0.07
2	2	1.9420	2.90
1	3	3.0004	0.01

下载: 导出CSV

参考文献(12)

[1]	DUTTON D M, CONROY G V. A review of machine learning[J]. The Knowledge Engineering Review, 1997, 12(4): 341-367. doi: 10.1017/S026988899700101X
[2]	DU X D, CAI Y H, WANG S, et al. Overview of deep learning[C]//Proceedings of the 31st Youth Academic Annual Conference of Chinese Association of Automation (YAC). Wuhan: IEEE, 2016: 159-164.
[3]	JIA Z Y, MA J W, WANG F J, et al. Hybrid of simulated annealing and SVM for hydraulic valve characteristics prediction[J]. Expert Systems with Applications, 2011, 38(7): 8030-8036. doi: 10.1016/j.eswa.2010.12.132
[4]	贾春玉,康凯旋,高伟,等. 基于CNN+LSTM神经网络的电液伺服阀故障预测[J]. 液压与气动,2020(12): 173-181. doi: 10.11832/j.issn.1000-4858.2020.12.027
[5]	肖凯,黎婧,赵梦薇,等. 小型压水堆功率神经网络预测控制研究[J]. 核动力工程,2020, 41(S2): 50-53.
[6]	曾聿赟,刘井泉,杨春振,等. 基于机器学习的小型核反应堆系统状态预测方法[J]. 核动力工程,2018, 39(1): 117-121.
[7]	HUANG H E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995. doi: 10.1098/rspa.1998.0193
[8]	HUANG N E, SHEN Z, LONG S R. A new view of nonlinear water waves: the Hilbert spectrum[J]. Annual Review of Fluid Mechanics, 1999, 31: 417-457. doi: 10.1146/annurev.fluid.31.1.417
[9]	CHEN D S, JAIN R C. A robust backpropagation learning algorithm for function approximation[J]. IEEE Transactions on Neural Networks, 1994, 5(3): 467-479. doi: 10.1109/72.286917
[10]	SADEGHI B H M. A BP-neural network predictor model for plastic injection molding process[J]. Journal of Materials Processing Technology, 2000, 103(3): 411-416. doi: 10.1016/S0924-0136(00)00498-2
[11]	雷亚国. 基于改进Hilbert-Huang变换的机械故障诊断[J]. 机械工程学报,2011, 47(5): 71-77.
[12]	LIU B, RIEMENSCHNEIDER S, XU Y. Gearbox fault diagnosis using empirical mode decomposition and Hilbert spectrum[J]. Mechanical Systems and Signal Processing, 2006, 20(3): 718-734. doi: 10.1016/j.ymssp.2005.02.003