Assessment of LUT-2006 Subcooled CHF Prediction at PWR Conditions with Freon CHF Data
-
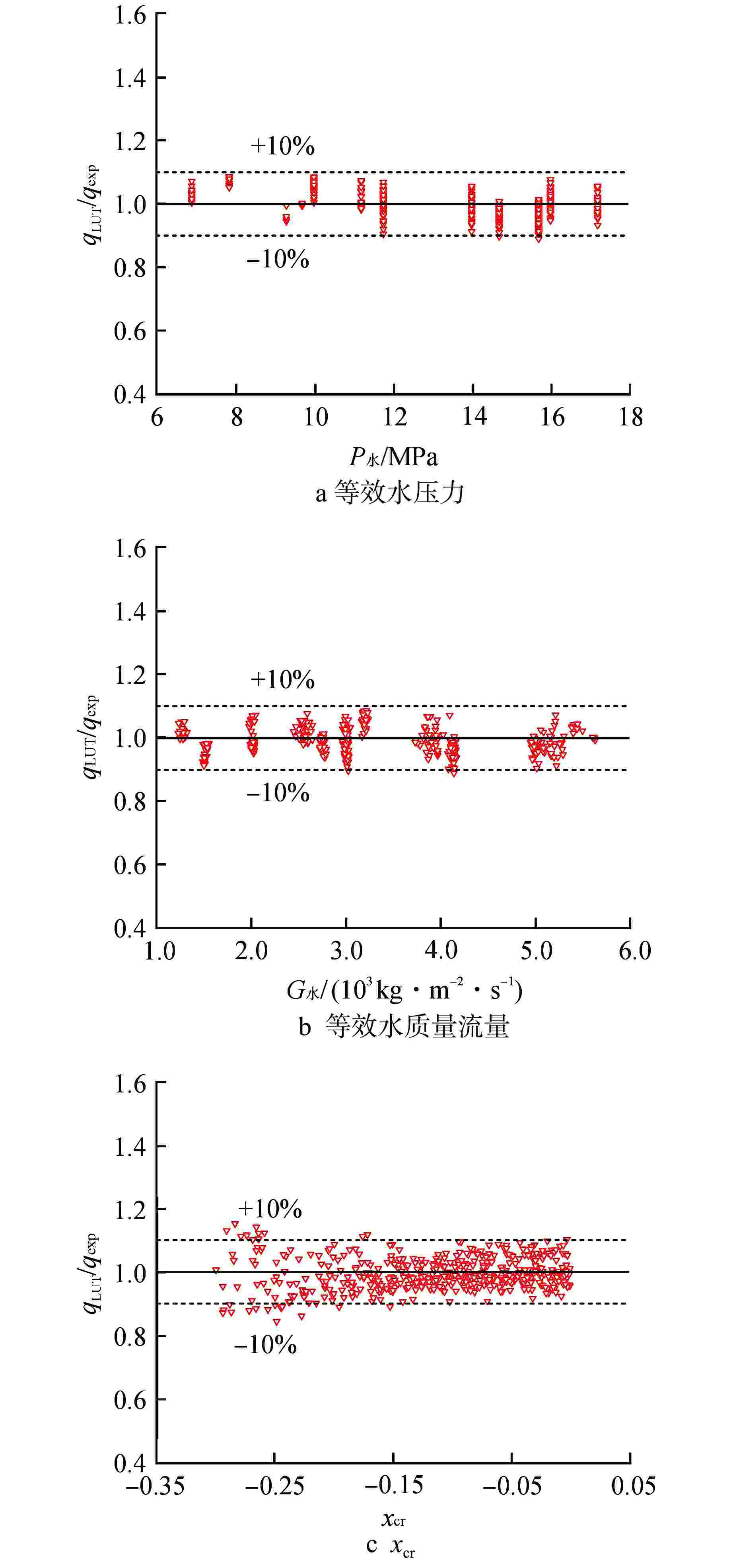
摘要: 以R-134a为模化工质,在内径为8 mm的圆管中进行了临界热流密度(CHF)实验研究。讨论了R-134a的CHF参数变化趋势,评价了Katto的流体模化方法。结果表明,CHF仅受局部参数影响,长径比的影响可以忽略。R-134a的CHF参数趋势与典型水的CHF参数趋势相似。Katto的模化方法在低临界含气率甚至是负临界含气率下都有很高的精度。将R-134a的CHF实验数据通过模化方法转换成等效水数据,并与CHF查询表(LUT)-2006进行了比较。评价结果表明,即使在几乎没有过冷CHF数据的压水堆工况,LUT-2006仍具有很高的预测精度。
-
关键词:
- 临界热流密度(CHF) /
- 氟利昂 /
- 流体模化 /
- CHF查询表(LUT)
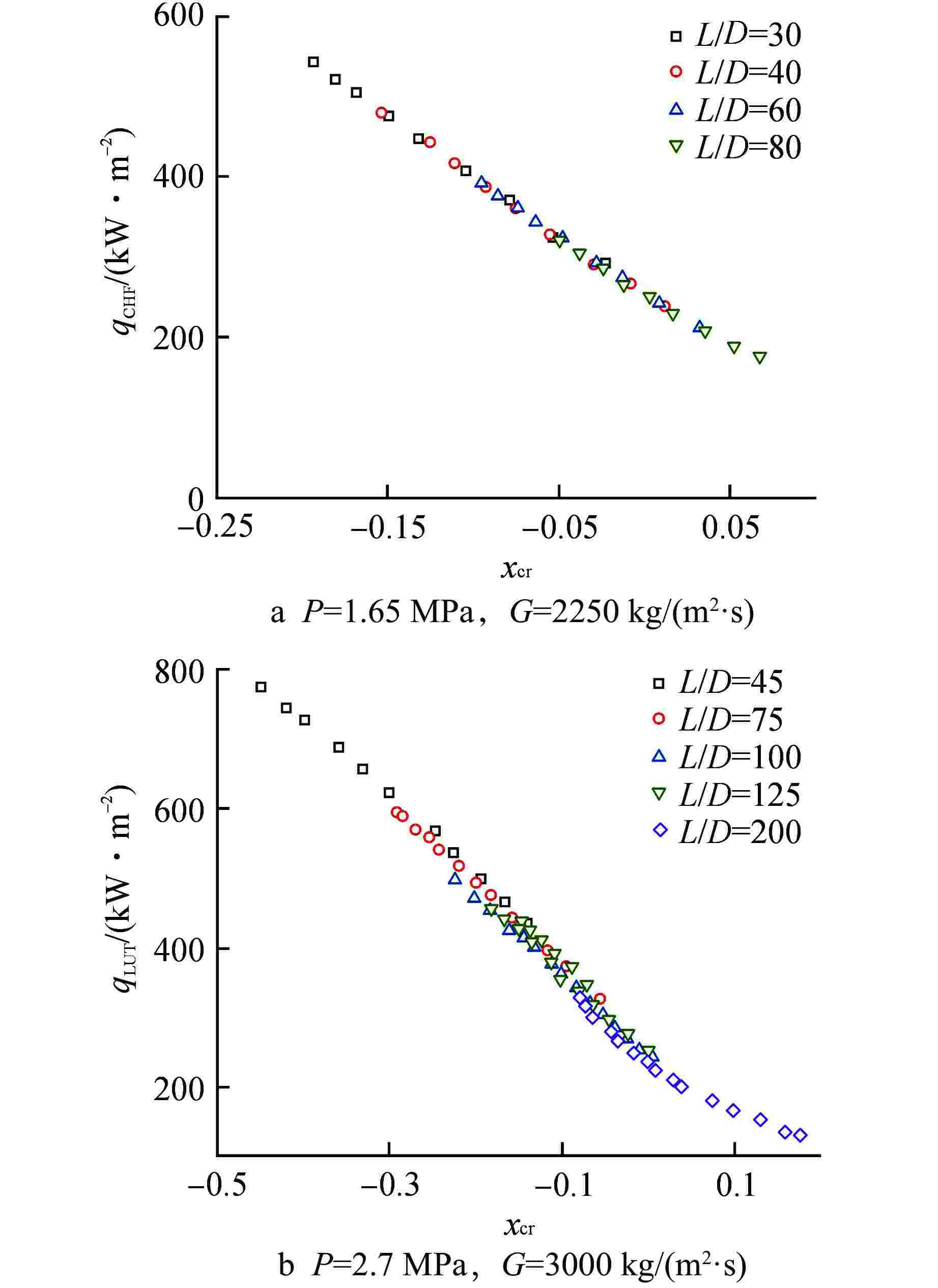
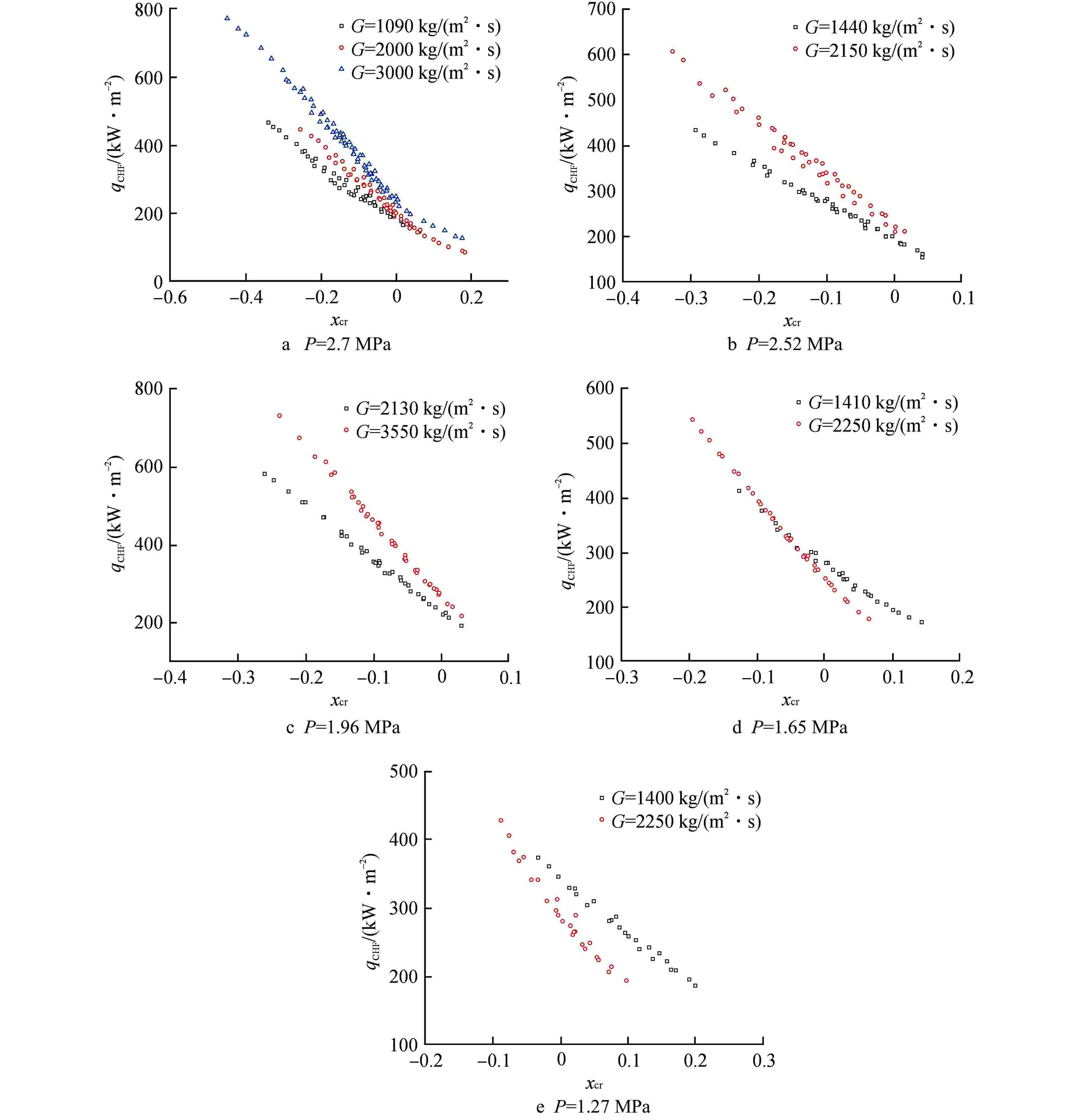
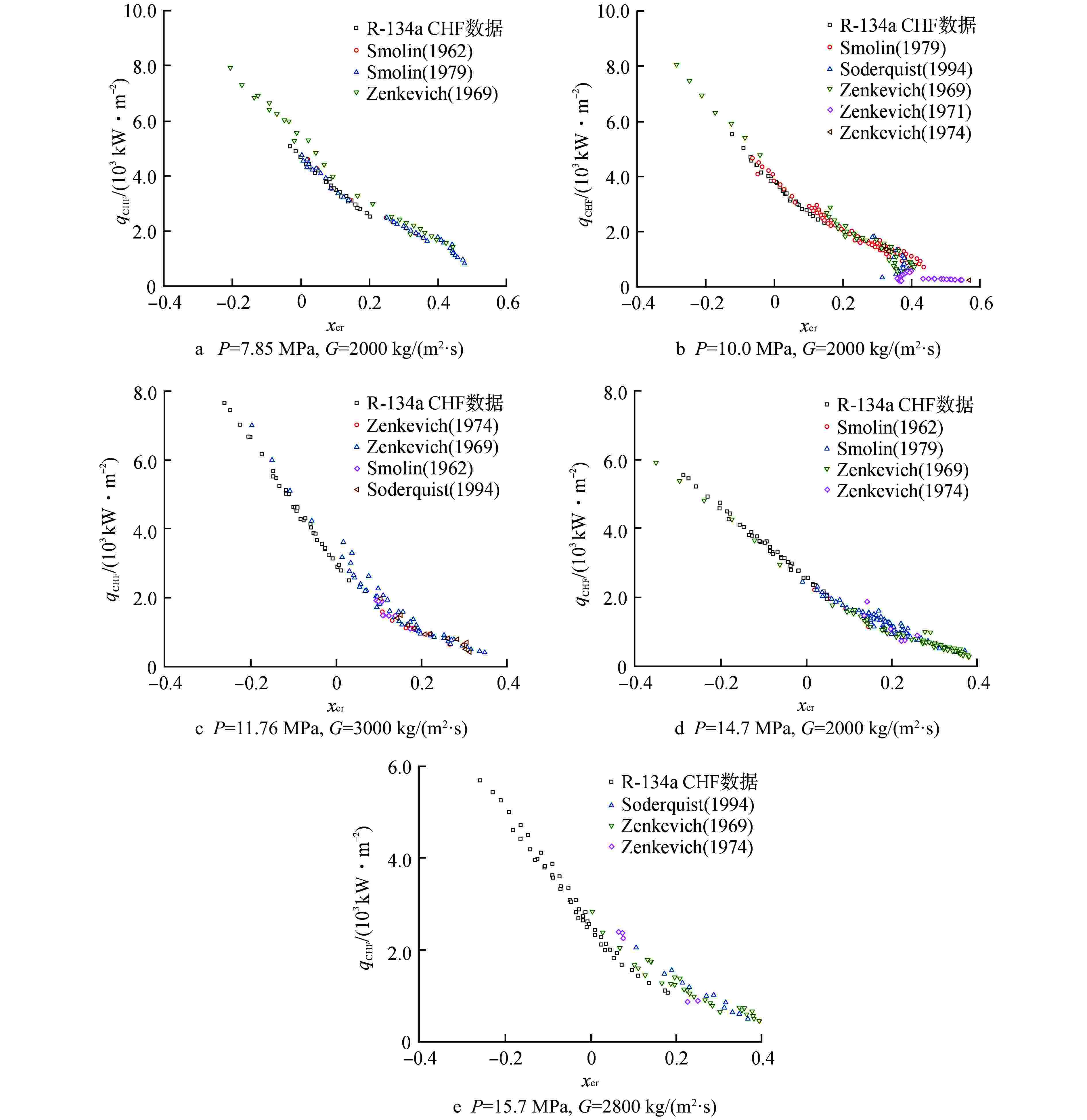
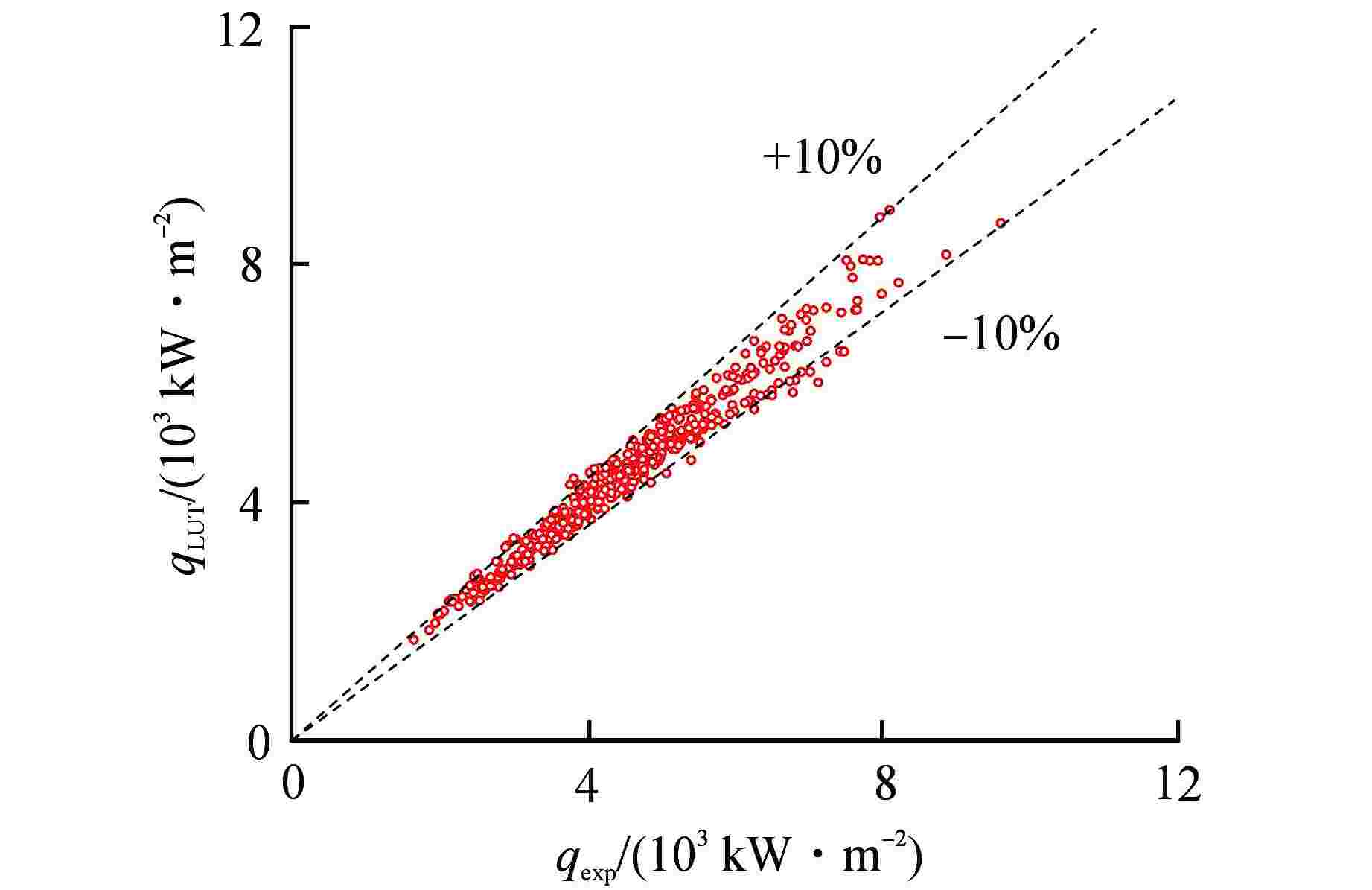
Abstract: An experimental study on the critical heat flux (CHF) is carried out in a circular tube with an inner diameter of 8 mm using R-134a as the modeling working medium. The variation trend of CHF parameters of R-134a is discussed, and Katto’s fluid modeling method is evaluated. The results show that CHF is only affected by local parameters, and the influence of length-diameter ratio can be ignored. The CHF parameter trend of R-134a is similar to that of typical water. Katto's modeling method has high accuracy at low critical air content and even negative critical air content. The CHF experimental data of R-134a are converted into equivalent water data by modeling method and compared with CHF Lookup Table (LUT)-2006. The evaluation results show that LUT-2006 has high prediction accuracy even though there is almost no subcooled CHF data under PWR conditions.-
Key words:
- Critical heat flux (CHF) /
- Freon /
- Fluid-to-fluid modeling /
- CHF Look-up Table (LUT)
-
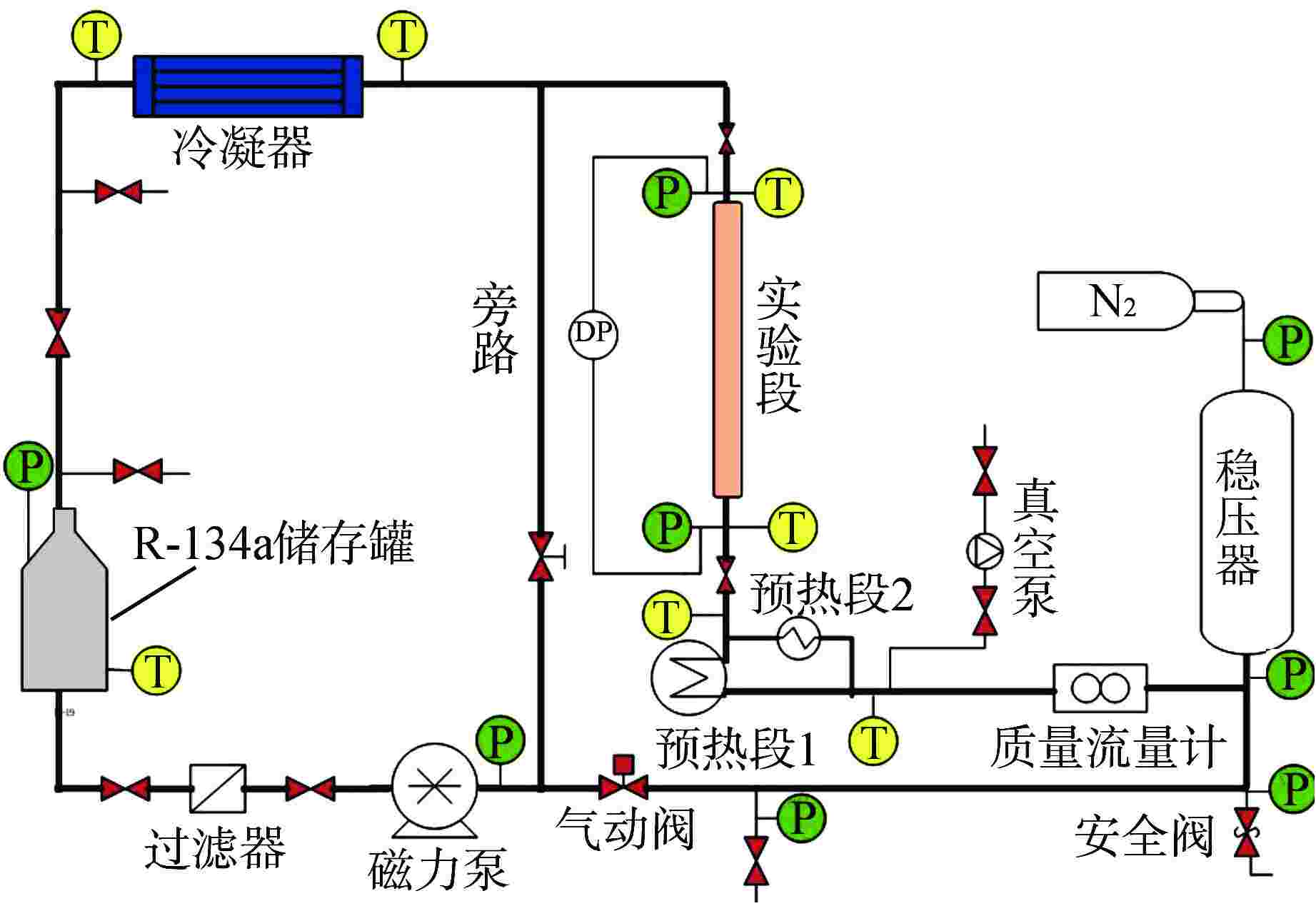
表 1 实验段参数
Table 1. Test Section Parameter
内径/mm 壁厚/mm 总长/m 加热长度/m 材质 8 1 1.6 0.24~1.60 316 不锈钢 表 2 实验工况
Table 2. Experimental Conditions
参数 R-134a 水 压力/MPa 1.27~2.70 7.85~15.70 质量流速/ (kg·m−2·s−1) 1090~3550 1500~5000 进口温度/℃ 20~60 — “—”—无数据 表 3 实验不确定度分析
Table 3. Experiment Uncertainty Analysis
参数 不确定度/% 长度/直径/壁厚 ±0.1/±0.5/±3.0 压力 ±0.7 温度 ±1.3 质量流速 ±1.7 电压 ±0.2 电流 ±0.2 功率 ±2.2 热流密度 ±5.1 表 4 Katto模化方法
Table 4. Katto’s Fluid-to-fluid Modeling Method
类型 无量纲数 几何相似 $ {\left( {\dfrac{L}{D}} \right)_{\text{R}}} = {\left( {\dfrac{L}{D}} \right)_{\text{w}}} $ 水力学相似 $ {\left( {\dfrac{{{\rho _{\text{l}}}}}{{{\rho _{\text{g}}}}}} \right)_{\text{R}}} = {\left( {\dfrac{{{\rho _{\text{l}}}}}{{{\rho _{\text{g}}}}}} \right)_{\text{w}}} $ 热力学相似 $ {\left( {\dfrac{{\Delta h}}{{{h_{{\text{fg}}}}}}} \right)_{\text{R}}} = {\left( {\dfrac{{\Delta h}}{{{h_{{\text{fg}}}}}}} \right)_{\text{w}}} 或 {\left( {{x_{{\text{cr}}}}} \right)_{\text{R}}} = {\left( {{x_{{\text{cr}}}}} \right)_{\text{w}}} $ We相同 $ W{e_{\text{R}}} = W{e_{\text{w}}} $ R—R-134a;w—水;We—韦伯数,$ We = {{\left( {G\sqrt D } \right)} \mathord{\left/ {\vphantom {{\left( {G\sqrt D } \right)} {\sqrt {{\rho _{\text{l}}}\sigma } }}} \right. } {\sqrt {{\rho _{\text{l}}}\sigma } }} $ 表 5 压水堆工况下过冷氟利昂CHF数据库
Table 5. Subcooled Freon CHF Database under PWR Condition
-
[1] KATTO Y, OHNO H. An improved version of the generalized correlation of critical heat flux for the forced convective boiling in uniformly heated vertical tubes[J]. International Journal of Heat and Mass Transfer, 1984, 27(9): 1641-1648. doi: 10.1016/0017-9310(84)90276-X [2] BOWRING R W. Simple but accurate round tube, uniform heat flux, dryout correlation over the pressure range 0.7 to 17 MN/m2 (100 to 2500 psia), AEEW-R-789[R]. Winfrith: Atomic Energy Establishment, 1972. [3] HALL D D, MUDAWAR I. Critical heat flux (CHF) for water flow in tubes—II. : subcooled CHF correlations[J]. International Journal of Heat and Mass Transfer, 2000, 43(14): 2605-2640. doi: 10.1016/S0017-9310(99)00192-1 [4] SHAH M M. A generalized graphical method for predicting chf in uniformly heated vertical tubes[J]. International Journal of Heat and Mass Transfer, 1979, 22(4): 557-568. doi: 10.1016/0017-9310(79)90059-0 [5] LEE C H, MUDAWWAR I. A mechanistic critical heat flux model for subcooled flow boiling based on local bulk flow conditions[J]. International Journal of Multiphase Flow, 1988, 14(6): 711-728. doi: 10.1016/0301-9322(88)90070-5 [6] HARAMURA Y, KATTO Y. A new hydrodynamic model of critical heat flux, applicable widely to both pool and forced convection boiling on submerged bodies in saturated liquids[J]. International Journal of Heat and Mass Transfer, 1983, 26(3): 389-399. doi: 10.1016/0017-9310(83)90043-1 [7] WEISMAN J, PEI B S. Prediction of critical heat flux in flow boiling at low qualities[J]. International Journal of Heat and Mass Transfer, 1983, 26(10): 1463-1477. doi: 10.1016/S0017-9310(83)80047-7 [8] LEVY S, HEALZER J M, ABDOLLAHIAN D. Prediction of critical heat flux in vertical pipe flow[J]. Nuclear Engineering and Design, 1981, 65(1): 131-140. doi: 10.1016/0029-5493(81)90126-6 [9] GROENEVELD D C, SHAN J Q, VASIĆ A Z, et al. The 2006 CHF look-up table[J]. Nuclear Engineering and Design, 2007, 237(15-17): 1909-1922. doi: 10.1016/j.nucengdes.2007.02.014 [10] TONG L S. Thermal analysis of pressurized water reactors[J]. Nuclear Science and Engineering, 1972, 48(2): 233. doi: 10.13182/NSE72-A22480 [11] MOTLEY F E, HILL K W, CADEK F F, et al. New Westinghouse correlation WRB-1 for predicting critical heat flux in rod bundles with mixing vane grids: WCAP-8763[R]. Pittsburgh: Westinghouse Electric Corp. , 1976. [12] STEVENS G F. A quantitative comparison between burnout data for water at 1000lb/in2 and freon 12 at 155lb/in2 uniformly heated round tubes vertical upwards: AEWW-R-327[R]. Winfrith: Atomic Energy Establishment, 1964. [13] AHMAD S Y. Fluid to fluid modeling of critical heat flux: a compensated distortion model[J]. International Journal of Heat and Mass Transfer, 1973, 16(3): 641-662. doi: 10.1016/0017-9310(73)90229-9 [14] KATTO Y. A generalized correlation of critical heat flux for the forced convection boiling in vertical uniformly heated round tubes—a supplementary report[J]. International Journal of Heat and Mass Transfer, 1979, 22(6): 783-794. doi: 10.1016/0017-9310(79)90017-6 [15] PIORO I L, GROENEVELD D C, CHENG S C, et al. Comparison of CHF measurements in R-134a cooled tubes and the water CHF look-up table[J]. International Journal of Heat and Mass Transfer, 2001, 44(1): 73-88. doi: 10.1016/S0017-9310(00)00093-4 [16] CHUN S Y, HONG S D, CHO Y S, et al. Comparison of the CHF data for water and refrigerant HFC-134a by using the fluid-to-fluid modeling methods[J]. International Journal of Heat and Mass Transfer, 2007, 50(21-22): 4446-4456. doi: 10.1016/j.ijheatmasstransfer.2005.06.039 [17] TAIN R M, CHENG S C, GROENEVELD D C. Critical heat flux measurements in a round tube for CFCs and CFC alternatives[J]. International Journal of Heat and Mass Transfer, 1993, 36(8): 3039-2049. doi: 10.1016/S0017-9310(05)80135-8 [18] AKHTAR S W, MOON S K, CHUN S Y, et al. Modeling capability of R134a for a critical heat flux of water in a vertical 5 × 5 rod bundle geometry[J]. International Journal of Heat and Mass Transfer, 2006, 49(7-8): 1299-1309. doi: 10.1016/j.ijheatmasstransfer.2005.10.019 [19] CHENG X. Experimental investigations on critical heat flux in 8 mm tubes and in 7-rod bundles: KfK-Report 4884[R]. German: Research Center Karlsruhe, 1991. (in German) [20] DOERFFER S, GROENEVELD D C, CHENG S C. A comparison of critical heat flux in tubes and bilaterally heated annuli[J]. Nuclear Engineering and Design, 1997, 177(1-3): 105-120. doi: 10.1016/S0029-5493(97)00188-X [21] KATTO Y, YOKOYA S, MIAKE S, et al. Critical heat flux on a uniformly heated cylinder in a cross flow of saturated liquid over a very wide range of vapor-to-liquid density ratio[J]. International Journal of Heat and Mass Transfer, 1987, 30(9): 1971-1977. doi: 10.1016/0017-9310(87)90255-9 [22] GROENEVELD D C. On the definition of critical heat flux margin[J]. Nuclear Engineering and Design, 1996, 163(1-2): 245-247. doi: 10.1016/0029-5493(95)01173-0 -





 下载:
下载: