Calculation of Stress Intensity Factor of External Surface Crack on the Nozzle of Steam Generator in Nuclear Power Plant
-
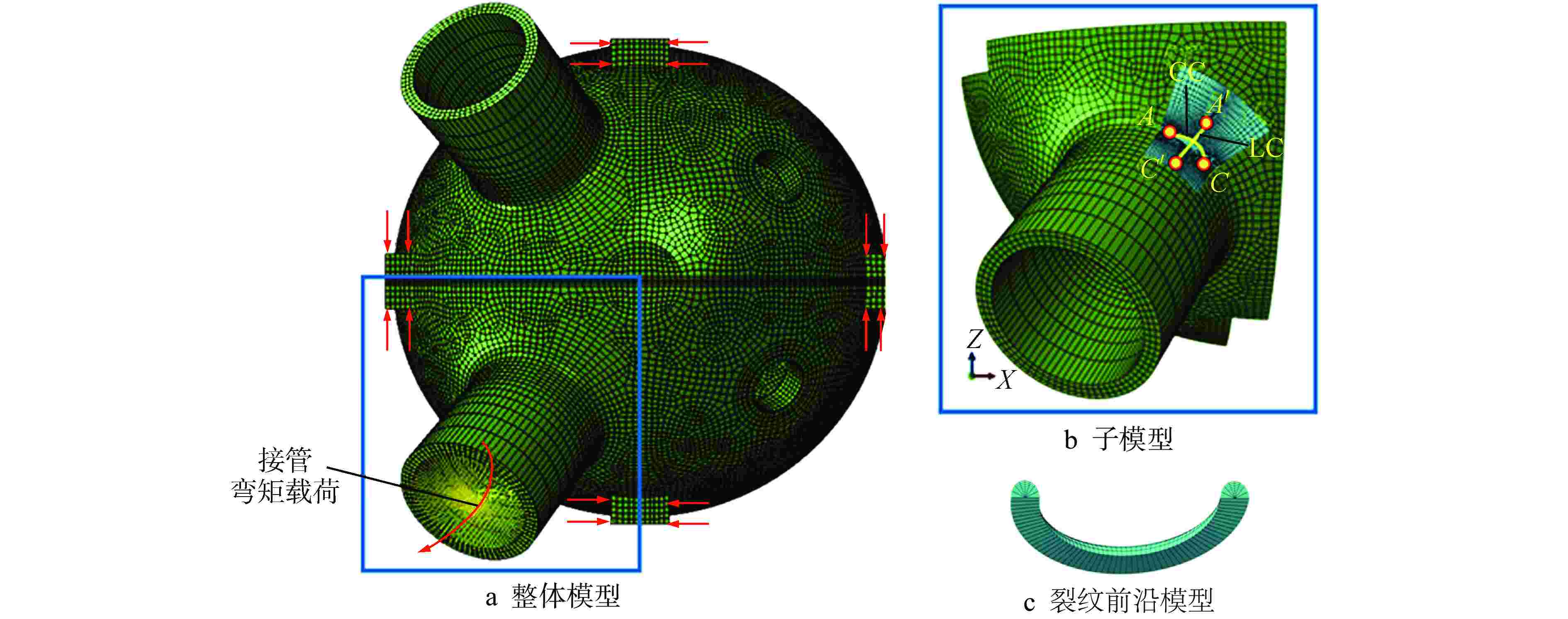
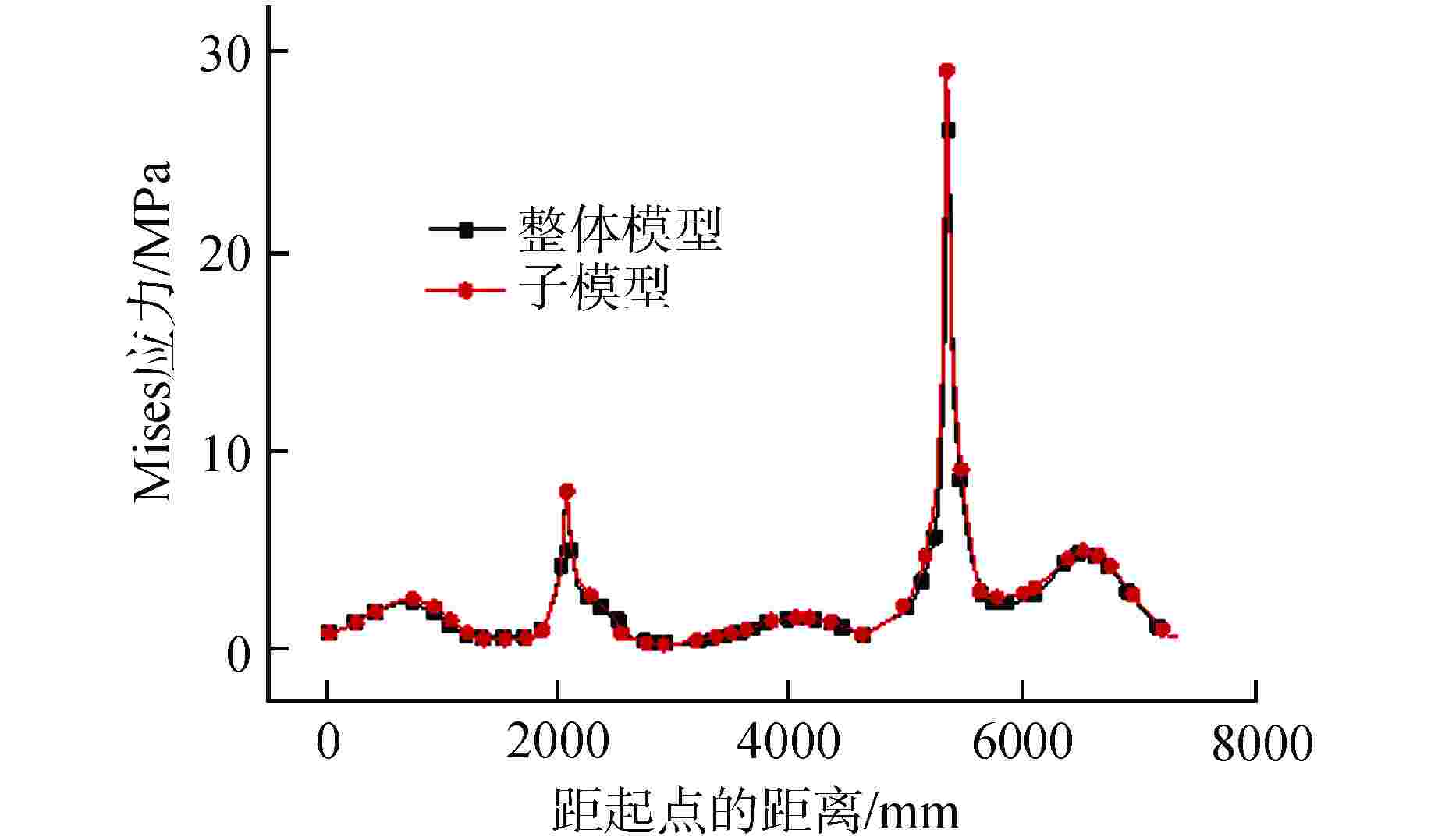
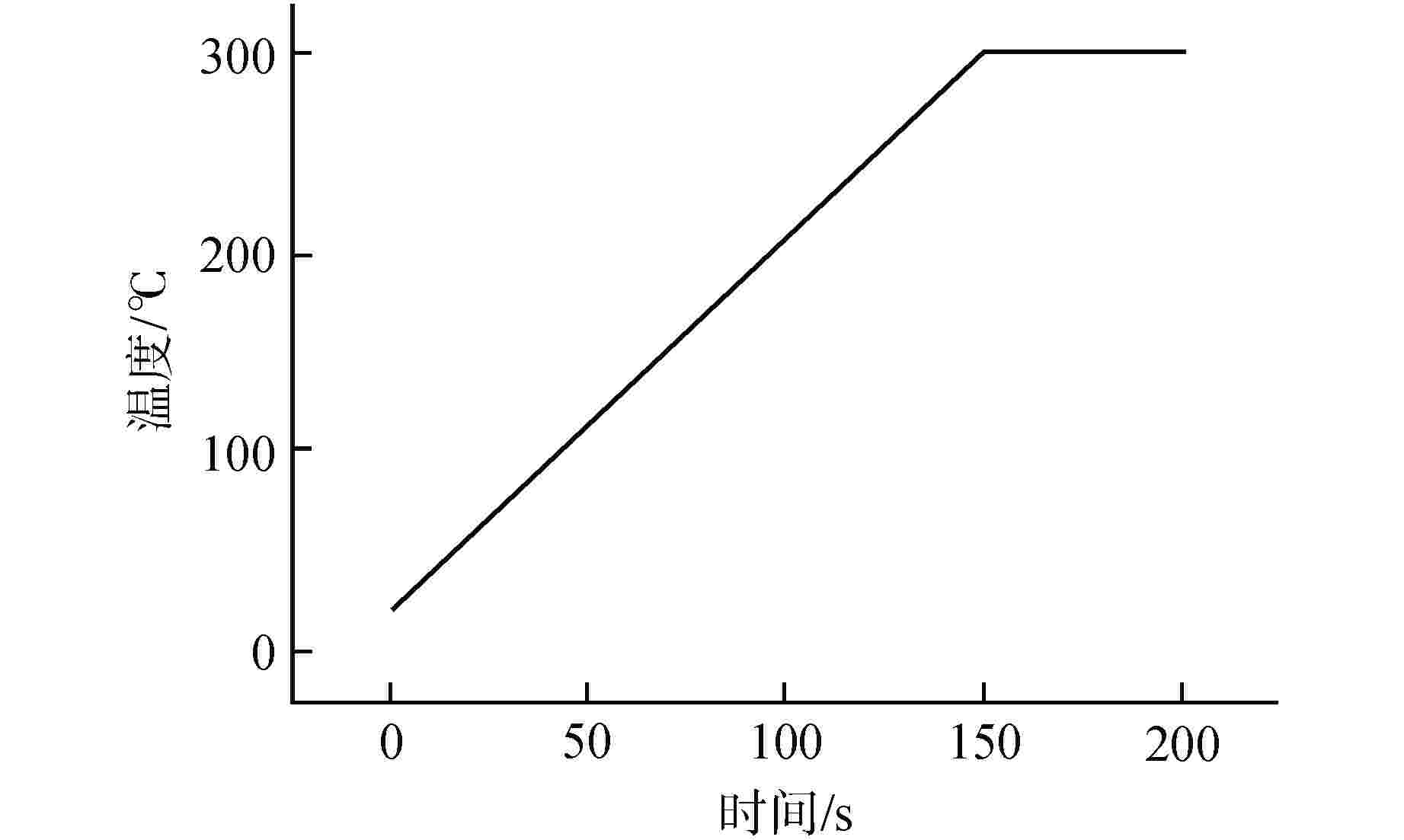
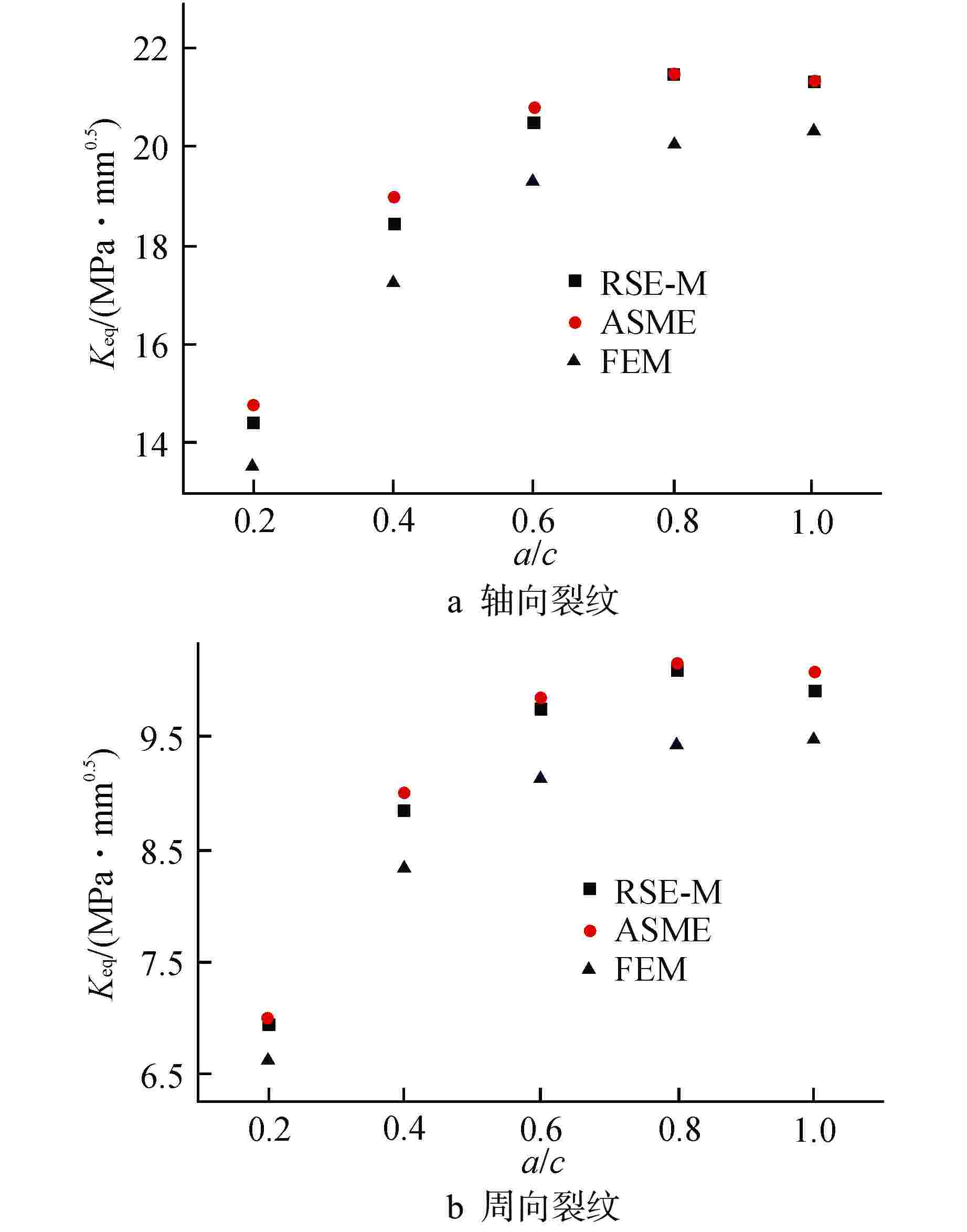
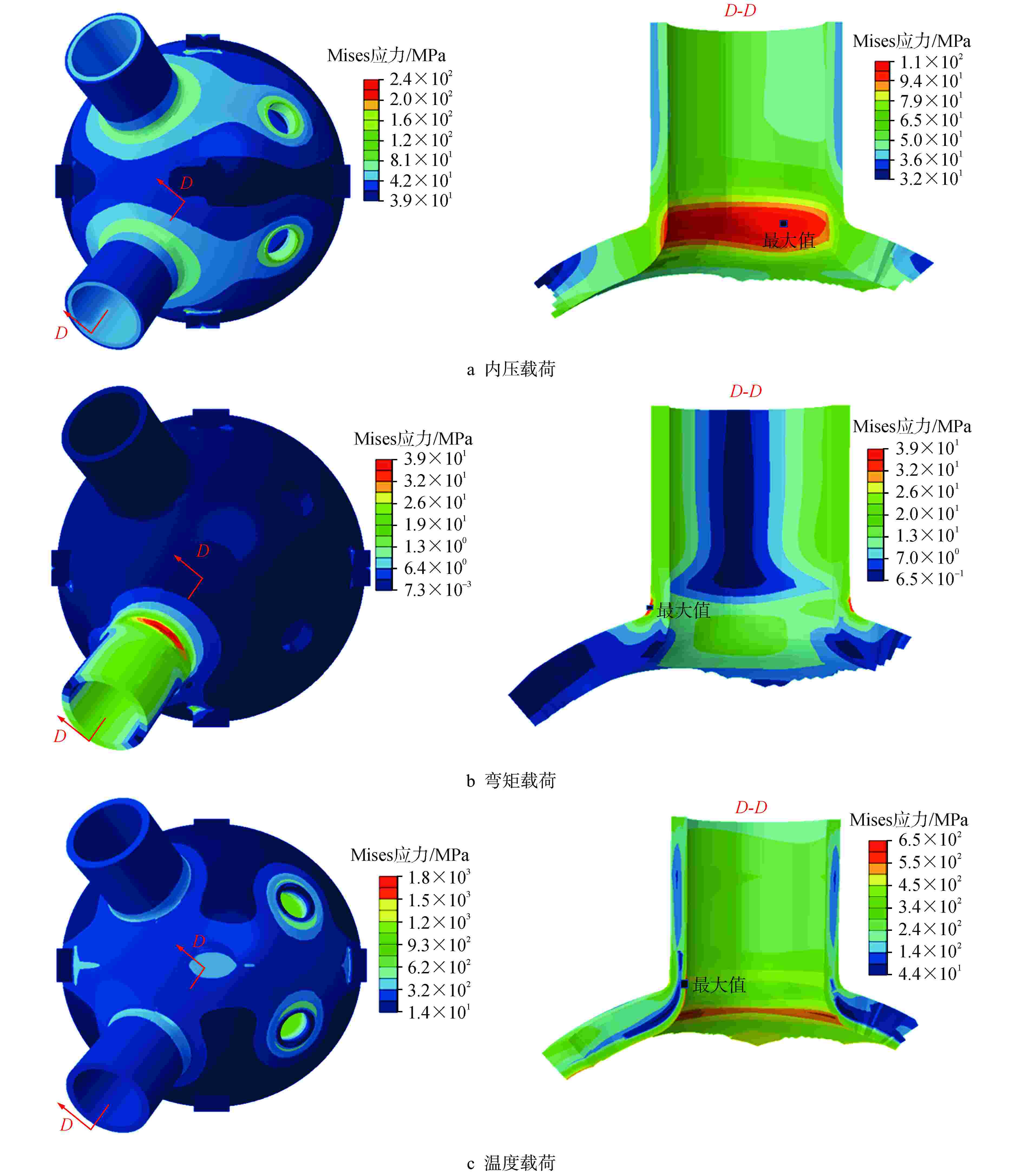
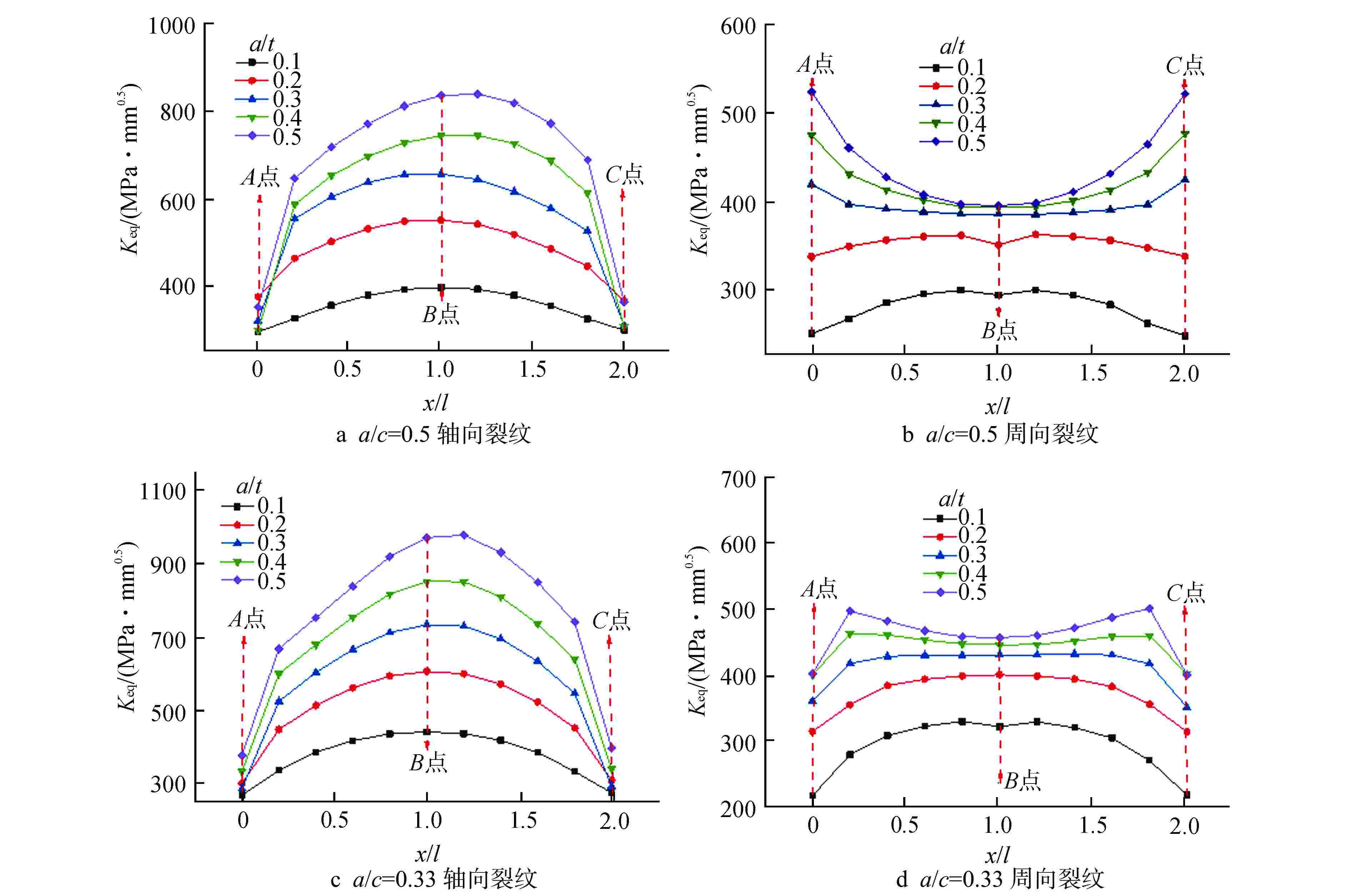
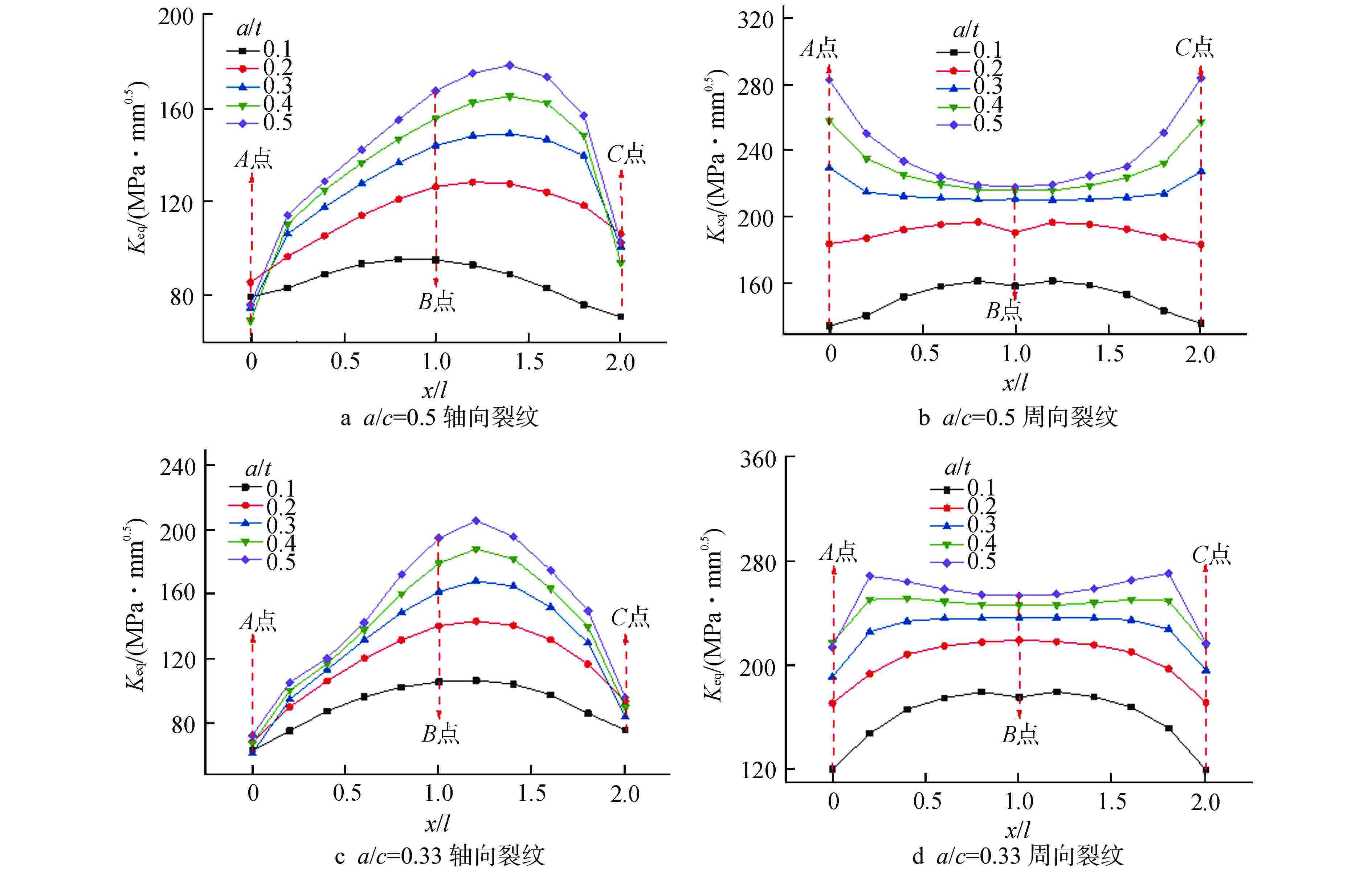
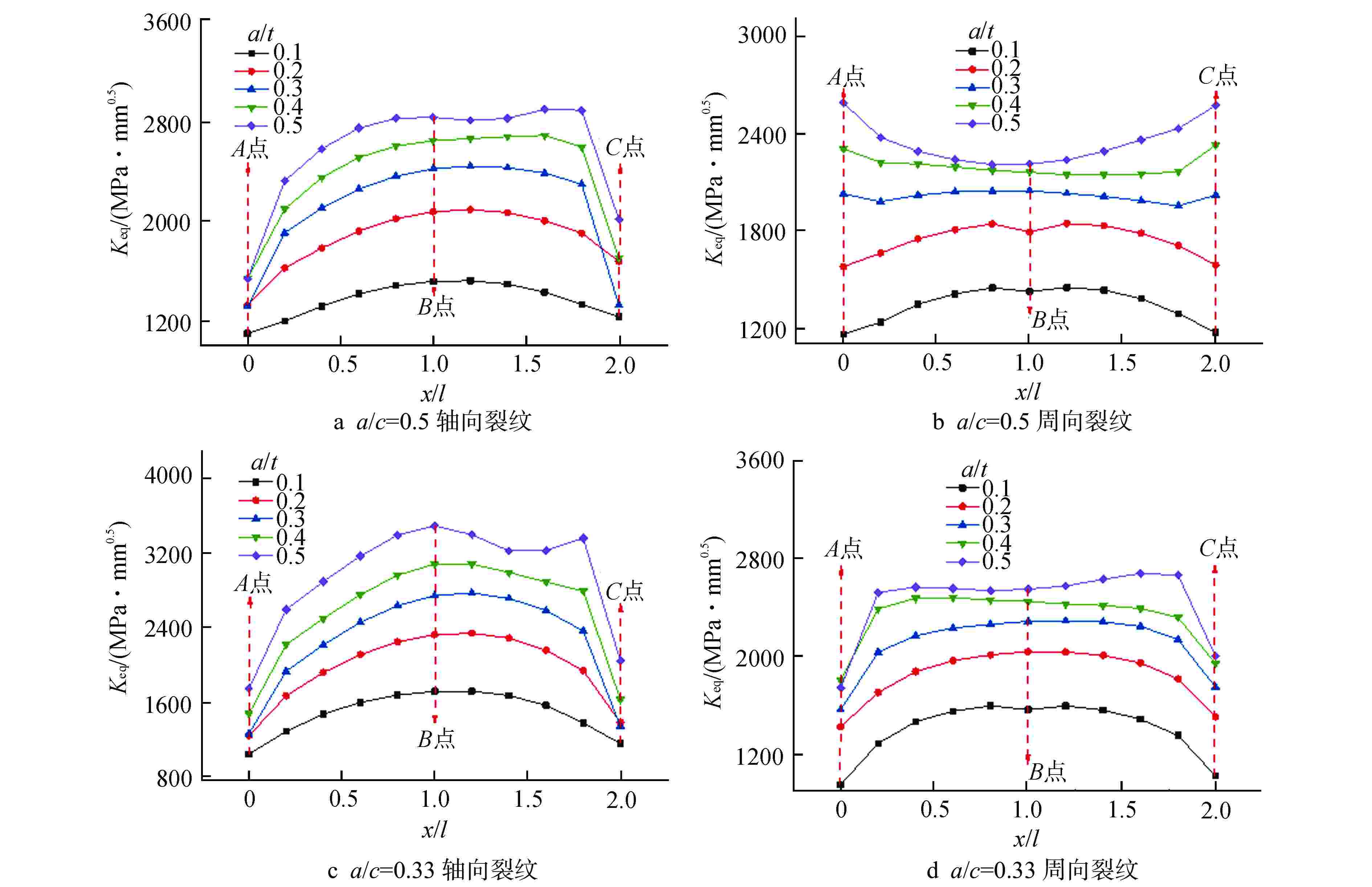
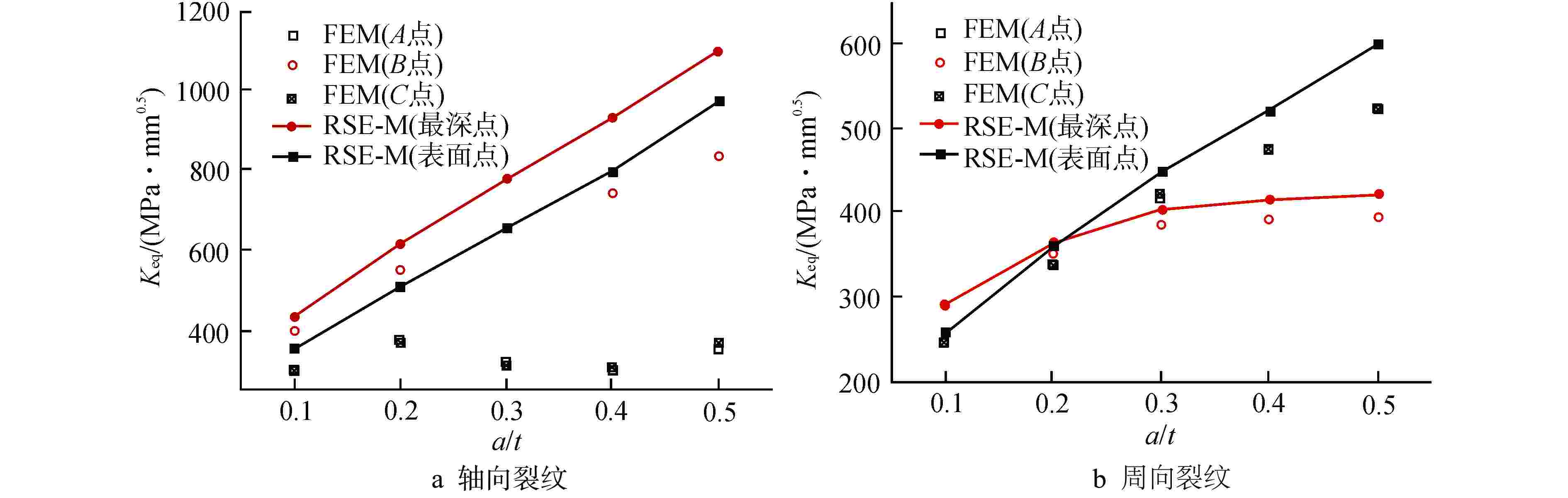
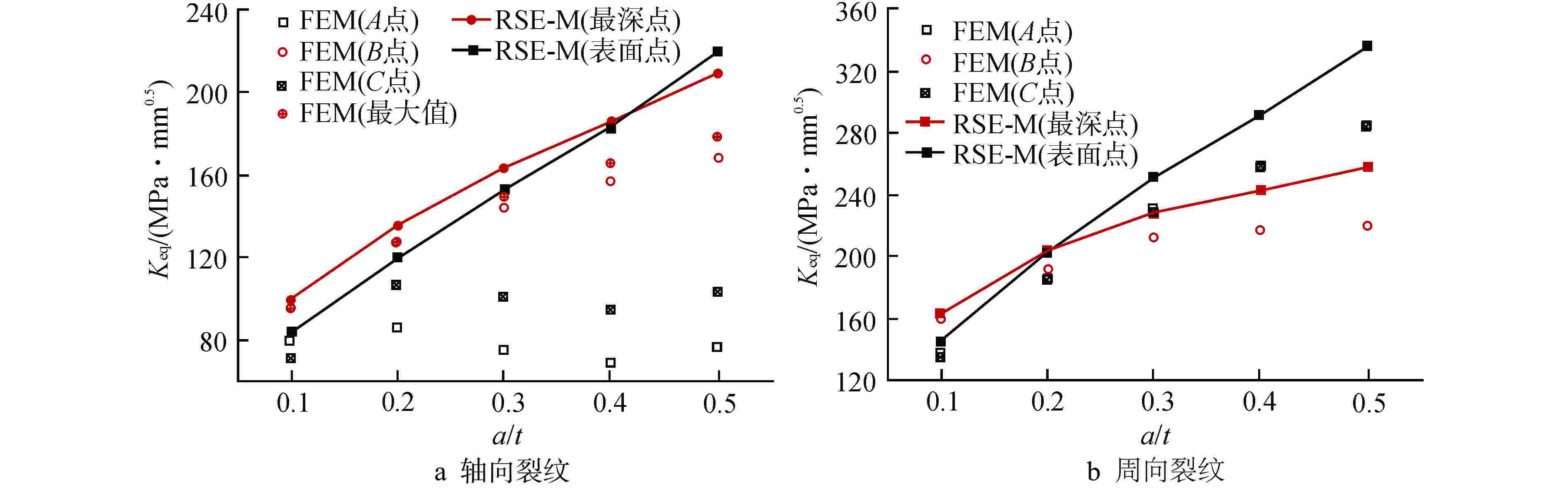
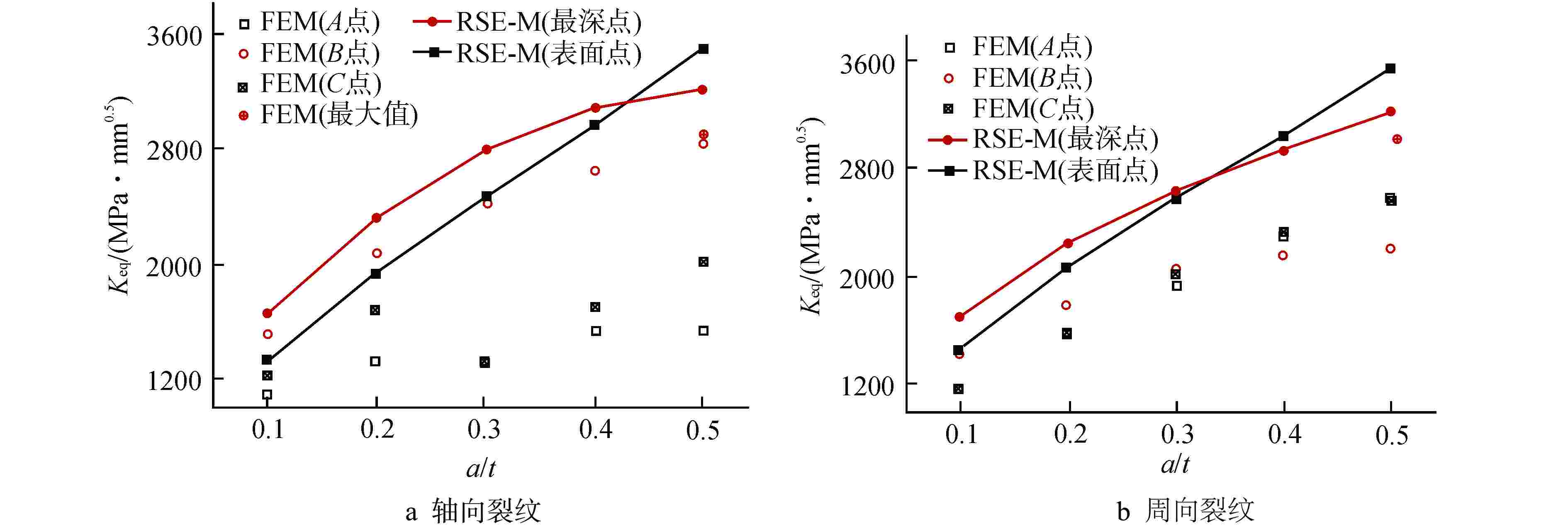
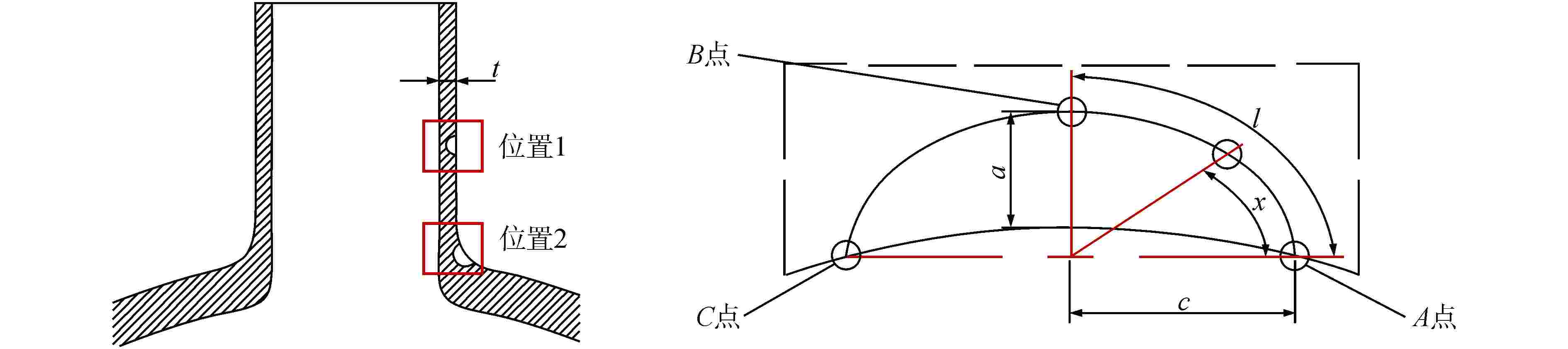
摘要: 核电蒸汽发生器（SG）接管嘴处由于其结构的特殊性，易在制造及服役过程中产生缺陷。为评价该处缺陷的安全性，需要工程可用的应力强度因子解。本文以核电SG接管嘴外表面裂纹为研究对象，采用有限元方法（FEM）及RSE-M规范计算获得了不同方向及尺寸裂纹在内压、弯矩和温度载荷下的等效应力强度因子值，并分析了不同载荷作用下等效应力强度因子在裂纹前沿的分布规律。将计算结果与RSE-M规范的直管应力强度因子解进行比较，发现RSE-M规范的直管应力强度因子计算方法可保守地应用于SG接管嘴处裂纹，并且随着裂纹深度的增加保守度增大。为实现SG接管嘴处缺陷安全的准确评价，基于有限元计算和RSE-M影响系数法给出了适用于SG接管嘴外表面裂纹的应力强度因子计算方法，该方法可以为SG的设计与维护提供指导。
-
关键词:
- 应力强度因子 /
- 蒸汽发生器（SG） /
- 接管嘴 /
- RSE-M规范 /
- 有限元方法（FEM）
Abstract: Due to the particularity of its structure, the nozzle of the nuclear steam generator (SG) is prone to defects during manufacturing and operating process. In order to evaluate the safety of the defect, the stress intensity factor solution available in engineering is required. In this paper, taking the external surface crack of nuclear SG nozzle as the research object, the equivalent stress intensity factors of cracks in different directions and sizes under internal pressure, bending moment and temperature loads are calculated by finite element method and RSE-M code, and the distribution law of equivalent stress intensity factors at the crack front under different loads is analyzed. By comparing the calculation results with the straight pipe stress intensity factor solution of RSE-M code, it is found that the straight pipe stress intensity factor calculation method of RSE-M code can be conservatively applied to the cracks at SG nozzle, and the conservation increases with increasing crack depth. In order to realize the accurate evaluation of the defect safety of SG nozzle, a calculation method of stress intensity factor applicable to the cracks on the external surface of SG nozzle is given based on finite element calculation and RSE-M influence coefficient method, which can provide guidance for the design and maintenance of SG nozzle.-
Key words:
- Stress intensity factor /
- Steam generator(SG) /
- Nozzle /
- RSE-M code /
- Finite element method (FEM)
-
图 1 SG接管嘴处裂纹位置及裂纹尺寸示意图
B点—裂纹最深点；A点、C点—裂纹表面点；t—筒体壁厚；a—绝对裂纹深度；c—裂纹半宽度；x—裂纹前沿任一点到表面点A沿着裂纹前沿的距离；l—裂纹前沿半长度
Figure 1. Schematic Diagram of Crack Location and Crack Size at Nozzle of SG
图 5 内压下直管裂纹前沿最深点Keq
a/c—形状比
Figure 5. Keq of Deepest Point on the Straight Pipe under Internal Pressure
图 7 内压载荷下Keq沿裂纹前沿的分布
Figure 7. Distribution of Keq Along Crack Front under Internal Pressure Load
图 8 弯矩载荷下Keq沿裂纹前沿的分布
Figure 8. Distribution of Keq Along Crack Front under Bending Moment Load
图 9 温度载荷下Keq沿裂纹前沿的分布
Figure 9. Distribution of Keq Along Crack Front under Temperature Load
图 10 内压载荷下FEM和RSE-M的Keq对比
Figure 10. Comparison between Keq Calculated by FEM and RSE-M under Internal Pressure Load
图 11 弯矩载荷下FEM和RSE-M的Keq对比
Figure 11. Comparison between Keq Calculated by FEM and RSE-M under Bending Moment Load
图 12 温度载荷下下FEM和RSE-M的Keq对比
Figure 12. Comparison between Keq Calculated by FEM and RSE-M under Thermal Load
表 1 16MND5性能参数
Table 1. Performance Parameters of 16MND5
温度/
℃泊松比 密度/
(kg·m−3)弹性模
量/GPa热导率/
[W·(m·℃)−1]膨胀系
数/10−6℃−120 0.3 7850 204 37.7 11.2 50 203 38.6 11.5 100 200 39.9 11.8 150 197 40.5 12.1 200 193 40.5 12.5 250 189 40.2 12.8 300 185 39.5 13.1 350 180 38.7 13.4 
下载: 导出CSV
-
[1] AFCEN. RSE-M: in-service inspection rules for mechanical components of PWR nuclear islands[M]. Paris: French Association for Design, Construction and In-Service Inspection Rules for Nuclear Island Components, 2010. [2] ASME. Rules for construction of pressure vessels, Division 3, Alternative rules for construction of high pressure vessels: ASME BPVC VIII-3[S]. New York: The American Society of Mechanical Engineering, 2010. [3] NEWMAN JR J C, RAJU I S. Stress-intensity factors for internal surface cracks in cylindrical pressure vessels[J]. Journal of Pressure Vessel Technology, 1980, 102(4): 342-346. doi: 10.1115/1.3263343 [4] NEWMAN J C, RAJU I S. Stress-intensity factor equations for cracks in three-dimensional finite bodies[M]. Philadelphia: ASTM Special Technical Publication, 1983: 238-265. [5] ISMAIL A E, ARIFFIN A K, ABDULLAH S, et al. Stress intensity factors for surface cracks in round bar under single and combined loadings[J]. Meccanica, 2012, 47(5): 1141-1156. doi: 10.1007/s11012-011-9500-7 [6] DIAMANTOUDIS A T, LABEAS G N. Stress intensity factors of semi-elliptical surface cracks in pressure vessels by global-local finite element methodology[J]. Engineering Fracture Mechanics, 2005, 72(9): 1299-1312. doi: 10.1016/j.engfracmech.2004.10.004 [7] CHAPULIOT S. Stress intensity factor calculation in sharp and beveled edge nozzle corners[J]. International Journal of Pressure Vessels and Piping, 2016, 141: 11-18. doi: 10.1016/j.ijpvp.2016.03.015 [8] LI Y B, JIN T, WANG Z H, et al. Engineering critical assessment of RPV with nozzle corner cracks under pressurized thermal shocks[J]. Nuclear Engineering and Technology, 2020, 52(11): 2638-2651. doi: 10.1016/j.net.2020.04.019 [9] 王大胜,刘攀,熊光明. 考虑接管载荷的反应堆压力容器接管嘴断裂力学分析[J]. 核动力工程,2015, 36(5): 120-123. [10] 张丽屏,苏东川,高世卿,等. 反应堆压力容器接管嘴内隅角应力强度因子计算研究[J]. 原子能科学技术,2017, 51(11): 2042-2048. doi: 10.7538/yzk.2017.youxian.0275 [11] 李东方,杨海波,毛朝晖,等. 热交换管内壁子午面半椭圆裂纹应力强度因子数值计算[J]. 机电工程,2020, 37(3): 253-258. [12] 张兴田. 基于RSE-M规范核电厂反应堆压力容器堆焊层缺陷的断裂力学分析与评定[J]. 机械工程材料,2016, 40(12): 32-36,82. doi: 10.11973/jxgccl201612008 -
计量
- 文章访问数: 180
- HTML全文浏览量: 37
- PDF下载量: 49
- 被引次数: 0
