Research on Calculation Method of Containment Spray Coverage Rate Based on Monte Carlo Simulation Method
-
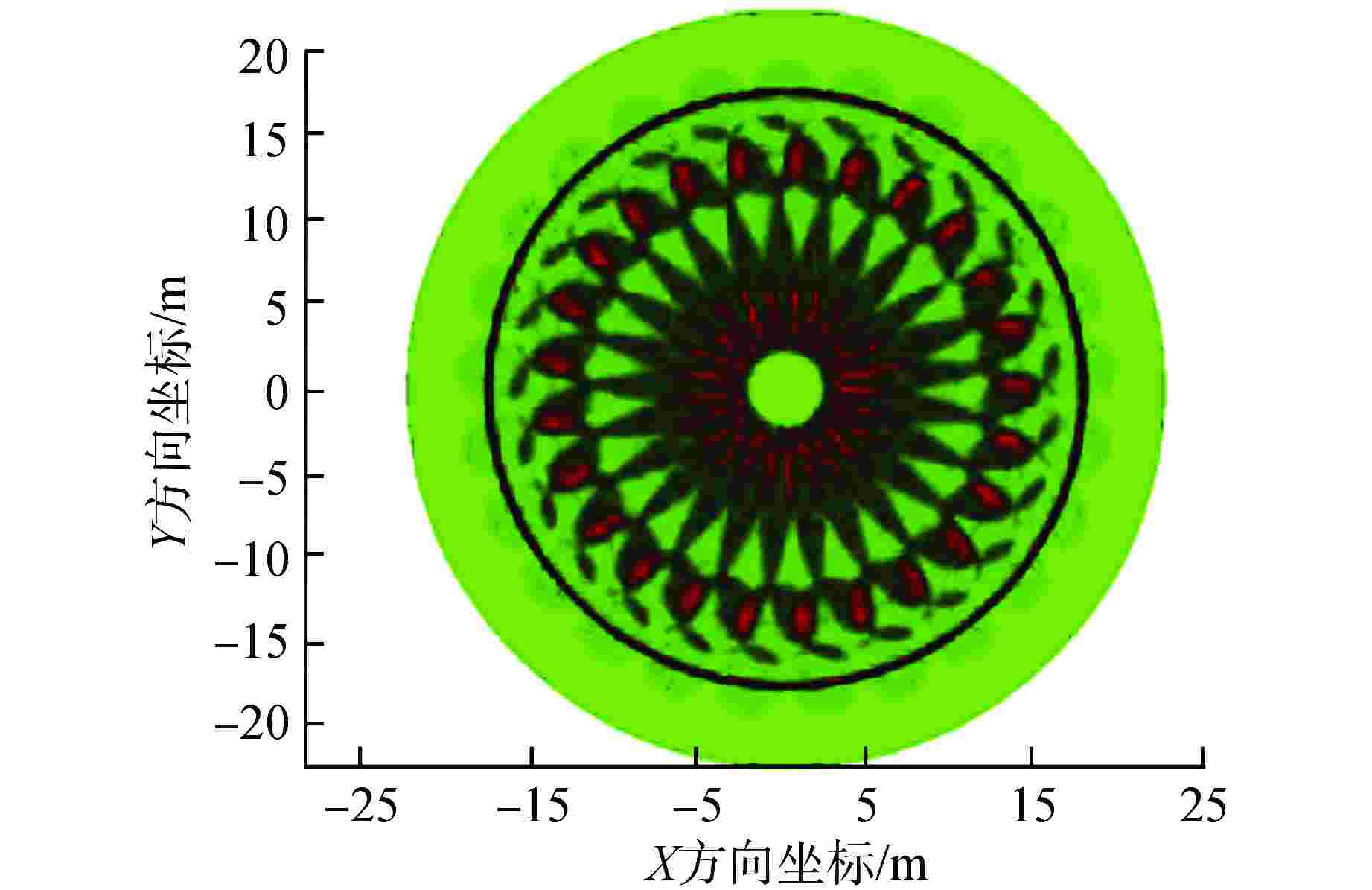
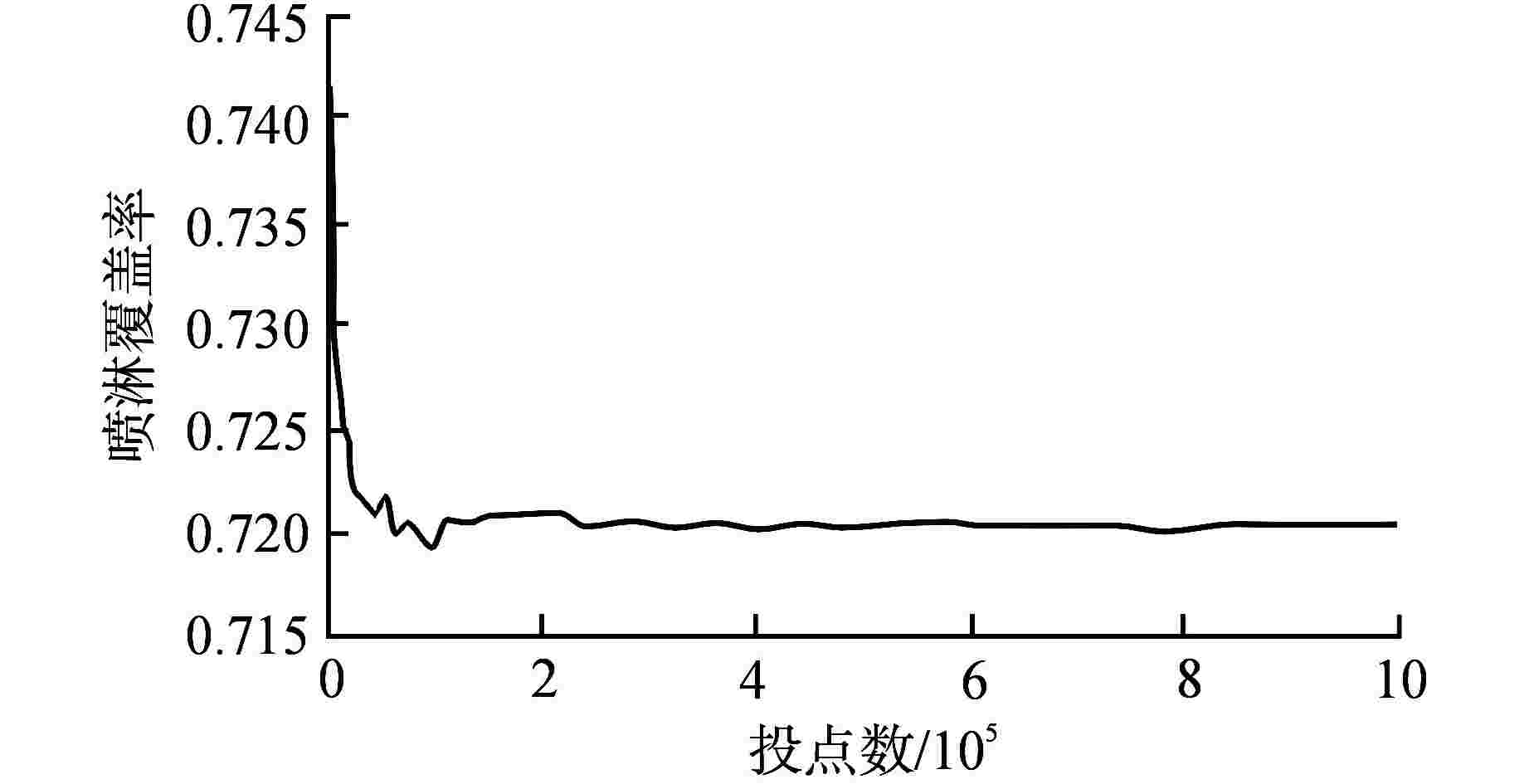
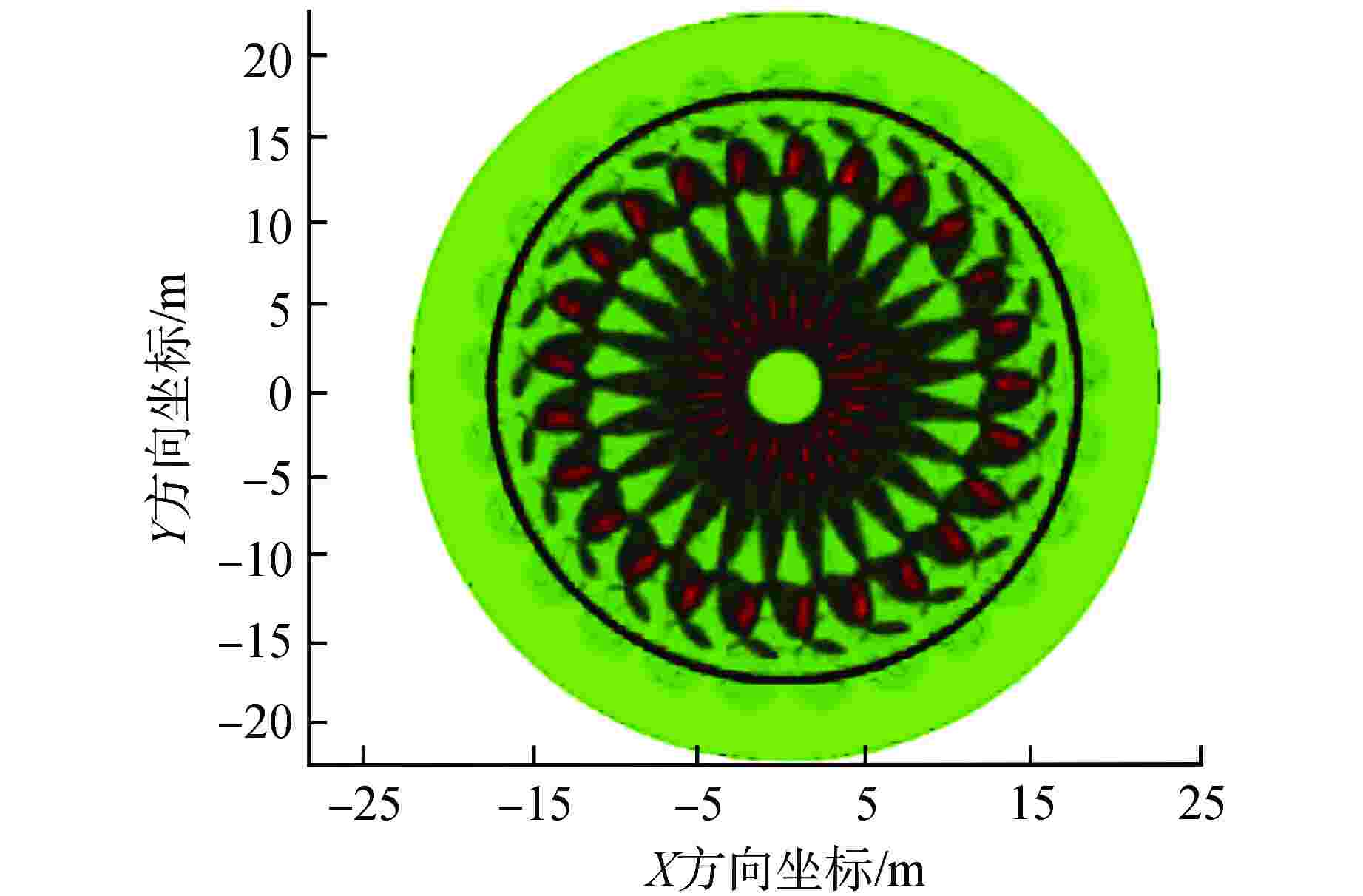
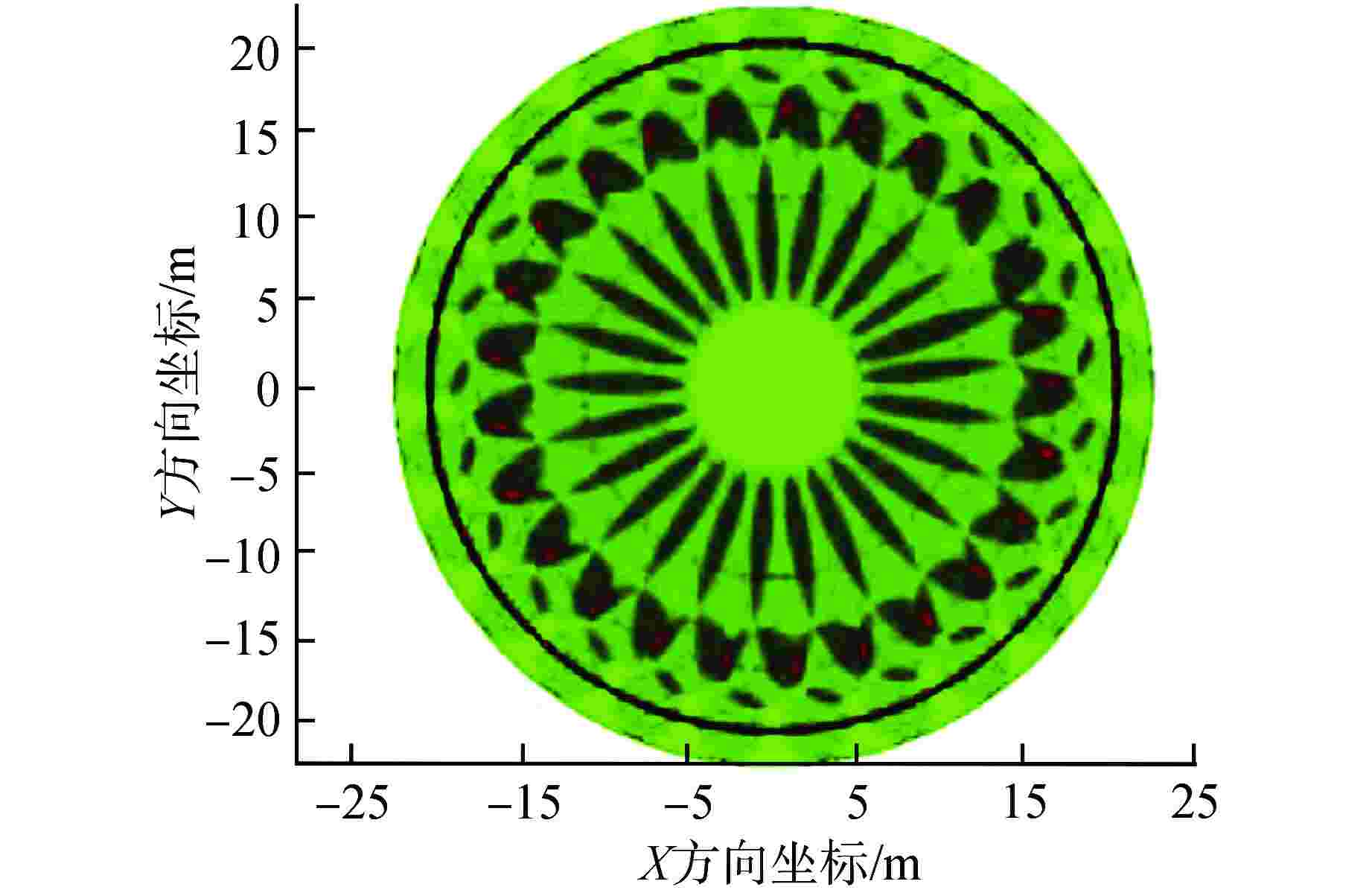
摘要: 为建立安全壳喷淋覆盖率可靠、快速的计算方法，以对安全壳喷淋系统的设计研究提供新的辅助手段，本研究采用理论分析的方法，建立了基于蒙特卡罗模拟法的安全壳喷淋覆盖率计算模型。通过与基于计算机辅助设计（CAD）的安全壳喷淋覆盖率计算结果进行对比，验证基于蒙特卡罗喷淋覆盖率计算方法的适用性。结果表明，两种方法的计算误差在1%以内。因此，本研究建立的基于蒙特卡罗模拟法的安全壳喷淋覆盖率计算方法可靠且具有广泛适用性，对比CAD软件的喷淋覆盖率计算法，新的方法计算速度更快，人因错误率更低，有利于敏感性分析，可大幅提高安全壳喷淋系统设计能力。Abstract: In order to establish a reliable and fast calculation method of containment spray coverage rate, and provide a new auxiliary means for the design and research of the containment spray system, the calculation model of containment spray coverage rate based on Monte Carlo simulation is established in this study by using the method of theoretical analysis. Compared with the calculation results of containment spray coverage rate based on computer aided design (CAD), the applicability of Monte Carlo spray coverage rate calculation method is verified. The results show that the calculation errors of the two methods are within 1%.Therefore, the calculation method of containment spray coverage rate based on Monte Carlo simulation method is reliable and widely applicable. Compared with the spray coverage rate calculation method based on computer aided design (CAD) software, the new method has faster calculation speed and lower human error rate, which is conducive to sensitivity analysis and can greatly improve the design capacity of the containment spray system.
-
Key words:
- Monte Carlo simulation /
- Containment /
- Spray coverage rate
-
图 3 喷淋覆盖率计算结果与模拟次数关系
Figure 3. Relationship between Spray Coverage Rate Calculation Results and Simulation Times
图 5 基于蒙特卡罗模拟的喷淋覆盖覆盖面（优化后）
Figure 5. Spray Coverage Based on Monte Carlo Simulation (Optimized)
表 1 安全壳喷淋系统优化参数
Table 1. Optimization Parameters of Containment Spray System
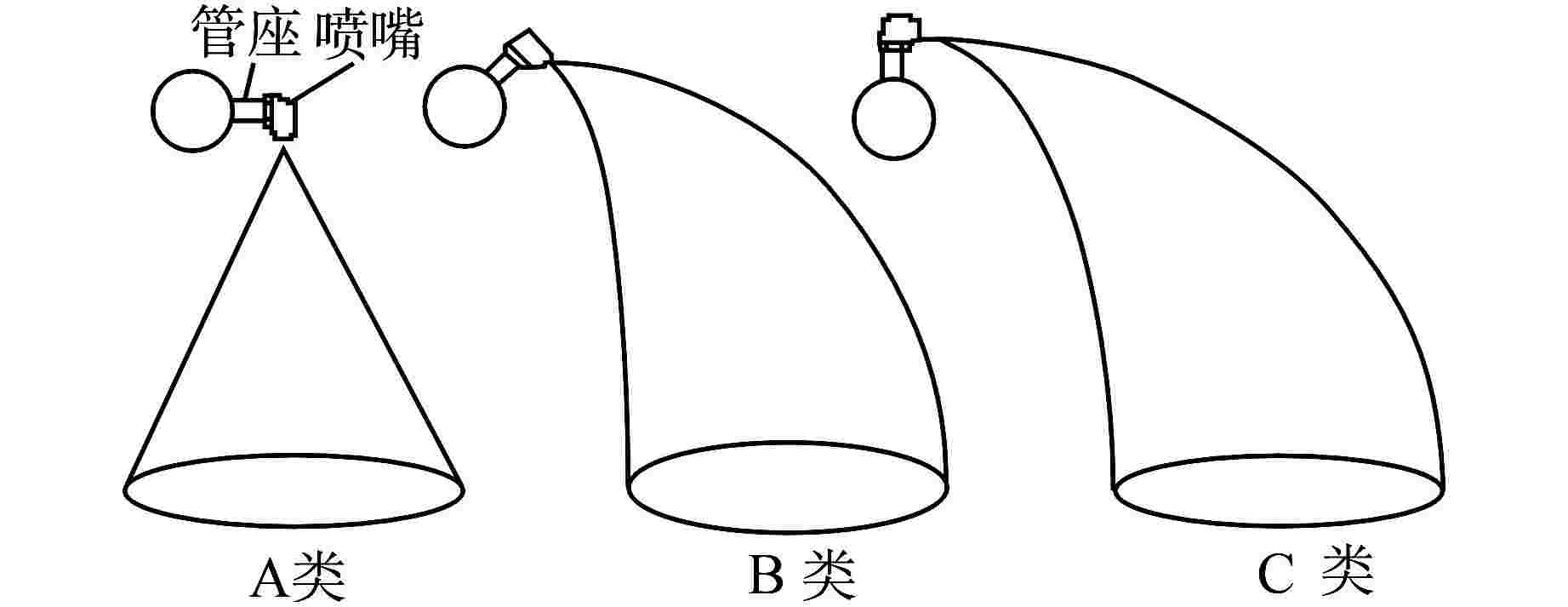
喷头 数量 长半径/m 短半径/m 偏移/m 截面半径/m 环吊半径/m A 25 2.2 2.2 0 22.5 20 B 25 2.45 2.43 1.17 C 25 6.6 1.9 2.58 
下载: 导出CSV
-
[1] 吴义纯,丁明. 基于蒙特卡罗仿真的风力发电系统可靠性评价[J]. 电力自动化设备,2004, 24(12): 70-73. doi: 10.3969/j.issn.1006-6047.2004.12.021 [2] 孙海虹,叶晓甦. 基于蒙特卡罗模拟技术的工程造价风险因素分析[J]. 重庆建筑大学学报,2005, 27(6): 121-126. [3] 玉宇,童节娟,赵军,等. 应用蒙特卡罗方法模拟核电厂丧失设备冷却水系统始发事件的频率[J]. 核动力工程,2010, 31(4): 57-60. [4] 广东核电培训中心. 900MW压水堆核电站系统与设备(上册)[M]. 北京: 原子能出版社, 2005: 91-95. [5] 尹增谦,管景峰,张晓宏,等. 蒙特卡罗方法及应用[J]. 物理与工程,2002, 12(3): 45-49. doi: 10.3969/j.issn.1009-7104.2002.03.014 [6] 王中伟. 用EXCEL实现工程项目的蒙特卡洛模拟分析[J]. 广东交通职业技术学院学报,2005, 4(1): 101-103. doi: 10.3969/j.issn.1671-8496.2005.01.031 [7] 张建中. 蒙特卡洛方法(I)[J]. 数学的实践与认识,1974, 1(1): 28-40. [8] DURRETT R. Probability: theory and examples[M]. 4th ed. Cambridge: Cambridge University Press, 2010: 76-81. -
图(5) / 表(1)
计量
- 文章访问数: 195
- HTML全文浏览量: 44
- PDF下载量: 29
- 被引次数: 0
