PSA-Based Uncertainty Analysis of Pressurized Water Reactor LBLOCA
-
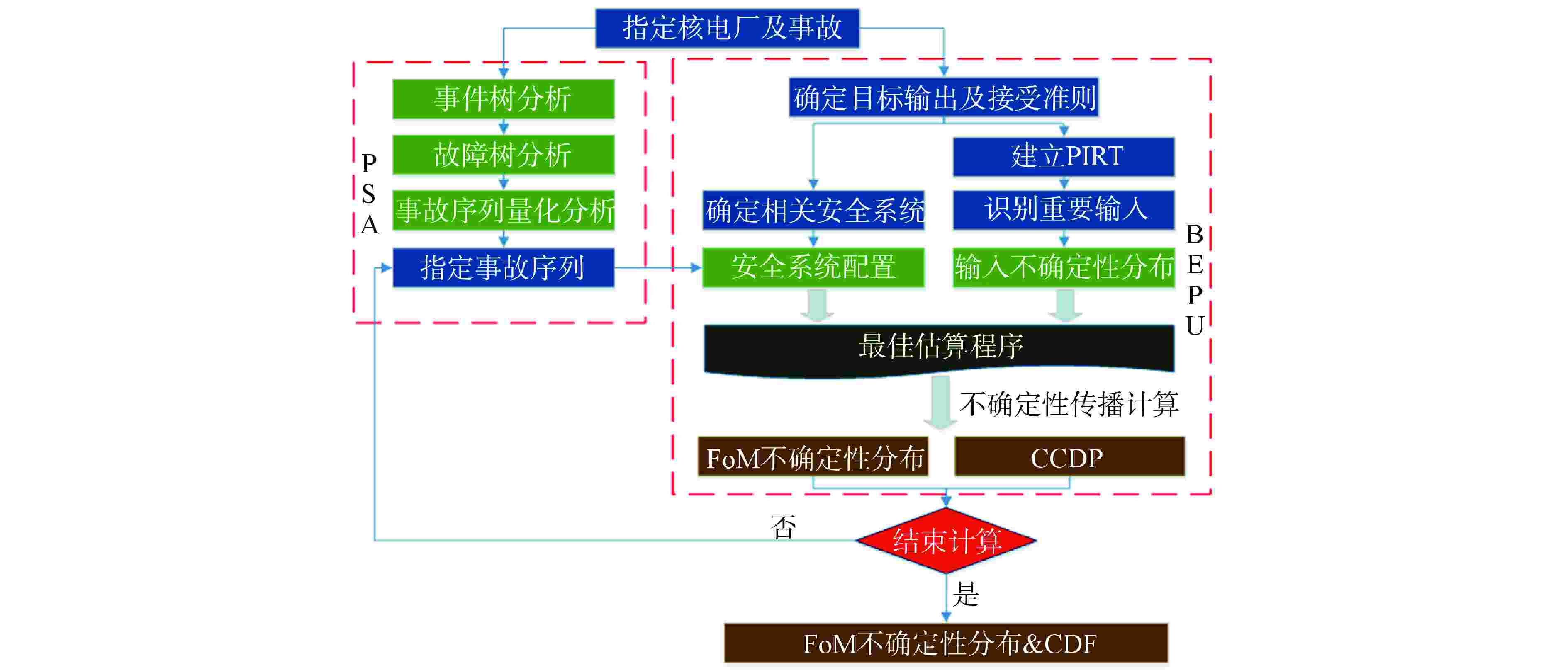
摘要: 为了结合确定论与概率论分析开展更加真实的核反应堆事故工况安全分析，提出了一种结合概率安全分析（PSA）和最佳估算加不确定性（BEPU）分析的方法，并以典型三环路压水堆冷管段双端断裂大破口失水事故（LBLOCA）的极限事故为对象，首先基于PSA开展了应急堆芯冷却系统的事故失效分析，而后结合BEPU分析评估了事件树中各事故序列的包壳峰值温度（PCT）分布及条件堆芯损坏概率（CCDP），最终确定了压水堆在该事故工况中的堆芯损坏频率（CDF）。分析结果表明，压水堆在冷管段双端断裂工况中应急堆芯冷却系统能够保证反应堆的安全，且一列低压安注系统足以排出堆芯余热及保证反应堆安全。
-
关键词:
- 大破口失水事故（LBLOCA） /
- 不确定性分析 /
- 概率安全分析（PSA） /
- 风险指引
Abstract: In order to combine deterministic and probabilistic analysis to carry out more realistic safety analysis of nuclear reactor accident conditions, a method combining probabilistic safety analysis (PSA) and best estimate plus uncertainty (BEPU) analysis is proposed, the extreme accident of the double-ended fracture large-break loss of water accident (LBLOCA) in a typical three-loop pressurized water reactor cold pipe section is taken as the object. First, the accident failure analysis of the emergency core cooling system is carried out based on PSA. Then, combined with BEPU analysis, the cladding peak temperature (PCT) distribution and conditional core damage probability (CCDP) of each accident sequence in the event tree are evaluated, and the core damage frequency of the PWR in this accident condition is finally determined. The analysis results show that the emergency core cooling system of PWR can ensure the safety of the reactor under the condition of double-ended fracture of cold pipe section, and a row of low-pressure safety injection systems are sufficient to remove the residual heat of the core and ensure the safety of the reactor. -
图 1 BEPU与PSA结合框架示意图
PIRT—现象识别排序表
Figure 1. Schematic Diagram of Frame Combining BEPU and PSA
图 2 ECCS事件树分析
F—失效；S—有效；CD—堆芯损坏；HPIS—高压安注系统； LPIS—低压安注系统；ACC—安注箱
Figure 2. Event Tree Analysis of ECCS
表 1 LBLOCA工况输入参数
Table 1. Input Parameters of LBLOCA Condition
参数 区间 分布 衰变功率修正系数 (0.92, 1.08) 正态 气隙等效尺寸修正系数 (0.8, 1.2) 正态 UO2体积热容修正系数 (0.98, 1.02) 正态 UO2热导率修正系数 (0.9, 1.1) 正态 初始功率/MW (2837.1, 2952.9) 正态 热棒径向峰值因子修正系数 (0.95, 1.05) 正态 热棒轴向峰值因子修正系数 (0.95, 1.05) 正态 上封头初始温度/K (565.94, 575.94) 均匀 完整回路冷段温度/K (563.94, 567.94) 正态 完整回路热段温度/K (598.36, 602.36) 正态 破口回路冷段温度/K (563.94, 567.94) 正态 破口回路热段温度/K (598.36, 602.36) 正态 破口背压修正系数 (0.85, 1.15) 均匀 稳压器初始液位/m (6.9, 7.1) 正态 稳压器初始压力/MPa (15.4, 15.6) 正态 稳压器波动管形阻修正系数 (0.5, 2.0) 对数正态 主泵扬程两相修正因子 (0.9, 1.1) 正态 主泵转矩两相修正因子 (0.9, 1.1) 正态 主泵形阻压降修正系数 (0.5, 2.0) 对数正态 安注箱初始压力/MPa (4.33, 4.73) 正态 安注箱管线形阻系数修正系数 (0.5, 2.0) 对数正态 安注箱初始水温/K (313.15, 333.15) 正态 包壳氧化Cathcart-Pawel模型精度 (0.61, 1.16) 正态 临界热流密度查询表模型精度 (0.77, 1.63) 正态 膜态沸腾液相换热模型精度 (0.59, 2.06) 对数正态 膜态沸腾气相换热模型精度 (0.44, 1.92) 对数正态 再淹没膜态沸腾液相换热模型精度 (1.02, 1.90) 对数正态 再淹没膜态沸腾气相换热模型精度 (1.32, 2.58) 对数正态 两相界面阻力模型精度 (0.48, 2.82) 对数正态 液滴夹带份额修正系数 (0.71, 1.60) 正态 相界面冷凝换热模型精度 (0.53, 1.92) 正态 临界流Henry-Fauske模型精度 (0.76, 1.26) 正态 CCFL模型气相截距修正系数 (0.9, 1.1) 均匀 上腔室形阻系数修正系数 (0.5, 2.0) 对数正态 堆芯形阻系数修正系数 (0.8, 1.2) 均匀 旁流通道壁面粗糙度修正系数 (0.5, 2.0) 对数正态 堆芯水力学直径修正系数 (0.98, 1.02) 正态 燃料棒气隙初始压力/MPa (6.2, 6.4) 正态 下降段水力学直径修正系数 (0.98, 1.02) 正态 下降段管道壁面粗糙度修正系数 (0.5, 2.0) 对数正态 完整回路冷管壁粗糙度修正系数 (0.5, 2.0) 对数正态 热段水力学直径修正系数 (0.98, 1.02) 正态 破口回路冷管壁粗糙度修正系数 (0.5, 2.0) 对数正态 蒸汽发生器管道堵塞率 (0, 5%) 正态 蒸汽发生器形阻系数修正系数 (0.8, 1.2) 均匀 安注信号触发压力/MPa (11.76, 11.92) 正态 低压安注水温/K (313.15, 333.15) 正态 
下载: 导出CSV
表 2 LBLOCA工况PSA+BEPU分析结果综合
Table 2. Results of PSA+BEPU Analysis for LBLOCA Condition
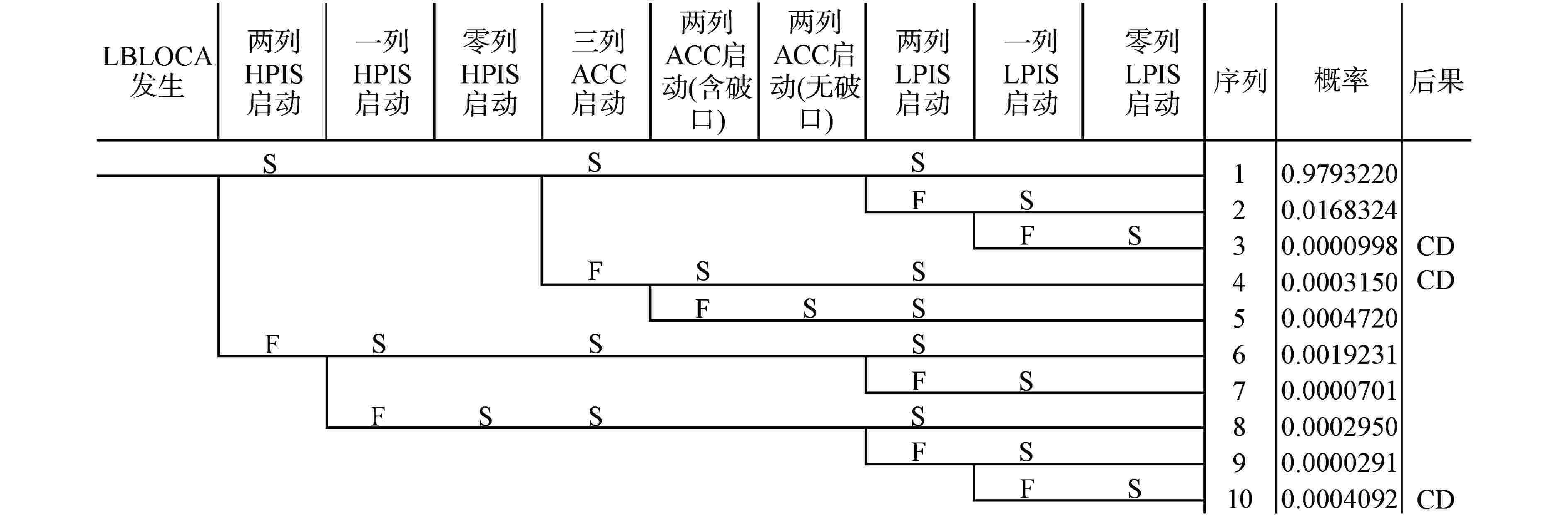
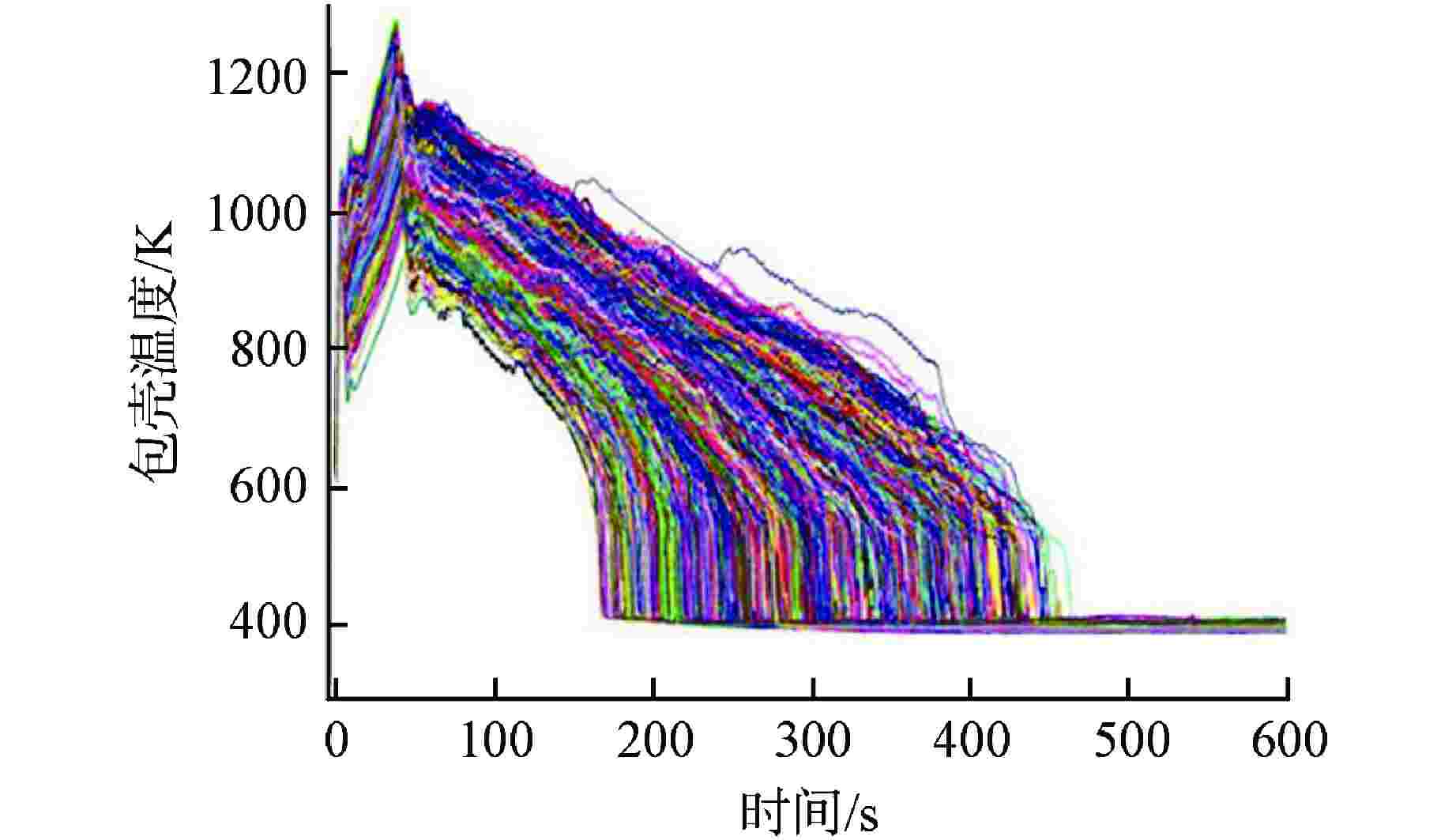
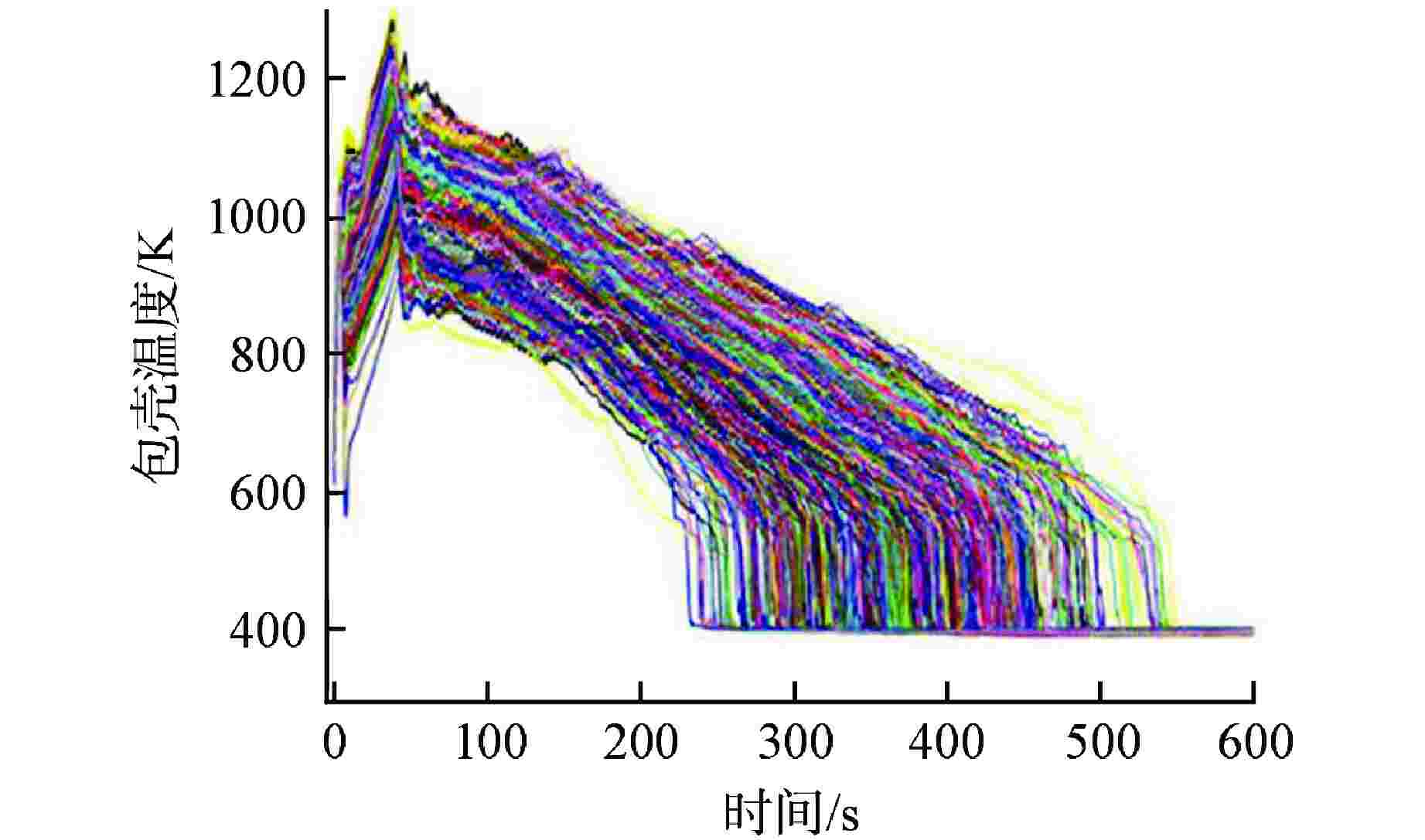
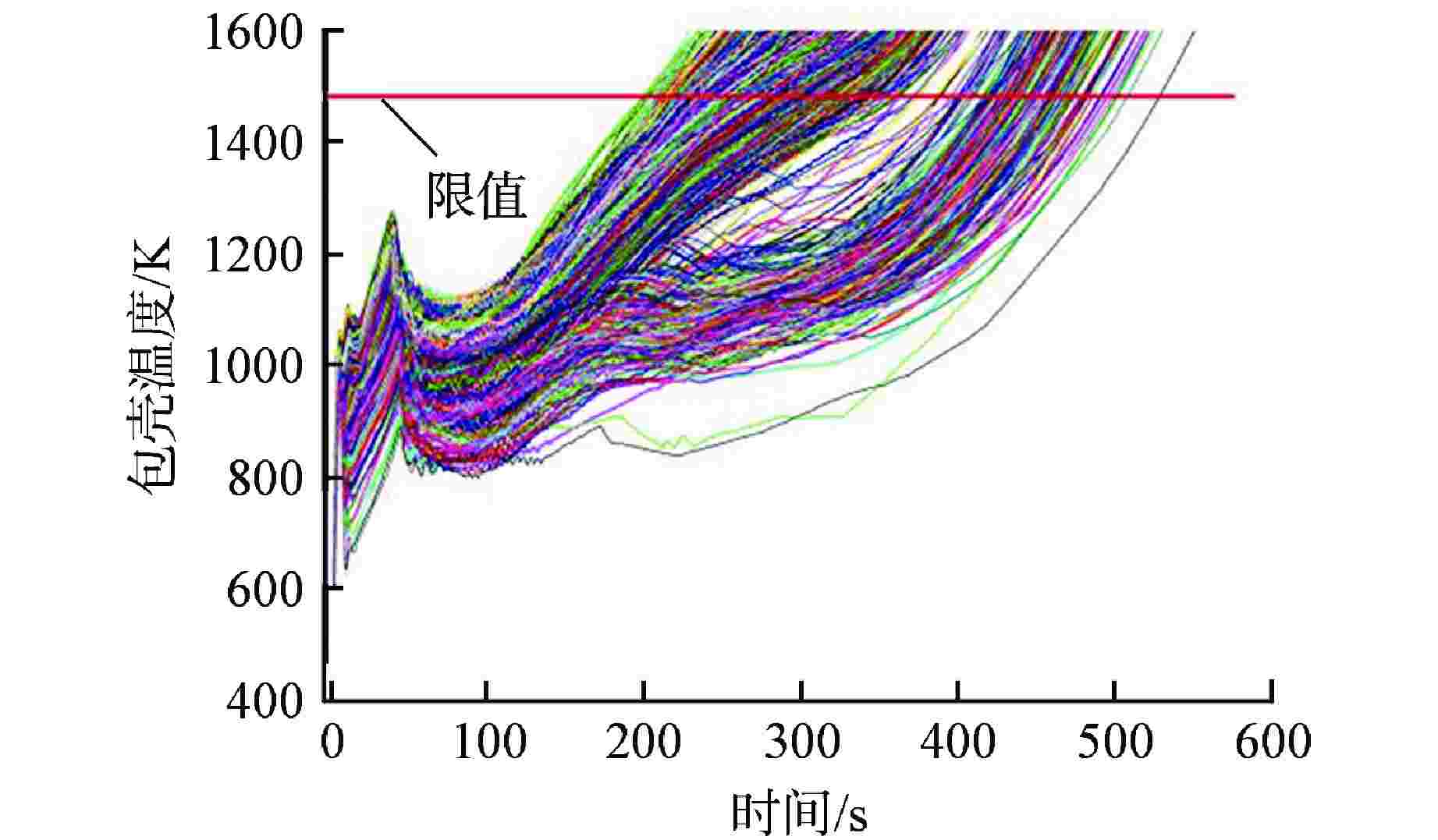
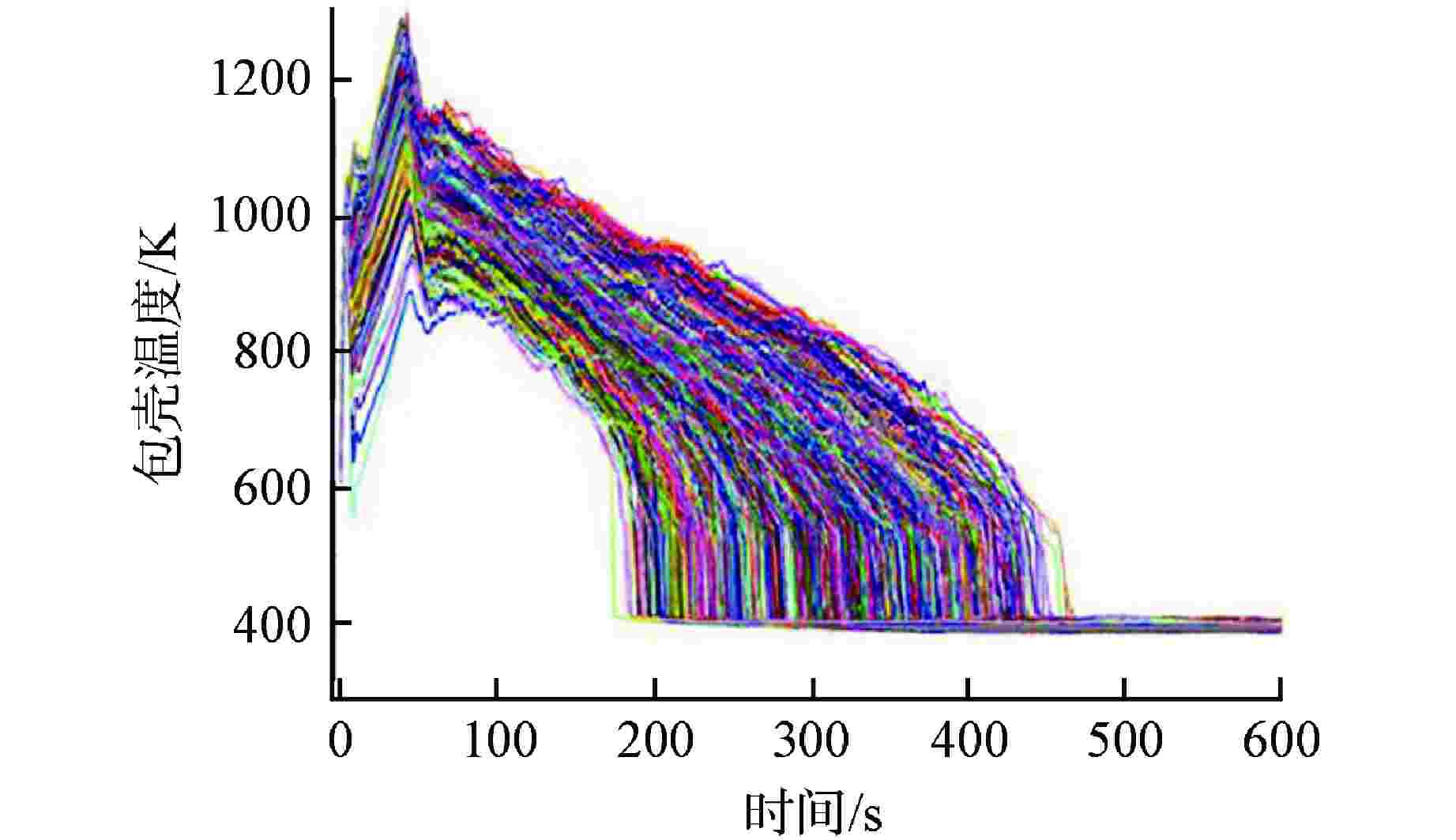
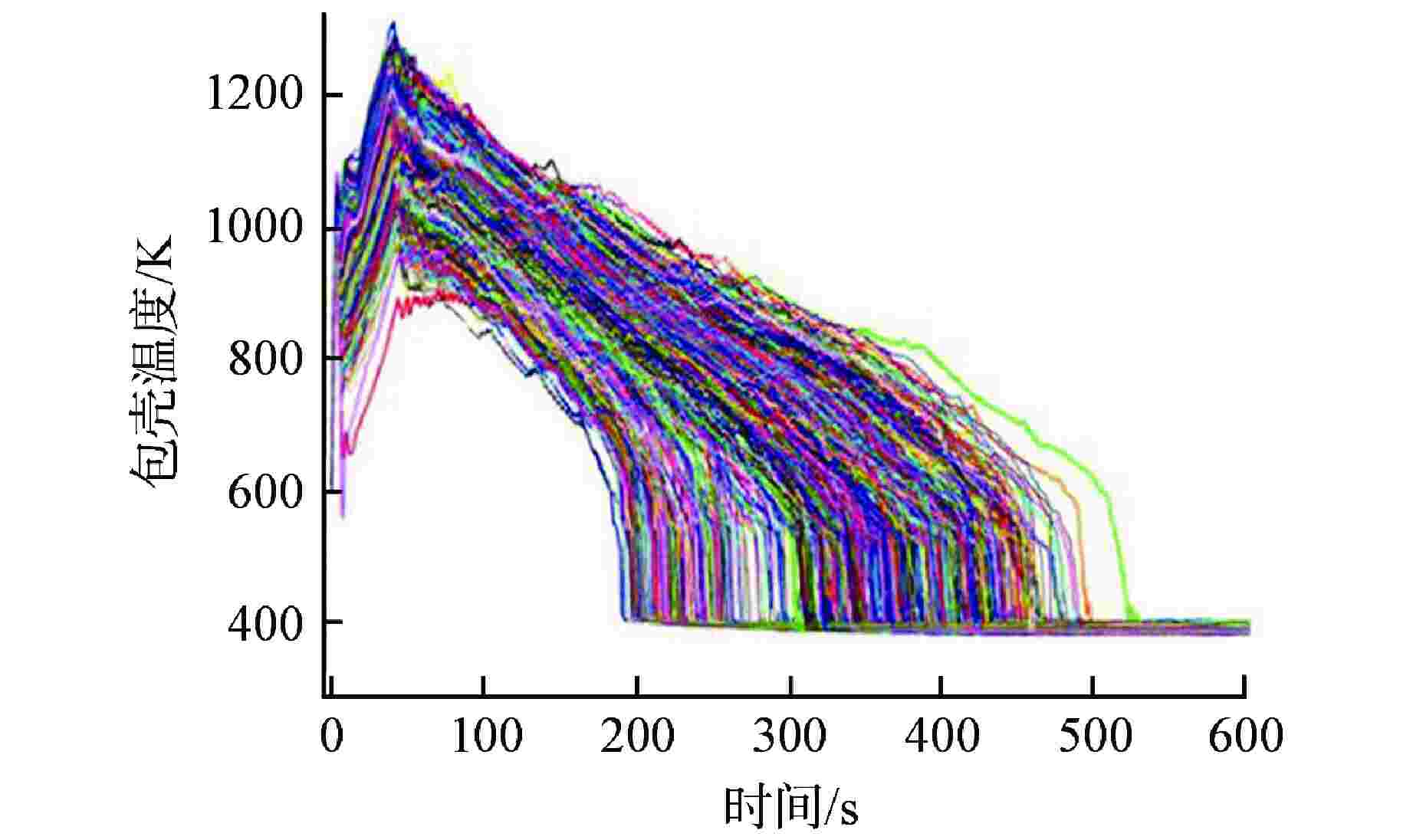
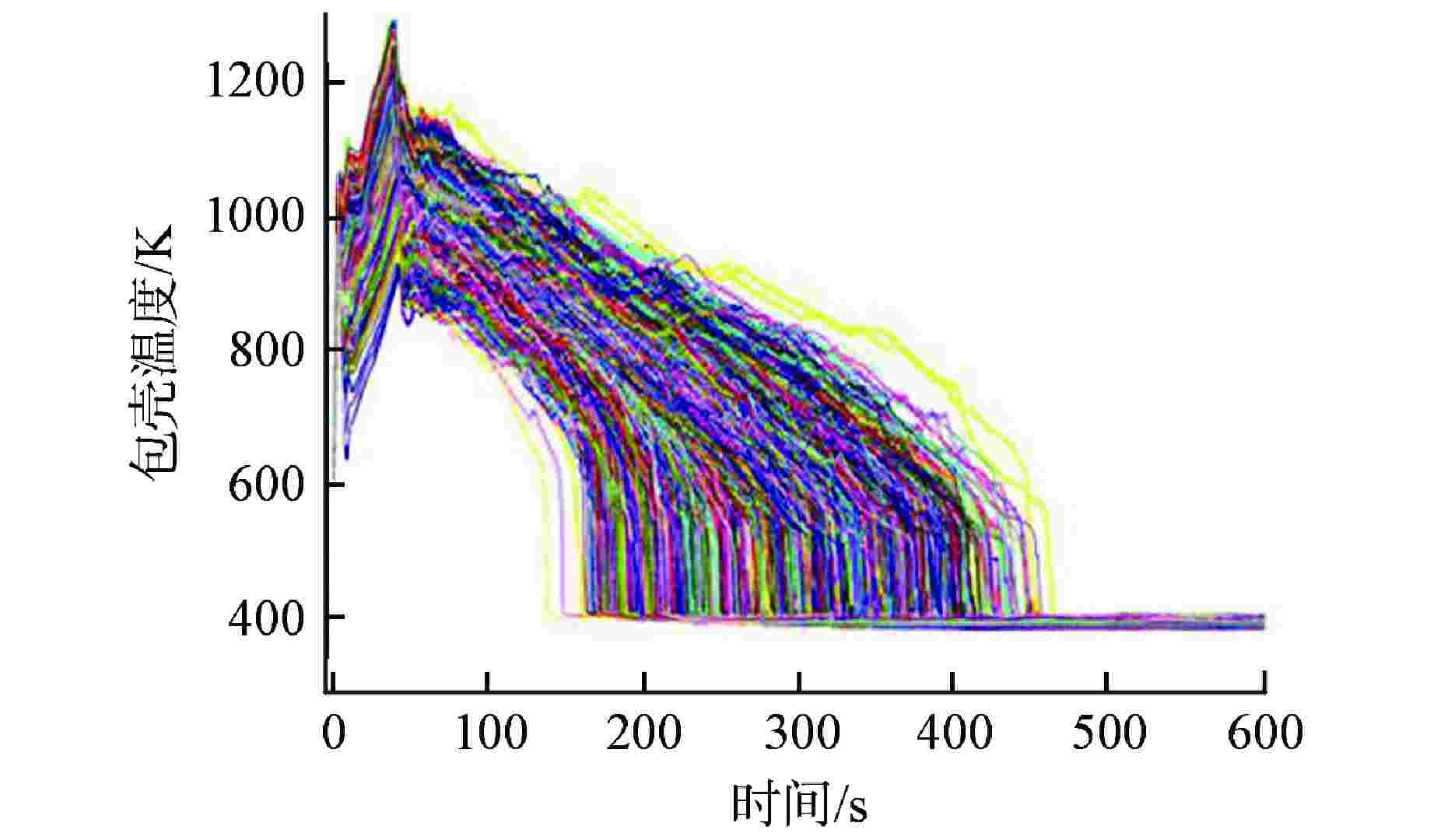
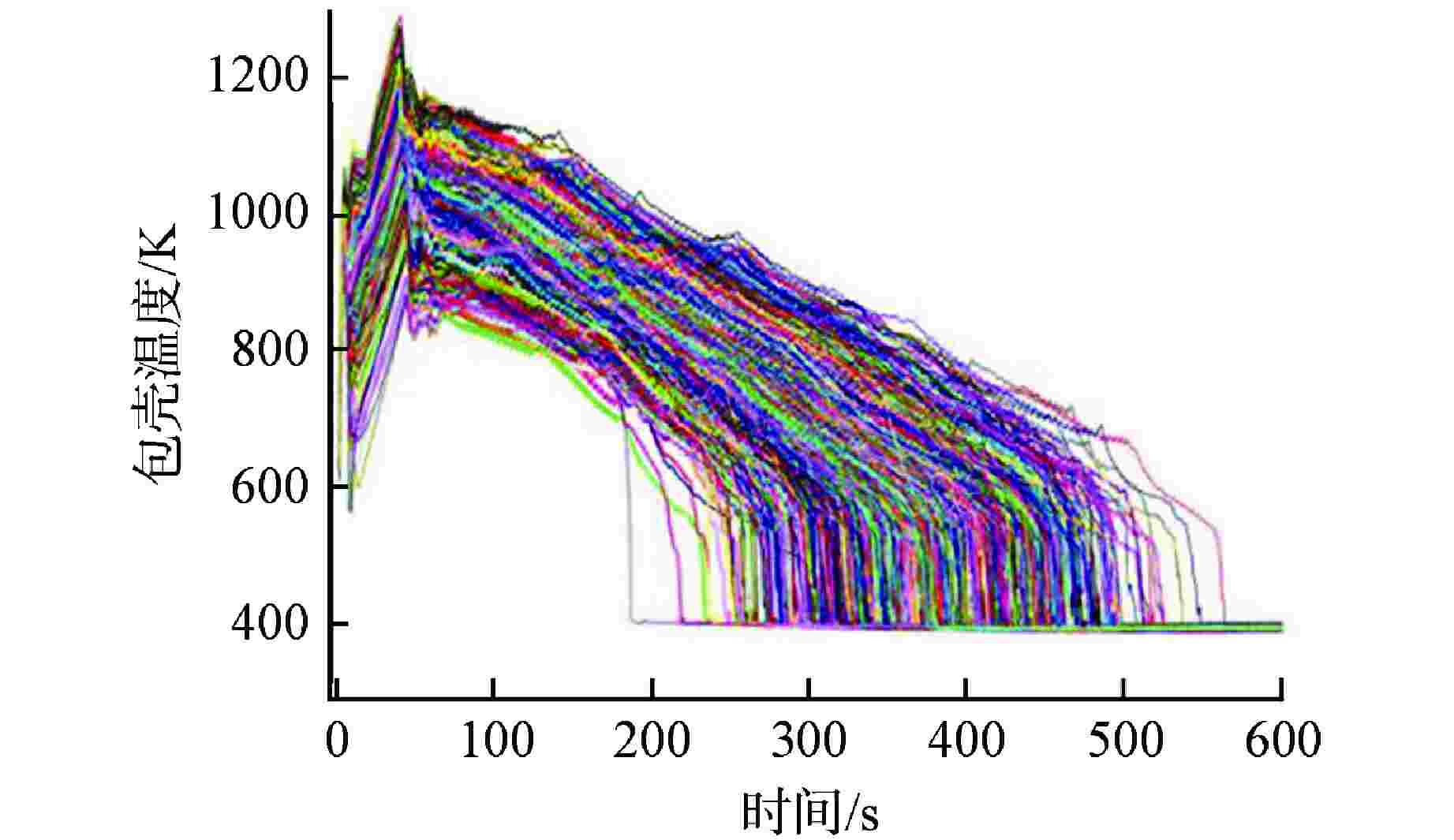
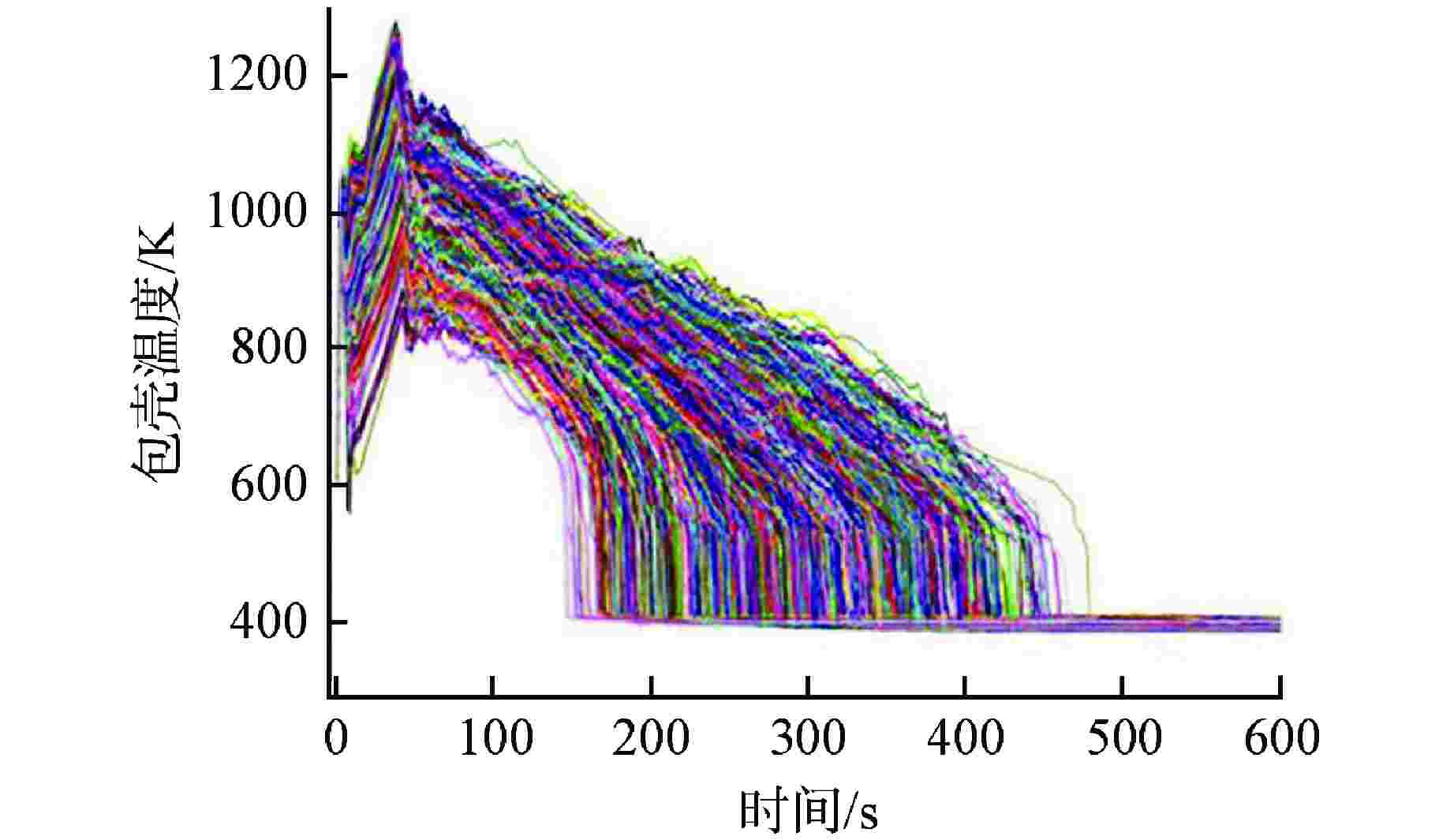
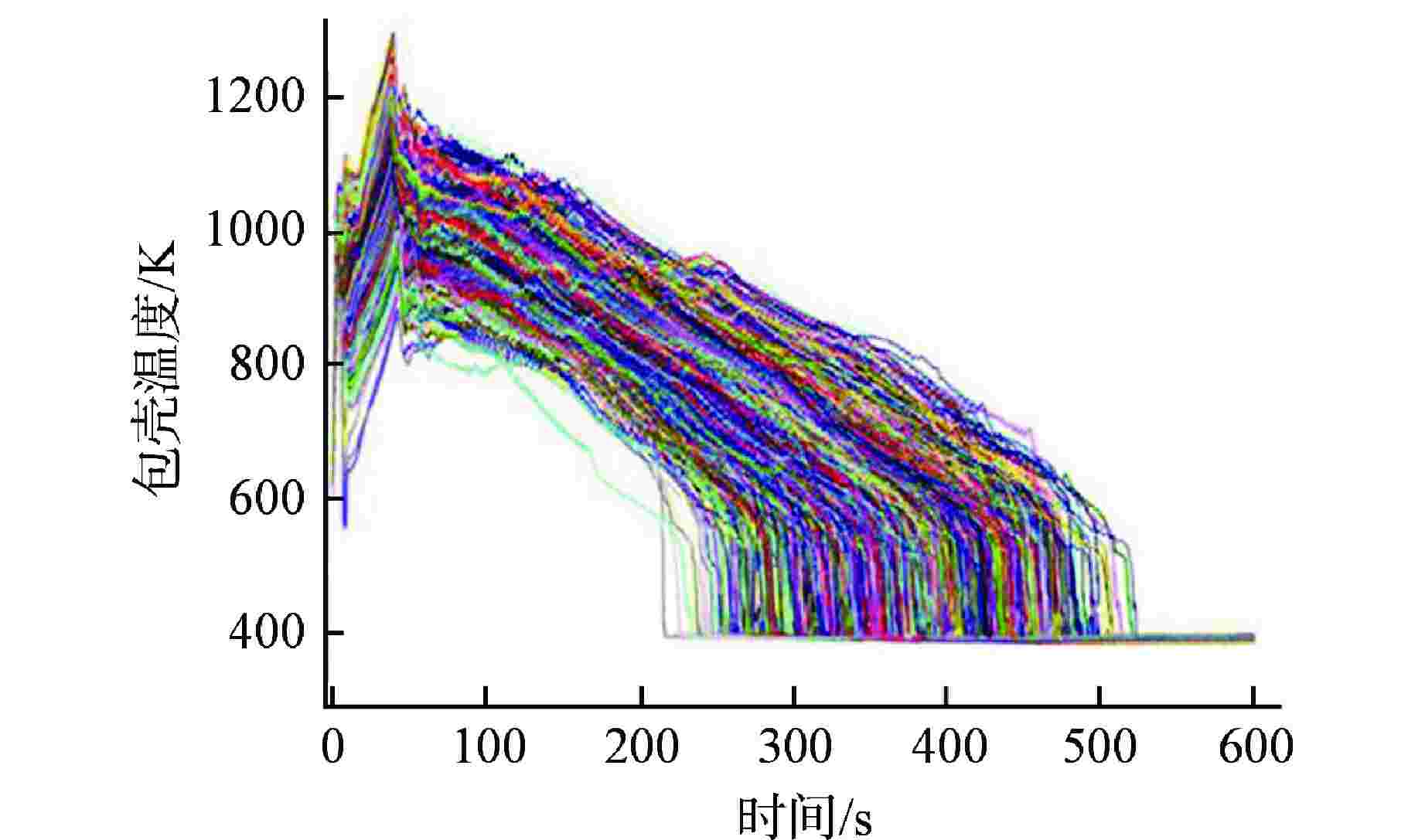
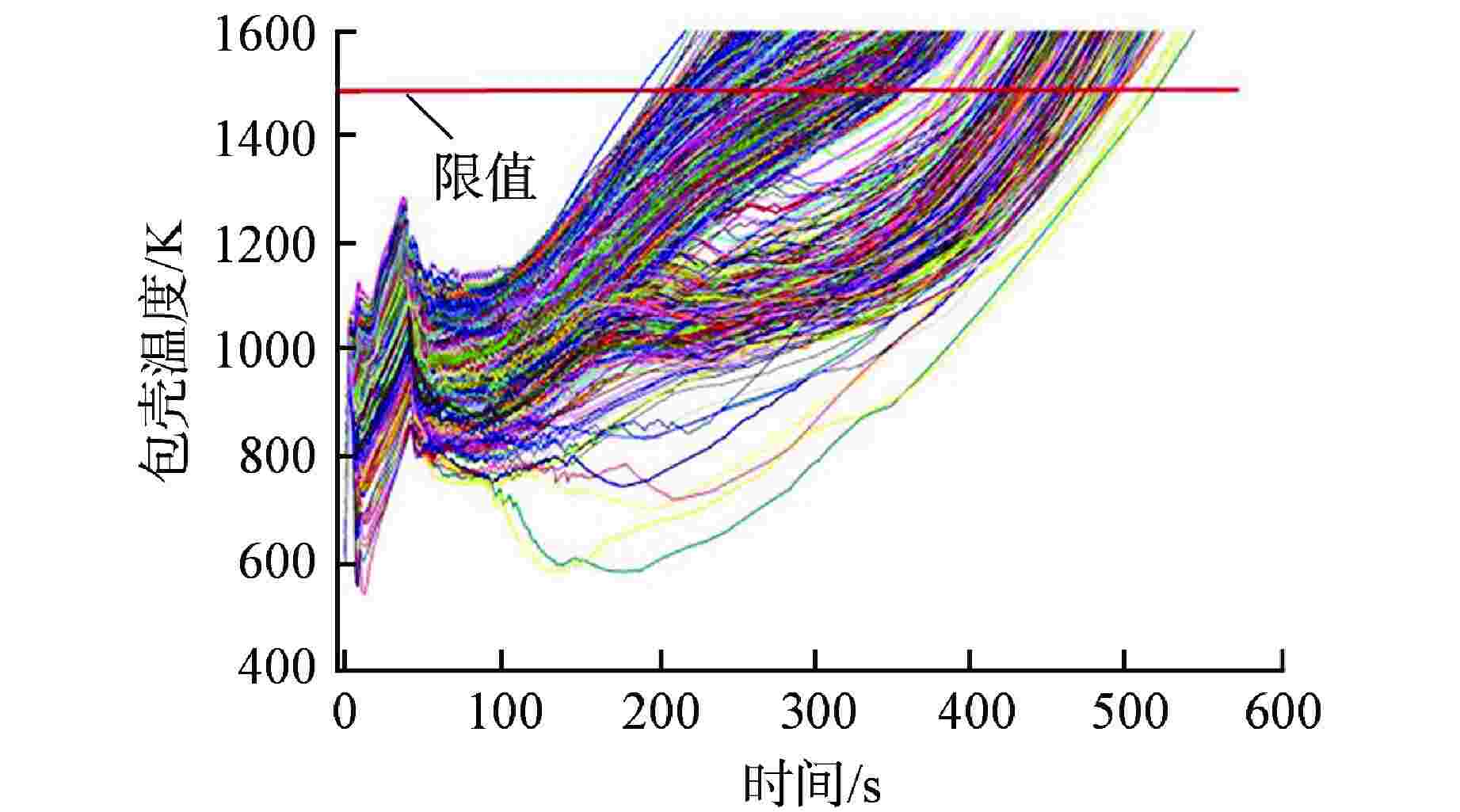
序列 安注系统可用性 概率 BEPU计算PCT95%置信上限/K BEPU计算PCT最大值/K 1 2高压+3中压（1列破口）+2低压 0.9793220 1245.23 1279.52 2 2高压+3中压（1列破口）+1低压 0.0168324 1249.36 1295.32 3 2高压+3中压（1列破口）+0低压 0.0000998 F F 4 2高压+2中压（1列破口）+2低压 0.0003150 1262.14 1301.25 5 2高压+2中压（0列破口）+2低压 0.0004720 1259.13 1310.32 6 1高压+3中压（1列破口）+2低压 0.0019231 1244.15 1296.64 7 1高压+3中压（1列破口）+1低压 0.0000701 1251.26 1291.20 8 0高压+3中压（1列破口）+2低压 0.0002950 1246.43 1293.19 9 0高压+3中压（1列破口）+1低压 0.0000291 1253.11 1305.19 10 0高压+3中压（1列破口）+0低压 0.0004092 F F
下载: 导出CSV
-
[1] 单建强, 廖承奎, 苟军利, 等. 压水堆核电厂瞬态安全数值分析方法[M]. 西安: 西安交通大学出版社, 2016: 229. [2] 周法清. 核电厂概率安全评价[M]. 上海: 上海交通大学出版社, 1996: 243. [3] IAEA. Safety margins of operating reactors analysis of uncertainties and implications for decision making: IAEA TECDOC No. 1332[R]. Vienna: IAEA, 2003. [4] 靖剑平,贾斌,高新力,等. 最佳估算加不确定性分析方法在我国核安全审评中的应用[J]. 核安全,2016, 15(4): 11-17. [5] IAEA. Accident analysis for nuclear power plants: safety reports series No. 23[R]. Vienna: IAEA, 2002. [6] KANG D G, AHN S H, CHANG S H. A combined deterministic and probabilistic procedure for safety assessment of beyond design basis accidents in nuclear power plant: application to ECCS performance assessment for design basis LOCA redefinition[J]. Nuclear Engineering and Design, 2013, 260: 165-174. doi: 10.1016/j.nucengdes.2013.03.033 [7] MARTORELL S, SÁNCHEZ-SÁEZ F, VILLANUEVA J F, et al. An extended BEPU approach integrating probabilistic assumptions on the availability of safety systems in deterministic safety analyses[J]. Reliability Engineering & System Safety, 2017, 167: 474-483. [8] DU Y, LI H X, LIANG T H, et al. Uncertainty analysis of the conditional exceedance probability calculation for a probabilistically significant SBO sequence[J]. Nuclear Technology, 2019, 205(1-2): 128-139. doi: 10.1080/00295450.2018.1494998 [9] DENG J, DING S H, LI Z C, et al. The development of ARSAC for modeling nuclear power plant system[J]. Progress in Nuclear Energy, 2021, 140: 103880. doi: 10.1016/j.pnucene.2021.103880 [10] NISSLEY M E, FREPOLI C, OHKAWA K, et al. Realistic large-break LOCA evaluation methodology using the automated statistical treatment of uncertainty method (ASTRUM): Westinghouse Propriety Report, WCAP-1[R]. 2003 [11] IAEA. Procedures for conducting probabilistic safety assessments of nuclear power plants (level 1): IAEA safety series NO. 50-p-4[R]. Vienna: IAEA, 1992. [12] ZIO E. Integrated deterministic and probabilistic safety assessment: concepts, challenges, research directions[J]. Nuclear Engineering and Design, 2014, 280: 413-419. doi: 10.1016/j.nucengdes.2014.09.004 [13] 王洋洋. 核电厂典型事故分析不确定性评价方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2017. [14] 宋建阳,杨江,刘井泉,等. 风险指引的CPR1000核电厂LBLOCA分析方法初步研究[J]. 原子能科学技术,2018, 52(6): 1028-1033. doi: 10.7538/yzk.2017.youxian.0497 [15] BOYACK B, DUFFEY R, GRIFFITH G, et al. Quantifying reactor safety margins: application of code scaling, applicability, and uncertainty evaluation methodology to a large-break, loss-of-coolant accident: NUREG/CR-5249[R]. Washington: EG&G Idaho, 1989. [16] XIONG Q W, GOU J L, CHEN W, et al. Investigation of uncertainty quantification methods for constitutive models and the application to LOFT LBLOCA[J]. Annals of Nuclear Energy, 2019, 132: 119-133. doi: 10.1016/j.anucene.2019.04.028 [17] REVENTOS F, PEREZ M, BATET L, et al. BEMUSE phase V report: uncertainty and sensitivity analysis of a LBLOCA in Zion nuclear power plant: NEA/SCNI/R(2009)13[R]. OECD, 2009 [18] USNRC. Estimating loss-of-coolant accident (LOCA) frequencies through the elicitation process: NUREG-1829[R]. Washington: USNRC, 2008. -
图(12) / 表(2)
计量
- 文章访问数: 163
- HTML全文浏览量: 92
- PDF下载量: 50
- 被引次数: 0
