Simulation Study on Fluid-elastic Instability of Two-Dimensional Tube Bundle Based on UDF
-
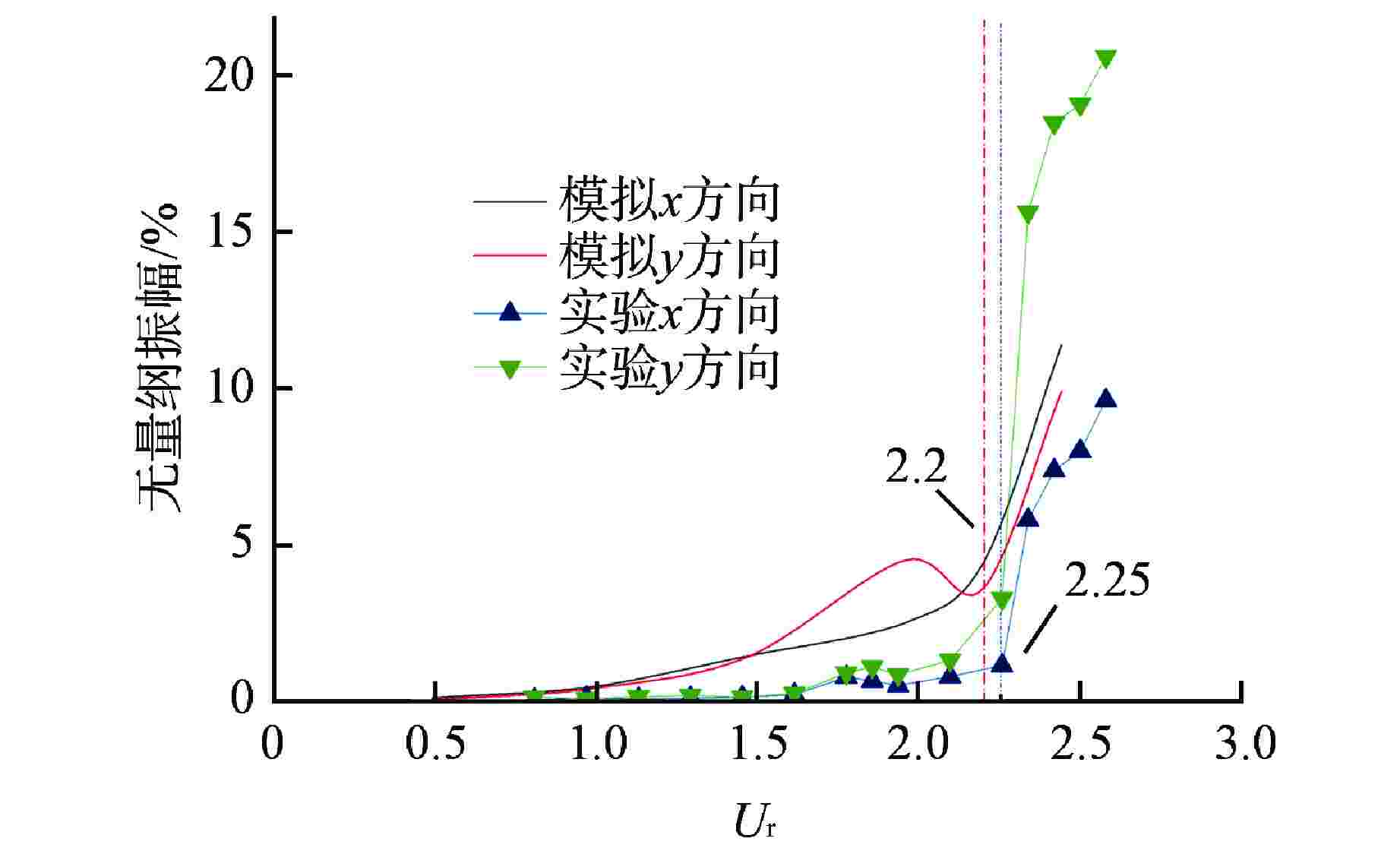
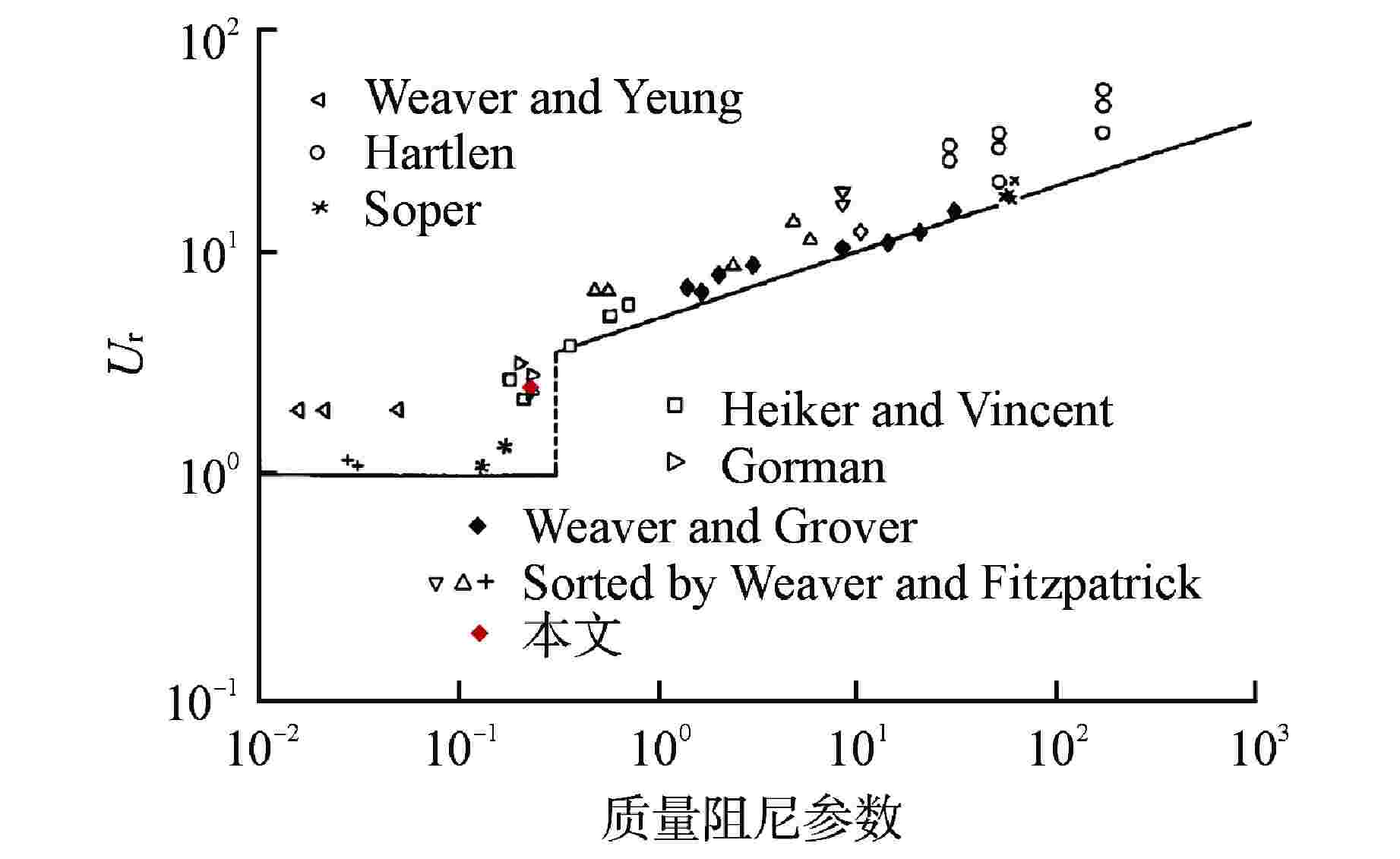
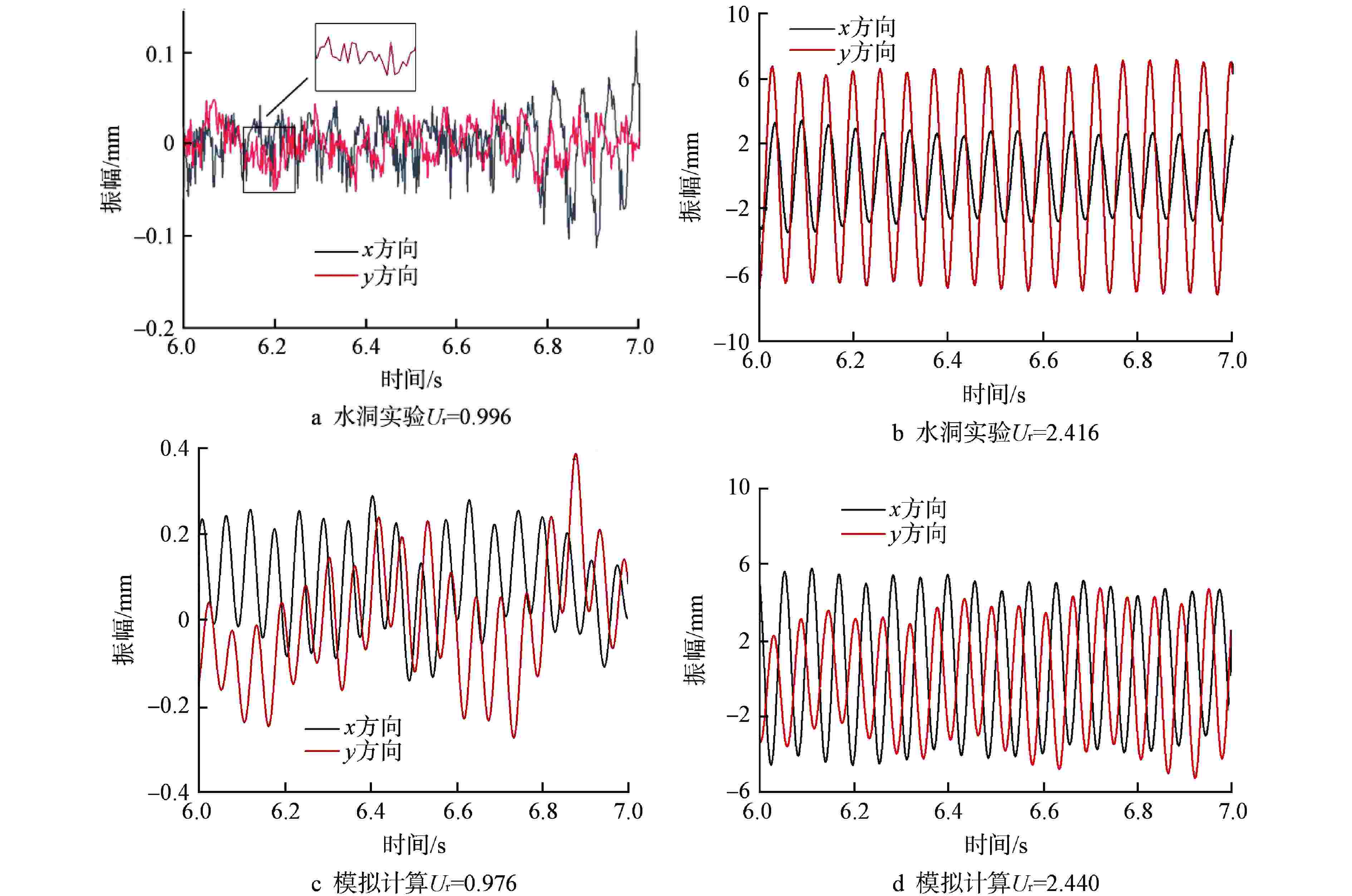
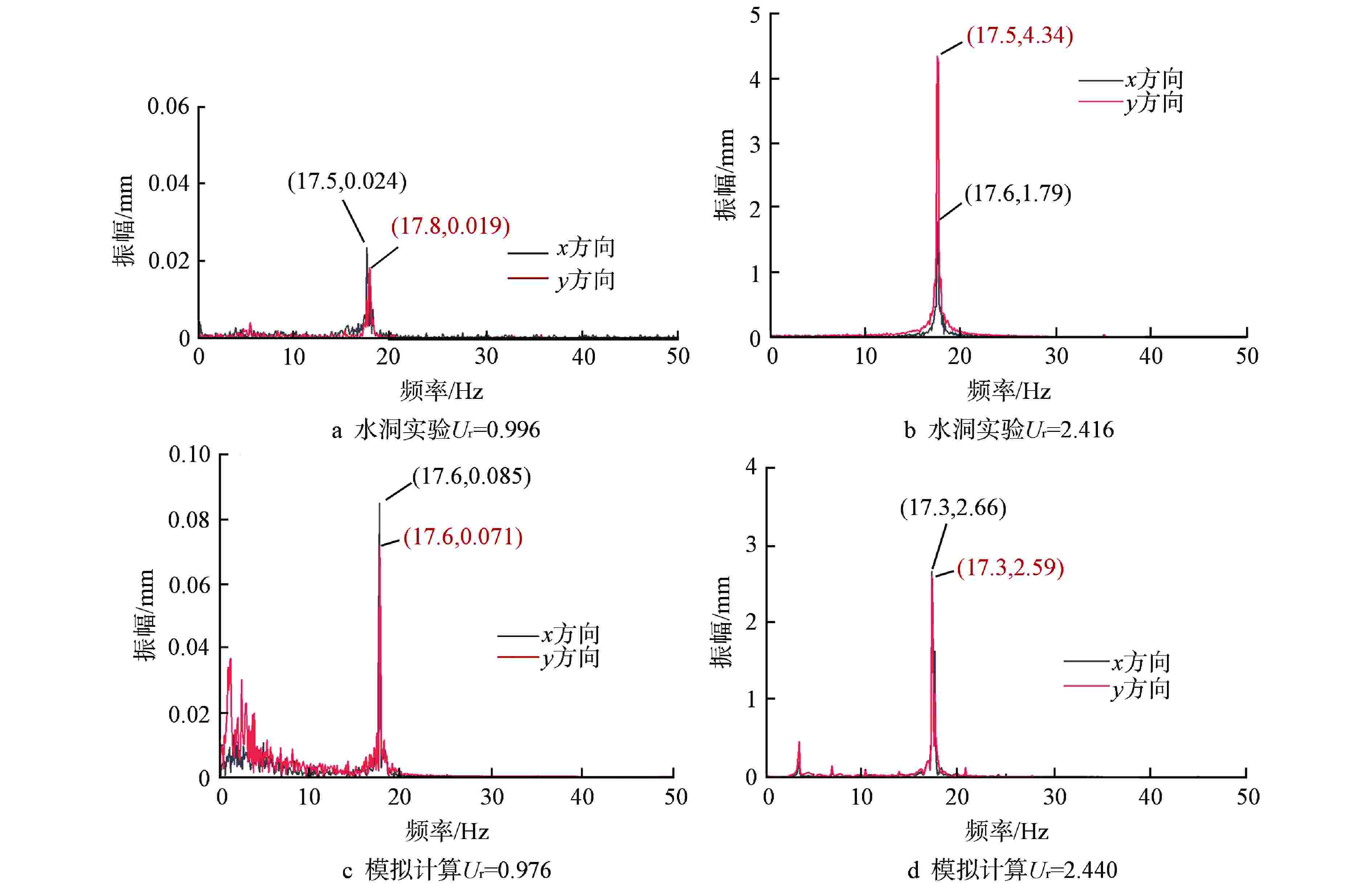
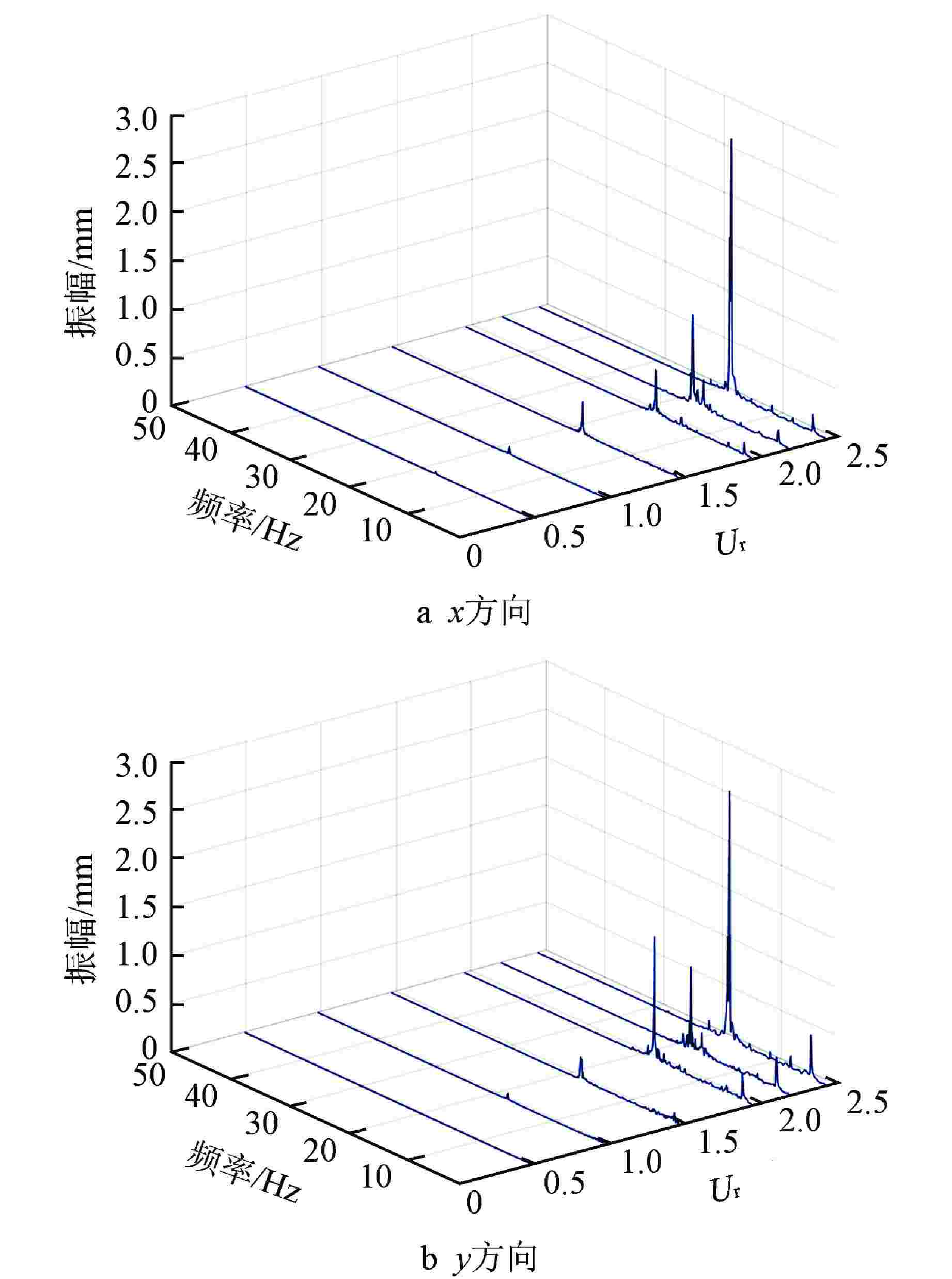
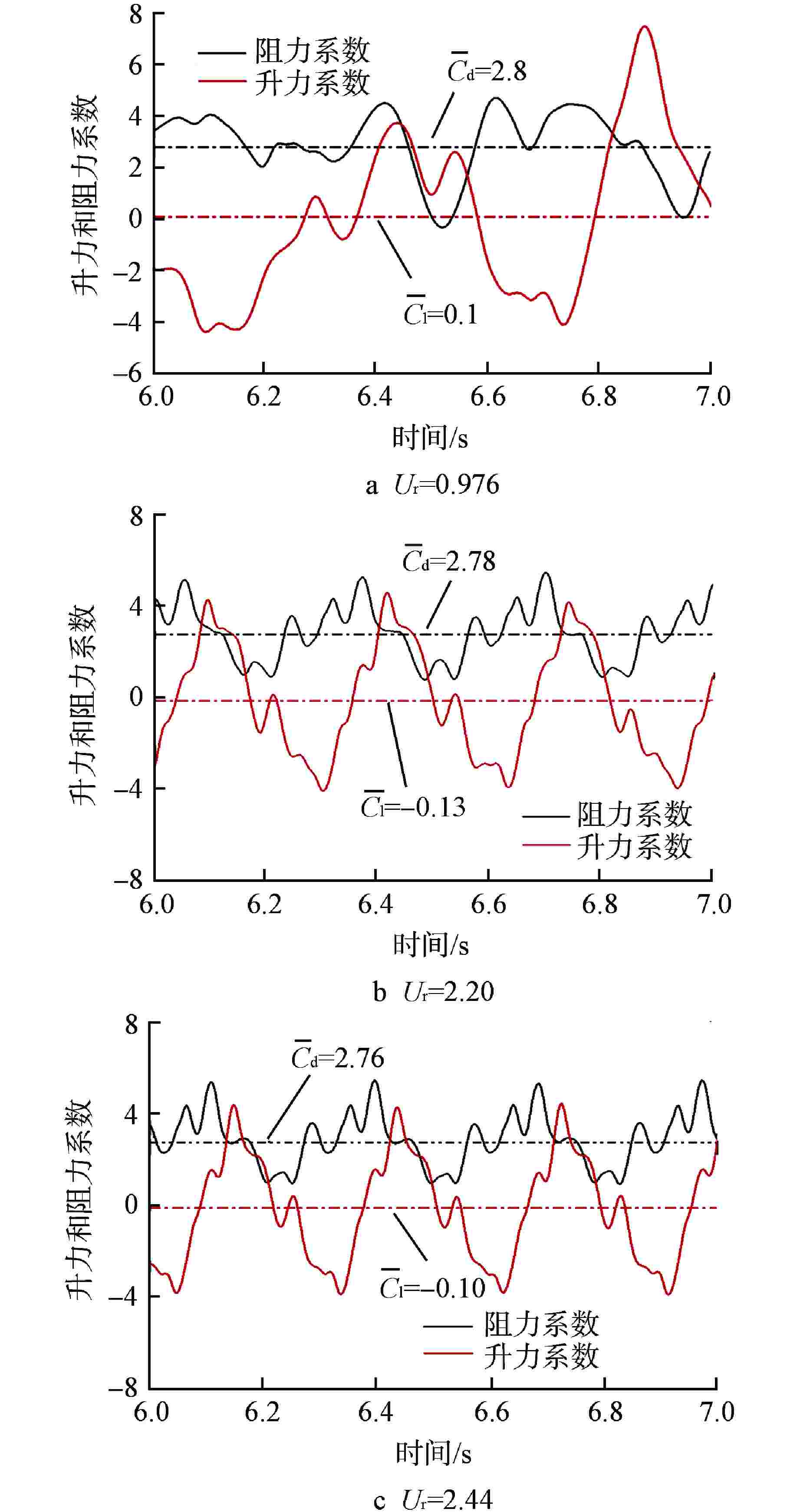
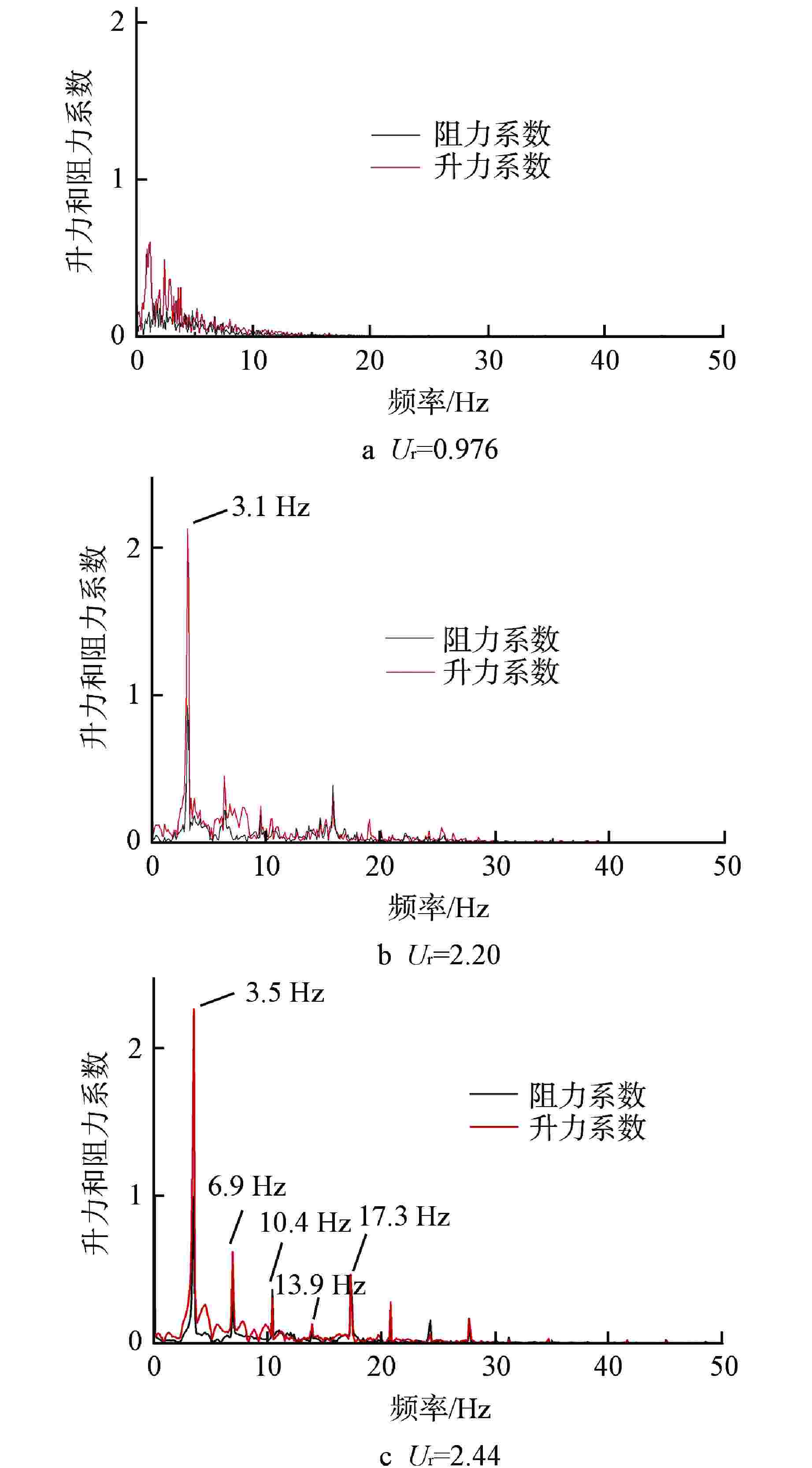
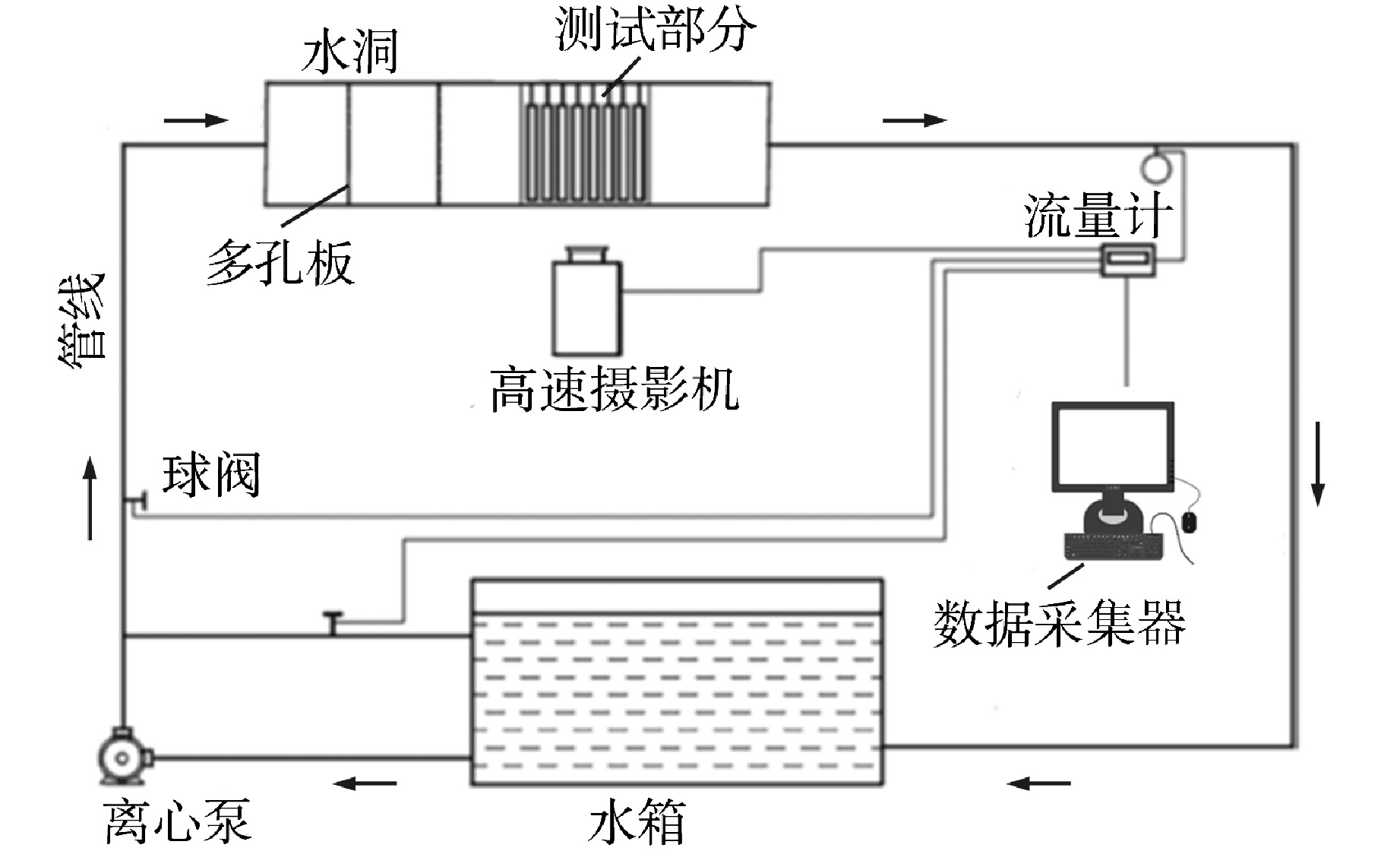
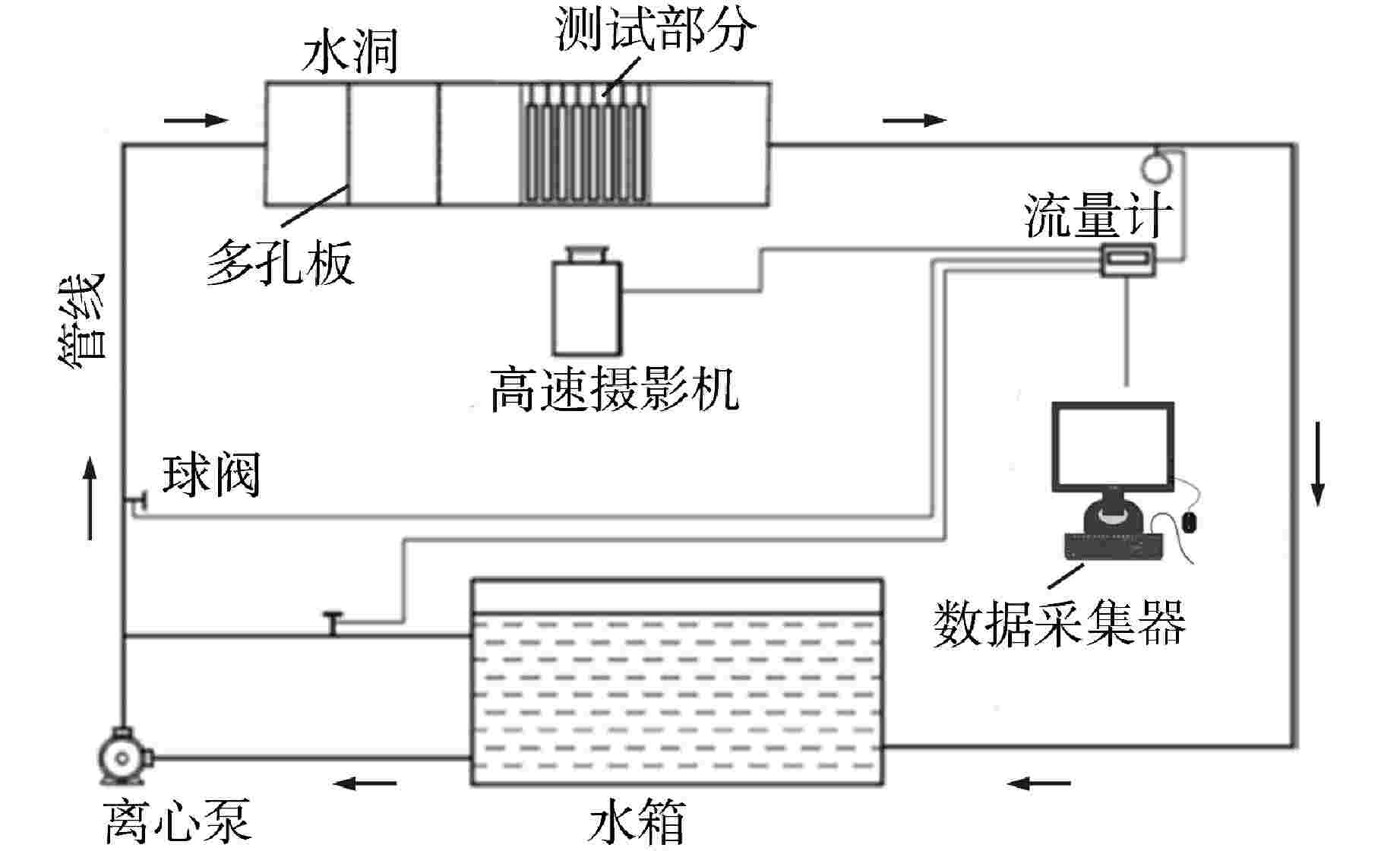
摘要: 针对现有流弹失稳模拟研究中的流固耦合模型存在计算精度较低、计算成本巨大的问题,建立了一种可以预测管束临界流速的二维单向流固耦合模型,该模型基于商用ANSYS Fluent软件,通过SST k-ω湍流模型进行流场计算,再由自编译的用户自定义函数(UDF)提取管子所受的流体力,并利用4阶Runge-Kutta法求解结构动力学方程实现单向流固耦合计算。利用该模型对节径比为1.5的转角三角形排布管束进行了流固耦合计算,得到了中心管的临界流速、振幅时程曲线及振幅频谱图,并通过水洞实验进行了验证。结果表明,本模型以较低的计算成本准确地预测了临界流速,同时也获取了管子真实的振动特征,模拟计算的中心管振幅时程曲线及振幅频谱均与实验相近。此外,模拟计算获取的阻力和升力系数数据表明,随着流速增大,阻力和升力系数时程曲线经历了从紊乱到规律的变化,换算流速达到2.44时,阻力和升力系数主频包含管子在静水中固有频率的成分。Abstract: In view of the low calculation accuracy and huge calculation cost of the existing fluid-solid coupling model in the simulation study of fluid-elastic instability, a two-dimensional unidirectional fluid-solid coupling model which can predict the critical velocity of tube bundle is established. This model is based on the commercial ANSYS Fluent software, the flow field is calculated by the SST k-ω turbulence model, and then the fluid force on the tube is extracted by a self-compiled user-defined function (UDF), and the fourth-order Runge-Kutta method is used to solve the structural dynamic equation and realize the unidirectional fluid-solid coupling calculation. Using this model, the fluid-solid coupling calculation is carried out on the triangularly-arranged tube bundle with a pitch-diameter ratio of 1.5, and the critical velocity, the amplitude time-history curve and the amplitude spectrum of the central tube are obtained, which are verified by water tunnel experiments.The results show that this model can accurately predict the critical velocity with low calculation cost, and also obtain the true vibration characteristics of the tube. The amplitude time-history curve and amplitude spectrum of the central tube calculated by simulation are similar to those of the experiment.In addition, the resistance and lift coefficient data obtained by simulation calculation show that the resistance and lift coefficient time-history curves change from disorder to regularity with the increase of the velocity. When the converted velocity reaches 2.44, the main frequency of the resistance and lift coefficient includes the component of the natural frequency of the tube in still water.
-
Key words:
- Fluid-elastic instability /
- Tube bundle /
- Fluid-solid coupling /
- Critical velocity
-
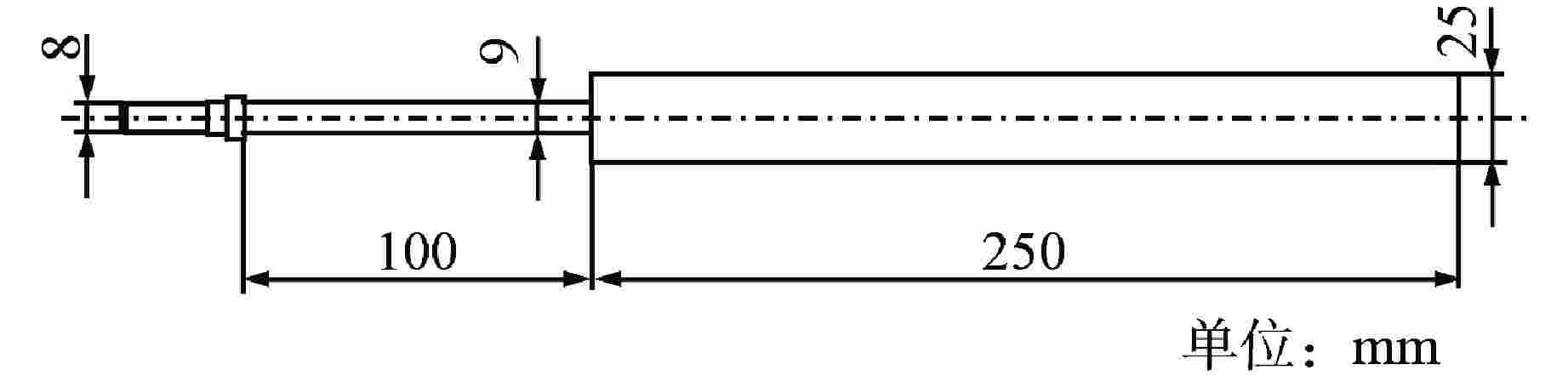
表 1 中心管的结构参数
Table 1. Structural Parameters of the Central Tube
参数名 参数值 直径(D)/m 0.025 单位长度质量(m)/kg 1.348 阻尼(c)/(N·s·m−1) 0.40 质量阻尼参数 0.18 刚度(k)/(N·m−1) 16486.50 静水中的固有频率(${f_{{\text{n,water}}}}$)/Hz 17.61 -
[1] 聂清德, 谭蔚. 管壳式换热器流体诱发振动[M]. 北京: 中国石化出版社, 2014: 1-120. [2] 王聪,陆道纲,曹琼,等. 传热管流致振动设计准则比较[J]. 原子能科学技术,2019, 53(8): 1433-1438. doi: 10.7538/yzk.2019.youxian.0040 [3] BLEVINS R D. Non-proprietary application of ASME code section III, appendix N, to SONGS replacement steam generators[C]//Proceedings of ASME 2017 Pressure Vessels and Piping Conference. Waikoloa: ASME, 2017. [4] LONGATTE E, BENDJEDDOU Z, SOULI M. Methods for numerical study of tube bundle vibrations in cross-flows[J]. Journal of Fluids and Structures, 2003, 18(5): 513-528. doi: 10.1016/j.jfluidstructs.2003.08.010 [5] WANG P F, ZHAO W S, JIANG J, et al. Experimental and numerical investigations of flow-induced vibration of tube arrays subjected to cross flow[J]. International Journal of Pressure Vessels and Piping, 2019, 176: 103956. doi: 10.1016/j.ijpvp.2019.103956 [6] ZHAO W S, XUE F, SHU G G, et al. Analysis of flow-induced vibration of steam generator tubes subjected to cross flow[J]. Nuclear Engineering and Design, 2014, 275: 375-381. doi: 10.1016/j.nucengdes.2014.05.029 [7] 陈小阁. 流体诱发管束振动的流体弹性不稳定性研究[D]. 杭州: 浙江大学, 2017. [8] TANG D, BAO S Y, LUO L J, et al. A CFD/CSD coupled method with high order and its applications in flow induced vibrations of tube arrays in cross flow[J]. Annals of Nuclear Energy, 2019, 130: 347-356. doi: 10.1016/j.anucene.2019.03.003 [9] 吴皓,谭蔚,聂清德. 正方形排布管束流体弹性不稳定性数值计算模型研究[J]. 振动与冲击,2013, 32(21): 102-106. doi: 10.3969/j.issn.1000-3835.2013.21.018 [10] 刘丽艳,石凯,徐炜,等. 同心圆排布管束流体弹性不稳定性模拟研究[J]. 压力容器,2019, 36(5): 29-34. doi: 10.3969/j.issn.1001-4837.2019.05.005 [11] TAN W, LI Z, WU H, et al. Experiment study on fluidelastic instability of tube bundles consisting of different frequency tubes with visual image processing system[J]. Journal of Pressure Vessel Technology, 2018, 140(3): 031302. doi: 10.1115/1.4039454 [12] Hassan M, Gerber A, Omar H. Numerical Estimation of Fluidelastic Instability in Tube Arrays[J]. Journal of Pressure Vessel Technology, 2010, 132(4): 269-278. [13] 刘建,张毅雄,冯志鹏,等. 正三角形排列管束结构流弹失稳流体力模型数值研究[J]. 应用数学和力学,2020, 41(5): 499-508. -





 下载:
下载: