COSINE程序再淹没模型验证及参数敏感性分析

李雪琳; 张昊; 杨燕华

doi:10.13832/j.jnpe.2022.06.0073

COSINE程序再淹没模型验证及参数敏感性分析

doi: 10.13832/j.jnpe.2022.06.0073

上海交通大学核科学与工程学院，上海，200240

详细信息

作者简介:
李雪琳（1996—），女，硕士研究生，现主要从事COSINE程序验证及不确定性分析研究工作，E-mail: listening_lxl@sjtu.edu.cn

中图分类号: TL364
计量
- 文章访问数: 211
- HTML全文浏览量: 96
- PDF下载量: 37
- 被引次数: 0
出版历程
- 收稿日期: 2021-11-08
- 修回日期: 2021-12-08
- 刊出日期: 2022-12-14

Verification of COSINE Reflooding Model and Sensitivity Analysis of Parameters

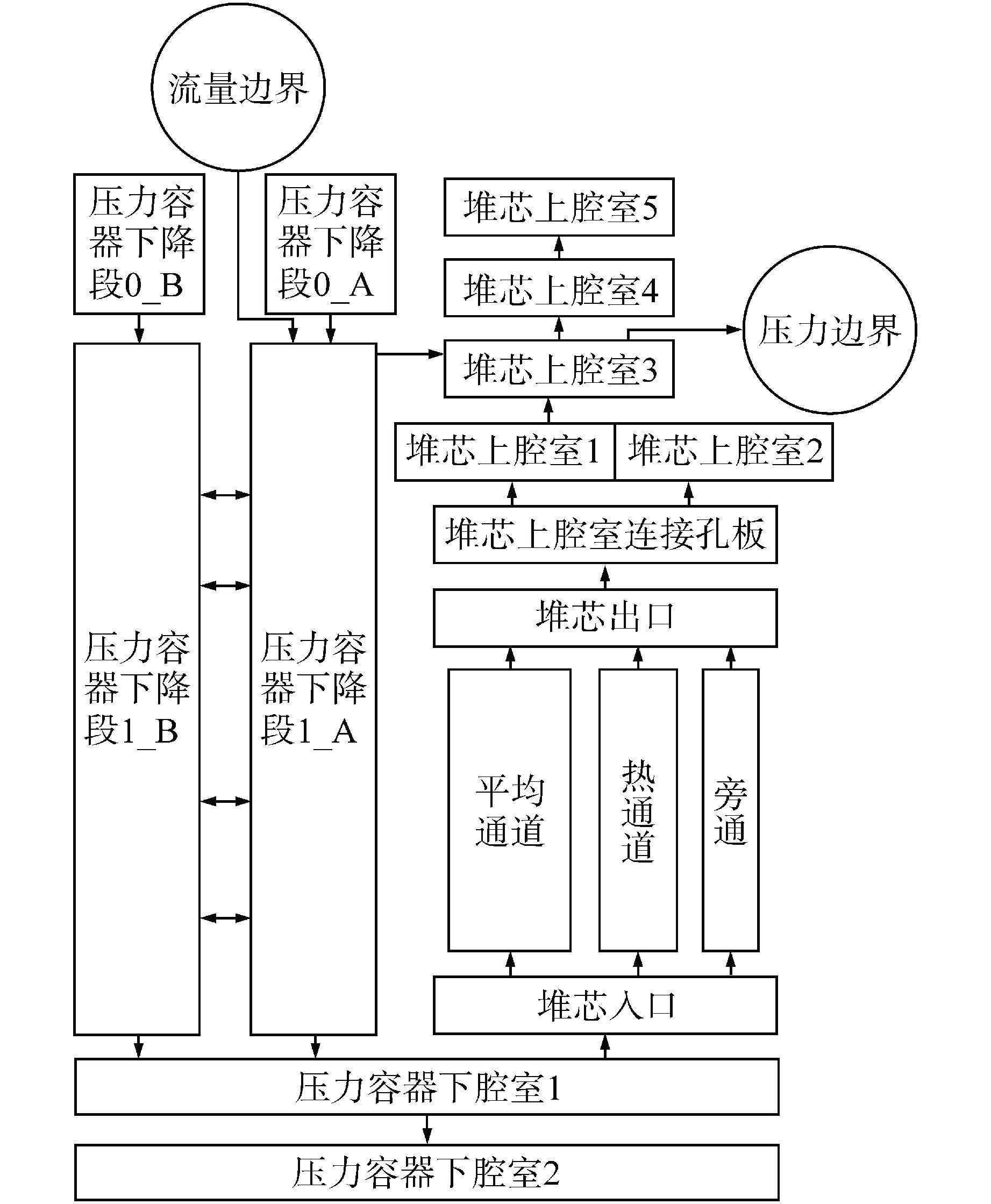
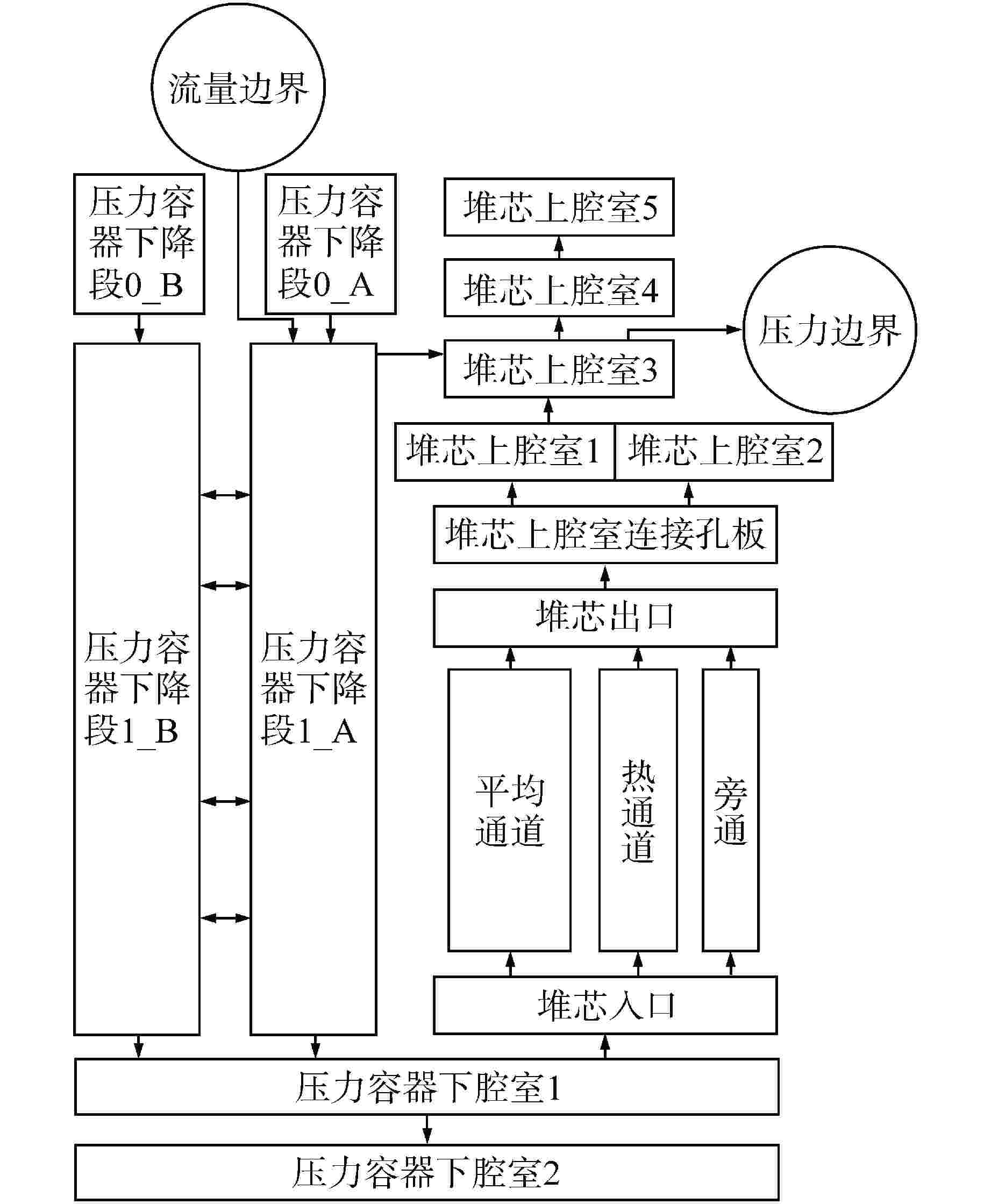
School of Nuclear Science and Engineering, Shanghai Jiaotong University, Shanghai, 200240, China

摘要

摘要: 再淹没是压水堆大破口失水事故后的重要阶段，为评估系统程序在该阶段的计算能力，需要选择多种传热模型对失水事故进行复现并分析参数的敏感性响应。本文对压水堆失水事故实验（LOFT）台架进行建模，将COSINE程序中不同传热模型的计算结果与实验数据比较，验证了传热模型精确度；同时进行再淹没阶段的参数敏感性计算，识别出了对第二包壳峰值温度（PCT）影响最大的参数。计算表明：COSINE程序的传热模型能较好地预测再淹没现象；对计算结果影响较大的敏感性参数包括：UO₂体积热容、液滴直径、液滴相间传热系数和膜态沸腾壁面对汽相的传热系数。
- 再淹没 /
- 敏感性分析 /
- COSINE /
- LOFT实验
Abstract: Reflooding is an important stage after the PWR large break accident. In order to evaluate the calculation capability of the system program at this stage, it is necessary to select a variety of heat transfer models to reproduce the accident and analyze the sensitivity response of the parameters. In this paper, the PWR Loss of Fluid Test (LOFT) bench is modeled, and the calculation results of different heat transfer models in the COSINE program are compared with the experimental data to verify the accuracy of the model; At the same time, the parameter sensitivity calculation in the reflooding stage is carried out, and the parameters which have the greatest influence on the second peak cladding temperature (PCT) are identified. The calculation shows that the heat transfer model of COSINE program can well predict the reflooding phenomenon, and the sensitivity parameters that have great influence on the calculation results include UO₂ volume heat capacity, droplet diameter, droplet interphase heat transfer coefficient and heat transfer coefficient of film boiling wall against vapor phase.
- Reflooding /
- Sensitivity analysis /
- COSINE /
- LOFT experiment

HTML全文

图 1 LOFT压力容器

Figure 1. LOFT Pressure Vessel

下载: 全尺寸图片幻灯片

图 2 不同Bromley修正式预测的堆芯水装量变化

Figure 2. Changes of Core Water Loading Predicted by Different Bromley Modified Corrections

下载: 全尺寸图片幻灯片

图 3 不同Bromley修正式预测的热点处包壳温度变化情况　　　　　　

Figure 3. Changes of Cladding Temperature at Hot Spot Predicted by Different Bromley Corrections

下载: 全尺寸图片幻灯片

图 4 不同膜态沸腾传热关系式预测的包壳温度变化

Figure 4. Changes of Cladding Temperature Predicted by Different Film Boiling Heat Transfer Relations

下载: 全尺寸图片幻灯片

图 5 根据参数上下限计算得到的PCT变化

Figure 5. Calculated PCT Variance Based on Upper/Lower Limits of Parameters

下载: 全尺寸图片幻灯片

图 6 敏感参数与PCT的Spearman相关系数

Figure 6. Spearman Coefficients of Sensitive Parameters and PCT　　　　　

下载: 全尺寸图片幻灯片

表 1 COSINE程序的再淹没膜态沸腾传热模型

Table 1. Heat Transfer Model of Reflooding Film Boiling in COSINE Program

传热方式	模型		传热关系式	修正项
汽膜导热	Bromley^[8]	Bromley_modify1	${h_{ {\text{bromley} } } } = 0.62{\left[ {\dfrac{ { {k_{\text{v} } ^3}g{\rho _{\text{v} } }{h_{ {\text{fg} } } }\Delta \rho } }{ { {\mu _{\text{v} } }L'\Delta T} } } \right]^{0.25} }$	$L' = 2{\text{π } }{\left[ {\dfrac{\sigma }{ {g({\rho _{_{\text{l} }} } - {\rho _{\text{v} } })} } } \right]^{0.25} }$
		Bromley_modify2	${h_{ {\text{mod2} } } } = 0.62{\left[ {\dfrac{ { {k_{\text{v} } ^3}g{\rho _{\text{v} } }{ {h'_{ {\text{fg}} } } }\Delta \rho } }{ { {\mu _{\text{v} } }L'\Delta T} } } \right]^{0.25} }$	L′、${h'_{ {\text{fg} } } } = {h_{ {\text{fg} } } } + 0.5{c_{ { {p,\text{v}} } } }\Delta T$$ {h'_{{\text{fg}}}} $
		Bromley_modify3	$\begin{gathered} {h_{ {\text{mod3} } } } = {\alpha _{ {\text{spfit,v} } } }{h_{ {\text{bromley} } } }(L',{h_{ {\text{fg} } } ^\prime} ) \times \\ {\text{ } }[1 + 0.025\max ({T_{ {\text{sat} } } } - {T_{\text{l} } }),0.01] \\ \end{gathered}$	L′、$ {h'_{{\text{fg}}}} $、α_spfit,v、液体过冷修正$ h' = h[1 + 0.025\max ({T_{{\text{sat}}}} - {T_{\text{l}}}),0.01] $
		Bromley_modify4	${h_{ {\text{mod4} } } } = {\alpha_{_{\text{l} }} }{h_{ {\text{bromley} } } }(L',{h_{ {\text{fg} } } ^\prime })$	$L'、 {h'_{{\text{fg}}}} $、α_l
	Berenson^[9]		${h_{ {\text{Berenson} } } } = 0.425{\left[ {\dfrac{ { {k_{\text{v} } ^3}g{\rho _{\text{v} } }{h_{ {\text{fg} } } }\Delta \rho } }{ { {\mu _{\text{v} } }L'\Delta T} } } \right]^{0.25} }$	L′
	Dougall-Rhosenow^[10]		${h_{ {{{\rm{D}} - {\rm{R}}} } } } = 0.023R{e_{ {\text{Hom} } } ^{0.8}}P{r^{0.4} }$	$ R{e_{{\text{Hom}}}} = \dfrac{{{G_{{\text{mix}}}}D}}{{{\mu _{\text{v}}}}}\left[ {{x_{\text{e}}} + \dfrac{{(1 - {x_{\text{e}}}){\rho _{{\text{sat,v}}}}}}{{{\rho _{{\text{sat,l}}}}}}} \right] $
	Groeneveld^[11-12]	Groeneveld 5.7	${h_{_{ { { {\rm{G} } - 5} }{\text{.7} } }} } = 0.052R{e_{_{ {\text{Hom} }} } ^{0.688} }P{r^{1.26} }{Y^{ - 1.06} }\dfrac{ { {\mu _{\text{v} } } } }{D}$	$Re_{_{\rm{Hom} }}、Y = 1 - 0.1{\left(\dfrac{ { {\rho _{ {\text{sat,l} } } } } }{ { {\rho _{ {\text{sat,v} } } } } } - 1\right)^{0.4} }{(1 - {x_{\text{e} } })^{0.4} }$
	Groeneveld^[11-12]	Groeneveld-Delorme	${h_{_{ { { {\rm{G} }} - {\rm{D} } } } } } = 0.008348R{e_{ {\text{Hom} } } ^{0.8774} }P{r_{\text{f} } ^{0.6112} }\dfrac{ { {\mu _{\text{f} } } } }{D}$	$Re_{\rm{Hom} }、膜温 {T_{\text{f} } } = \dfrac{ { {T_{_{\text{W}} } } + {T_{\text{v} } } }}{2}$
气相对流	Dittus-Boelter		$ {h_{\text{v}}} = 0.023R{e^{0.8}}P{r^{0.4}} $
壁面辐射	Sun-Gonzales Santalo-Tien		${q_{ {\text{w,l} } } } = {F_{ {\text{w,l} } } }{\sigma_{ _{ { { {\rm{S}} } - {\rm{B} } } } } }({T_{\text{w} } ^4} - {T_{ {\text{sat,l} } } ^4})$

下载: 导出CSV

表 2 待分析的重要参数

Table 2. Important Parameters to Be Analyzed

参数分类	参数/编号		系数变化范围
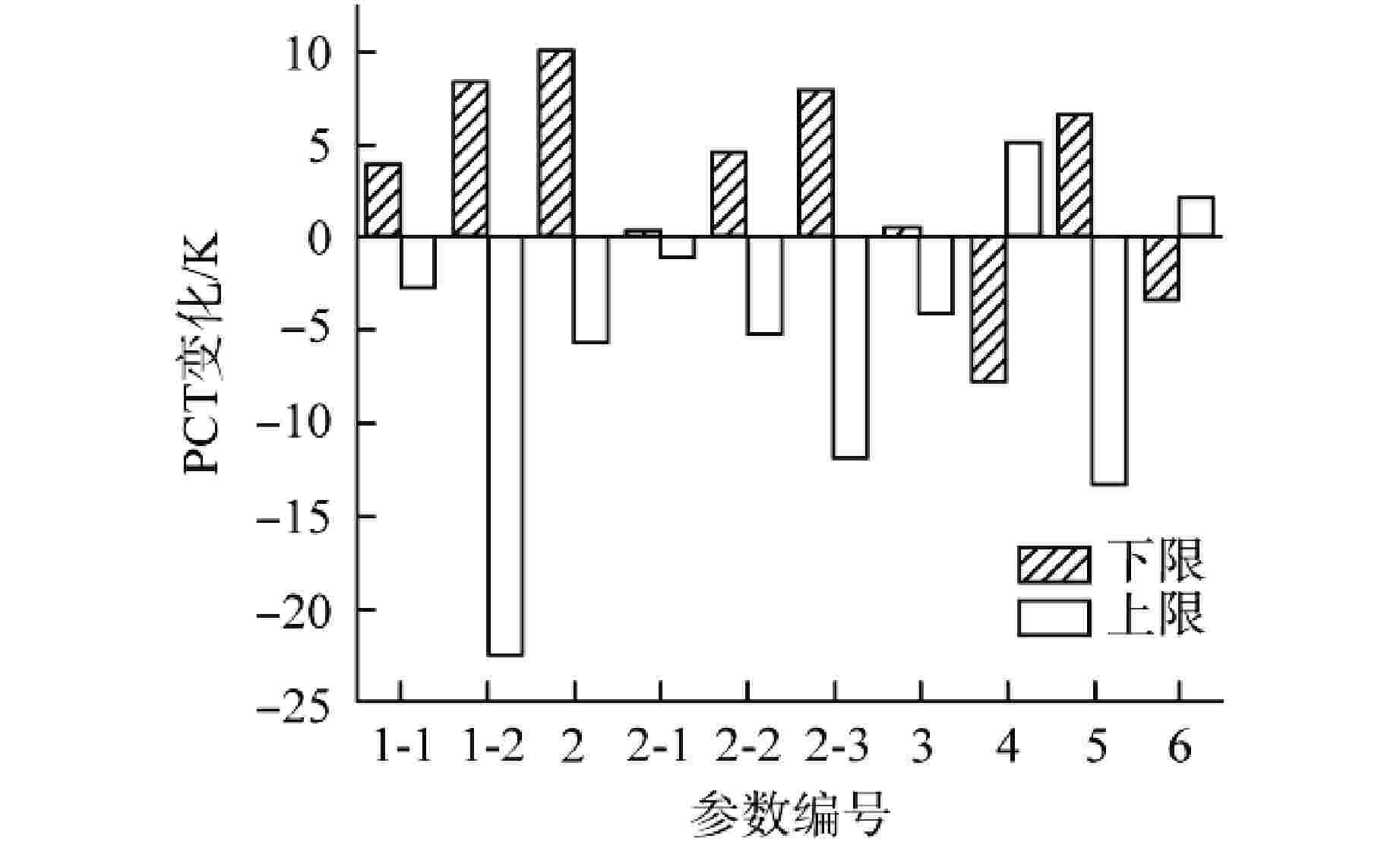
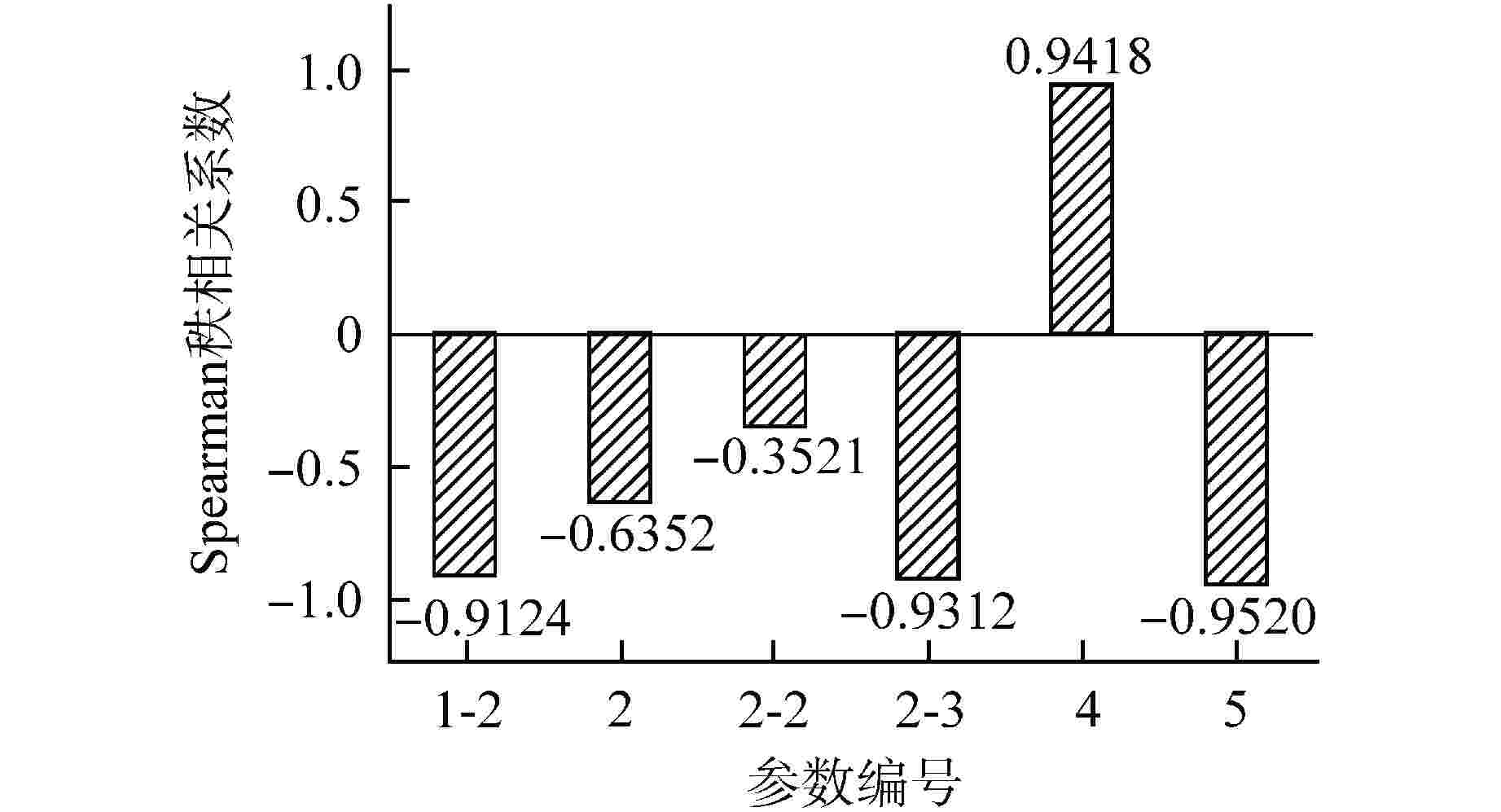
全局模型参数	膜态沸腾传热系数（壁面对液相）/1-1		0.5~3.0
	膜态沸腾传热系数（壁面对汽相）/1-2		0.4~4.0
	相间传热全局系数/2	气泡/2-1	0.2~5.0
		汽膜/2-2
		液滴/2-3
	相间摩擦全局系数/3		0.5~1.5
局部系数参数	液滴直径/4		0.33~2.0
基本参数	UO₂体积热容/5		0.8~1.2
基本参数	进口水温/6		±10 K

下载: 导出CSV

参考文献(16)

[1]	于平安, 朱瑞安, 喻真烷, 等. 核反应堆热工分析[M]. 上海: 上海交通大学出版社, 2002: 236
[2]	李冬,刘晓晶,杨燕华. RELAP5程序再淹没现象物理模型的敏感性分析[J]. 核动力工程,2014, 35(S1): 166-169.
[3]	阮神辉, 杨继涛, 文青龙, 等. 基于RBHT再淹没传热试验的RELAP5/MOD4再淹没计算模型验证研究[C]//第十六届全国反应堆热工流体学术会议暨中核核反应堆热工水力技术重点实验室2019年学术年会. 惠州: 中国科学院近代物理研究所, 2019: 11.
[4]	李永兵. 认证级LOCA分析程序验证及其三维效应的研究[D]. 上海: 上海交通大学, 2009.
[5]	吕莉. 基于RELAP5程序的再淹没膜态沸腾传热模型研究[D]. 衡阳: 南华大学, 2015.
[6]	葛炜,杨燕华,刘飒,等. 大型先进压水堆核电站关键设计软件自主化与COSINE软件包研发[J]. 中国能源,2016, 38(7): 39-44. doi: 10.3969/j.issn.1003-2355.2016.07.007
[7]	PRASSINOS P G, GALUSHA B M, ENGELMAN D B. Experiment data report for LOFT power ascension experiment L2-3: DE-AC07-76ID01570[R]. Washington: U. S. Nuclear Regulatory Commission, U. S. Department of Energy, Idaho Operations Office, 1979.
[8]	BROMLEY L A. Heat transfer in stable film boiling: AECD-2295[R]. Berkeley: University of California, 1948.
[9]	BERENSON P J. Film-boiling heat transfer from a horizontal surface[J]. Journal of Heat Transfer, 1961, 83(3): 351-356. doi: 10.1115/1.3682280
[10]	DOUGALL R S, ROHSENOW W M. Film boiling of the inside of vertical tubes with upward flow of the fluid at low qualities: Report No. 9079-26[R]. United States: Massachusetts Inst. of Tech., 1963.
[11]	GROENEVELD D C, MOECK E O. An investigation of heat transfer in the liquid deficient regime: AECL-3281[R]. Chalk River: Atomic Energy of Canada Ltd., 1969.
[12]	GROENEVELD D C, DELORME G G J. Prediction of thermal non-equilibrium in the post-dryout regime[J]. Nuclear Engineering and Design, 1976, 36(1): 17-26. doi: 10.1016/0029-5493(76)90138-2
[13]	KOVTONYUK A, PETRUZZI A, D'AURIA F. Post-BEMUSE reflood model input uncertainty methods (PREMIUM) benchmark phase II: identification of influential parameters: NEA/CSNI/R(2014)14[Z]. Nuclear Energy Agency of the OECD (NEA), 2015.
[14]	李冬. 最佳估算模型的不确定性量化方法研究及再淹没模型评估的应用[D]. 上海: 上海交通大学, 2017.
[15]	倪超. AP1000核电厂大破口失水事故最佳估算分析建模与不确定性研究[D]. 上海: 上海交通大学, 2011.
[16]	DE CRÉCY A, BAZIN P, GLAESER H, et al. Uncertainty and sensitivity analysis of the LOFT L2-5 test: results of the BEMUSE programme[J]. Nuclear Engineering and Design, 2008, 238(12): 3561-3578. doi: 10.1016/j.nucengdes.2008.06.004