Parameters Sensitivity Analysis and Optimization of High-Temperature Heat Pipe for Heat Pipe Reactor
-
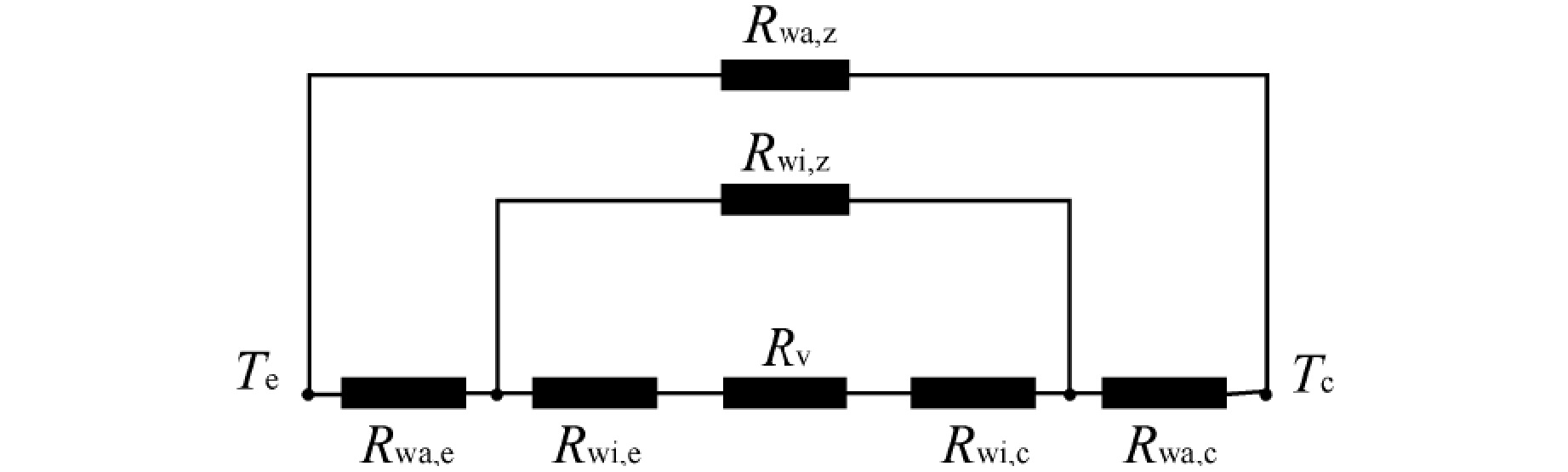
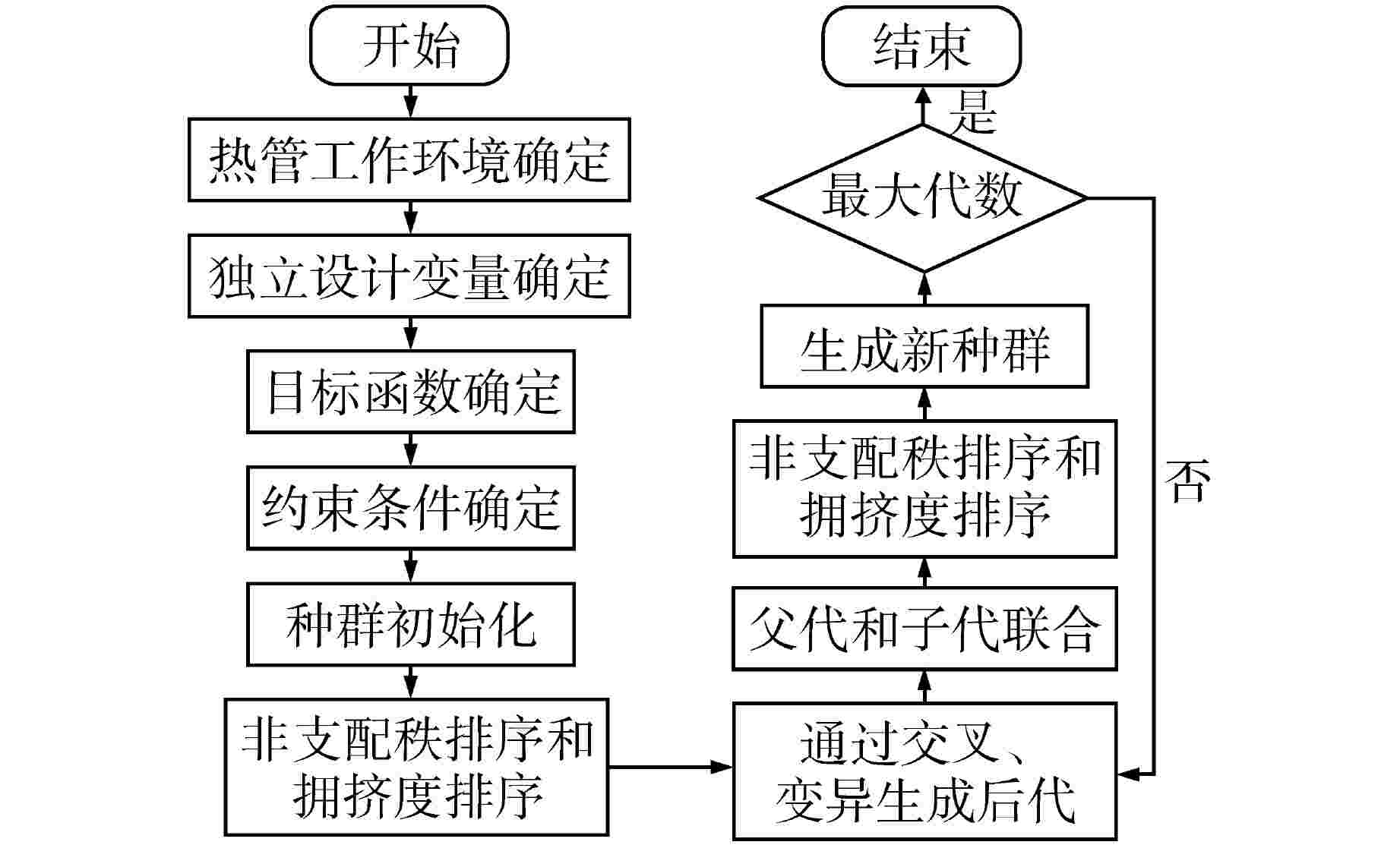
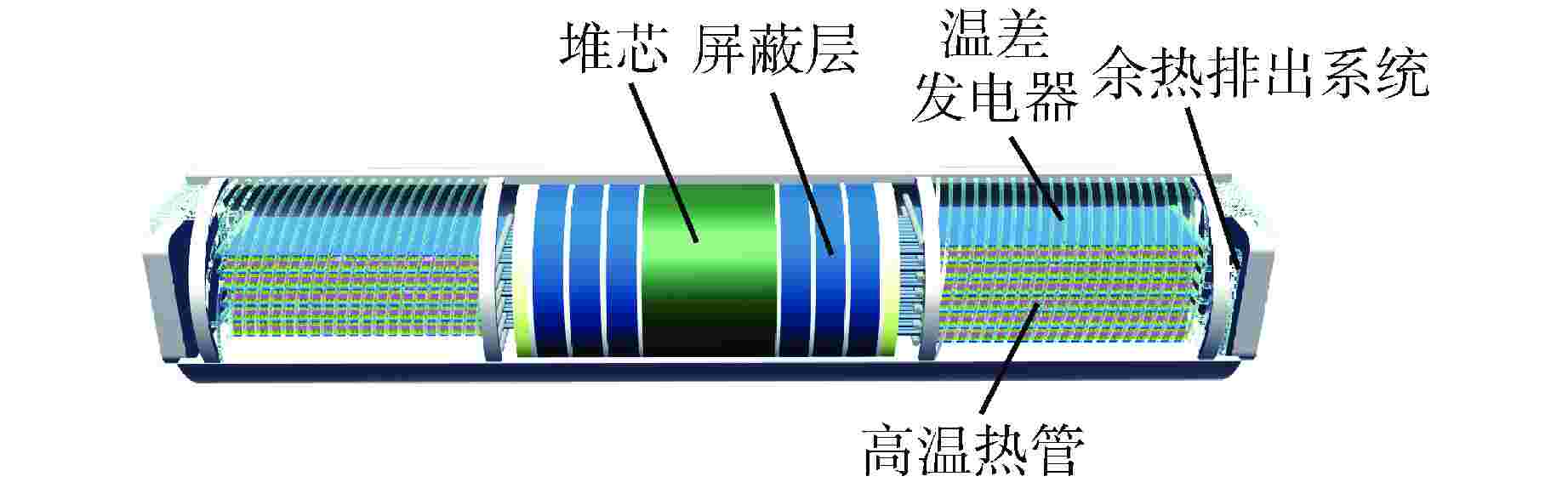
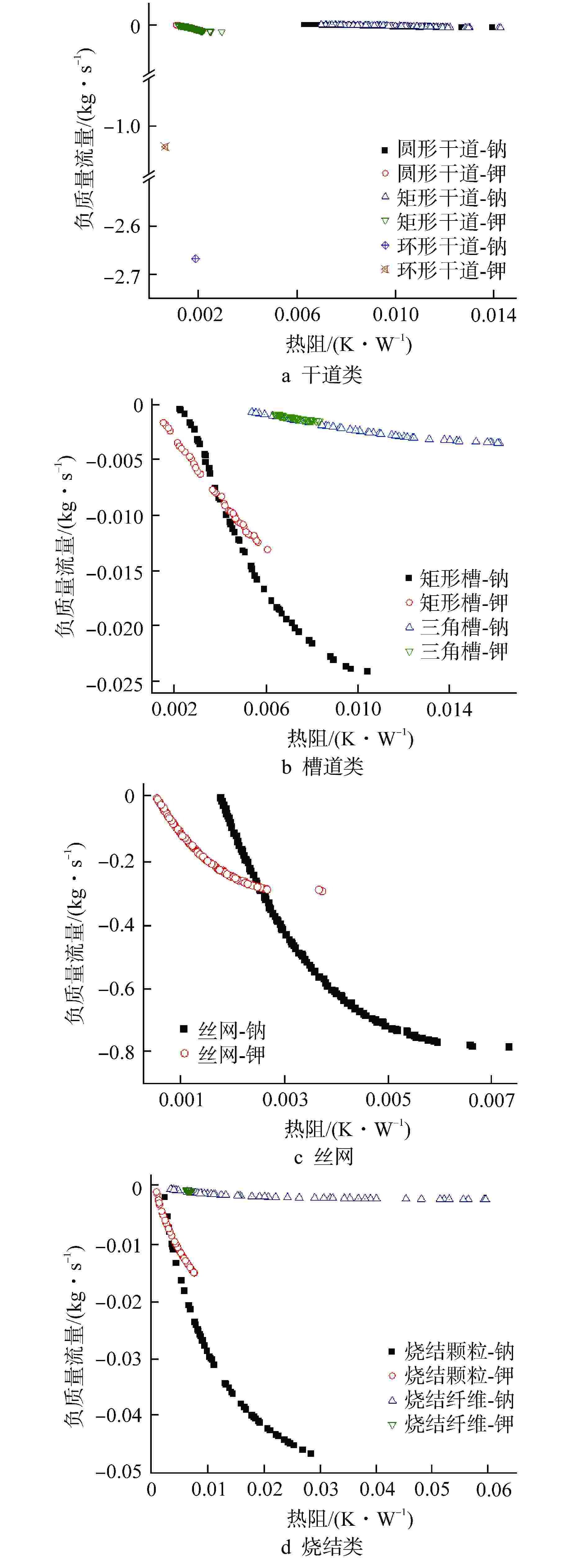
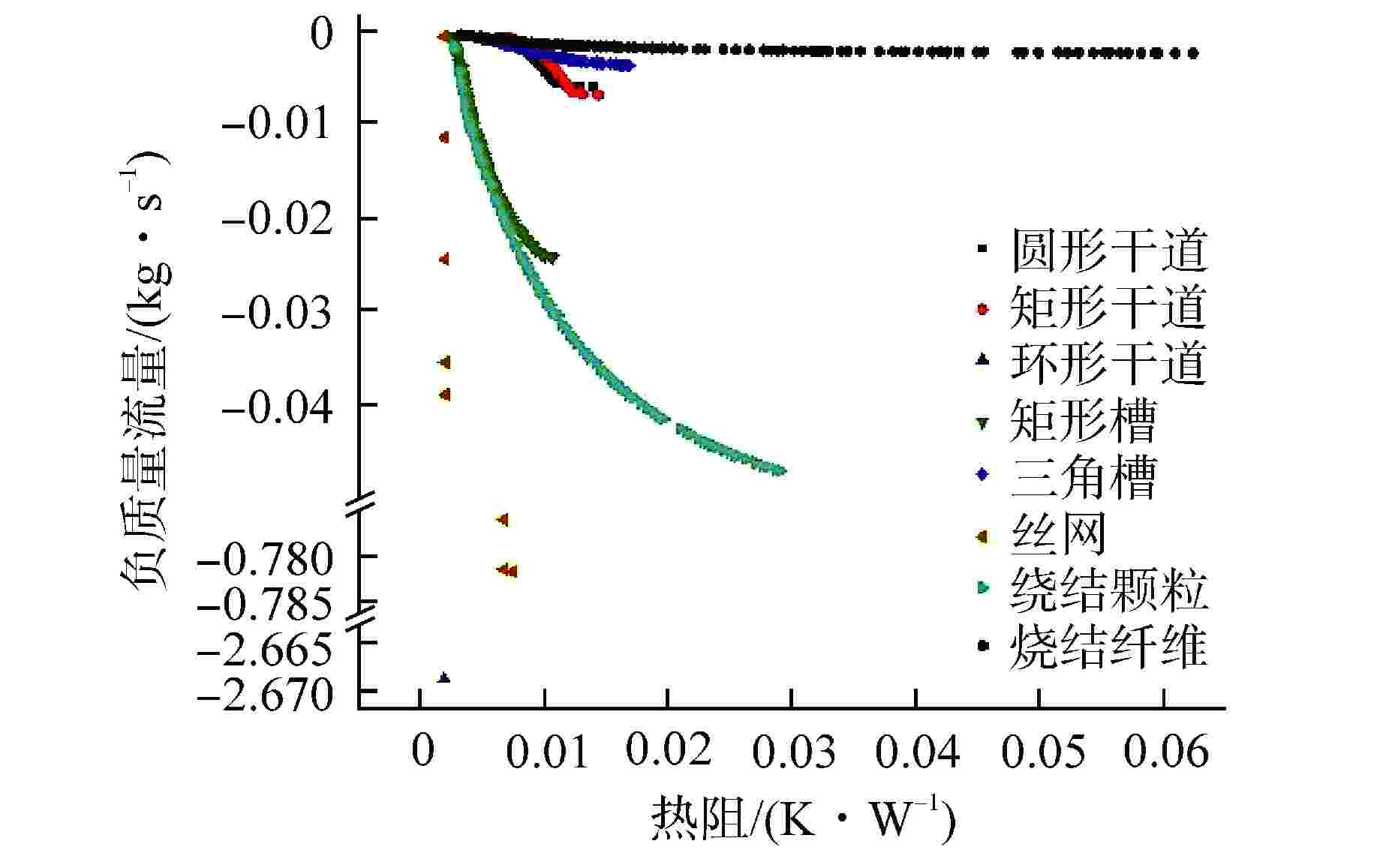
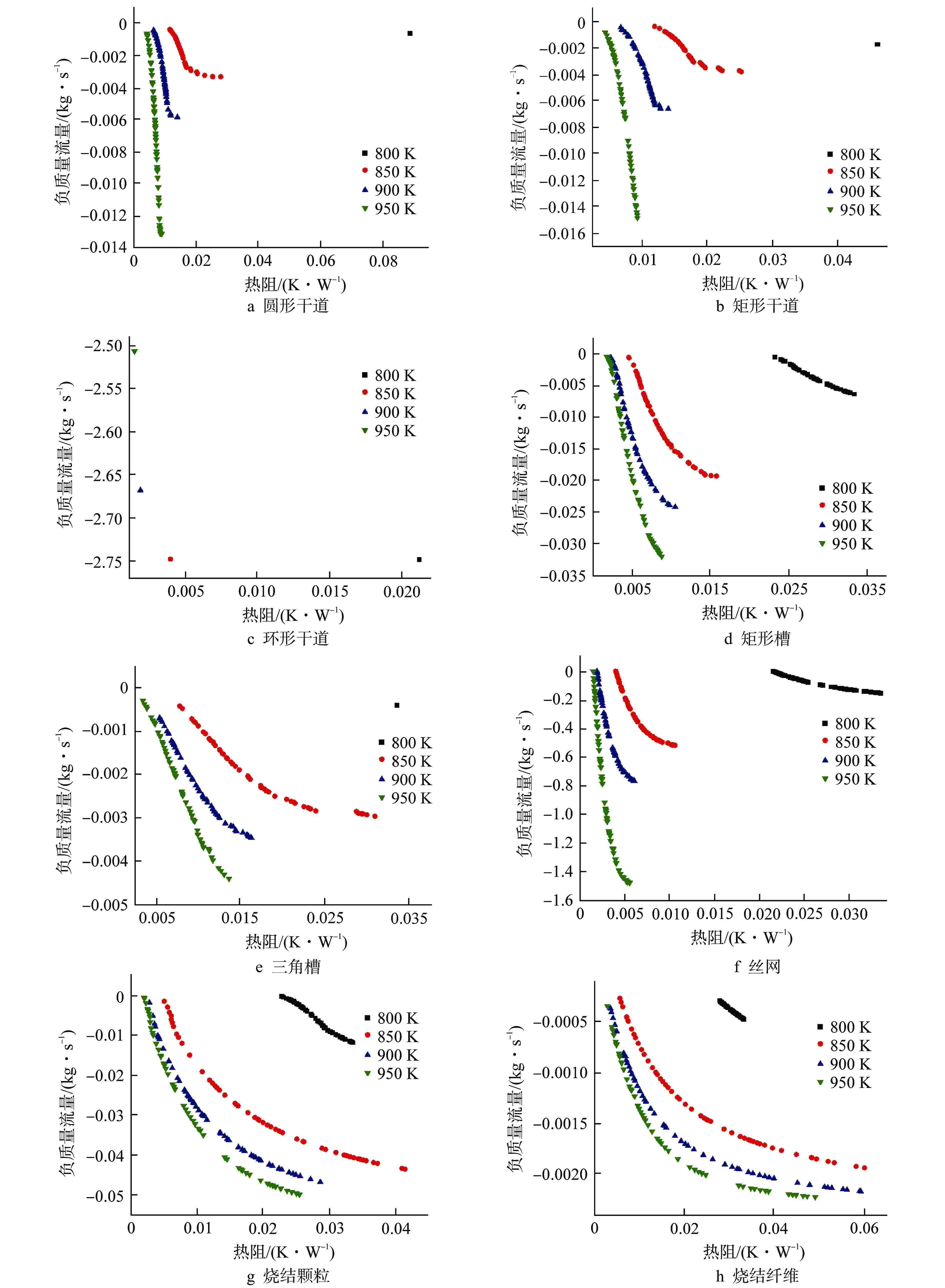
摘要: 热管堆用高温热管的设计是存在约束的多目标优化问题，本文旨在实现高温热管的快速多目标设计优化。针对高温热管，考虑干道、槽道、丝网、烧结等吸液芯，基于改进热阻网络法，采用非支配遗传算法Ⅱ对热阻和毛细质量流量进行优化。结果表明，热管性能与工质和吸液芯有关，圆形和矩形干道采用工质钾更佳，三角槽和烧结纤维采用工质钠更佳；钠热管中热阻性能优劣依次为环形干道、丝网、矩形槽、烧结颗粒、烧结纤维、三角槽、圆形干道、矩形干道，流量性能优劣依次为环形干道、丝网、烧结颗粒、矩形槽、矩形干道、圆形干道、三角槽、烧结纤维；在800~950 K范围内，工作温度提升导致除环形干道外热阻减小89.9%以上，流量增加320.8%以上，环形干道中热阻减小93.5%，但流量减小8.8%。本研究可为核反应堆高温热管设计优化提供参考，提升高温热管性能。Abstract: The design of high-temperature heat pipe for heat pipe reactor is a multi-objective optimization problem with constraints. This paper aims to achieve rapid multi-objective design optimization of high-temperature heat pipe. For high-temperature heat pipe, main line, channel, wire mesh, sintering and other wicks are considered. In this paper, based on the improved thermal resistance network method, the non-dominant genetic algorithm II is used to optimize the thermal resistance and capillary mass flow. The results show that the performance of the heat pipe is related to the working medium and the wick. The working medium potassium is better for round and rectangular main lines, and the working medium sodium is better for triangular grooves and sintered fibers; For thermal resistance in sodium heat pipe, the ranking is in the order of circular main line, wire mesh, rectangular groove, sintered particles, sintered fiber, triangular groove, circular main line and rectangular main line; for flow, the ranking is in the order of circular main line, wire mesh, sintered particles, rectangular groove, rectangular main line, circular main line, triangular groove, sintered fiber. In the range of 800~950 K, the increase of working temperature results in the reduction of thermal resistance by more than 89.9% except for the annular main line, flow increase by more than 320.8%. In the annular main line, the thermal resistance is reduced by 93.5%, but the flow is reduced by 8.8%. This study can provide reference for the design optimization of high-temperature heat pipe of nuclear reactor, and for improving the performance of high-temperature heat pipe.
-
图 2 热管的热阻网络
Rwi,z—dz长度内吸液芯的轴向热阻；Rwi,e/c—蒸发段/冷凝段的吸液芯径向热阻；Rwa,e/c—蒸发段/冷凝段的吸液芯径向热阻；Rwa,z—dz 长度内管壁的轴向热阻；Rv—蒸气热阻；T—温度
Figure 2. Thermal Resistance Network of Heat Pipe
图 3 吸液芯结构示意图
W—槽宽；Dis—槽间距；D—直径；ri—环形干道内半径；ro—环形干道外半径；Df—纤维直径；Dg—槽深；Dp—颗粒直径；ψ—三角槽的1/2角度
Figure 3. Structure Diagram of Wick
图 6 不同吸液芯结构下热阻-负毛细质量流量多目标优化
Figure 6. Multi-objective Optimization of Thermal Resistance-Negative Capillary Mass Flow with Different Wick Structures
图 7 不同吸液芯结构下的热阻和负毛细质量流量
Figure 7. Thermal Resistance and Negative Capillary Mass Flow with Different Wick Structures
图 8 工作温度对钠热管热阻和负质量流量的影响
Figure 8. Influence of Working Temperature on Thermal Resistance and Negative Mass Flow of Sodium Heat Pipe
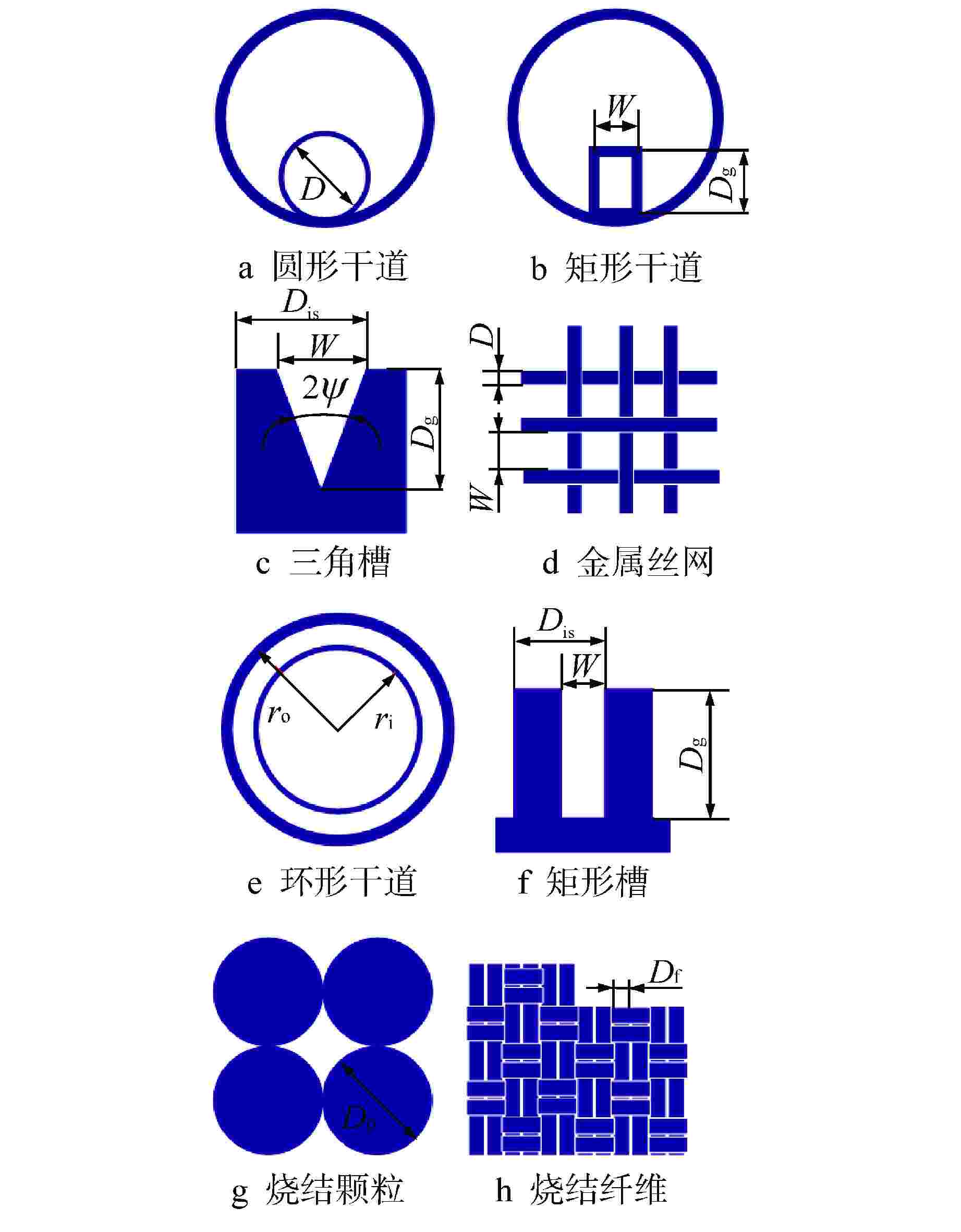
表 1 吸液芯结构特征参数
Table 1. Characteristic Parameters for Wick Structures
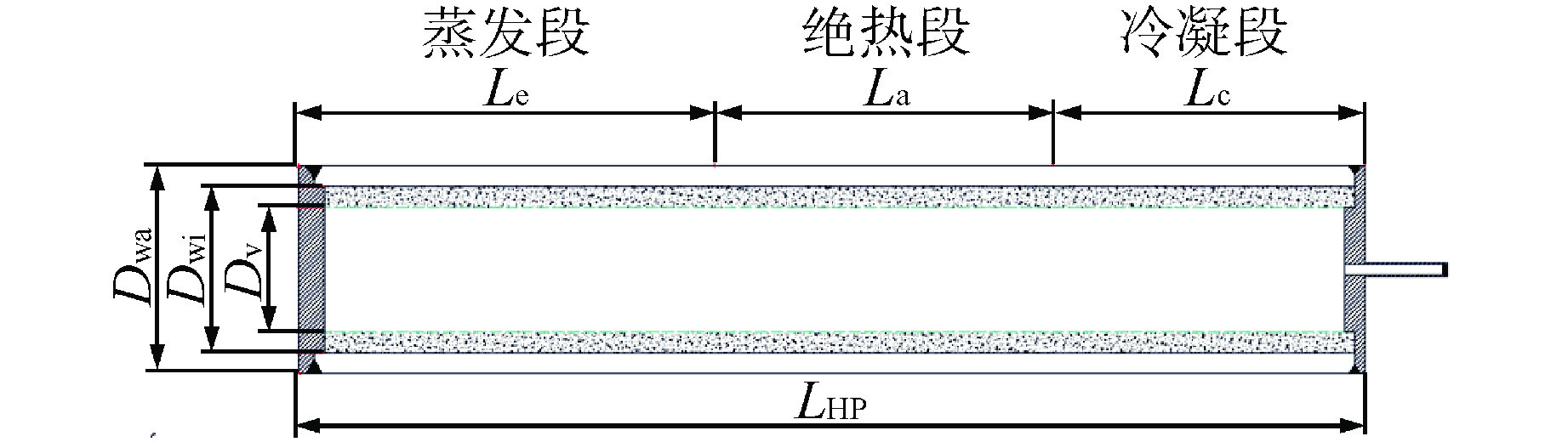
吸液芯结构 rcap Dh ε K 圆形干道 D/2 D 1 D2/32 矩形干道 $ \dfrac{{WDg}}{{W + Dg}} $ $\dfrac{{2WDg}}{{W + Dg}}$ 1 $\dfrac{ {D_{_{\text{h}} }^{^{\text{2} }} } }{ {2{F_{_{ {\text{RA} }} } } } }$ 环形干道 ro−ri 2(ro−ri) 1 $\dfrac{ {D_{_{\text{h} }}^{^{\text{2} }} } }{ {2{F_{_{ {\text{AA} }} } } } }$ 矩形槽 W $ \dfrac{{4WDg}}{{W + 2Dg}} $ $\dfrac{W}{ { {D_{_{ {\text{is} }} } } } }$ $\dfrac{ {\varepsilon D_{_{\text{h} }}^{^{\text{2} }} } }{ {2{F_{_{ {\text{RG} }} } } } }$ 三角槽 $\dfrac{W}{{\cos \psi }}$ $W\cos \psi $ $\dfrac{W}{ {2{D_{_{ {\text{is} }} } } } }$ $\dfrac{ {\varepsilon D_{_{\text{h} }}^{^{\text{2} }} } }{ {2{F_{_{ {\text{IG} } }} } } }$ 丝网 $\dfrac{{W + D}}{2}$ $\dfrac{\varepsilon }{{1 - \varepsilon }}D$ $1 - \dfrac{ {1.05{\text{π } }N_{_{\text{mesh} }} D} }{4}$ $\dfrac{ { {D^{^2}}{\varepsilon ^{^3}} } }{ {122{ {\left( {1 - \varepsilon } \right)}^{^2}} } }$ 烧结颗粒 $0.21{D_{_{\text{p} }} }$ $\dfrac{ {2\varepsilon } }{ {3\left( {1 - \varepsilon } \right)} }{D_{_{\text{p} }} }$ 0.27~0.66 $\dfrac{ {D_{\text{p} }^{^{\text{2}} }{\varepsilon ^{^3}} } }{ {150{ {\left( {1 - \varepsilon } \right)}^{^2}} } }$ 烧结纤维 $\dfrac{ { {D_{_{\text{f} }} } }}{ {2\left( {1 - \varepsilon } \right)} }$ $\dfrac{\varepsilon }{ {1 - \varepsilon } }{D_{_{\text{f} }} }$ 0.6~0.9 FSF Nmesh—丝网目数；FSF、FAA、 FRA、FIG、FRG关系式详见文献[16] 
下载: 导出CSV
表 2 液态金属高温热管设计参数
Table 2. Design Parameters of Liquid-metal Heat Pipe
参数 参数值 参数 参数值 工作温度/K 900 热管长度/m 2.0 最大承受压力/MPa 2 蒸发段长度/m 0.5 工作角度 0°（水平） 冷凝段长度/m 1.0 传热功率/kW 1 管壳外径/mm 30
下载: 导出CSV
表 3 选取钠作为工质时不同吸液芯结构性能比较
Table 3. Comparison of Performance of Various Wick Structures with Sodium as the Working Fluid
性能参数 性能排序 热阻 环形干道>丝网>矩形槽>烧结颗粒>烧结纤维>三角槽>圆形干道>矩形干道 毛细质量流量 环形干道>丝网>烧结颗粒>矩形槽>矩形干道>圆形干道>三角槽>烧结纤维 热阻可行范围 烧结纤维>烧结颗粒>三角槽>矩形槽>圆形干道>矩形干道>丝网>环形干道 毛细质量流量可行范围 丝网>烧结颗粒>矩形槽>矩形干道>圆形干道>三角槽>烧结纤维>环形干道
下载: 导出CSV
-
[1] TIAN Z X, LIU X, WANG C L, et al. Experimental investigation on the heat transfer performance of high-temperature potassium heat pipe for nuclear reactor[J]. Nuclear Engineering and Design, 2021, 378: 111182. doi: 10.1016/j.nucengdes.2021.111182 [2] TIAN Z X, WANG C L, HUANG J L, et al. Code development and analysis on the operation of liquid metal high temperature heat pipes under full condition[J]. Annals of Nuclear Energy, 2021, 160: 108396. doi: 10.1016/j.anucene.2021.108396 [3] FAGHRI A, HARLEY C. Transient lumped heat pipe analyses[J]. Heat Recovery Systems and CHP, 1994, 14(4): 351-363. doi: 10.1016/0890-4332(94)90039-6 [4] ZUO Z J, FAGHRI A. A network thermodynamic analysis of the heat pipe[J]. International Journal of Heat and Mass Transfer, 1998, 41(11): 1473-1484. doi: 10.1016/s0017-9310(97)00220-2 [5] FAGHRI A, BUCHKO M. Experimental and numerical analysis of low-temperature heat pipes with multiple heat sources[J]. Journal of Heat Transfer, 1991, 113(3): 728-734. doi: 10.1115/1.2910624 [6] FAGHRI A. Review and advances in heat pipe science and technology[J]. Journal of Heat Transfer, 2012, 134(12): 123001. doi: 10.1115/1.4007407 [7] CAO Y, FAGHRI A. A numerical analysis of high-temperature heat pipe startup from the frozen state[J]. Journal of Heat Transfer, 1993, 115(1): 247-254. doi: 10.1115/1.2910657 [8] TOURNIER J M, EL-GENK M S. A vapor flow model for analysis of liquid-metal heat pipe startup from a frozen state[J]. International Journal of Heat and Mass Transfer, 1996, 39(18): 3767-3780. doi: 10.1016/0017-9310(96)00066-X [9] TOURNIER J M, EL-GENK M S. A heat pipe transient analysis model[J]. International Journal of Heat and Mass Transfer, 1994, 37(5): 753-762. doi: 10.1016/0017-9310(94)90113-9 [10] TOURNIER J M, EL-GENK M S, JUHASZ A J. Heat-pipe transient model for space applications[J]. AIP Conference Proceedings, 1991, 217(2): 857-868. doi: 10.1063/1.40099 [11] RAJESH V G, RAVINDRAN K P. Optimum heat pipe design: a nonlinear programming approach[J]. International Communications in Heat and Mass Transfer, 1997, 24(3): 371-380. doi: 10.1016/S0735-1933(97)00022-5 [12] SARAFRAZ M M, TLILI I, TIAN Z, et al. Smart optimization of a thermosyphon heat pipe for an evacuated tube solar collector using response surface methodology (RSM)[J]. Physica A:Statistical Mechanics and Its Applications, 2019, 534: 122146. doi: 10.1016/j.physa.2019.122146 [13] DE SOUSA F L, VLASSOV V, RAMOS F M. Generalized extremal optimization for solving complex optimal design problems[C]//Genetic and Evolutionary Computation Conference. Chicago: Springer, 2003: 375-376. [14] RAO R V, MORE K C. Design optimization and analysis of selected thermal devices using self-adaptive Jaya algorithm[J]. Energy Conversion and Management, 2017, 140: 24-35. doi: 10.1016/j.enconman.2017.02.068 [15] RAO R V, MORE K C. Optimal design of the heat pipe using TLBO (teaching-learning-based optimization) algorithm[J]. Energy, 2015, 80: 535-544. doi: 10.1016/j.energy.2014.12.008 [16] FAGHRI A. Heat pipe science and technology[M]. Washington: Taylor & Francis, 1995: 328. [17] 田智星,刘逍,王成龙,等. 高温钾热管稳态运行传热特性研究[J]. 原子能科学技术,2020, 54(10): 1771-1778. [18] 庄骏,张红. 热管技术及其工程应用[J]. 能源研究与利用,2000(5): 41. [19] YUAN S W, FINKELSTEIN A B. Laminar Pipe Flow With Injection and Suction Through a Porous Wall[J]. Transactions of the American Society of Mechanical Engineers, 1956, 78(4): 719-724. [20] CHI S W. Heat pipe theory and practice: a sourcebook[M]. Washington: Hemisphere Pub. Corp., 1976: 188. [21] ZOHURI B. Heat pipe design and technology: a practical approach[M]. Boca Raton: CRC Press, 2011: 96. [22] LEVY E K, CHOU S F. The sonic limit in sodium heat pipes[J]. Journal of Heat Transfer, 1973, 95(2): 218-223. doi: 10.1115/1.3450029 [23] KIM B H, PETERSON G P. Theoretical and physical interpretation of entrainment phenomenon in capillary-driven heat pipes using hydrodynamic instability theories[J]. International Journal of Heat and Mass Transfer, 1994, 37(17): 2647-2660. doi: 10.1016/0017-9310(94)90382-4 [24] CHEN S W, LIU F C, WANG T Y, et al. Modeling and analyses of boiling and capillary limitations for micro channel wick structures[J]. Journal of Mechanics, 2016, 32(3): 357-368. doi: 10.1017/jmech.2015.100 [25] TIEN C L, CHUNG K S. Entrainment limits in heat pipes[J]. AIAA Journal, 1979, 17(6): 643-646. doi: 10.2514/3.61190 [26] RICE J, FAGHRI A. Analysis of porous wick heat pipes, including capillary dry-out limitations[C]//Proceedings of the ASME 2005 International Mechanical Engineering Congress and Exposition. Orlando: ASME, 2005: 595-607. doi: 10.1115/IMECE2005-81456 [27] NODA H, YOSHIOKA K, HAMATAKE T. A model for the heat transfer limit of a screen wick heat pipe[J]. Heat Transfer-Japanese Research, 1989, 18(3): 3118-3123. [28] DOBRAN F. Suppression of the sonic heat transfer limit in high-temperature heat pipes[J]. Journal of Heat Transfer, 1989, 111(3): 605-610. doi: 10.1115/1.3250725 [29] DO K H, KIM S J, GARIMELLA S V. A mathematical model for analyzing the thermal characteristics of a flat micro heat pipe with a grooved wick[J]. International Journal of Heat and Mass Transfer, 2008, 51(19-20): 4637-4650. doi: 10.1016/j.ijheatmasstransfer.2008.02.039 [30] CHENG P, MA H B. A mathematical model predicting the minimum meniscus radius in mixed particles[J]. Journal of Heat Transfer, 2007, 129(3): 391-394. doi: 10.1115/1.2430727 [31] BUSSE C A. Theory of the ultimate heat transfer limit of cylindrical heat pipes[J]. International Journal of Heat and Mass Transfer, 1973, 16(1): 169-186. doi: 10.1016/0017-9310(73)90260-3 [32] PRENGER JR F C, KEMME J E. Performance limits of gravity-assist heat pipes with simple wick structures[M]//REAY D A. Advances in Heat Pipe Technology. Amsterdam: Elsevier, 1982: 137-146. doi: 10.1016/B978-0-08-027284-9.50019-X [33] LEVY E K. Theoretical investigation of heat pipes operating at low vapor pressures[J]. Journal of Engineering for Industry, 1968, 90(4): 547-552. doi: 10.1115/1.3604687 [34] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. doi: 10.1109/4235.996017 -
图(8) / 表(3)
计量
- 文章访问数: 386
- HTML全文浏览量: 121
- PDF下载量: 48
- 被引次数: 0
