Study on Core Power Control of Small Lead-Bismuth Cooled Fast Reactor
-
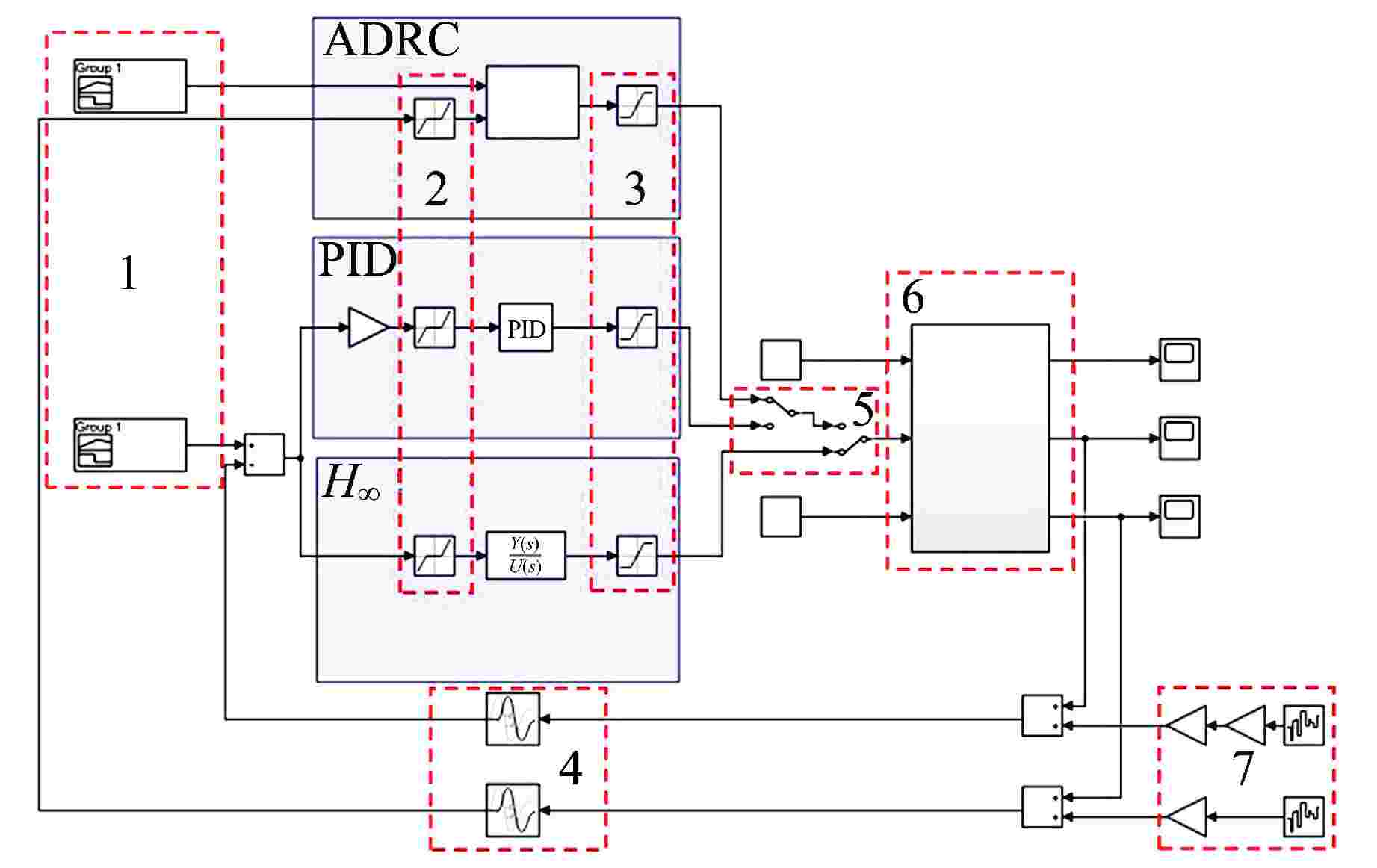
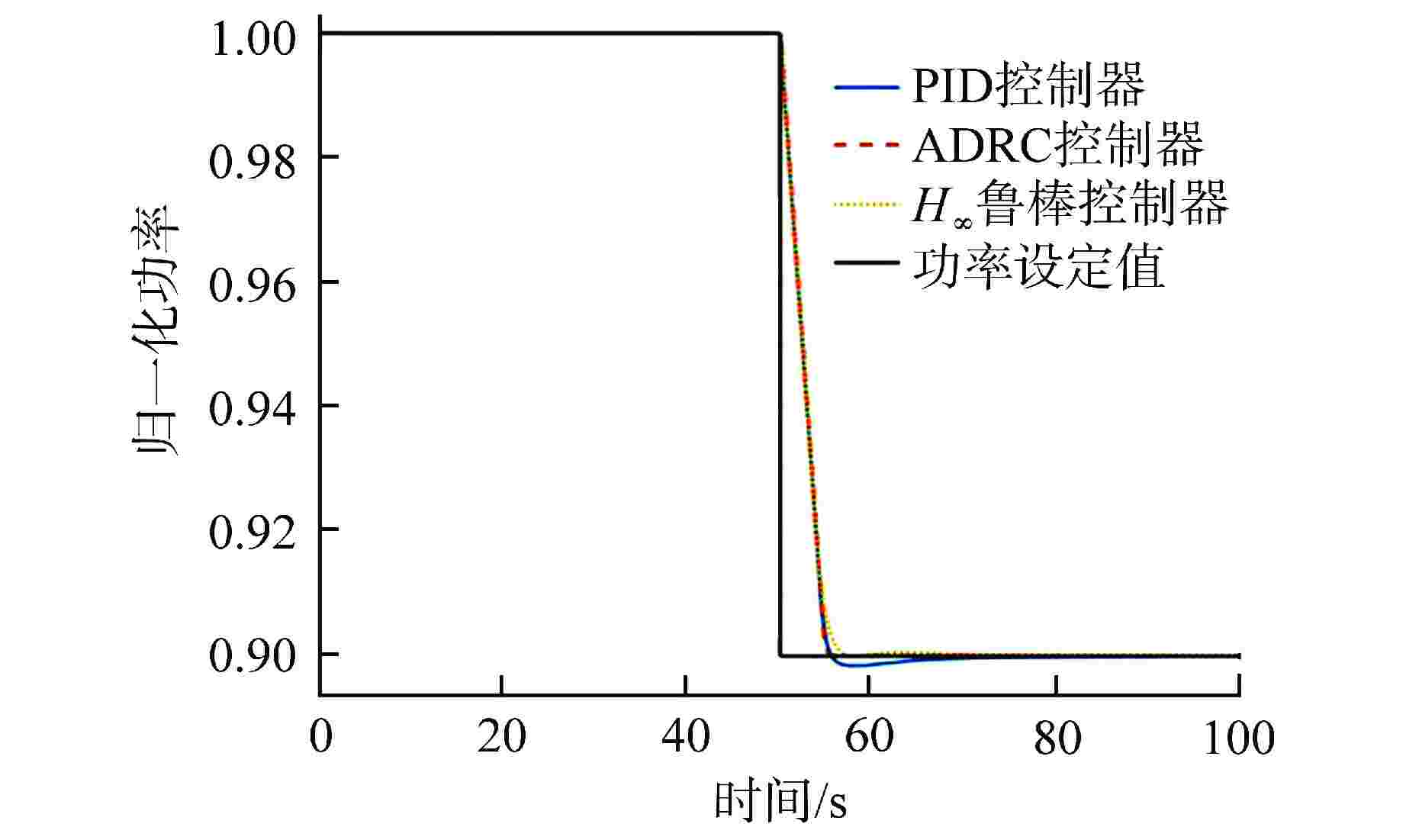
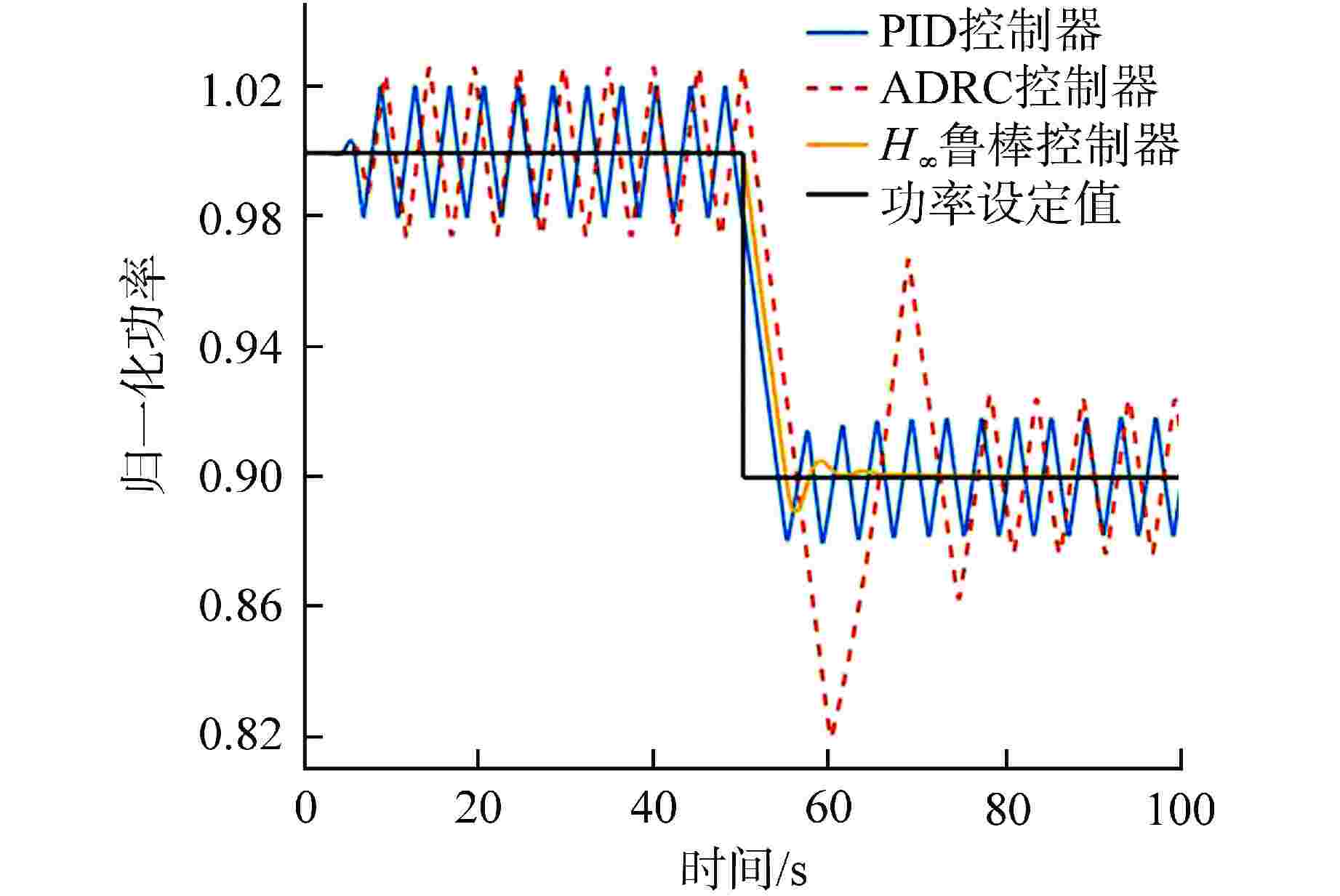
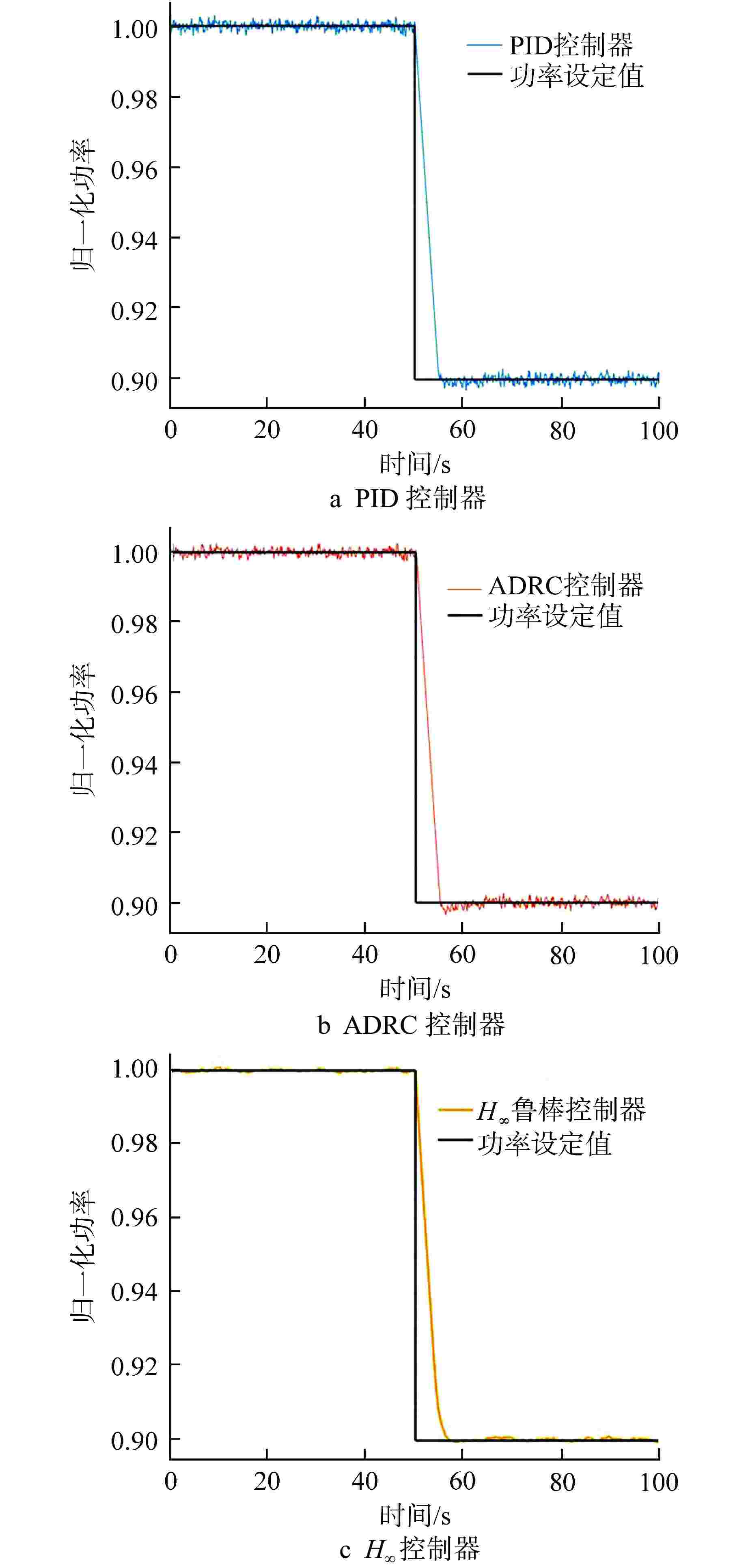
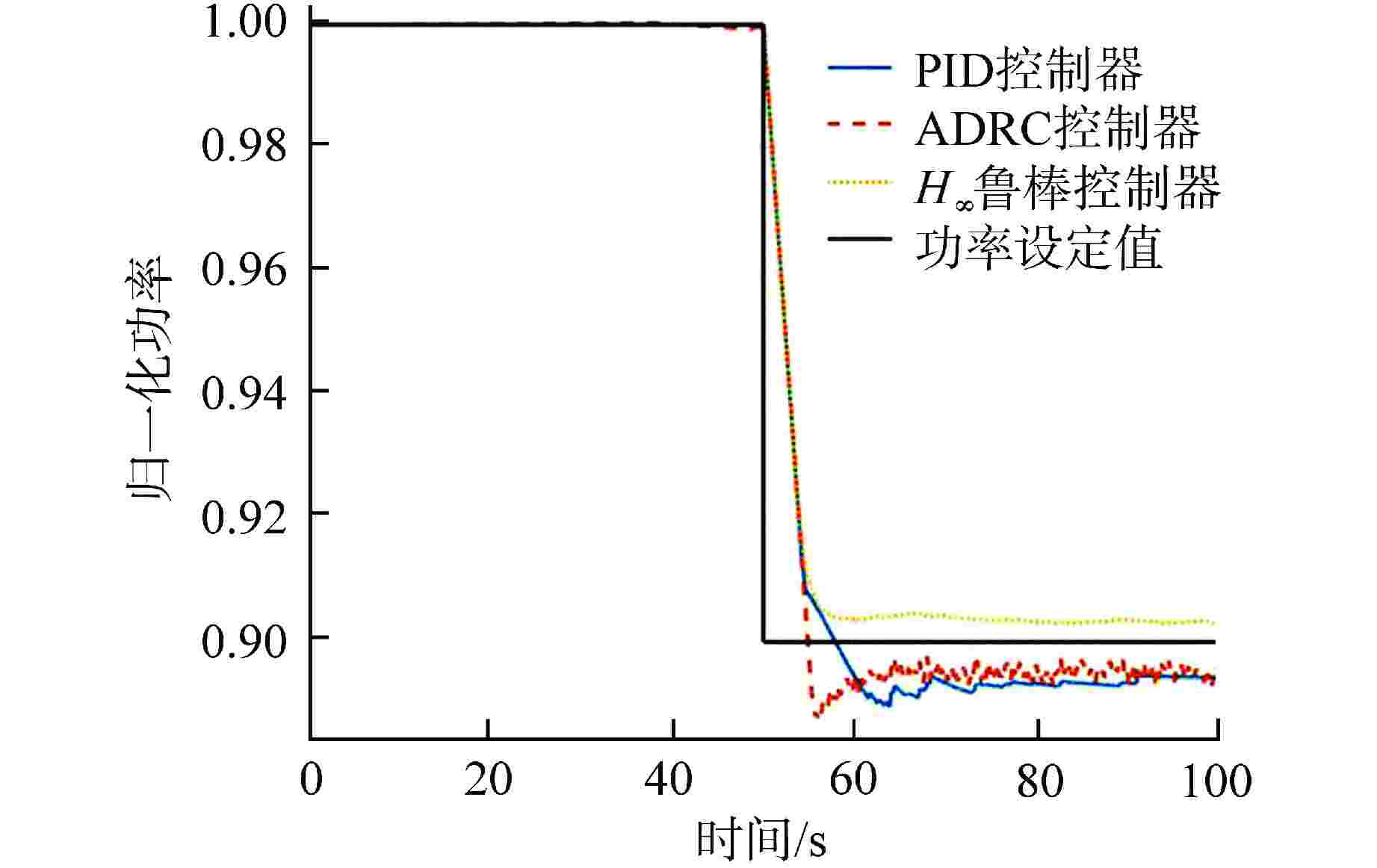
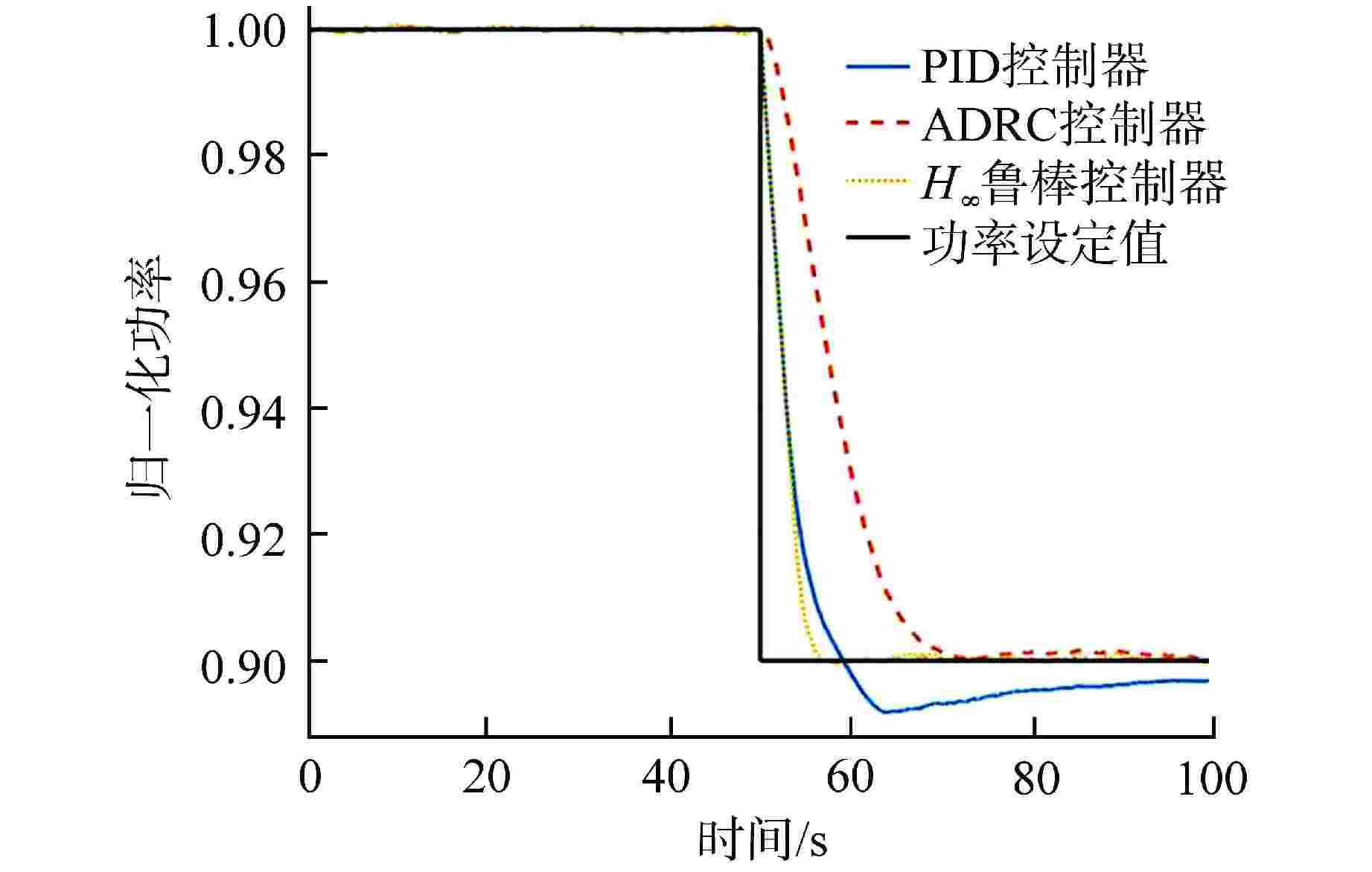
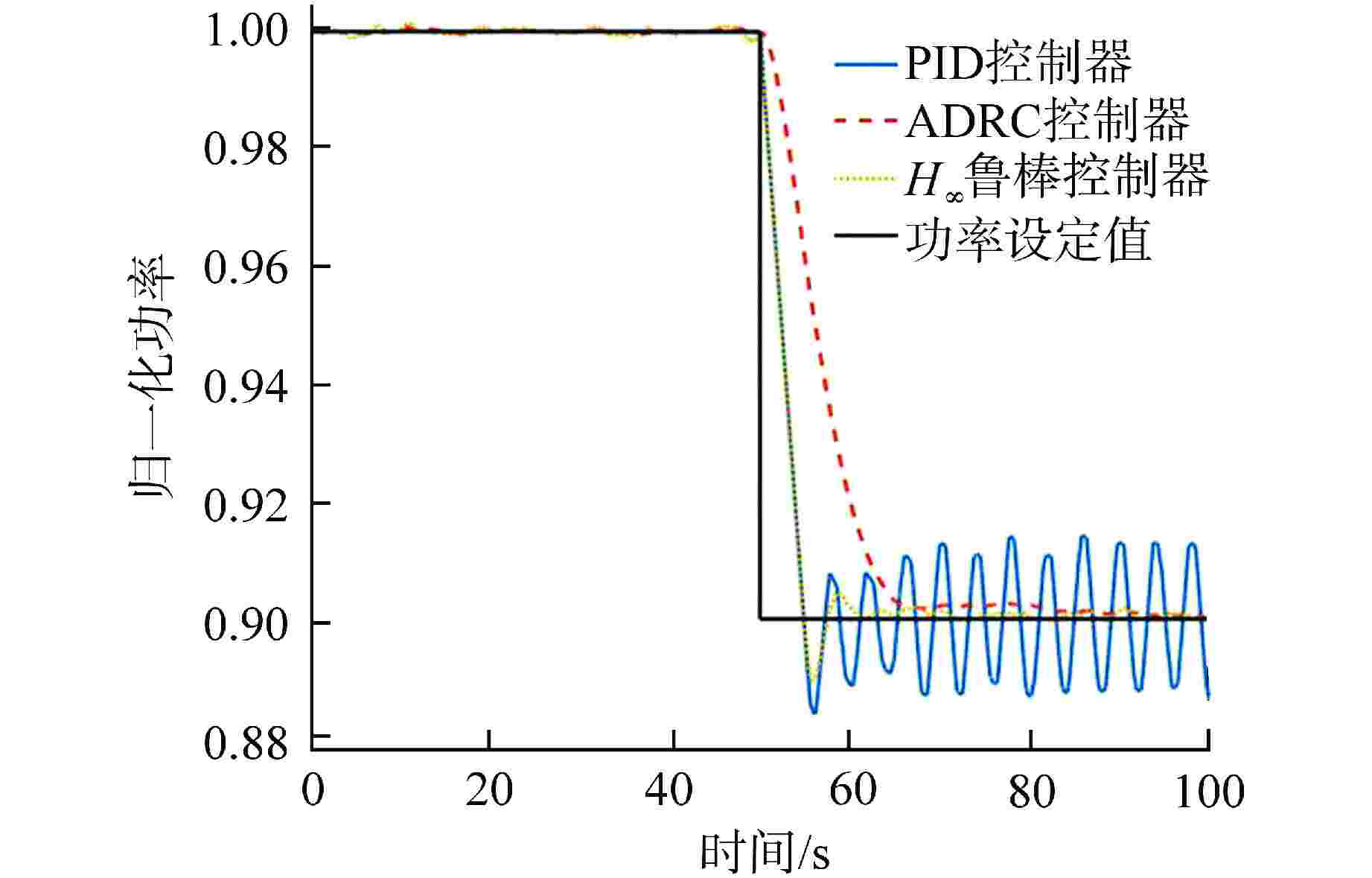
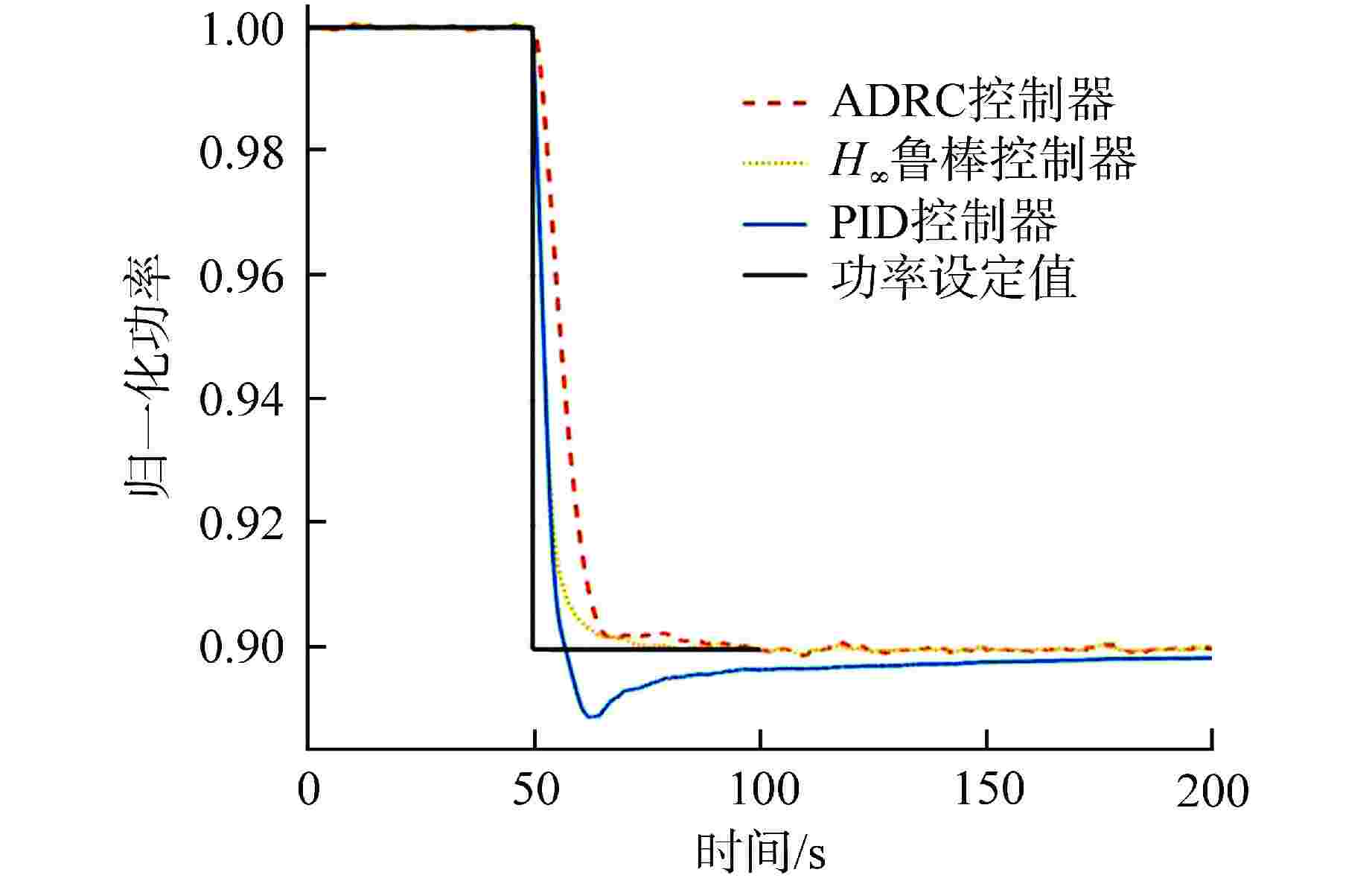
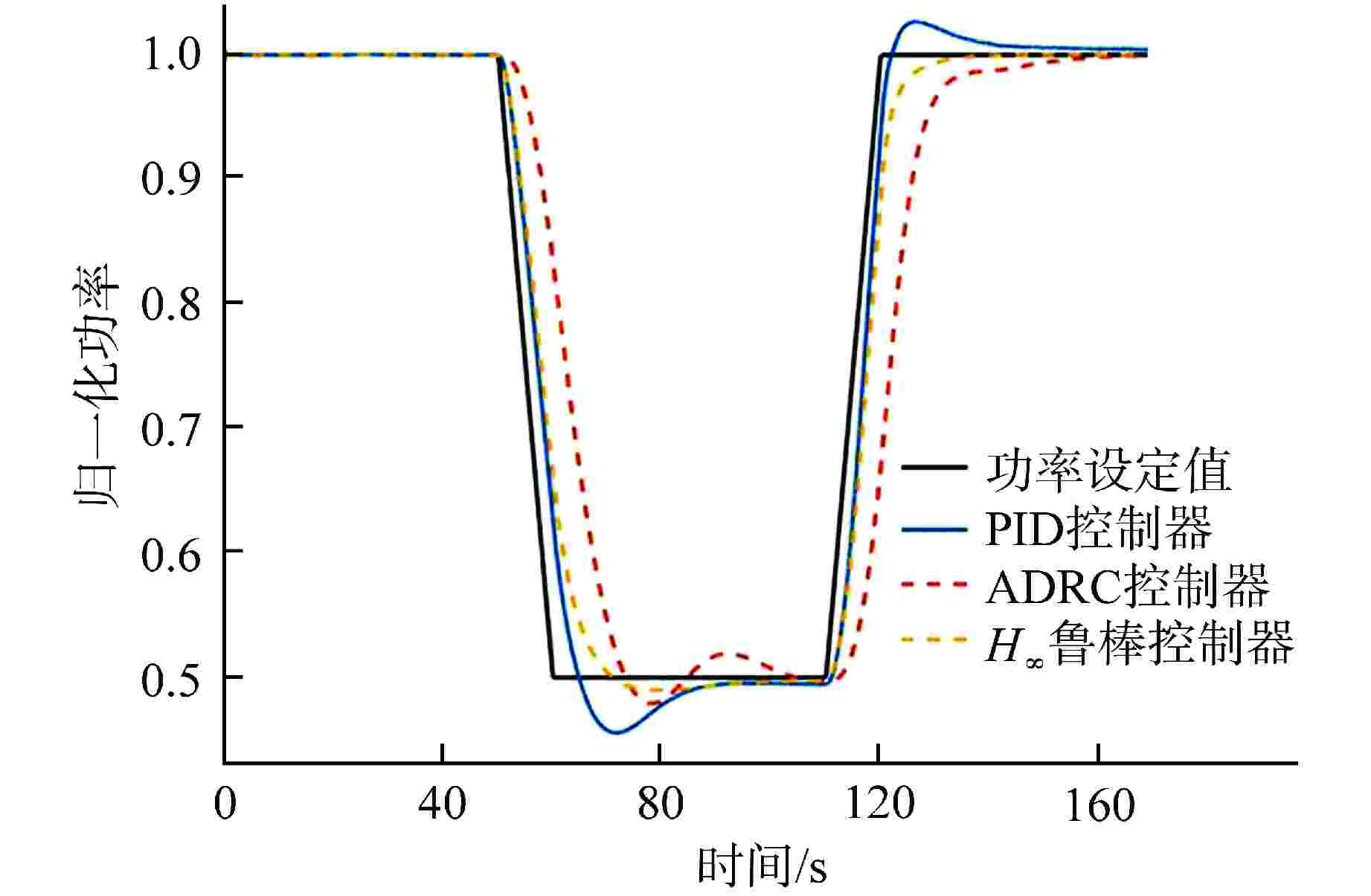
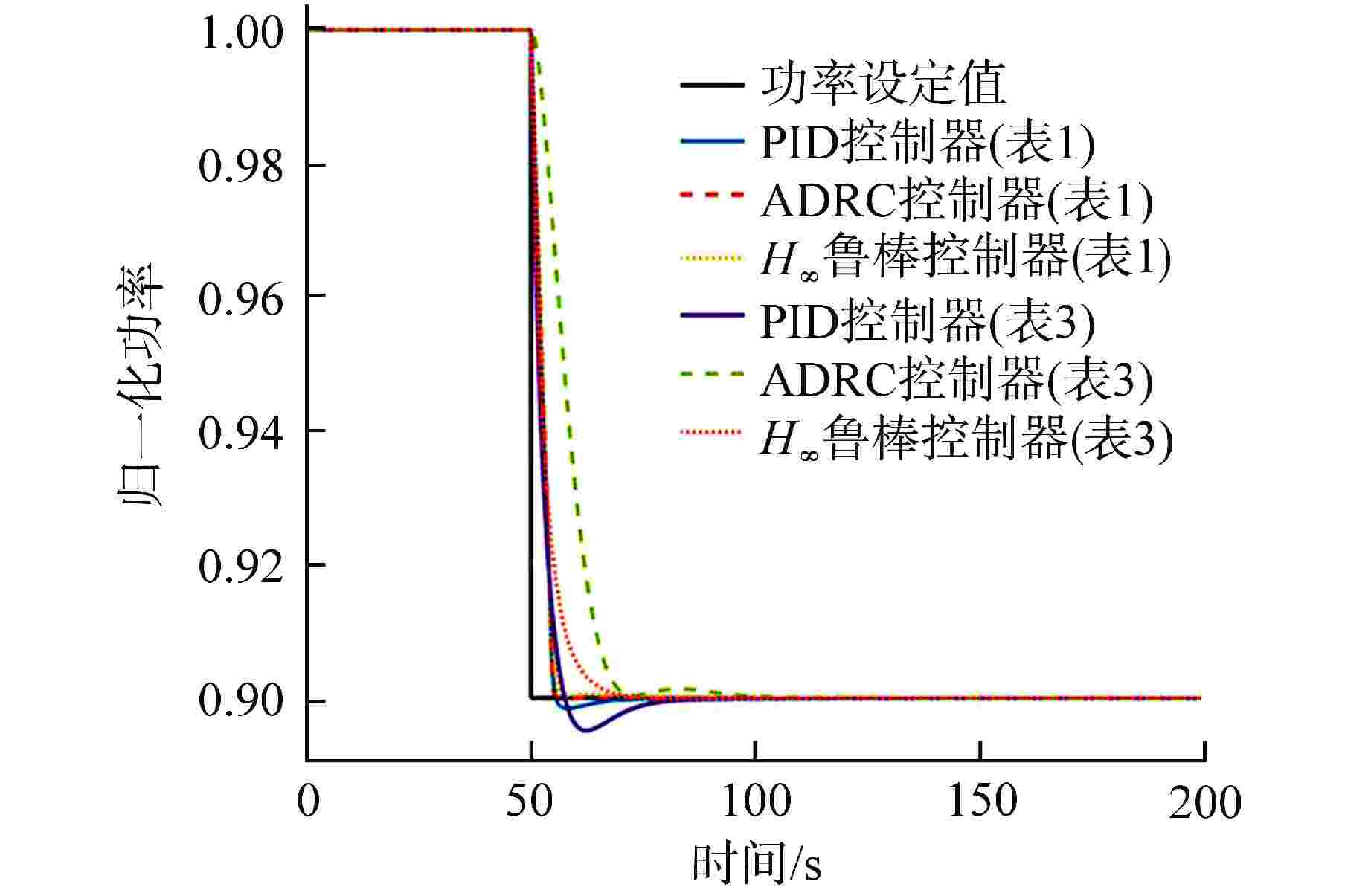
摘要: 铅铋冷却快堆多用于海洋、山区等偏远特殊环境的孤网供电，用户特性要求小型铅铋冷却快堆需具有良好的负荷跟踪能力。本文将3种不同的控制方法应用于铅铋冷却快堆堆芯功率控制，通过引入噪声、死区、时滞等环节对控制器的稳定性和设定值跟踪能力进行了测试。结果表明，比例-积分-微分（PID）控制器很难达到较好的控制效果，因此工业应用时往往加入了其他环节以保证PID控制器的稳定性。自抗扰（ADRC）控制器和H∞鲁棒控制器都具有良好的抗噪能力，能够独立地完成较好的控制效果，但良好的抗噪能力要牺牲一定的灵敏性。通过对3种控制器的比较分析表明，由于仿真计算对实际对象进行了简化，在这样的条件下所设计的控制器应选择较为保守的参数。
-
关键词:
- 铅铋冷却快堆 /
- 堆芯功率控制 /
- 比例-积分-微分（PID） /
- 自抗扰（ADRC）控制器 /
- H∞鲁棒控制器
Abstract: Lead-bismuth cooled fast reactors are mostly used for isolated power supply in remote and special environments such as oceans and mountains. The characteristics of users require that small lead-bismuth cooled fast reactors have good load following ability. In this paper, three different control methods are applied to the core power control of lead-bismuth cooled fast reactor, and the stability and set value tracking ability of the controller are tested by introducing noise, dead zone and time lag. The results show that the proportional integral derivative (PID) controller is difficult to achieve good control effect, so other links are often added in industrial applications to ensure the stability of the PID controller. Both active disturbance rejection control (ADRC) and H∞ robust controller have good anti-noise ability, and can independently achieve good control effect, but good anti-noise ability must sacrifice a certain sensitivity. The comparative analysis of the three kinds of controllers shows that because the simulation calculation simplifies the actual object, the controller designed under such conditions shall be designed with more conservative parameters. -
图 1 H∞鲁棒控制器一般结构
r—参考值；u—控制器输出/被控对象的输入；y—系统输出；e—误差；G(s)—被控对象的传递函数；K(s)—控制器的传递函数；W1(s)—灵敏度加权函数；W2(s) —控制量加权函数；W3(s)—补灵敏度加权函数；z1、z2、z3—系统的评价信号；s—拉普拉斯算子
Figure 1. General Structure of H∞ Robust Controller
图 2 小型铅铋冷却快堆仿真平台
模块1—设定值模块；模块2—死区模块；模块3—限幅模块；模块4—时滞模块；模块5—控制器切换模块；模块6—被控对象模块；模块7—测量噪声模块
Figure 2. Simulation Platform for Small Lead-Bismuth Cooled Fast Reactor
图 3 3种控制器仅在限幅约束下的归一化功率
Figure 3. Normalized Power for Three Controllers Only under Limiting Constraints
图 4 测量信号存在时滞时归一化功率
Figure 4. Normalized Power When the Measurement Signal Has a Time Lag
图 8 图2中模块全部打开时归一化功率
Figure 8. Normalized Power When All Modules in Figure 2 Are Turned On
表 1 第1次整定后控制器参数
Table 1. Controller Parameters After the First Tuning
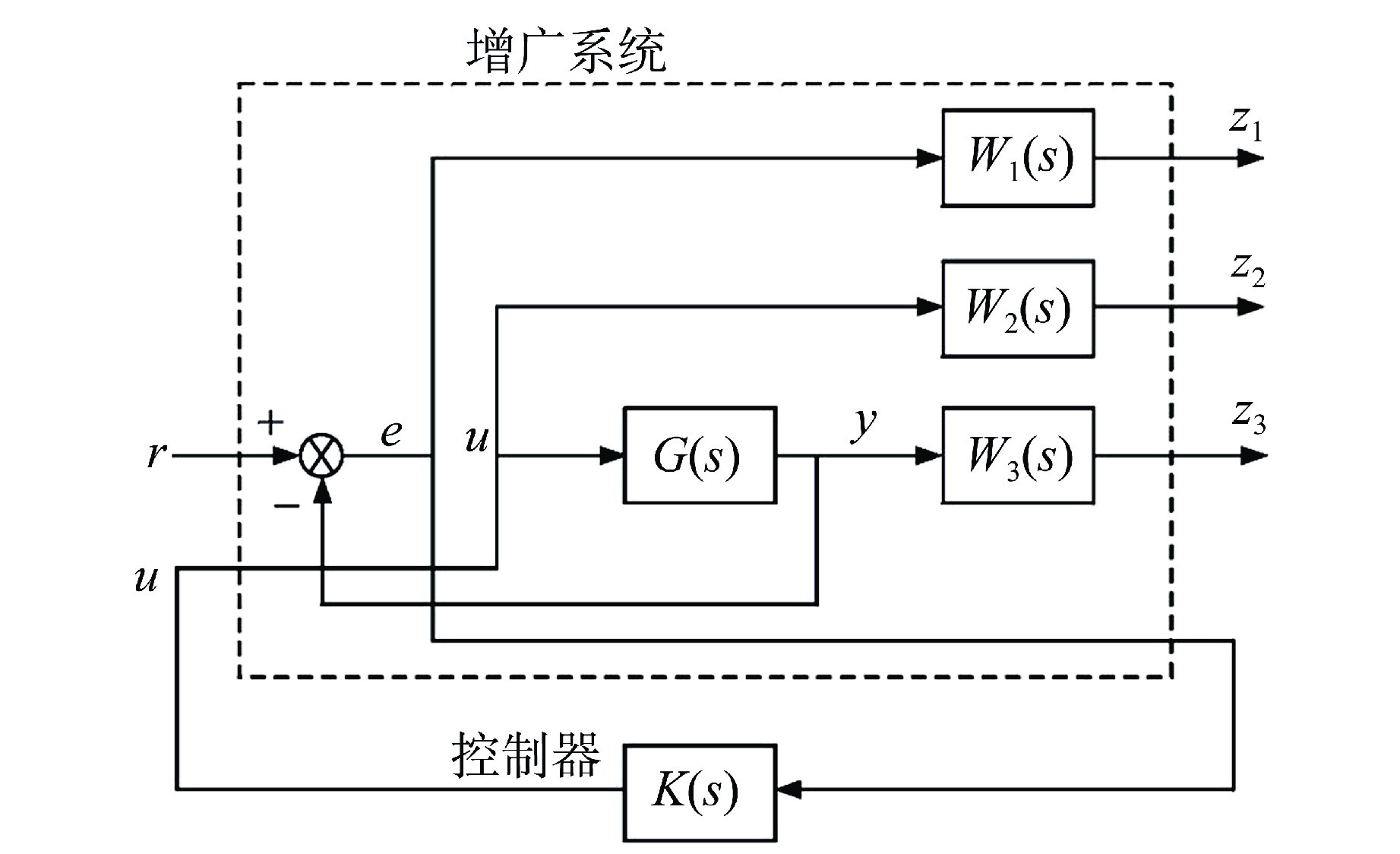
控制器 参数 数值 PID控制器 比例系数（kp） −1000 微分系数（kd） 0 ADRC控制器 控制量增益（b0） 854.6 ESO带宽（ω0） 1300 kp 5600 kd 13920 H∞鲁棒控制器 W1(s) ${6 \mathord{\left/ {\vphantom {6 {(9s + 0.9)}}} \right. } {(9s + 0.9)}}$ W2(s) 0.0001 W3(s) ${{60} \mathord{\left/ {\vphantom {{60} {(80s + 10)}}} \right. } {(80s + 10)}}$ 
下载: 导出CSV
表 2 第2次整定后控制器参数
Table 2. Controller Parameters After the Second Tuning
控制器 参数 数值 PID控制器 kp −100 kd 0 ADRC控制器 b0 854.6 ω0 300 kp 5600 kd 46080 H∞鲁棒控制器 W1(s) ${6 \mathord{\left/ {\vphantom {6 {(9s + 0.9)}}} \right. } {(9s + 0.9)}}$ W2(s) 0.0001 W3(s) ${{60} \mathord{\left/ {\vphantom {{60} {(80s + 10)}}} \right. } {(80s + 10)}}$
下载: 导出CSV
表 3 第3次整定后控制器参数
Table 3. Controller Parameters After the Third Tuning
控制器 参数 数值 PID控制器 kp −40 kd 0 ADRC控制器 b0 854.6 ω0 300 kp 5600 kd 46080 H∞鲁棒控制器 W1(s) ${6 \mathord{\left/ {\vphantom {6 {(3s + 0.9)}}} \right. } {(3s + 0.9)}}$ W2(s) 0.0001 W3(s) ${{120} \mathord{\left/ {\vphantom {{120} {(40s + 10)}}} \right. } {(40s + 10)}}$
下载: 导出CSV
-
[1] 李韡. 第四代核能系统技术开发及国际合作[J]. 国外核新闻,2003(6): 7-9. [2] LOCATELLI G, BINGHAM C, MANCINI M. Small modular reactors: a comprehensive overview of their economics and strategic aspects[J]. Progress in Nuclear Energy, 2014, 73: 75-85. [3] 韩金盛,刘滨,李文强. 铅冷快堆研究概述[J]. 核科学与技术,2018, 6(3): 87-97. [4] 王春阳,马帅,梁书宁,等. 光电稳瞄平台基于自抗扰的改进内模控制[J]. 电光与控制,2021, 28(2): 78-82. [5] 侯忠生,许建新. 数据驱动控制理论及方法的回顾和展望[J]. 自动化学报,2009, 35(6): 650-667. [6] 韩京清. 从PID技术到“自抗扰控制”技术[J]. 控制工程,2002, 9(3): 13-18. doi: 10.3969/j.issn.1671-7848.2002.03.003 [7] AMATO F, PIRONTI A. H∞optimal terminal state control for linear systems with lumped and distributed time delays[J]. Automatica, 1999, 35(9): 1619-1624. doi: 10.1016/S0005-1098(99)00063-1 [8] SUZUKI K, SHIMAZAKI J, SHINOHARA Y. Application of H∞ control theory to power control of a nonlinear reactor model[J]. Nuclear Science and Engineering, 1993, 115(2): 142-151. doi: 10.13182/NSE92-112 [9] CHI S G, CHO N Z. H∞ control theory applied to xenon control for load-following operation of a nuclear reactor[J]. Nuclear Technology, 2002, 137(2): 127-138. doi: 10.13182/NT00-31 [10] 闫旭. 小型压水堆H∞鲁棒控制研究[D]. 西安: 西安交通大学, 2019: 24-27. [11] SUN A D, PU S M, HE Z X, et al. Application of model free active disturbance rejection controller in nuclear reactor power control[J]. Progress in Nuclear Energy, 2021, 140: 103907. doi: 10.1016/j.pnucene.2021.103907 -
计量
- 文章访问数: 193
- HTML全文浏览量: 56
- PDF下载量: 62
- 被引次数: 0
