Study on Creep Model of Pre-stressed Concrete Based on Component Scale
-
摘要: 为评估核电厂安全壳结构的长期预应力损失，以预应力混凝土梁为研究对象，采用试验研究与理论分析相结合的方法，建立预应力混凝土徐变预测模型。在已有的预应力混凝土梁徐变试验基础上，采用相同的混凝土材料进行相同环境下的收缩试验，以测定预应力混凝土梁的实际收缩变形。考虑到混凝土收缩、徐变、预应力筋松弛的耦合作用，引入龄期调整有效模量法，建立由试验数据推导混凝土徐变系数的计算方法，最终建立预应力混凝土徐变模型并预测其长期徐变变形，为核电厂安全壳结构长期预应力损失评估提供了理论支撑。Abstract: To assess long-term pre-stress loss of nuclear power plant containment, the creep prediction model of pre-stressed concrete is established by combining experimental investigation with theoretical analysis by taking pre-stressed concrete beam as the research object. Based on the existing creep test of pre-stressed concrete beams, the shrinkage test of pre-stressed concrete beams under the same environment is carried out with the same concrete materials to measure the actual shrinkage deformation of pre-stressed concrete beams. Considering the coupling effect of concrete shrinkage, creep and pre-stressed tendon relaxation, the age adjusted effective modulus method is introduced to establish the calculation method of concrete creep coefficient derived from the test data. Finally, the creep model of pre-stressed concrete is established and its long-term creep deformation is predicted, which provides a theoretical support for the long-term pre-stress loss assessment of nuclear power plant containment structure.
-
Key words:
- Containment /
- Concrete /
- Pre-stress /
- Creep /
- Shrinkage
-
图 1 预应力混凝土梁概况 (单位：mm)
@100表示箍筋间距
Figure 1. General Situation of Pre-Stressed Concrete Beam (Unit: mm)
图 2 根据收缩试验得到的小、大尺寸试件收缩应变
Figure 2. Shrinkage Strain of Small- and Large-Size Specimens According to Shrinkage Test
图 3 试件体表比与预应力混凝土T型梁干燥收缩应变
Figure 3. Ratio of Specimen Volume to Surface Area and Drying Shrinkage Strain of Pre-Stresses T-shaped Beam
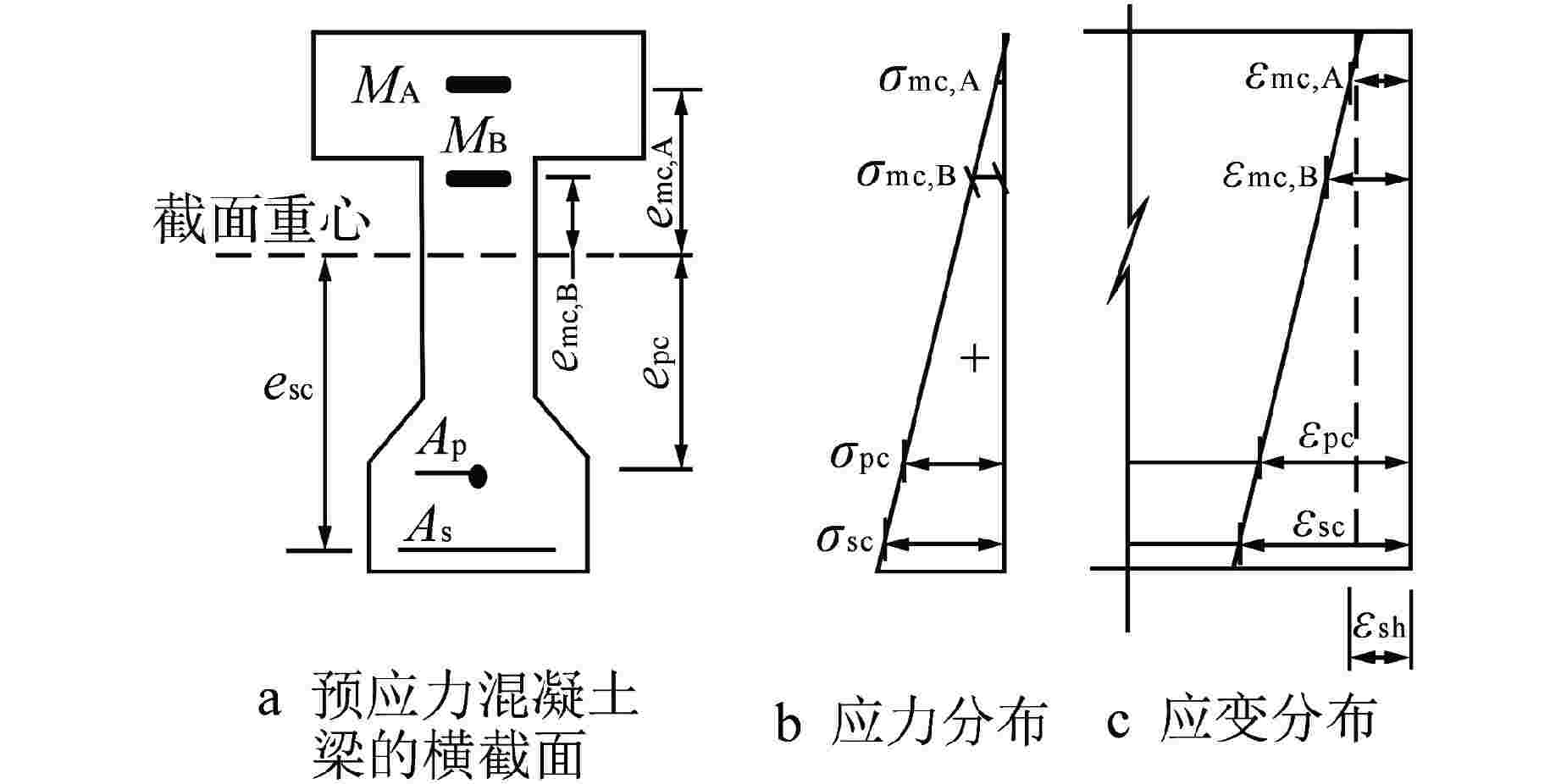
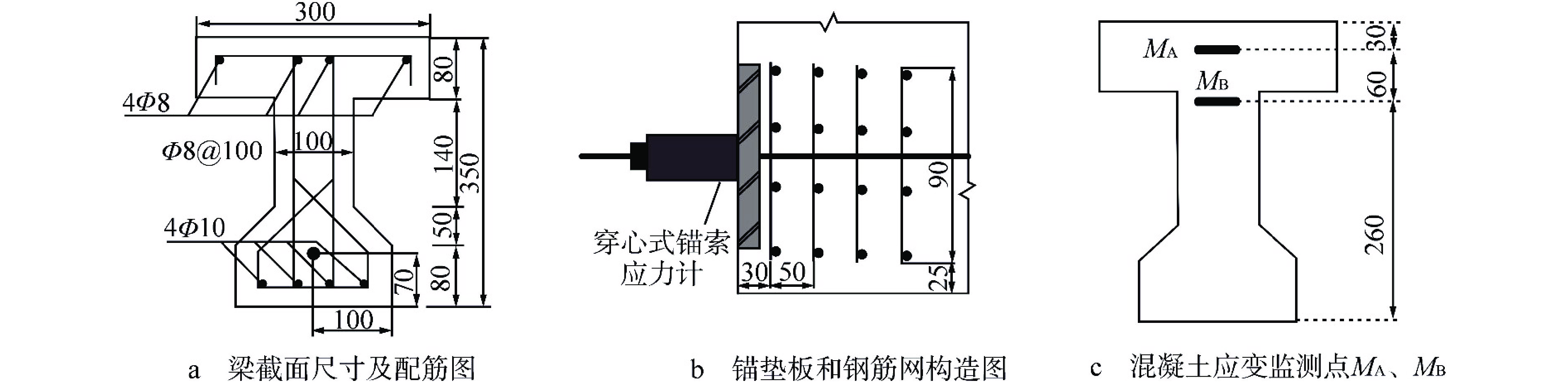
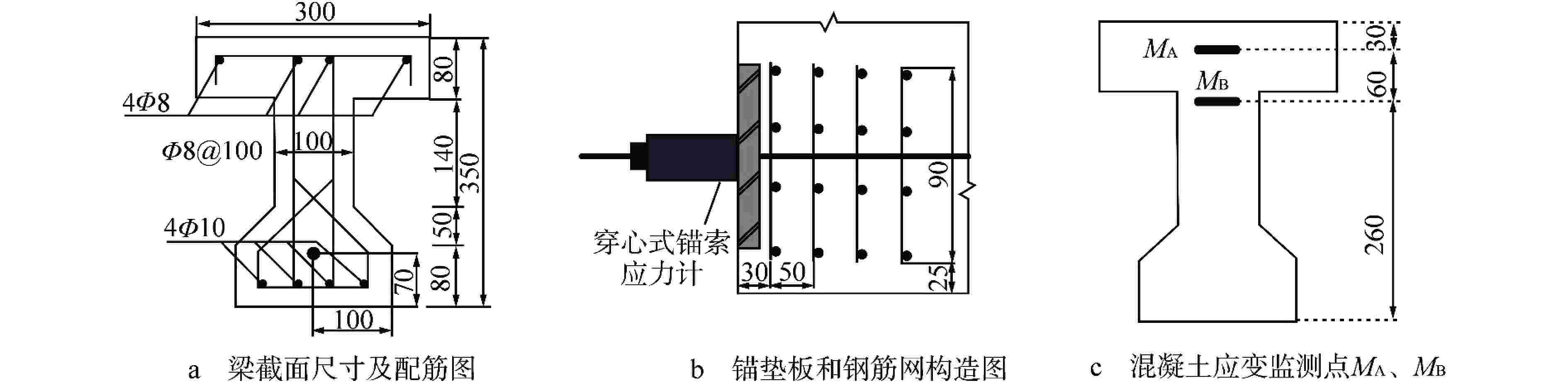
图 4 预应力混凝土梁截面应力应变分布
Ap、As—预应力筋和普通钢筋截面面积；epc、esc—预应力筋、普通钢筋重心至截面重心的距离；emc,A、emc,B—测点M A、M B至截面重心的距离；εsc、εpc、εmc,A、εmc,B—预应力筋重心处、普通钢筋重心处、测点A处、测点B处混凝土的应变；εsh—混凝土收缩应变；σsc、σpc、σmc,A、σmc,B—预应力筋重心处、普通钢筋重心处、测点MA处、测点MB处混凝土的应力。
Figure 4. Stress and Strain Distributions at Cross Section of Pre-stress Concrete Beam
图 5 根据试验结果计算的混凝土梁$\varphi (t,{t_0})$
Figure 5. Concrete Beam φ(t,t0) Calculated from Test Results
图 6 试验结果与规范推荐的$\varphi (t,{t_0})$对比
Figure 6. Comparison of the Test Results with the φ(t,t0) Recommended by the Specification
图 7 梁L1中测点MA、MB处的混凝土应变
Figure 7. Concrete Strain at Measuring Points MA and MB in Beam L1
图 8 预应力混凝土梁L5测点MA、MB处10 a周期应变预测
Figure 8. Prediction of 10 a Cyclic Strain at Measuring Points MA and MB of Pre-stressed Concrete Beam L5
图 9 预应力混凝土梁L5测点MA、MB处长期应变增长率
Figure 9. Long-term Strain Growth Rate at Measuring Points MA and MB of Pre-stressed Concrete Beam L5
表 1 混凝土配合比 kg/m3
Table 1. Mix Proportion of Concrete kg/m3
成份 水泥 水 砂子 石子 粉煤灰 矿渣 外加剂 含量 420 175 692 1030 60 20 14.8 
下载: 导出CSV
表 2 预应力混凝土梁L1~L6加载方案
Table 2. Loading Scheme for Pre-Stressed Concrete Beams L1~L6
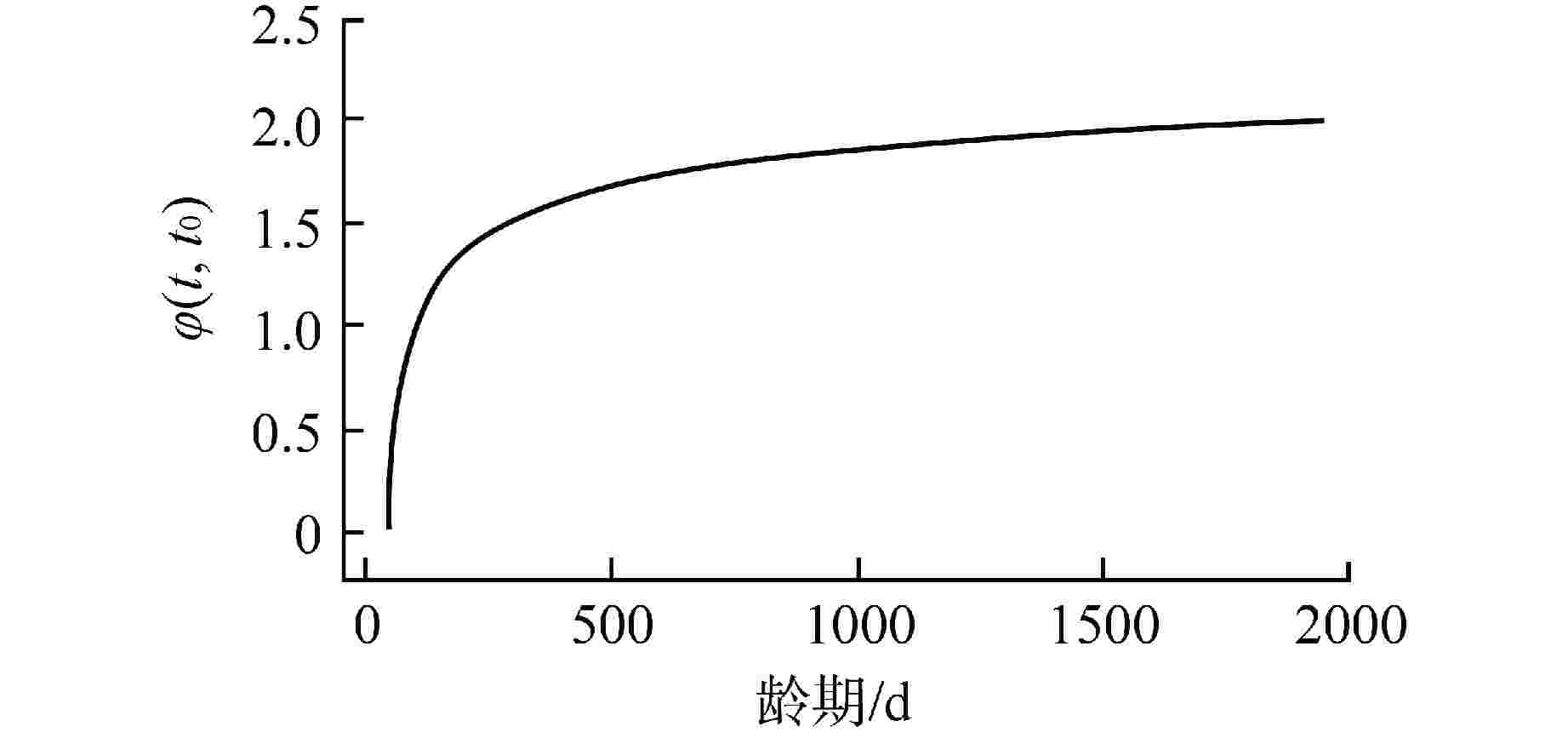
梁编号 L1 L2 L3 L4 L5 L6 预应力张拉龄期/d 23 23 23 45 45 45 张拉控制应力/MPa 0.65fpk 0.60 fpk 0.65 fpk 0.70 fpk 0.75 fpk 0.73 fpk 锚固后实际预应力/kN 141 135 147 153 175 165 外荷载施加龄期/d 180 180 180 180 180 180 外荷载水平/kN 52.0 48.0 52.0 51.0 60.0 53.0
下载: 导出CSV
表 3 $\varphi (t,{t_0})$中待定参数的对比
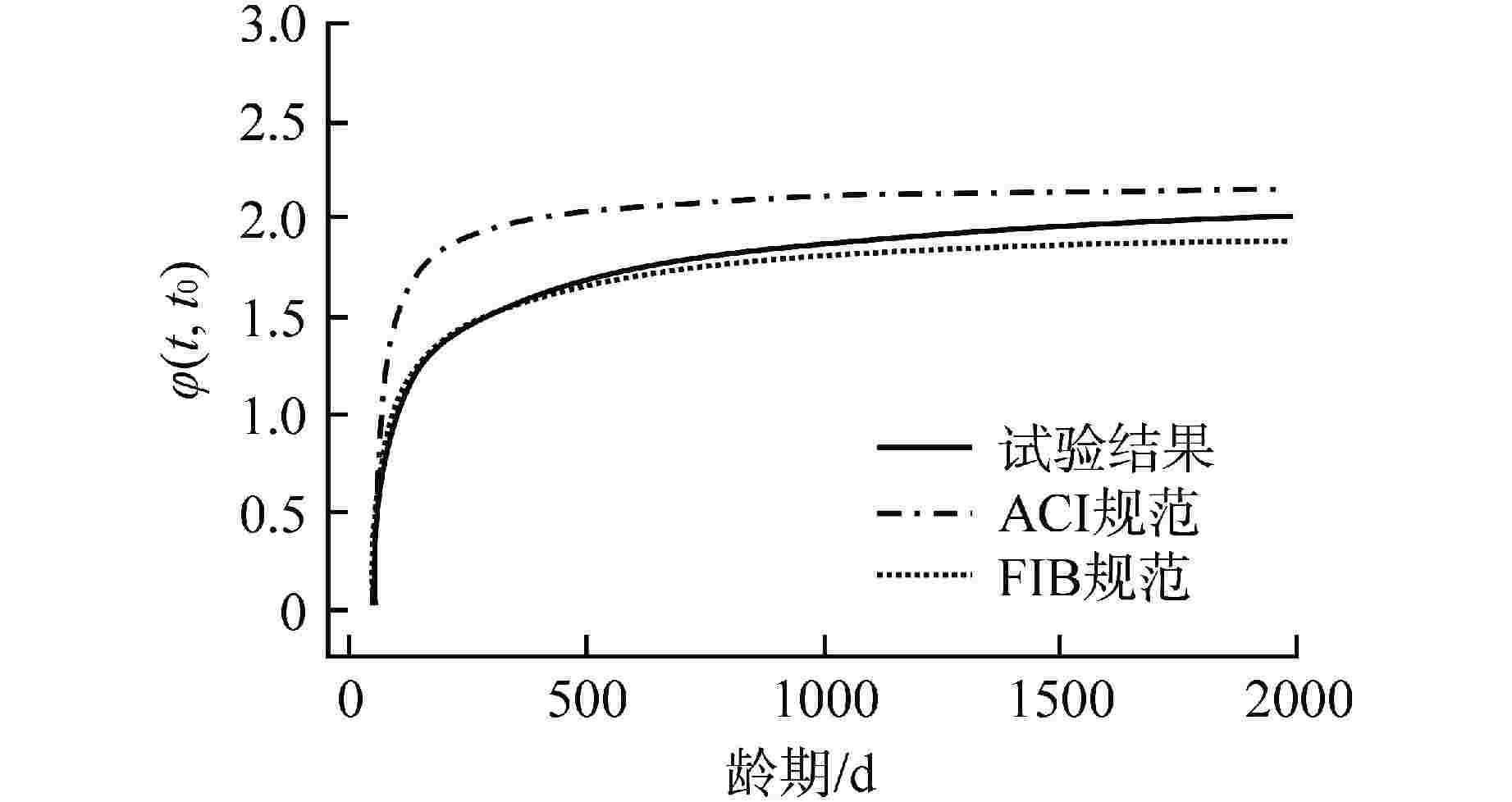
Table 3. Comparison of Undetermined Parameters in φ(t,t0)
所用规范 a b c ACI规范 0.60 10.00 −0.070 试验修正 (ACI) 0.57 13.19 −0.072 FIB规范 0.35 0.88 — 试验修正 (FIB) 0.39 1.19 — “—”表示该模型无相关参数
下载: 导出CSV
-
[1] 王晓磊,侯钢领,吕大刚. 某核电站安全壳1∶15模型振动台试验[J]. 工程力学,2014, 31(S1): 249-252,264. [2] 吴锋,卓杨,曹进捷,等. 后张法预应力混凝土管桩长期预应力损失研究[J]. 混凝土与水泥制品,2009(2): 36-37. [3] 汪建群,吕鹏,许巧,等. 混凝土徐变计算模型及其实用性评述[J]. 工程力学,2018, 35(S1): 156-160. [4] 寒秋. 混凝土收缩徐变的粘弹性随机性算法研究[D]. 北京: 北京交通大学, 2019. [5] BAŽANT Z P, BAWEJA S. Creep and shrinkage prediction model for analysis and design of concrete structures: model B3[J]. Materials and Structures, 1995, 28(6): 357-365. doi: 10.1007/BF02473152 [6] WENDNER R, HUBLER M H, BAŽANT Z P. Statistical justification of model B4 for multi-decade concrete creep using laboratory and bridge databases and comparisons to other models[J]. Materials and Structures, 2015, 48(4): 815-833. doi: 10.1617/s11527-014-0486-1 [7] YANG M F, JIN S, GONG J X. Concrete creep analysis method based on a long-term test of prestressed concrete beam[J]. Advances in Civil Engineering, 2020, 2020: 3825403. [8] 王勋文,潘家英. 按龄期调整有效模量法中老化系数x的取值问题[J]. 中国铁道科学,1996, 17(3): 12-23. [9] 胡狄. 预应力混凝土桥梁徐变效应分析[D]. 长沙: 中南大学, 2003. [10] 高永亮. 预应力混凝土构件长期应力损失计算[D]. 长沙: 中南大学, 2014. -
计量
- 文章访问数: 49
- HTML全文浏览量: 12
- PDF下载量: 12
- 被引次数: 0
