Research on Nonlinearity Weakening Method of Quasi-zero-stiffness Vibration Isolator
-
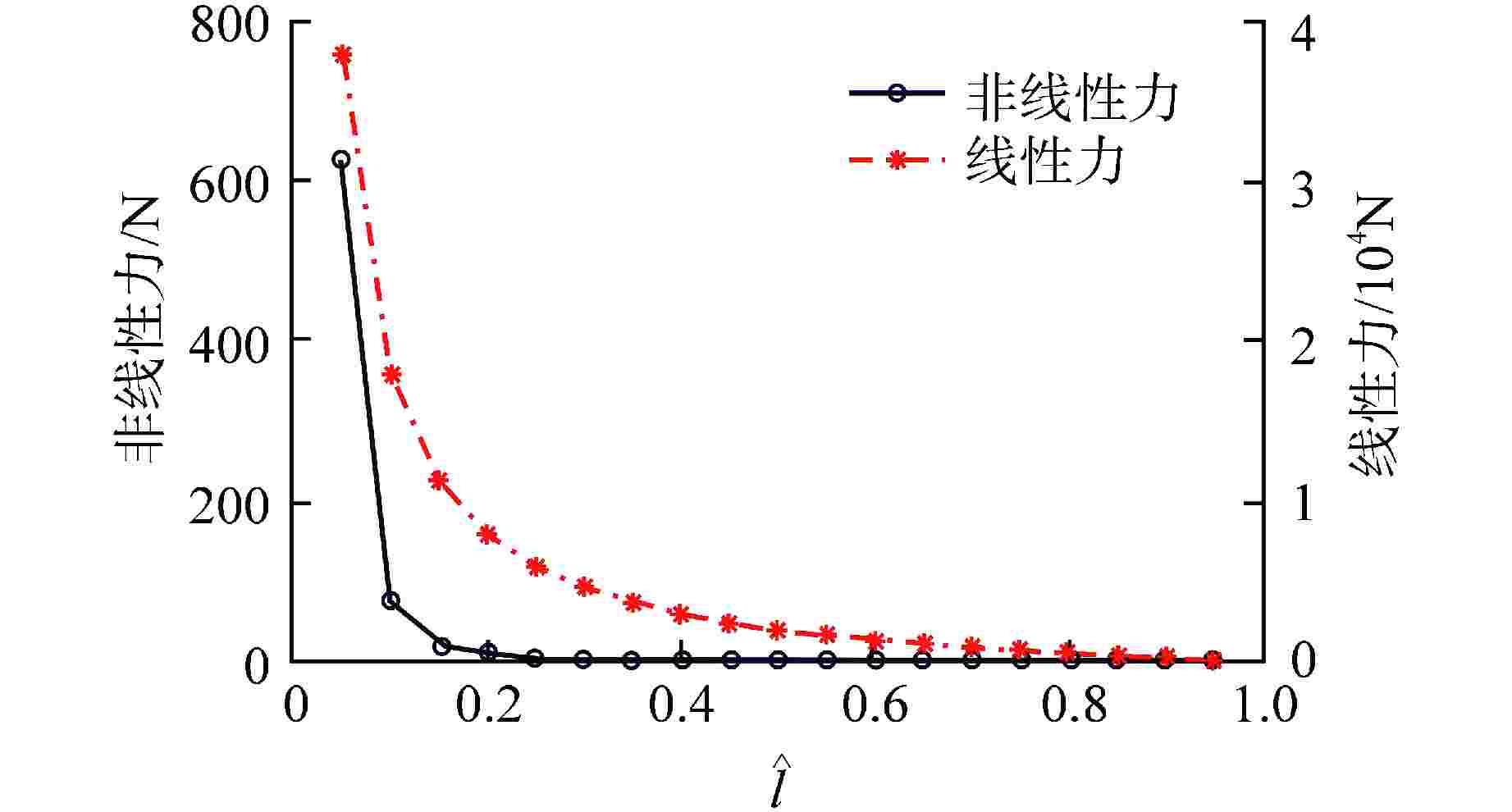
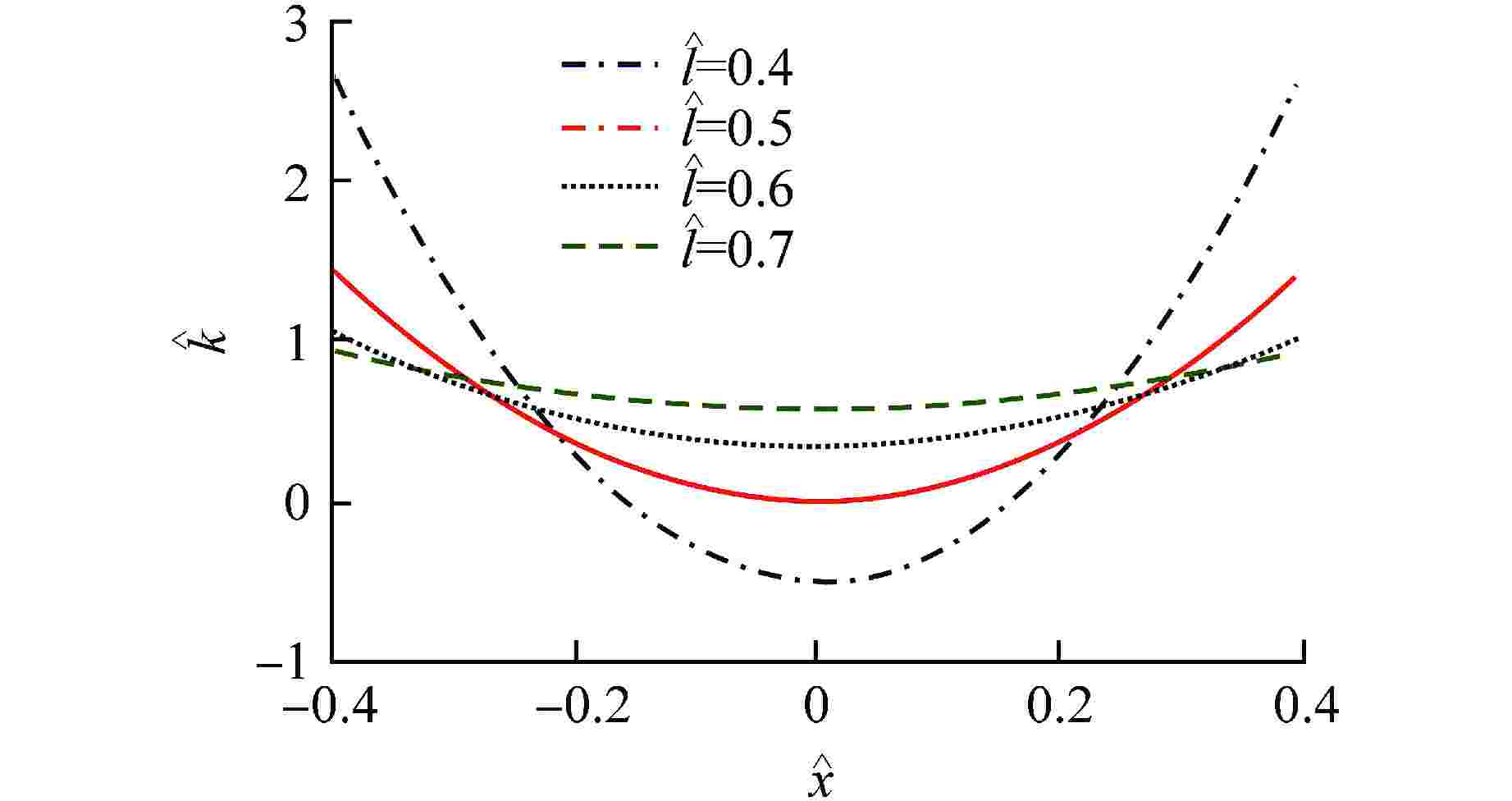
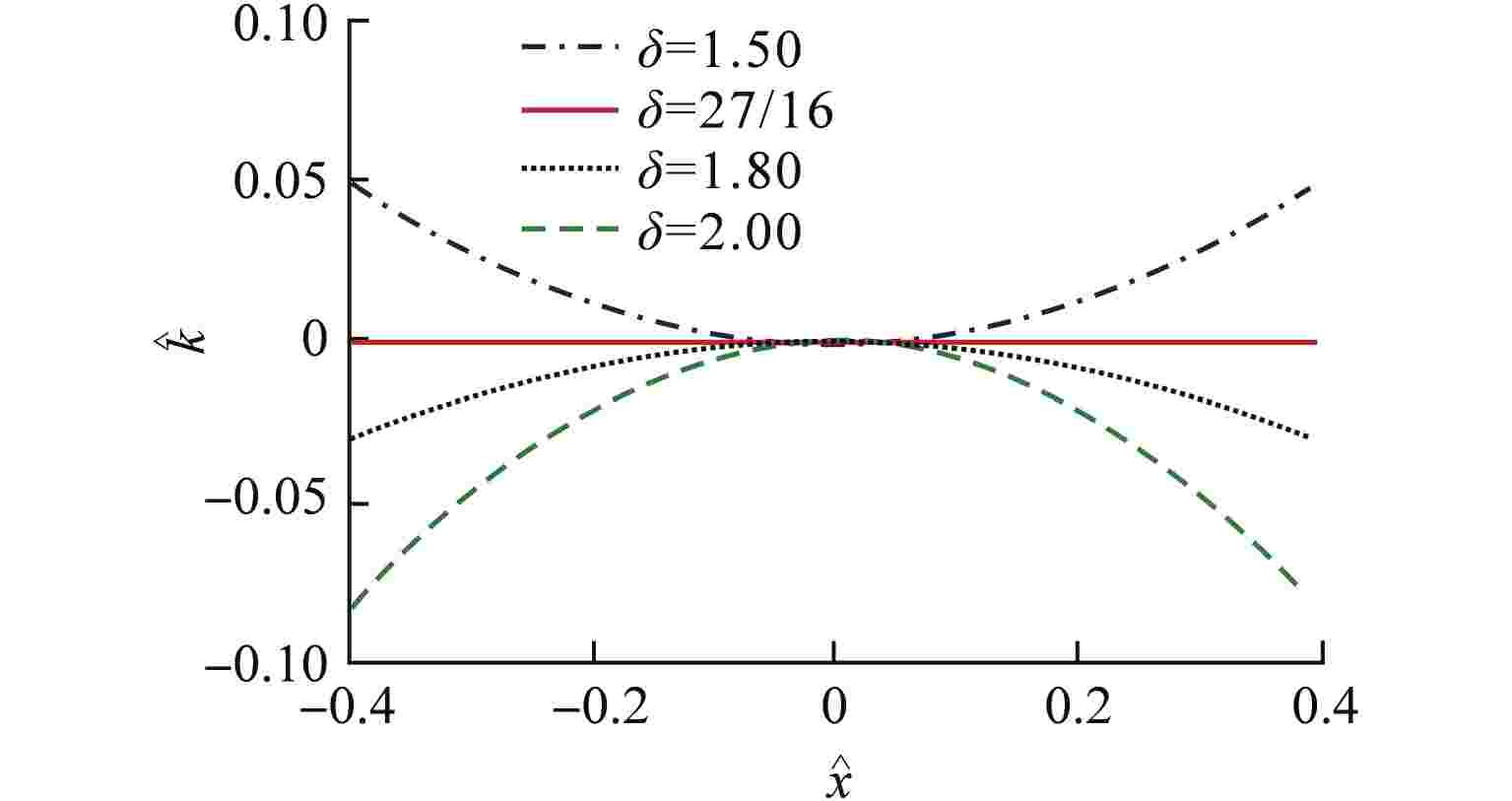
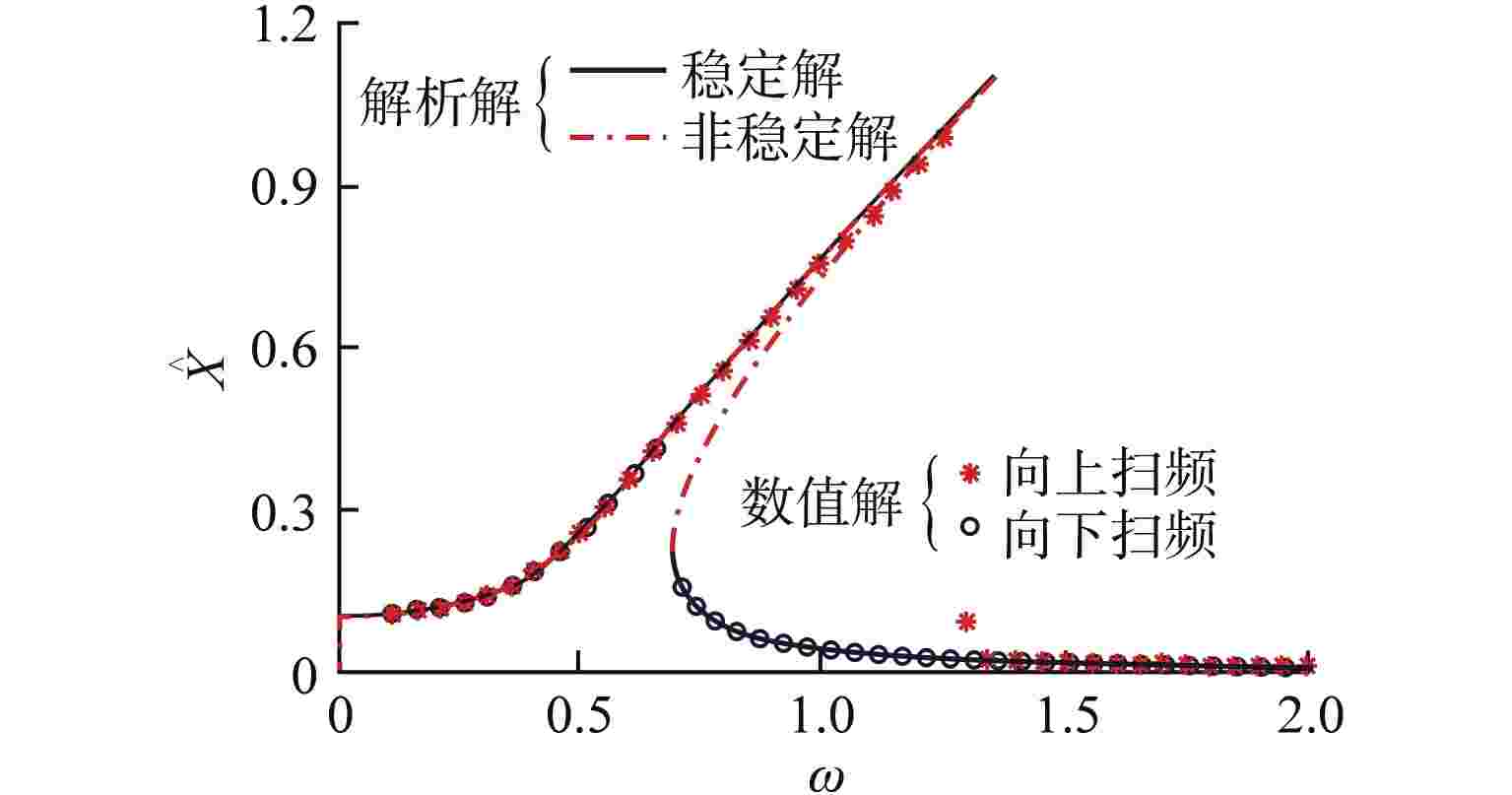
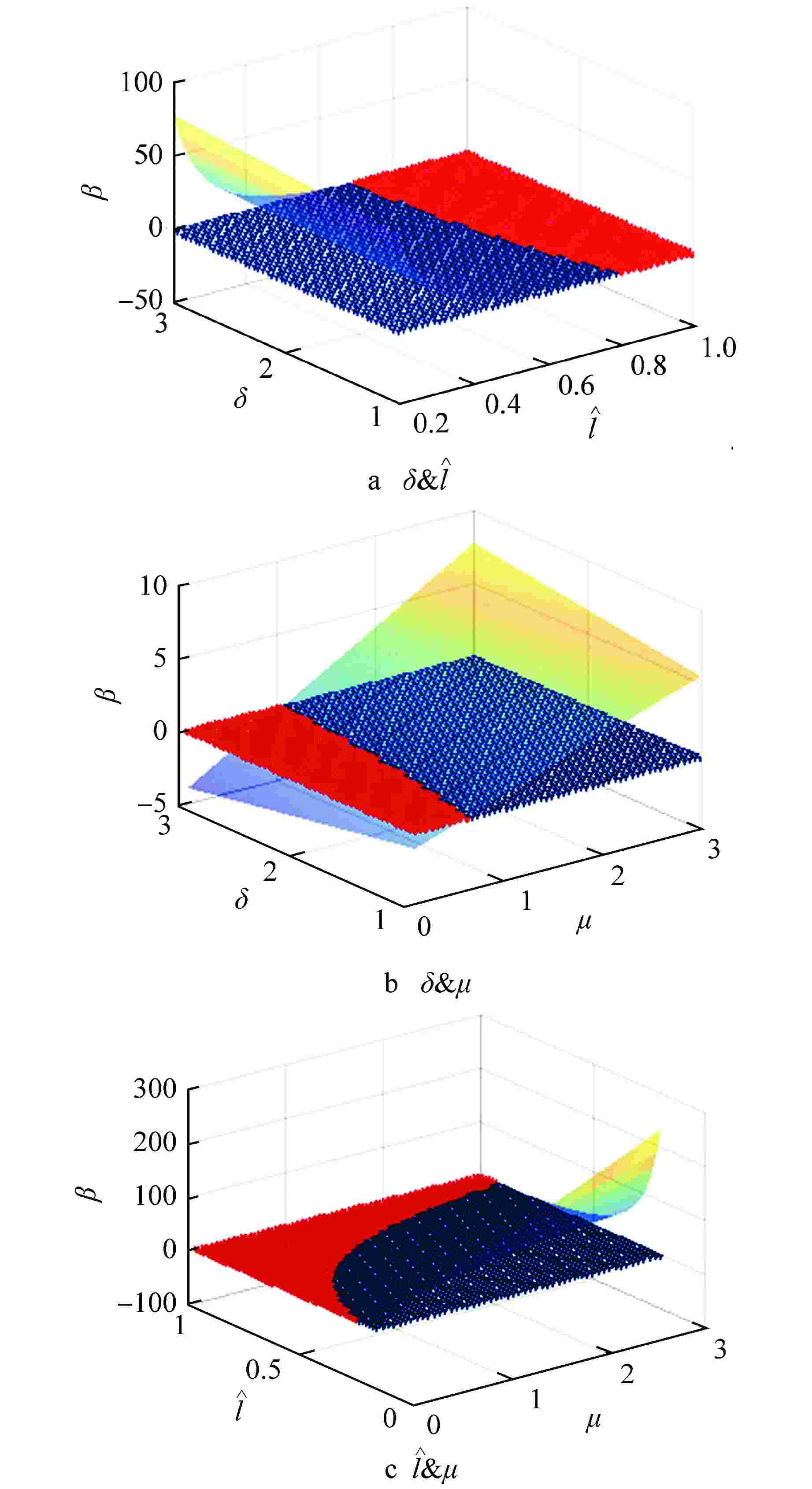
摘要: 为削弱准零刚度隔振器的非线性特性，提出一种利用渐软负刚度中和渐硬负刚度的准零刚度隔振器非线性削弱方法，通过调整设计参数，使得2种负刚度的非线性项相互抵消，系统仅保留线性刚度特性。通过永磁体式负刚度及三弹簧式负刚度案例对该方法可行性进行验证。研究结果表明，利用该方法所设计的准零刚度隔振系统的非线性刚度得到极大削弱，系统隔振性能得到增强。Abstract: In order to weaken the nonlinear characteristics of the quasi-zero-stiffness vibration isolator, a nonlinearity weakening method of quasi-zero-stiffness vibration isolator using softening negative stiffness to neutralize hardening negative stiffness is proposed. By adjusting the design parameters, the nonlinear terms of the two negative stiffness cancel each other out, and the system only retains the linear stiffness characteristics. The feasibility of this method is verified by the cases of permanent magnet negative stiffness and three-spring negative stiffness. The results show that the nonlinear stiffness of the quasi-zero-stiffness vibration isolation system designed by this method is greatly weakened and the vibration isolation performance of the system is enhanced.
-
Key words:
- Quasi-zero-stiffness (QZS) /
- Vibration isolation /
- Nonlinearity /
- Weakening method
-
图 1 准零刚度隔振器示意图
kv1—垂向弹簧I刚度；kv2—垂向弹簧II刚度；ko—横向弹簧刚度；l—横向弹簧水平长度；lo—横向弹簧原长；xs—无隔振质量时系统位置；x—系统位移；d—磁铁间距；m—隔振质量
Figure 1. Schematic Diagram of Quasi-zero-stiffness Vibration Isolator
图 3 不同$ \hat l $下隔振系统的刚度特性的变化曲线
Figure 3. Variation Curve of Stiffness Characteristics of Vibration Isolation System under Different Parameter $ \hat l $
图 4 不同参数δ下隔振系统的刚度特性变化曲线
Figure 4. Variation Curve of Stiffness Characteristics of Vibration Isolation System under Different Parameter δ
图 5 不同隔振系统下|Rnl|值随无量纲位移的变化曲线
Figure 5. Variation Curve of |Rnl| Value with Dimensionless Displacement under Different Vibration Isolation Systems
图 6 解析解与数值解的对比
Figure 6. Comparison between Analytical Solution and Numerical Solution
图 7 不同激励幅值下隔振系统的动力学特性
Figure 7. Dynamic Characteristics of Vibration Isolation System under Different Excitation Amplitudes
图 8 系统参数对于非线性刚度系数的影响
Figure 8. Effects of System Parameters on Nonlinear Stiffness Coefficient
图 9 系统参数对于EQZS-VI力传递率的影响
Figure 9. Effect of System Parameters on Force Transmissibility of EQZS-VI
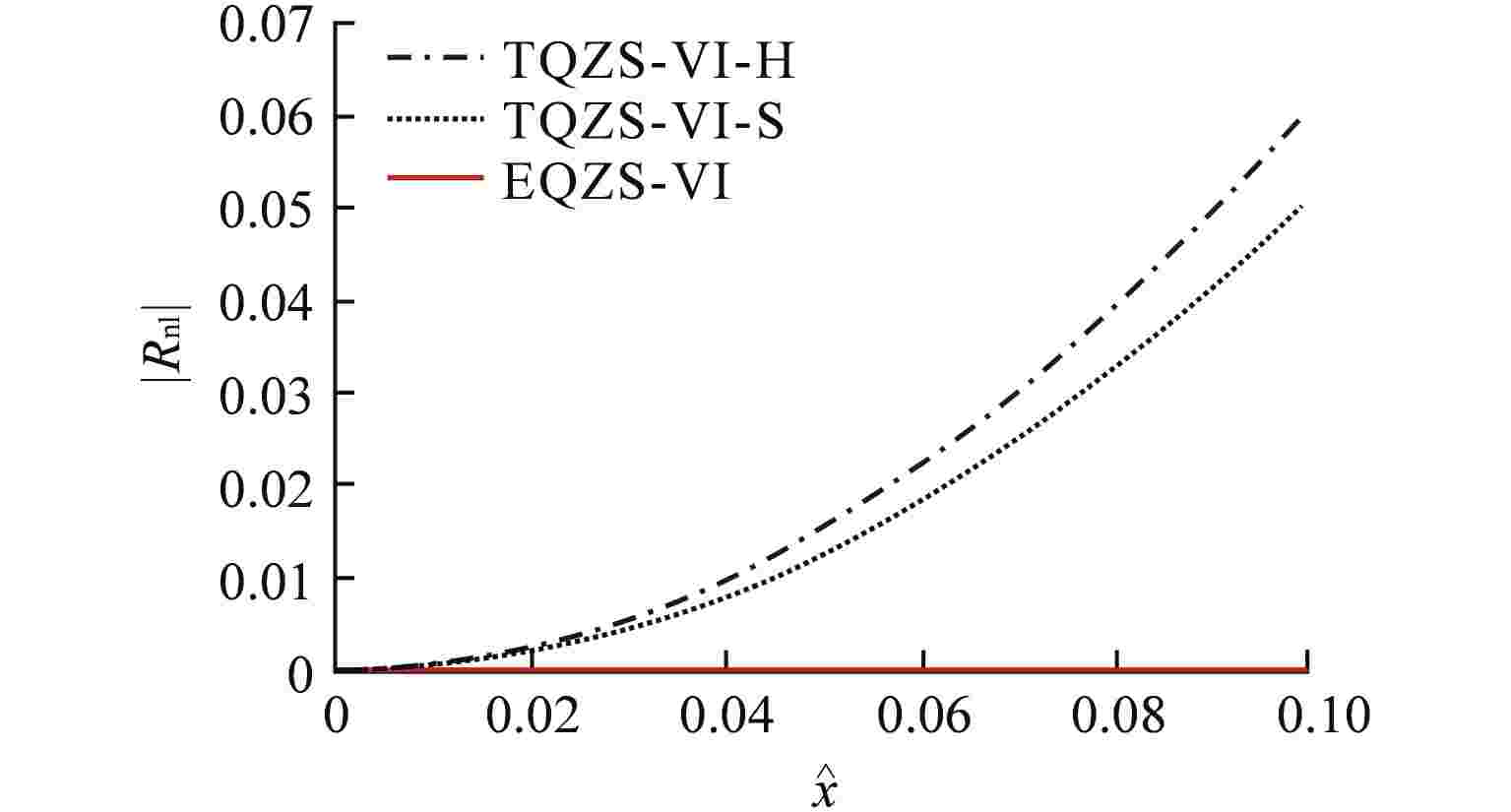
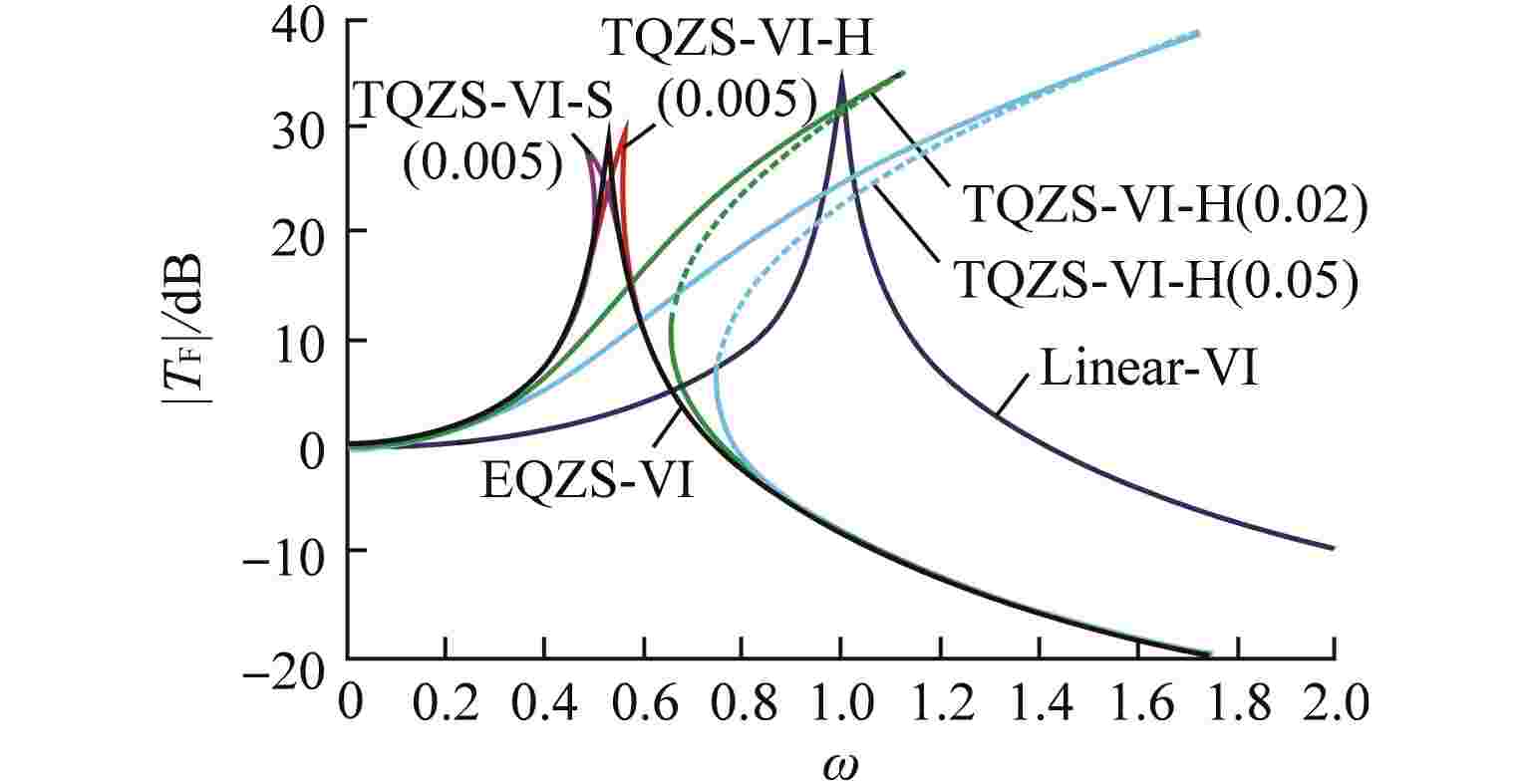
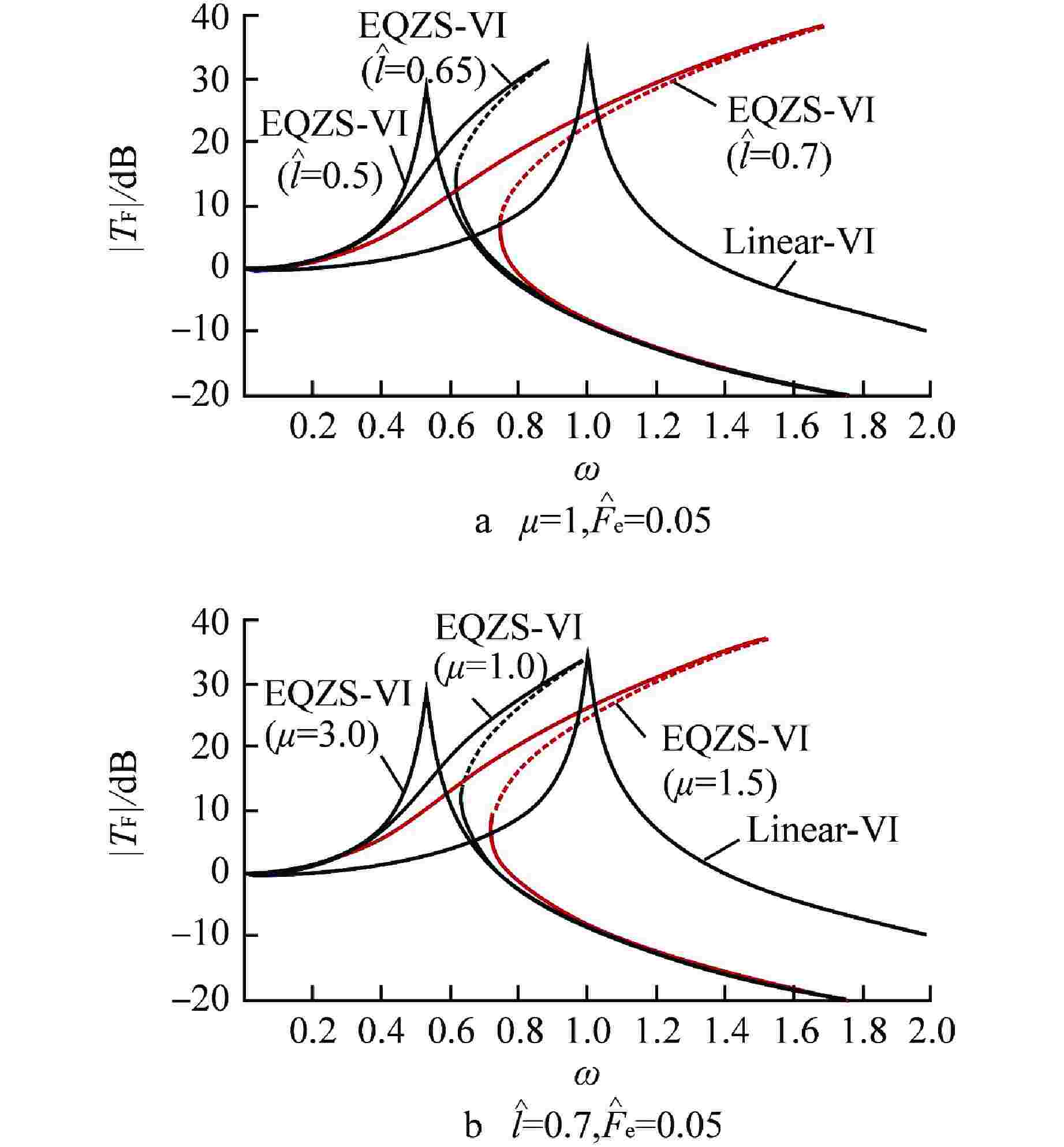
表 1 系统参数取值
Table 1. System Parameter Value
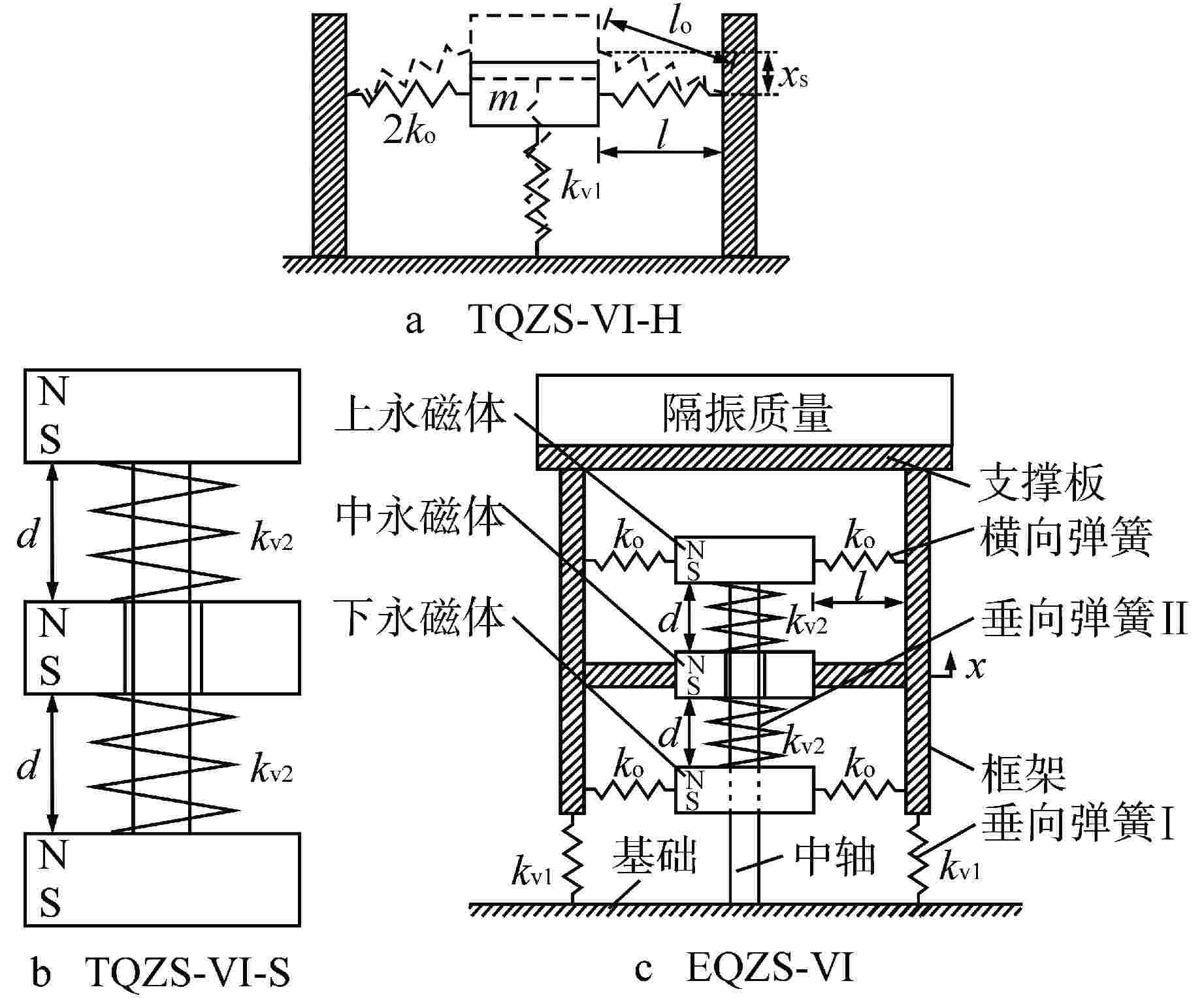
隔振器类型 参数 μ λ δ $ \hat l $ α β TQZS-VI-H 1 0 — 0.58 0.28 1.70 TQZS-VI-S 0 0.72 1.96 0.70 0.28 −1.44 EQZS-VI 1 0.33 2.50 0.70 0.28 0 “—”表示不涉及该参数 
下载: 导出CSV
-
[1] 刘天彦,李朋洲,张鲲,等. 管道系统金属橡胶支吊架性能实验研究[J]. 核动力工程,2019, 40(S1): 129-132. [2] 徐庆善. 隔振技术的进展与动态[J]. 机械强度,1994, 16(1): 37-42. [3] 张鲲,席文兵,李朋洲,等. 叶片泵线谱振动有源控制[J]. 核动力工程,2016, 37(S2): 99-102. [4] CARRELLA A, BRENNAN M J, WATERS T P, et al. On the design of a high-static–low-dynamic stiffness isolator using linear mechanical springs and magnets[J]. Journal of Sound and Vibration, 2008, 315(3): 712-720. doi: 10.1016/j.jsv.2008.01.046 [5] TANG B, BRENNAN M J. On the shock performance of a nonlinear vibration isolator with high-static-low-dynamic-stiffness[J]. International Journal of Mechanical Sciences, 2014, 81: 207-214. doi: 10.1016/j.ijmecsci.2014.02.019 [6] ZHOU N, LIU K. A tunable high-static–low-dynamic stiffness vibration isolator[J]. Journal of Sound and Vibration, 2010, 329(9): 1254-1273. doi: 10.1016/j.jsv.2009.11.001 [7] 闫振华,黄玉强,李学飞,等. 基于球面滚子机构的车辆座椅非线性悬架设计[J]. 吉林大学学报:工学版,2016, 46(3): 706-710. [8] 刘学广, 韩超, 范朝阳, 等. 一种具有线性负刚度特性的电磁弹簧: 中国, 201610147176.9[P]. 2018-05-18. [9] HAYASHI C. Nonlinear oscillations in physical systems[M]. New York: McGraw-Hill, 1964, 13-22. [10] NAYFEH A H, MOOK P D T. Nonlinear oscillations[M]. New York: John Wiley & Sons, 1979, 56-99. -
计量
- 文章访问数: 38
- HTML全文浏览量: 18
- PDF下载量: 4
- 被引次数: 0
