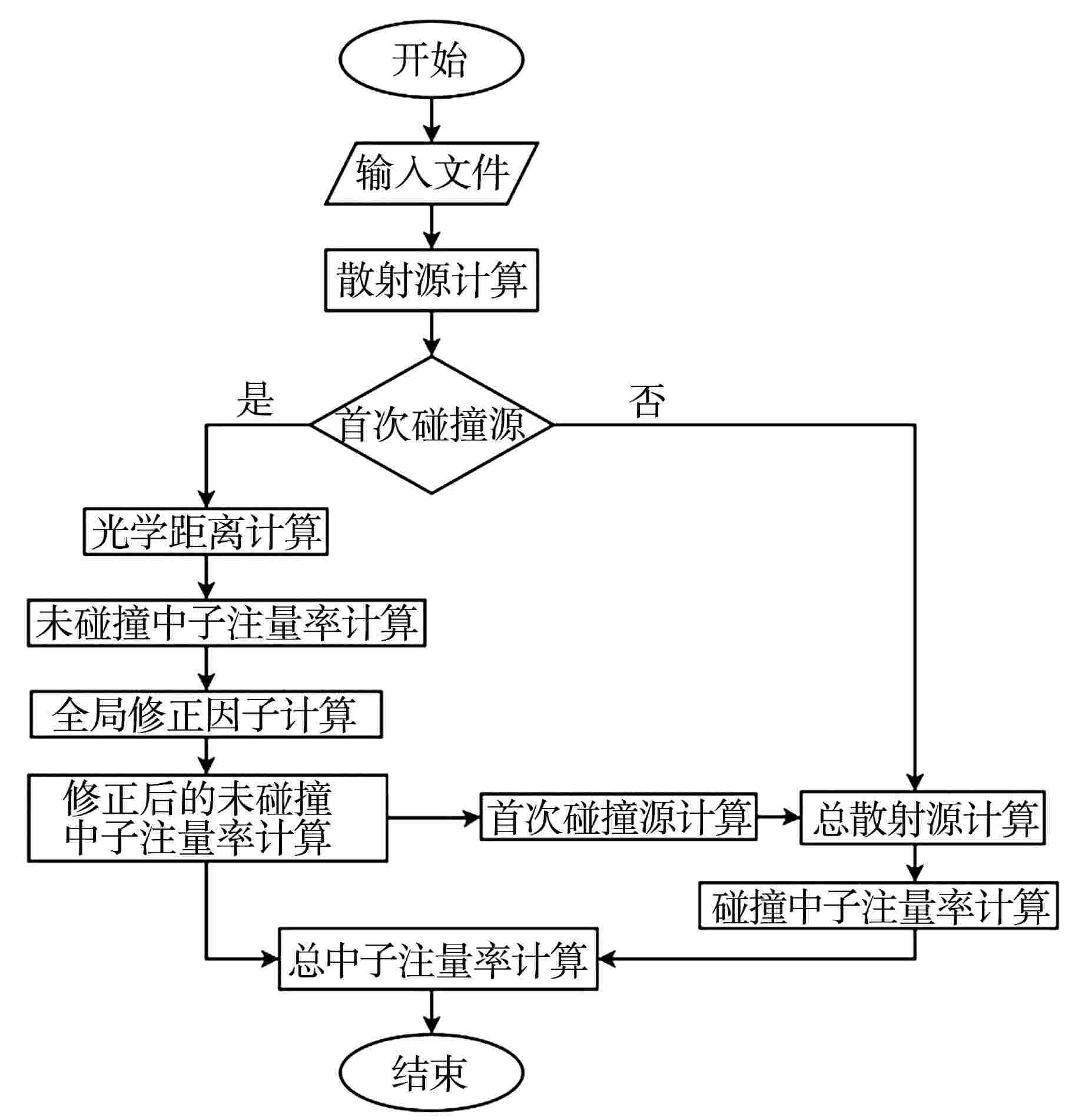
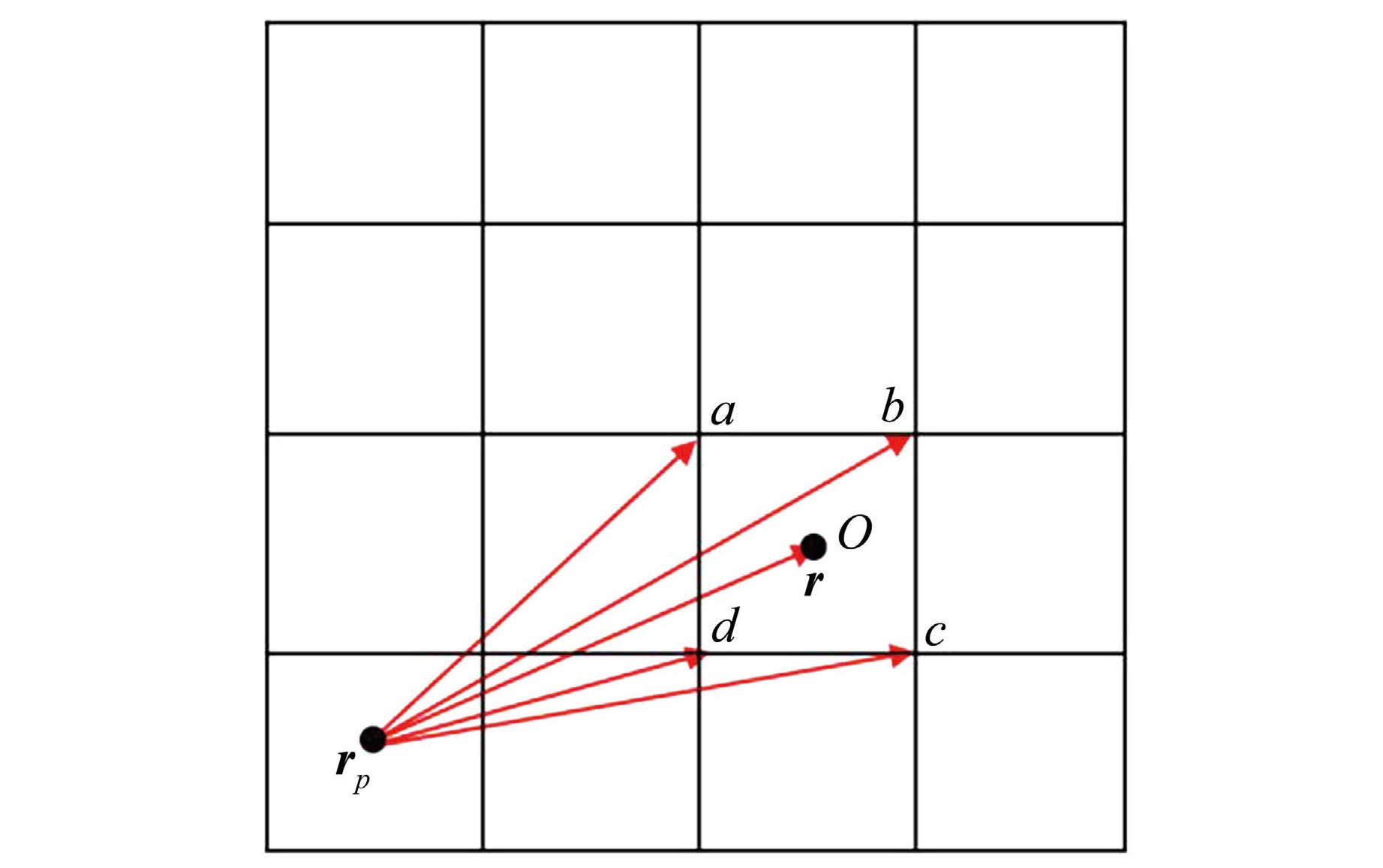
Research on Ray Effect Method Based on Global Factor Correction for First Collision Source
-
摘要: 计算孤立源、大空腔中子输运问题时，离散纵标方法（SN）存在射线效应，计算结果失真，常用首次碰撞源方法进行缓解以提高结果可靠性。但在首次碰撞源方法中，需要求解未碰撞中子注量率，通常采用基于网格中心法或网格角点平均值法的射线追踪技术，破坏了未碰撞中子数守恒原则。本文提出采用全局因子修正法对未碰撞中子注量率进行修正，使其满足中子数守恒原则；经过Kobayashi屏蔽计算基准题的检验，计算结果最大误差从6.15%降到3.71%，表明该方法能有效提高计算精度，可为屏蔽优化设计提供数据支持。
-
关键词:
- 全局因子 /
- 离散纵标方法（SN） /
- 首次碰撞源 /
- 射线效应
Abstract: In the calculation of neutron transport problems with spatially localized source or largely void region, the discrete ordinate method (SN) suffers from ray effects, which cause computational inaccuracies. The first collision source method is often used to alleviate the ray effect to improve the reliability of results. However, this method requires the calculation of the uncollided neutron flux. Generally, which is typically achieved through ray tracing technology based on the grid center method or the grid corner average method, destroying the conservation principle of the number of uncollided neutrons. In this paper, a global factor correction method is proposed to correct the uncollided neutron flux to meet the principle of neutron number conservation. Through the test of Kobayashi shielding calculation benchmark problem, the calculation results show that the maximum error is reduced from 6.15% to 3.71%, indicating that the method can effectively improve the accuracy of calculation results and provide data support for shielding optimization design.-
Key words:
- Global factor /
- Discrete ordinate method (SN) /
- First collision source /
- Ray effect
-
0. 引 言
堆内熔融物滞留（IVR）策略作为严重事故缓解措施，在多个三代核电设计中均有采用。IVR策略通过向压力容器外部的堆腔注水冷却压力容器壁面带走堆芯余热，保证压力容器的完整性[1]。同时，在严重事故管理中向一回路注水从压力容器内部带走堆芯余热也是重要的严重事故缓解措施。
这两项重要的严重事故缓解措施在严重事故管理后期可能存在矛盾，IVR策略运行可以将熔融物滞留在压力容器内，并在晚期形成熔融池，熔融池的集热效应可能使压力容器承压能力降低。如果在事故前期未能实现一回路注水，在IVR策略运行一段时间后，注水能力恢复，实施一回路再注水，注入的冷却水进入干涸的熔融池可能导致一回路压力快速上升，如果压力上升过高则有压力容器失效的风险。
本文参考某百万千瓦级核电厂设计对IVR策略投入后晚期（即压力容器下封头已形成熔融池的情况下）向干涸堆芯注水的工况开展分析，分析晚期再注水对一回路压力的影响，并针对严重事故管理策略提出建议。
1. 晚期再注水对IVR策略运行的影响
IVR策略通过反应堆压力容器外部冷却的方式将熔融物滞留在压力容器内。严重事故下影响压力容器结构完整性、IVR策略成功运行的主要因素有：堆芯熔融物温度、压力容器壁面的热流密度、堆芯熔融物质量、压力容器内部压力等。
如果执行晚期再注水，对于事故缓解的好处是可以带走熔融物热量、降低熔融物温度、减小壁面热流密度，但会增加堆芯熔融物质量、影响压力容器内部压力。其中，压力容器内部压力的增大将导致容器下封头的蠕变变形量显著增大，蠕变失效时间显著减小[2]。本文关注的是晚期再注水导致的一回路压力风险。
2. 实施再注水工况分析
本文所分析工况为实施再注水的IVR策略成功运行的严重事故晚期工况，根据IVR策略的运行要求可知，此时一回路处于充分泄压状态，一回路压力低于2 MPa，且堆芯熔融物已全部落入下封头并形成熔融池。
因此具体的始发事件对晚期再注水压力风险分析影响不大，根据分析需求，本文选取的事故序列为：丧失全部给水叠加多重安全功能失效事故，事故后操纵员根据信号开启严重事故专用泄压阀门并实施IVR策略。该事故下一回路没有其他破口，只通过严重事故专用泄压阀门泄压，对于晚期注水后的一回路压力响应分析是较为保守的。
在IVR策略成功运行的严重事故晚期向干涸的熔融池实施一回路再注水会造成一回路压力上升，实施注水时影响压力上升的速度和强度的主要因素有：注水时间、注水流量、严重事故专用泄压阀开启数量。因此本文在分析时将针对以上因素做影响研究，找出晚期注水造成一回路压力变化的规律。
压力风险分析步骤：①选择IVR策略成功投入并不实施严重事故晚期再注水的算例作为基础算例；②在基础算例之上，从下封头水蒸干开始，以10000 s为时间间隔对注水时间进行影响研究；③在分析得到的典型注水时间点上，对注水流量进行影响研究；④在分析得到典型的注水时间和注水流量的基础上，对开启严重事故专用泄压阀的数量进行影响研究。
3. 分析程序与假设
采用一体化严重事故分析程序MAAP，建立反应堆严重事故计算分析模型，包括反应堆堆芯、一回路系统、二回路系统、严重事故泄压系统、安全壳空间及相关的专设安全设施。分析时有以下主要假设：除安注箱外在实施一回路再注水前不考虑其他专设安全系统；操纵员按照规程开启严重事故专用泄压阀门并投入IVR。
4. 不实施再注水事故进程研究
分析不实施严重事故晚期再注水的事故进程，考虑的计算方案即方案1：丧失全部给水叠加多重安全功能失效事故，操纵员根据信号手动开启一列严重事故专用泄压阀、投入IVR策略，不实施严重事故晚期再注水，计算到240000 s结束。根据方案1的计算结果可看出，发生丧失全部给水事故后3686 s堆芯开始裸露，堆芯出口温度在4293 s达到650℃，操纵员开启一列阀门泄压，因为没有冷却剂补充，熔融物在11794 s向下封头迁移，下封头的水在13098 s蒸干，压力容器内部压力在下封头水蒸干后很快与安全壳压力达到平衡（图1）。约33589 s下封头内熔融物质量达到稳定值，全部熔融物进入下封头，认为此时刻为下封头稳定熔融池形成时刻（图2）。下封头内熔融物的整体温度在下封头熔融池形成后便达到最高值，然后随着衰变热降低而缓慢降低（图3），但熔融物表面的温度因为前期有水冷却，最高温度出现的时间较熔融池形成晚，最高温度出现在约50000 s附近，因为计算程序取不到熔融池表面温度，此处用下封头内气体温度表示温度变化趋势（图4）。
图 3 方案1下封头熔融池整体温度Figure 3. Overall Temperaure of Lower Head Melting Pool for Scheme 15. 实施再注水压力风险研究
5.1 晚期再注水时间影响研究
晚期再注水的时间影响研究从下封头的水蒸干后以10000 s为时间间隔进行计算。同样流量注入导致的一回路升压大小与熔融池的温度有关，所以针对温度较高的时间段即对事故后80000 s之前进行注水开展研究。采用典型的注水流量一列低压安注流量进行计算。计算方案如下：
方案a~g：在方案1的基础上，事故后20000 s/30000 s/40000 s/50000 s/60000 s/70000 s/80000 s实施一列低压安注补水，共7个序列。
图5给出了方案 a~g的压力容器内压力变化示意图，方案a~g的压力容器内压力峰值见表1。
图 5 方案 a~g压力容器内压力示意图Figure 5. Schematic Diagram of Pressure in Pressure Vessel of Schemes a~g表 1 方案a~g的压力容器内压力峰值Table 1. Pressure Peak of Pressure Vessel of Schemes a~g分析方案 注水时间/s 压力峰值出现时间/s 压力峰值/MPa a 20000 20661 2.70 b 30000 30645 4.28 c 40000 40638 4.66 d 50000 50642 4.69 e 60000 60635 4.58 f 70000 70655 4.46 g 80000 80621 4.26 根据计算结果可以看出，在严重事故晚期向干涸的熔融池注水会产生大量蒸汽导致压力容器内压力快速上升，在熔融物被淹没后压力下降，形成压力峰。根据分析结果可以看出，事故后50000 s时向压力容器内注水产生的压力峰值（4.69 MPa）最高，对比第4节的下封头内气体温度（熔融池表面温度）的变化趋势可以看出，注水时刻的熔融池表面温度越高，瞬间蒸发的水蒸气量越大，导致的压力峰也越高，所以注水时间对压力峰的影响主要与注水时刻的熔融池表面温度相关。
5.2 晚期再注水流量影响研究
根据注水时间影响研究结果，在方案d注水时刻为50000 s时会出现最高的压力峰。在此基础上对注水流量的影响进行研究。严重事故管理遵循能用则用的原则，在严重事故晚期恢复注水的途径有多种可能性，在分析时考虑各种典型的注水途径，采用的分析方案如下，根据注水流量从高到低排序：
方案d1~d4：在方案d的基础上变更注水流量，事故后50000 s实施两列低压安注/两列中压安注/一列中压安注/临时补水。
表2给出了方案d1~d4在实施注水后的一回路压力峰值。根据方案d1~d4的结果及与方案d的对比可以看出，在事故后50000 s以一列低压安注实施晚期再注水（方案d）产生的压力峰是最高的。
表 2 方案d1~d4的压力容器内压力峰值Table 2. Pressure Peak of Pressure Vessel of Schemes d1~d4方案 注水时间/s 注水途径 压力峰值/MPa 压力峰持续时间①/s d1 50000 两列低压安注 4.47 1069 d 一列低压安注 4.69 1145 d2 两列中压安注 3.32 1533 d3 一列中压安注 3.05 1909 d4 临时补水 1.72 2317 注：①注水后一回路压力高于1 MPa的持续时间 从计算结果可知，大致规律是注水流量越高产生的压力峰值越高，注水流量越小压力峰的持续时间越长。注水流量从两方面影响注水后的压力峰：①注水后瞬间产生的蒸汽导致的压力上升；②再淹没熔融物后的冷却降压。由于一列低压安注的注水流量已经足够大，增加到两列低压安注流量后由于注入水的冷却作用更明显，其压力峰值并未超过一列低压安注注入的情况。
5.3 阀门开启数量影响研究
严重事故专用泄压系统设置了两列泄压阀门，在前面的分析中都只考虑开启一列缷压阀门的工况，为限制晚期注水的压力上升，可考虑提前开启两列泄压阀门。根据5.1节的分析结果，在方案d的基础上将对开启两列快速泄压阀的情况开展研究。分析采用计算方案如下：
方案d5：在方案d（事故后50000 s实施一列低压安注补水）的基础上，开启两列严重事故专用泄压阀。
表3给出了方案d和方案d5在实施注水后的一回路压力峰值。
表 3 方案d、方案d5的压力容器内压力峰值Table 3. Pressure Peak of Pressure Vessel of Scheme d/d5方案 注水时间/s 注水途径 开启严重事故专用
泄压阀门数量压力峰值/MPa d 50000 一列低压安注 一列 4.47 d5 两列 2.57 根据计算结果对比可知，开启两列严重事故专用泄压阀可以有效降低晚期注水后的压力峰值。
6. 结论及建议
本文研究了在IVR策略成功的工况下实施晚期堆芯注水时一回路的压力变化，分析了各种注水策略包括注水时间、注水流量、泄压各因素对压力变化的影响。得到以下结论以及严重事故管理建议：
在实施IVR策略的严重事故晚期恢复一回路再注水会导致一回路压力上升，产生压力峰，可能威胁压力容器完整性；建议在IVR策略成功并可能存在干涸熔融池的工况下禁止向压力容器内注水。
如果出于某种原因，如IVR策略无法维持运行而此时有向压力容器内注水的能力，需要实施压力容器内的再注水，可以从两方面降低晚期再注水的压力风险：①先实施小流量注入降低熔融池表面温度，再后续调整注水流量至可以带走熔融物温度的流量；②提前开启两列严重事故专用泄压阀实施充分的泄压，以降低晚期再注水造成的超压风险。
-
表 1 截面参数
Table 1. Section Parameters
区域 源强 /(cm−3·s−1) 宏观总截面/cm−1 宏观散射截面/ cm−1 源区 1 0.1 0.05 真空区 0 0.0001 0.00005 屏蔽区 0 0.1 0.05 
下载: 导出CSV
表 2 不同离散角度下的 JSNT-S 直接计算结果
Table 2. Calculation Results of JSNT-S at Different Discrete Angle
位置坐标/cm 中子注量率/(cm−2·s−1) 误差/% 参考解 S8 S12 S16 S8 S12 S16 (5, 5, 5) 8.293×100 8.389×100 8.309×100 8.292×100 1.16 0.19 0 (15,15,15) 6.632×10−1 6.614×10−1 6.121×10−1 6.081×10−1 −0.27 −7.7 −8.32 (25,25,25) 2.688×10−1 2.087×10−1 3.169×10−1 2.905×10−1 −22.36 17.88 8.06 (35,35,35) 1.567×10−1 2.052×10−1 2.144×10−1 1.337×10−1 30.94 36.85 −14.66 (45,45,45) 1.044×10−1 2.008×10−1 1.373×10−1 9.749×10−2 92.29 31.5 −6.63 (55,55,55) 3.021×10−2 8.466×10−2 2.500×10−2 3.101×10−2 180.23 −17.24 2.64 (65,65,65) 4.066×10−3 1.515×10−2 2.534×10−3 4.686×10−3 272.65 −37.68 15.26 (75,75,75) 5.861×10−4 2.718×10−3 3.345×10−4 6.726×10−4 363.77 −42.94 14.75 (85,85,85) 8.661×10−5 4.753×10−4 4.935×10−5 9.518×10−5 448.76 −43.03 9.9 (95,95,95) 1.129×10−5 8.038×10−5 5.795×10−6 1.204×10−5 611.99 −48.68 6.66
下载: 导出CSV
表 3 JSWT-S与FCS、FCS-C中子注量率计算结果与误差
Table 3. Calculation Results and Errors of Neutron Flux Rates for JSNT-S, FCS and FCS-C
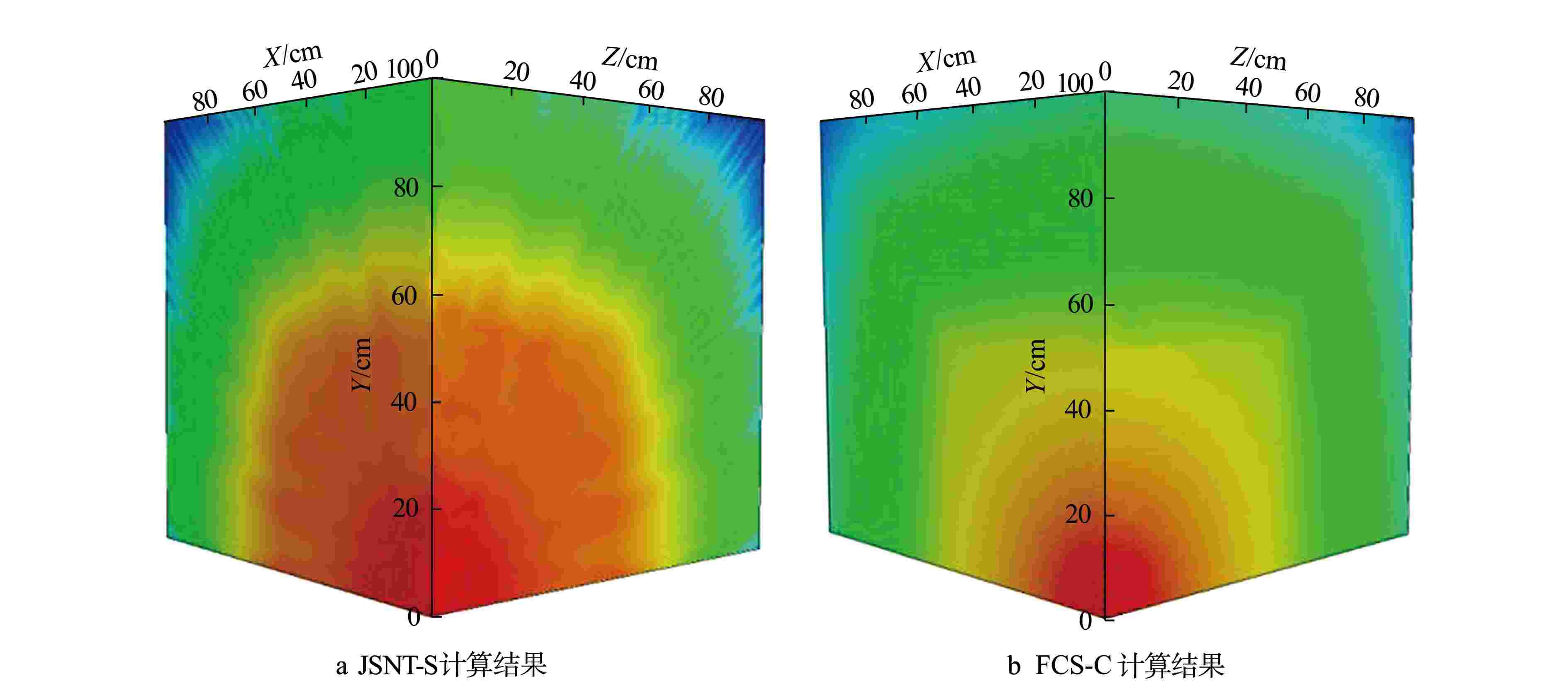
位置坐标/cm 中子注量率/(cm−2·s−1) 误差/% 参考解 JSNT-S FCS FCS-C JSNT-S FCS FCS-C (5, 5, 5) 8.293×100 8.292×100 8.132×100 8.274×100 0 −1.94 0.23 (15,15,15) 6.632×10−1 6.081×10−1 6.429×10−1 6.549×10−1 −8.32 −3.06 1.25 (25,25,25) 2.688×10−1 2.905×10−1 2.690×10−1 2.745×10−1 8.06 0.08 −2.13 (35,35,35) 1.567×10−1 1.337×10−1 1.470×10−1 1.509×10−1 −14.66 −6.15 3.71 (45,45,45) 1.044×10−1 9.749×10−2 1.016×10−1 1.042×10−1 −6.63 −2.7 0.14 (55,55,55) 3.021×10−2 3.101×10−2 2.877×10−2 2.949×10−2 2.64 −4.77 2.38 (65,65,65) 4.066×10−3 4.686×10−3 4.077×10−3 4.159×10−3 15.26 0.29 −2.3 (75,75,75) 5.861×10−4 6.726×10−4 5.872×10−4 5.985×10−4 14.75 0.18 −2.12 (85,85,85) 8.661×10−5 9.518×10−5 8.582×10−5 8.747×10−5 9.9 −0.91 −0.99 (95,95,95) 1.129×10−5 1.204×10−5 1.116×10−5 1.137×10−5 6.66 −1.18 −0.71
下载: 导出CSV
-
[1] BATISTELA C H F, VILHENA M T D, BORGES V. Determination of the effective multiplication factor in a slab by the LTSN method[J]. Annals of Nuclear Energy, 1999, 26(9): 761-767. doi: 10.1016/S0306-4549(98)00096-6 [2] 闫宇航. 反应堆压力容器快中子注量计算方法研究[D]. 上海: 上海交通大学, 2012: 9-12. [3] 杨寿海,陈义学,王伟金,等. 三维离散纵标方法在RPV快中子注量率计算中的初步应用[J]. 核科学与工程,2011, 31(4): 294-298. [4] XU L F, CAO L Z, ZHENG Y Q, et al. Development of a new parallel SN code for neutron-photon transport calculation in 3-D cylindrical geometry[J]. Progress in Nuclear Energy, 2017, 94: 1-21. doi: 10.1016/j.pnucene.2016.09.005 [5] 谢仲生, 邓力. 中子输运理论数值计算方法[M]. 西安: 西安交通大学出版社, 2022: 142-149. [6] MASUKAWA F, KADOTANI H, HOSHIAI Y, et al. GRTUNCL-3D: An extension of the GRTUNCL code to compute R-θ-Z first collision source moments[J]. Journal of Nuclear Science and Technology, 2000, 37(S1): 471-474. [7] KOSAKO K, KONNO C. FNSUNCL3: First collision source code for TORT[J]. Journal of Nuclear Science and Technology, 2000, 37(S1): 475-478. [8] 刘永康, 胡永明. 首次碰撞源方法减弱射线效应[C]//第十一届反应堆数值计算和粒子输运学术会议暨2006年反应堆物理会议. 哈尔滨: 哈尔滨工程大学, 2006. [9] 胡也,陈义学,张斌,等. 基于首次碰撞源方法的多维SN射线效应研究[J]. 原子能科学技术,2013, 47(S1): 9-14. [10] 陈蒙腾,陈义学,张斌,等. ARES屏蔽程序中二维射线效应消除方法研究[J]. 原子能科学技术,2013, 47(S2): 700-706. [11] 潘承勇. 浅谈勒让德-高斯数值积分在工程中的应用[J]. 黑龙江交通科技,2021, 44(7): 188-189. doi: 10.3969/j.issn.1008-3383.2021.07.114 [12] 杨超,于涛,邓力,等. 三维并行首次碰撞源模块研制[J]. 核动力工程,2021, 42(2): 39-42. doi: 10.13832/j.jnpe.2021.02.0039 [13] KOBAYASHI K, SUGIMURA N, NAGAYA Y. 3D radiation transport benchmark problems and results for simple geometries with void region[J]. Progress in Nuclear Energy, 2001, 39(2): 119-144. doi: 10.1016/S0149-1970(01)00007-5 -
下载:
计量
- 文章访问数: 197
- HTML全文浏览量: 60
- PDF下载量: 21
- 被引次数: 0
