Multi-fidelity Mechanical Model Matching and Updating of Primary Loop Supporting Structure
-
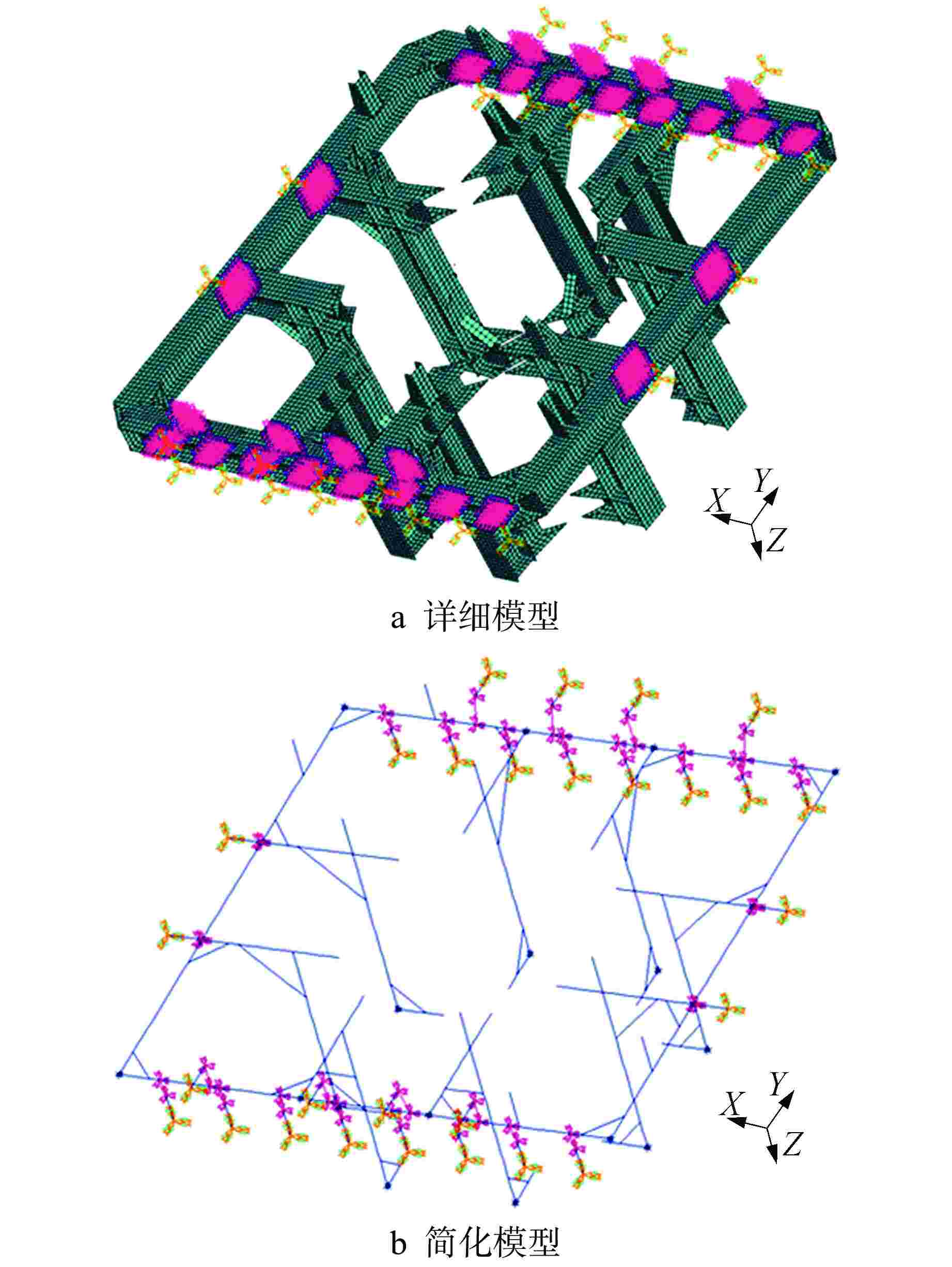
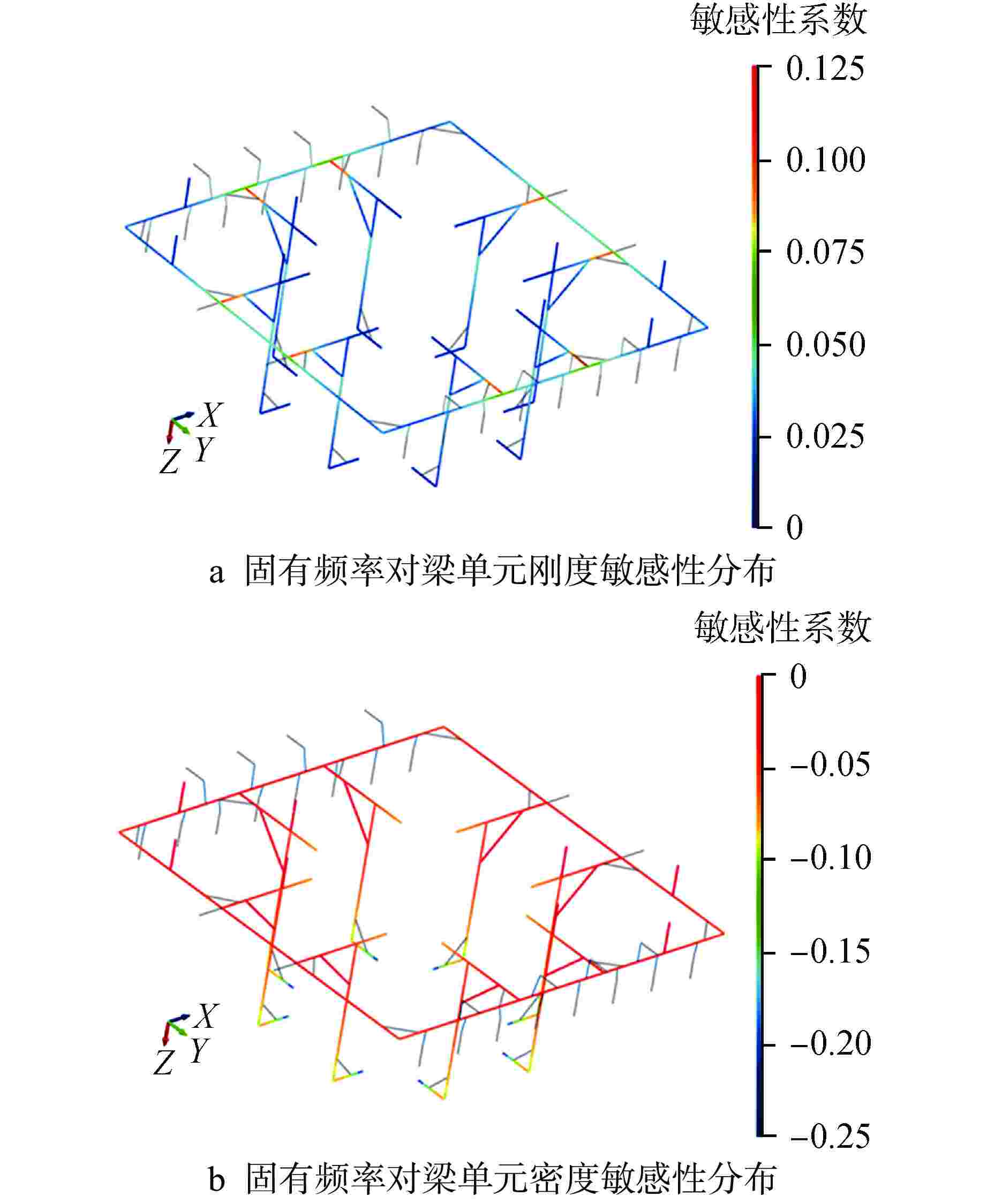
摘要: 反应堆及一回路系统整体支承结构设计需同时满足减振和抗冲击的力学要求，相应地需建立不同保真度的力学模型。首先应用相关性分析，对反应堆及一回路系统整体支承结构多保真度力学模型（包括高保真度力学模型和低保真度力学模型）的静力和动力特性匹配性进行了定量研究；然后应用贝叶斯参数估计方法对低保真度力学模型（简化模型）进行模型更新，以提高其与高保真度力学模型（详细模型）的匹配性。本文所提出的多保真度力学模型间的匹配和单向更新策略为后续结构力学性能多目标优化奠定了基础。Abstract: The design of reactor primary loop support should meet the vibration reduction and anti-shock requirements. Accordingly, mechanical models with different fidelity should be established. This paper first adopted correlation analysis to quantify the compatibility of static and dynamical characters of multi-fidelity mechanical models (including high-fidelity and low-fidelity models) of the reactor and primary loop supporting structure. Then, Bayesian parameter estimation technique was applied to update the low-fidelity model (simplified model) to increase its compatibility to high-fidelity model (detailed model). The model matching and updating strategy proposed by this paper lays the foundation for future multi-objective optimization of support structure mechanical properties.
-
图 1 分散式布置的一回路系统及其支承结构
Figure 1. Distributed Primary Loop System and Its Supporting Structure
图 2 整体支承结构多保真度力学模型
Figure 2. Multi-fidelity Mechanical Model of the Supporting Structure
图 3 多保真度力学模型MAC分布与固有频率对照
Figure 3. MAC Distribution and Natural Frequencies of Multi-fidelity Mechanical Model
图 4 简化模型固有频率对不同参数的敏感性
Figure 4. Sensitivity of Natural Frequency to Different Parameters of Simplified Model
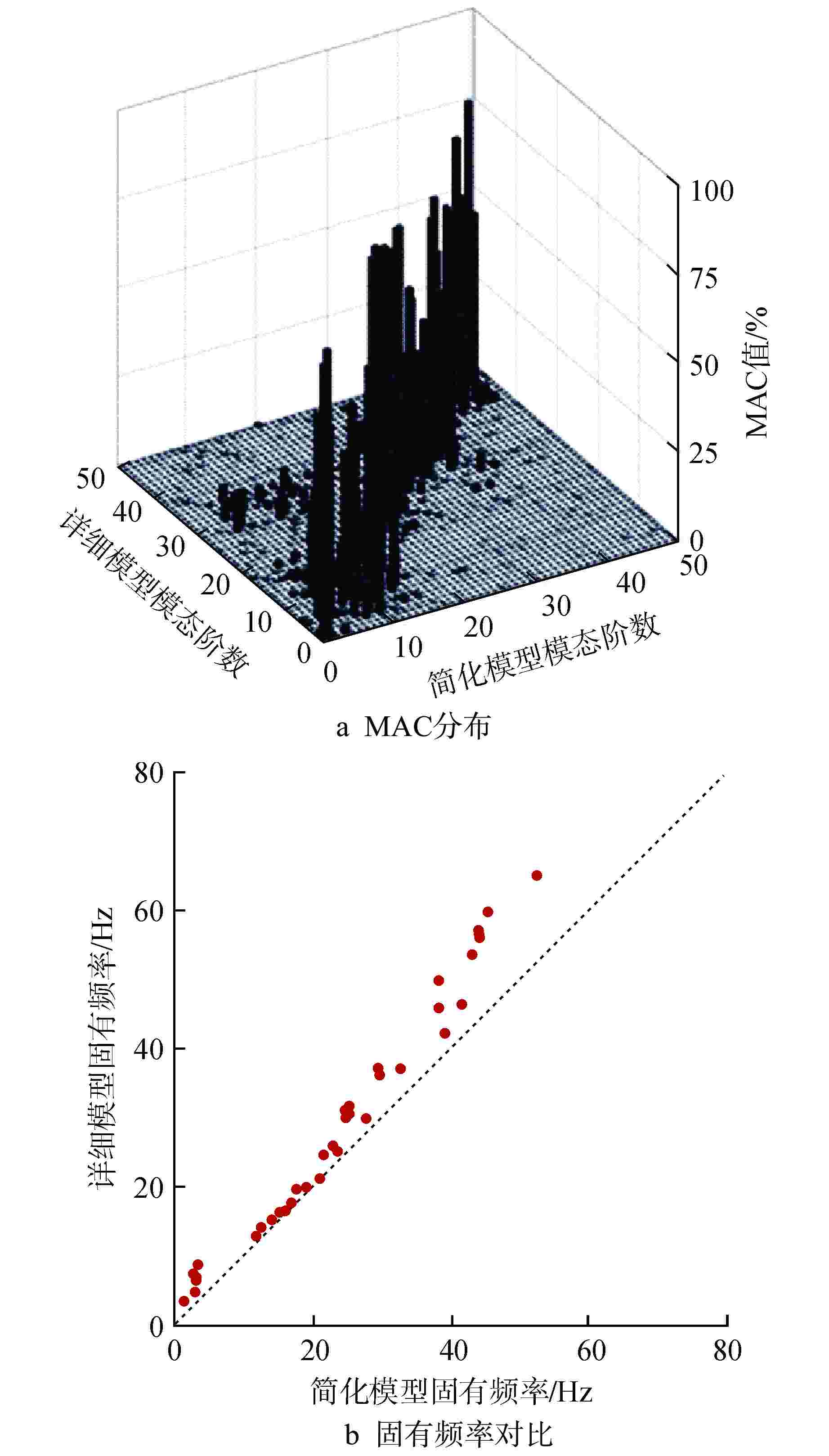
表 1 简化模型更新后模态匹配情况
Table 1. Matched Modes of Updated Simiplified Model
简化模
型阶数简化模型固有频
率/Hz详细模
型阶数详细模型固有频
率/Hz固有频率
偏差/%MAC/% 21 12.316 1 12.895 −4.49 81.7 22 13.403 2 14.184 −5.51 80.4 23 15.284 3 15.341 −0.37 89.1 24 16.116 4 16.521 −2.45 81.4 25 17.079 5 16.790 1.72 91.5 26 17.894 7 19.770 −9.49 40.0 27 18.633 6 17.872 4.26 58.3 28 19.740 8 20.066 −1.62 67.5 30 20.694 9 21.257 −2.65 53.7 
下载: 导出CSV
表 2 更新后简化模型和详细模型配对模态各向有效质量对比
Table 2. Comparison of Modal Effective Mass at All Directions between Simplified Model and Detailed Model
简化模型配对模态有效质量分布/% 详细模型配对模态有效质量分布/% 模态阶数 X Y Z 模态阶数 X Y Z 21 10.80 0.04 6.07 1 8.78 0.07 0.07 22 2.79 0.03 39.47 2 0.05 0 45.95 23 0.33 1.86 0.12 3 0 0.35 0.1 24 0.16 52.18 0.99 4 0.39 55.90 0 25 53.07 0.09 0.03 5 51.76 0.46 0 26 0.06 0.18 3.61 6 0.02 0 14.37 27 0.32 7.06 6.43 7 0.03 0.21 0.37 28 0 0.34 3.25 8 0.02 0.24 0.47 30 0.30 0.54 0.31 9 0 0 0.10
下载: 导出CSV
-
[1] YU W B, HODGES D H, VOLOVOI V, et al. On Timoshenko-like modeling of initially curved and twisted composite beams[J]. International Journal of Solids and Structures, 2002, 39(19): 5101-5121. doi: 10.1016/S0020-7683(02)00399-2 [2] PALACIOS R, CEA A. Nonlinear modal condensation of large finite element models: application of Hodges’s intrinsic theory[J]. AIAA Journal, 2019, 57(10): 4255-4268. doi: 10.2514/1.J057556 [3] KAPANIA R K, LIU Y H. Static and vibration analyses of general wing structures using equivalent-plate models[J]. AIAA Journal, 2000, 38(7): 1269-1277. doi: 10.2514/2.1098 [4] FRISWELL M I, MOTTERSHEAD J E. Finite element model updating in structural dynamics[M]. London: Kluwer Academic Publishers, 1995: 12-16. [5] 国防科学技术工业委员会. 潜艇核动力装置设计安全规定 潜艇反应堆结构及设备抗冲击设计要求: GJB 843.31-97[S]. 北京: 中国标准出版社, 1997: 4. -
计量
- 文章访问数: 210
- HTML全文浏览量: 76
- PDF下载量: 41
- 被引次数: 0
