High-fidelity Full Core Neutronics Calculation Method for Fuel Assembly Bowing and Its Application
-
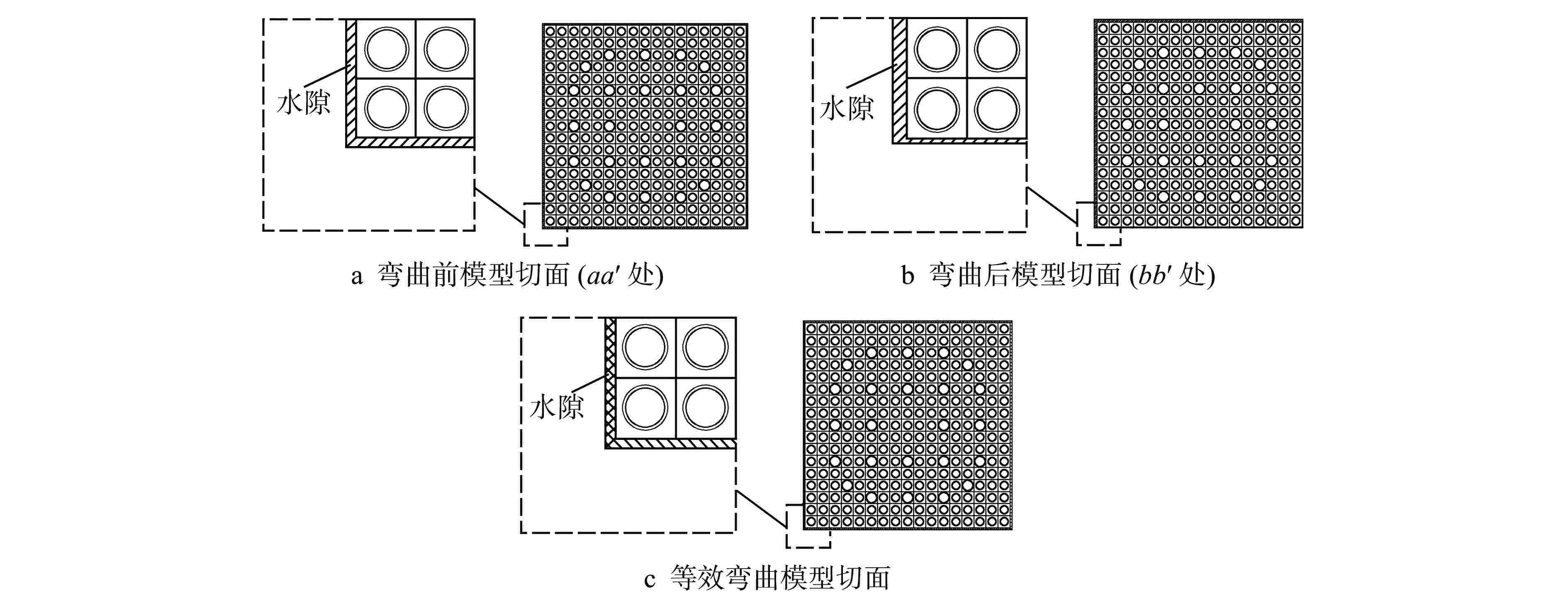
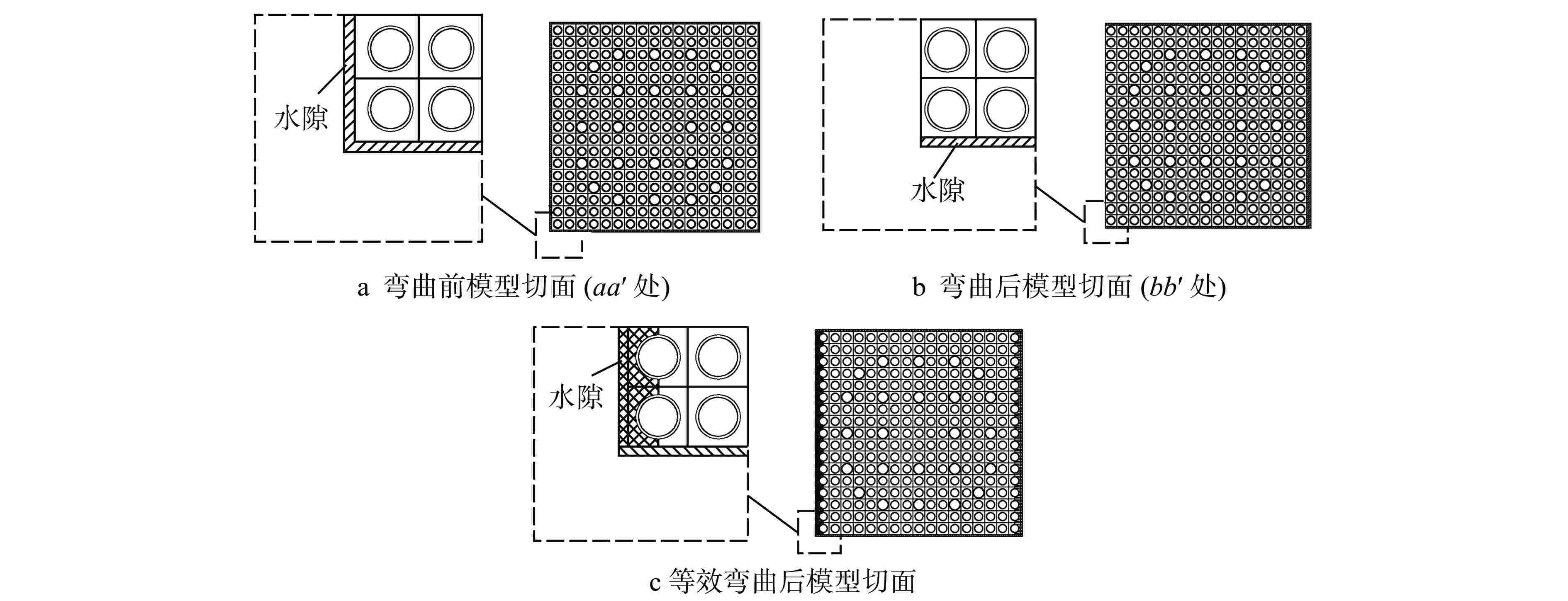
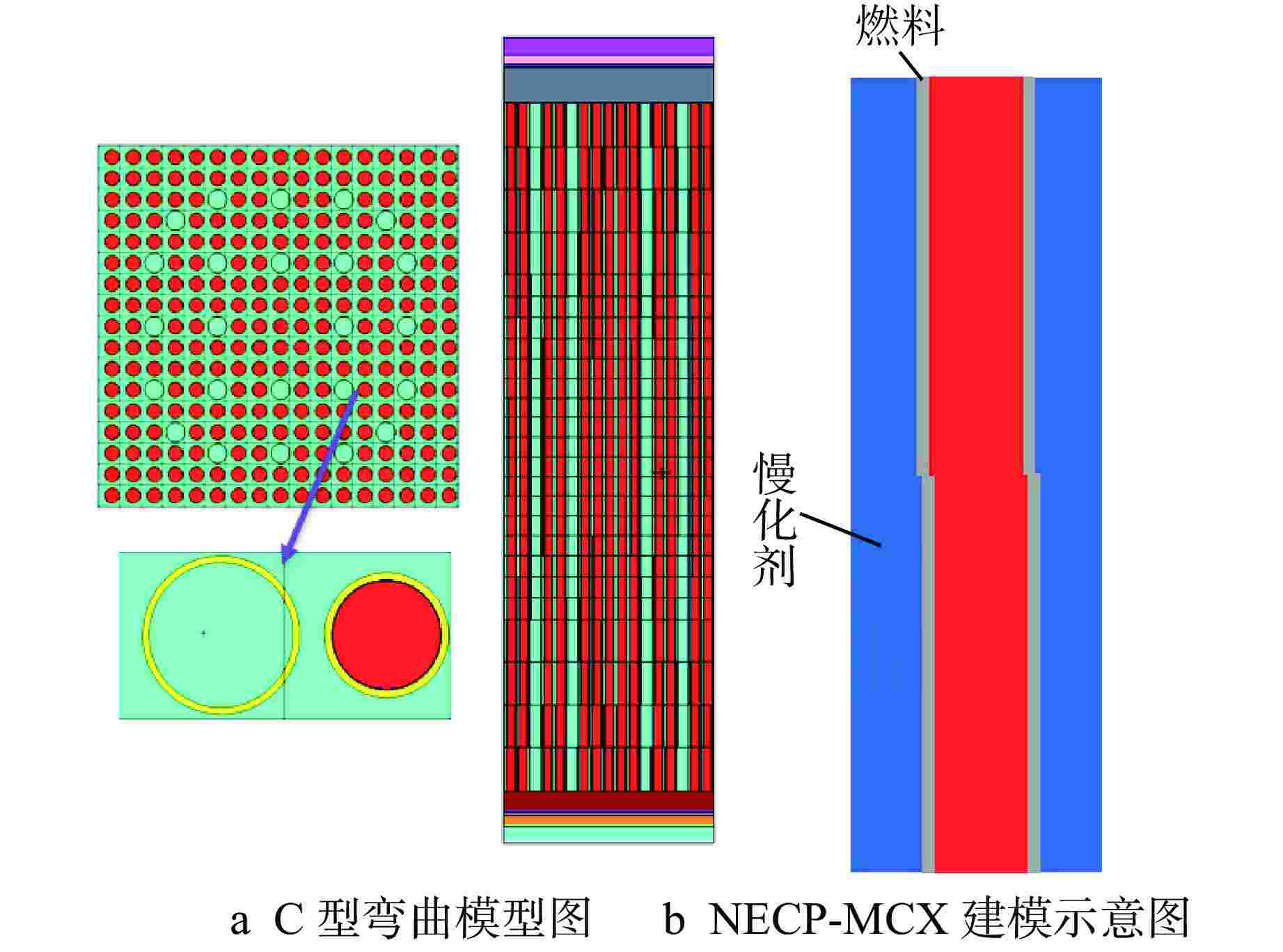
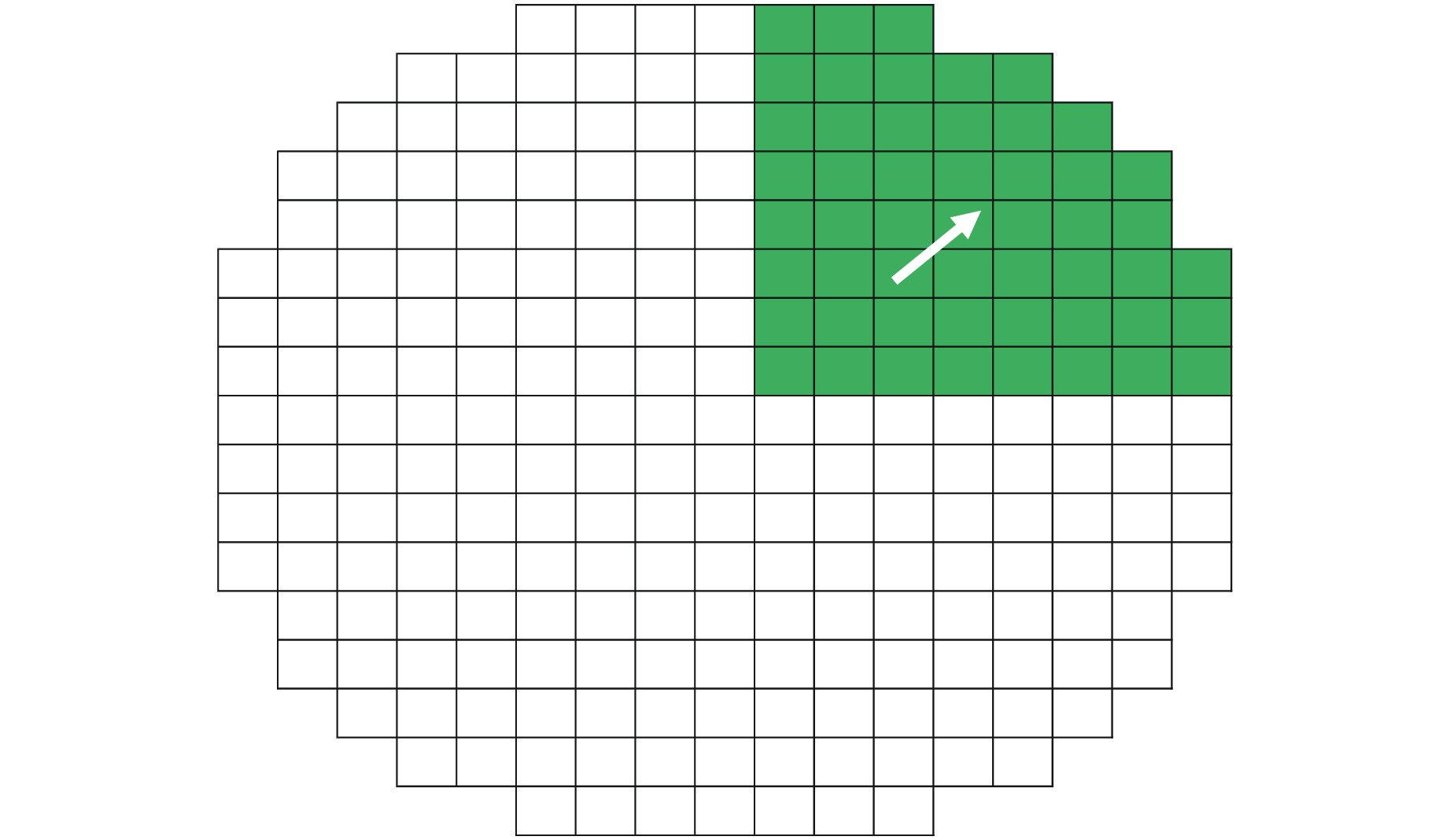
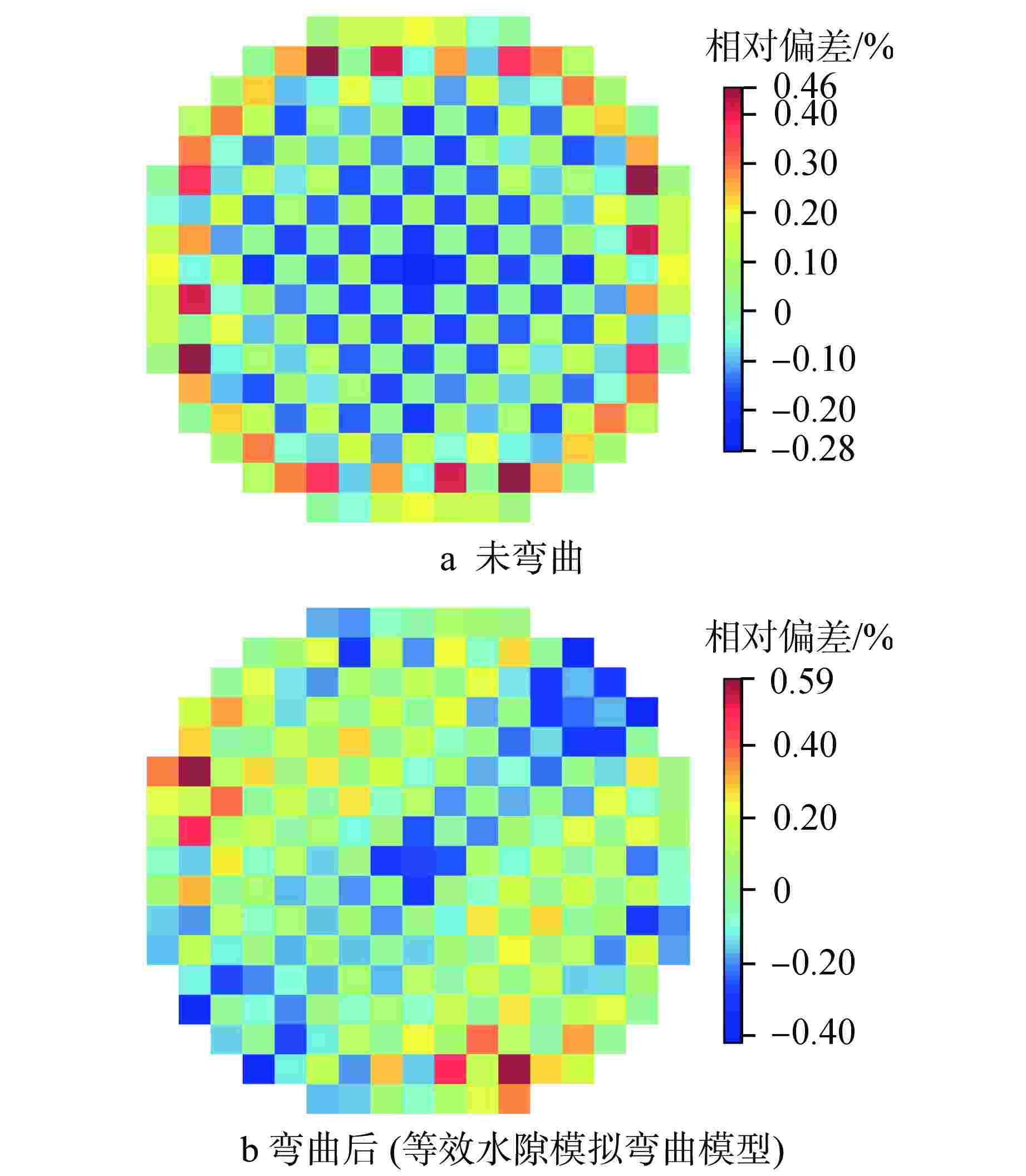
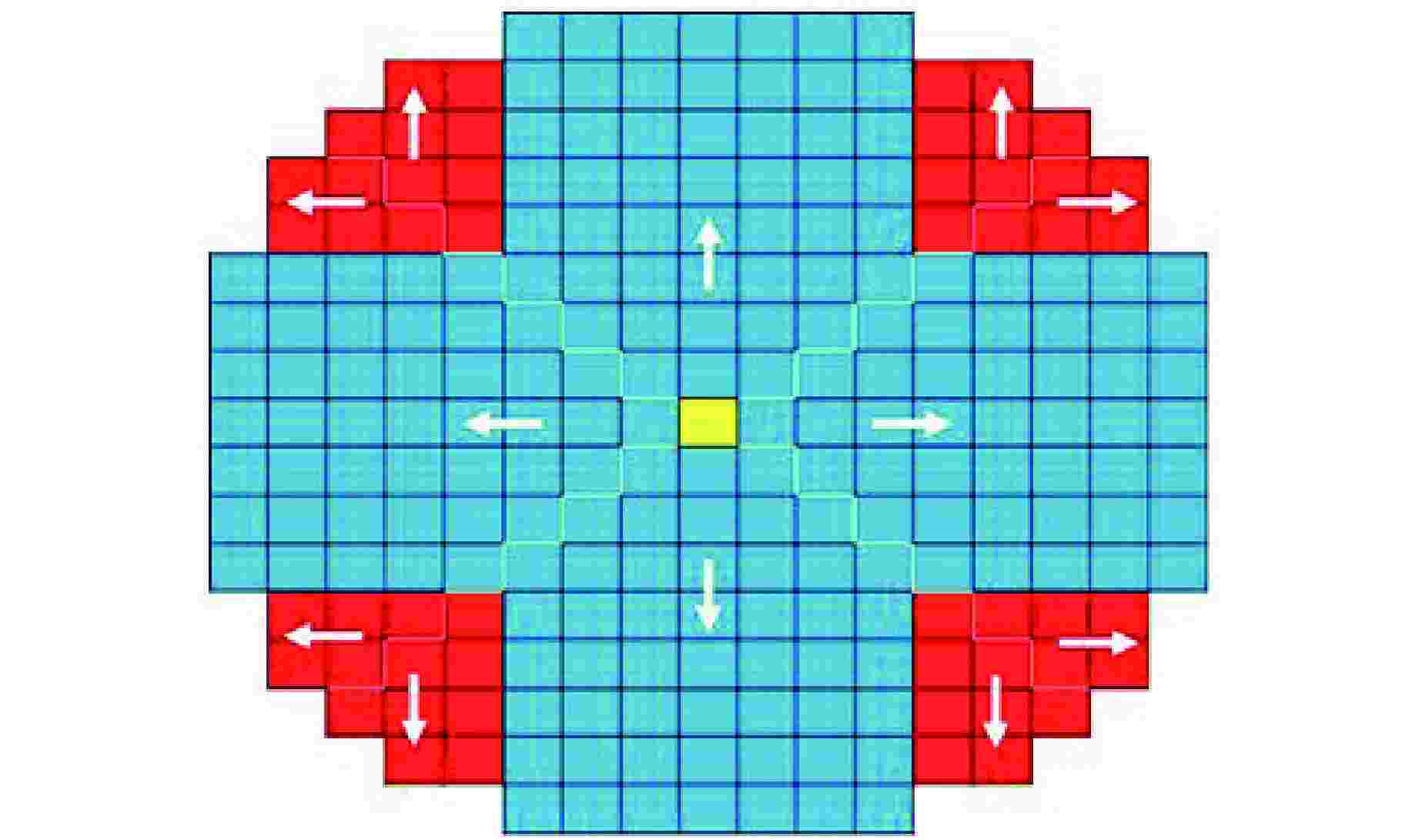
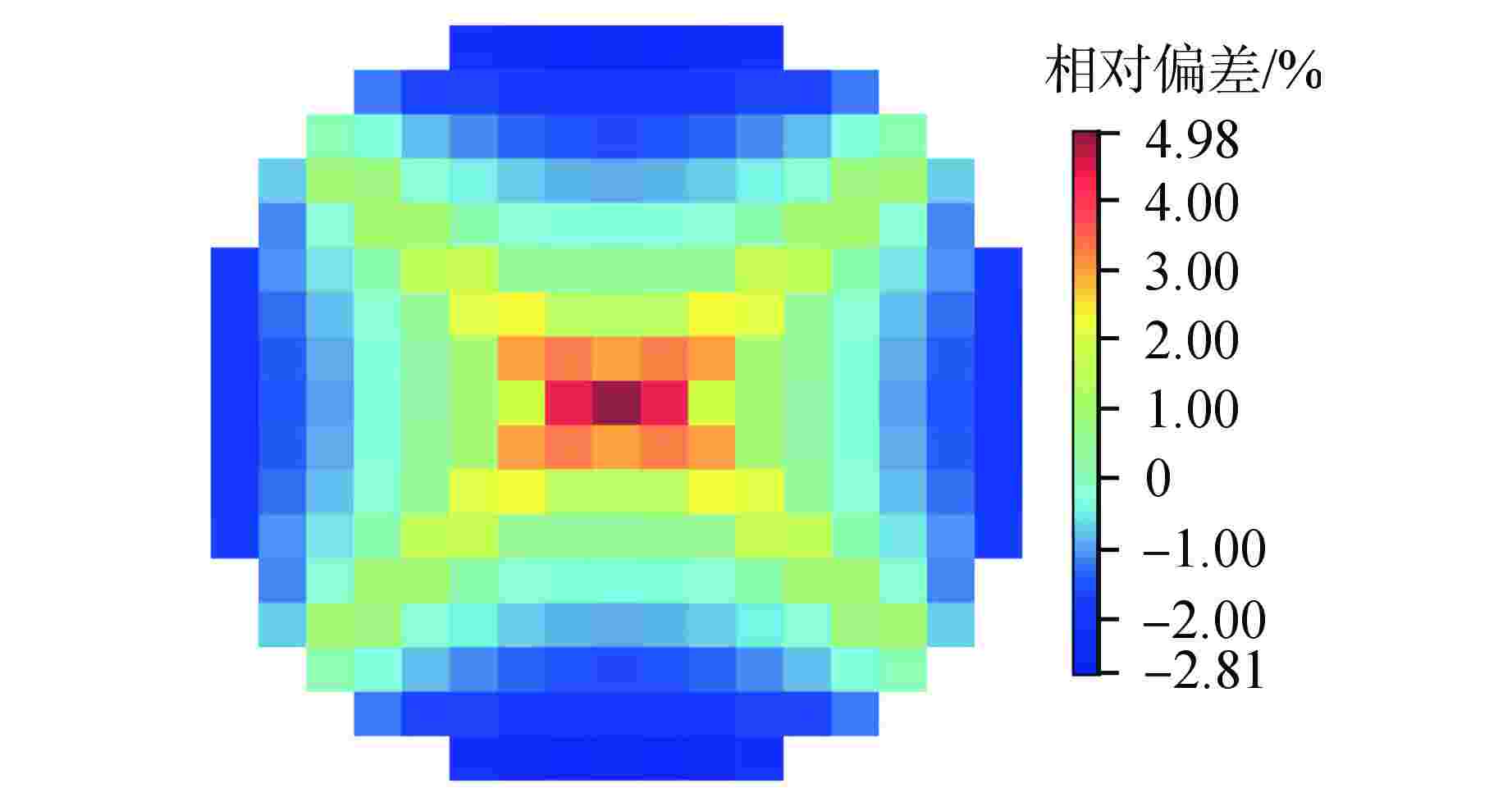
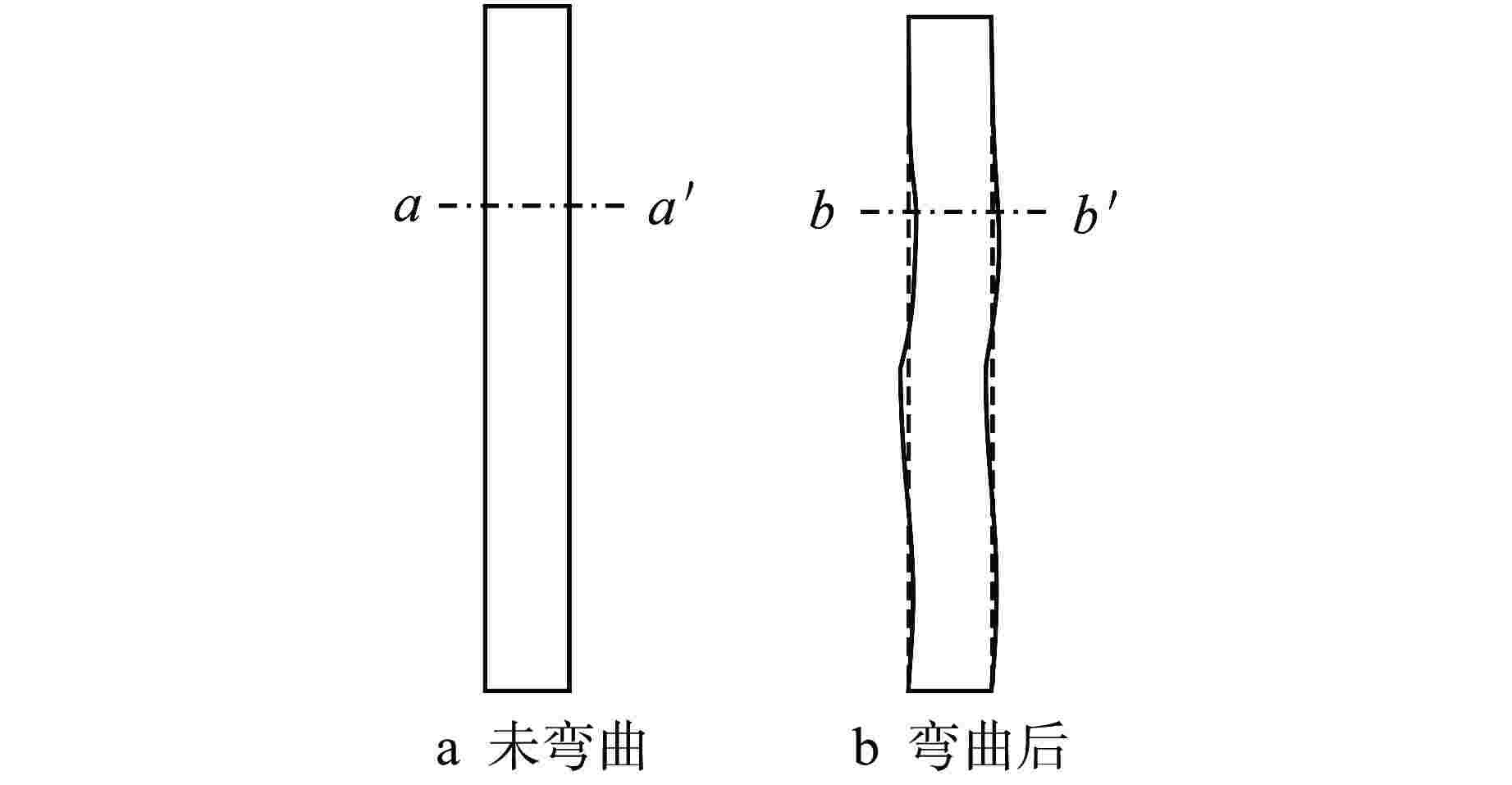
摘要: 为了研究燃料组件弯曲变形对堆芯功率分布的影响，提出了一种等效模拟压水堆堆芯内燃料组件弯曲的方法，即根据弯曲前后燃料组件四周的水隙材料的原子数目守恒原则，通过保持弯曲前后的水隙宽度不变，改变弯曲后水隙内所有核素的原子核密度，近似等效燃料组件弯曲后四周水隙的变化。通过蒙特卡罗程序NECP-MCX和确定论数值反应堆程序NECP-X对其正确性进行验证，并基于NECP-X程序对欧洲先进压水堆（EPR）全堆芯的燃料组件弯曲工况进行了模拟分析，计算结果表明：由于局部慢化效应变化，燃料组件小幅弯曲对堆芯功率分布影响相对较大，全堆芯问题中最大的偏移量在2 mm左右时可使组件功率的相对变化达到5%左右。
-
关键词:
- 组件弯曲 /
- 功率分布 /
- 蒙特卡罗程序 /
- 确定论程序 /
- 欧洲先进压水堆（EPR）
Abstract: In order to study the influence of bowing deformation of fuel assemblies on core power distribution, this paper proposes an equivalent method for simulating the bowing of fuel assemblies in PWR Core. That is, according to the principle of conservation of atomic number of the water gap material around the fuel assembly before and after bowing, the nuclear density of all nuclides in the water gap after bowing is changed by keeping the width of the water gap unchanged before and after bowing, which approximates the change of the water gap around the equivalent fuel assembly after bowing. Its correctness is verified by Monte-Carlo code NECP-MCX and deterministic numerical code NECP-X. Based on the deterministic numerical code NECP-X, the fuel assembly bowing condition of the EPR core is simulated and analyzed. The calculation results show that due to the change of local moderating effect, the small bending of fuel assembly has a relatively great influence on the core power distribution. When the maximum offset in the whole core problem is about 2mm, the relative change of the assembly power can reach about 5%.-
Key words:
- Fuel assembly bowing /
- Power distribution /
- Monte-Carlo code /
- Deterministic code /
- EPR
-
图 1 燃料组件弯曲前后轴向示意图
Figure 1. Axial Schematic Diagram of Fuel Assembly Before and After Bowing
图 2 燃料组件弯曲前后建立等效模型流程图
Figure 2. Flow Chart of Establishing Equivalent Model of Fuel Assembly Before and After Bowing
图 3 燃料组件过度弯曲前后建立等效模型流程图
Figure 3. Flow Chart of Establishing Equivalent Model of Fuel Assembly Before and After Excessive Bowing
图 4 燃料组件弯曲前后相对位置示意图
Figure 4. Schematic Diagram of Relative Position of Fuel Assembly Before and After Bowing
图 5 燃料组件弯曲前后内部示意图
Figure 5. Schematic Diagram of Internal Fuel Assembly Before and After Bowing
图 6 NECP-X程序计算等效水隙模拟弯曲模型与实际建模弯曲后模型径向功率偏差
Figure 6. Radial Power Deviation Between Equivalent Water Gap Simulated Bowing Model and Actual Bowing Model Using NECP-X
图 8 NECP-X与NECP-MCX程序计算得到的燃料棒径向功率偏差（算例4）
Figure 8. Radial Power Deviation of Fuel Rods Calculated by NECP-X and NECP-MCX (Case 4)
图 10 NECP-X与NECP-MCX程序计算得到的燃料棒径向功率偏差（算例5）
Figure 10. Radial Power Deviation of Fuel Rods Calculated by NECP-X and NECP-MCX (Case 5)
表 1 有效增殖因数计算结果
Table 1. Calculation Results of Effective Multiplication Factor
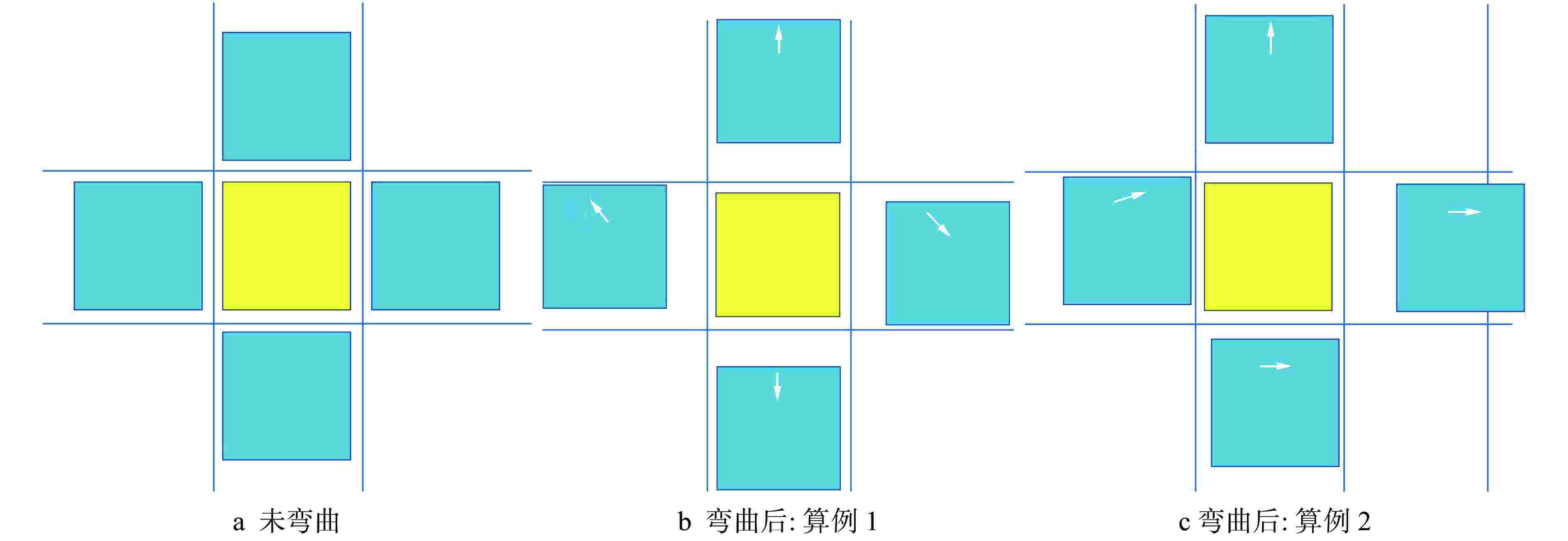
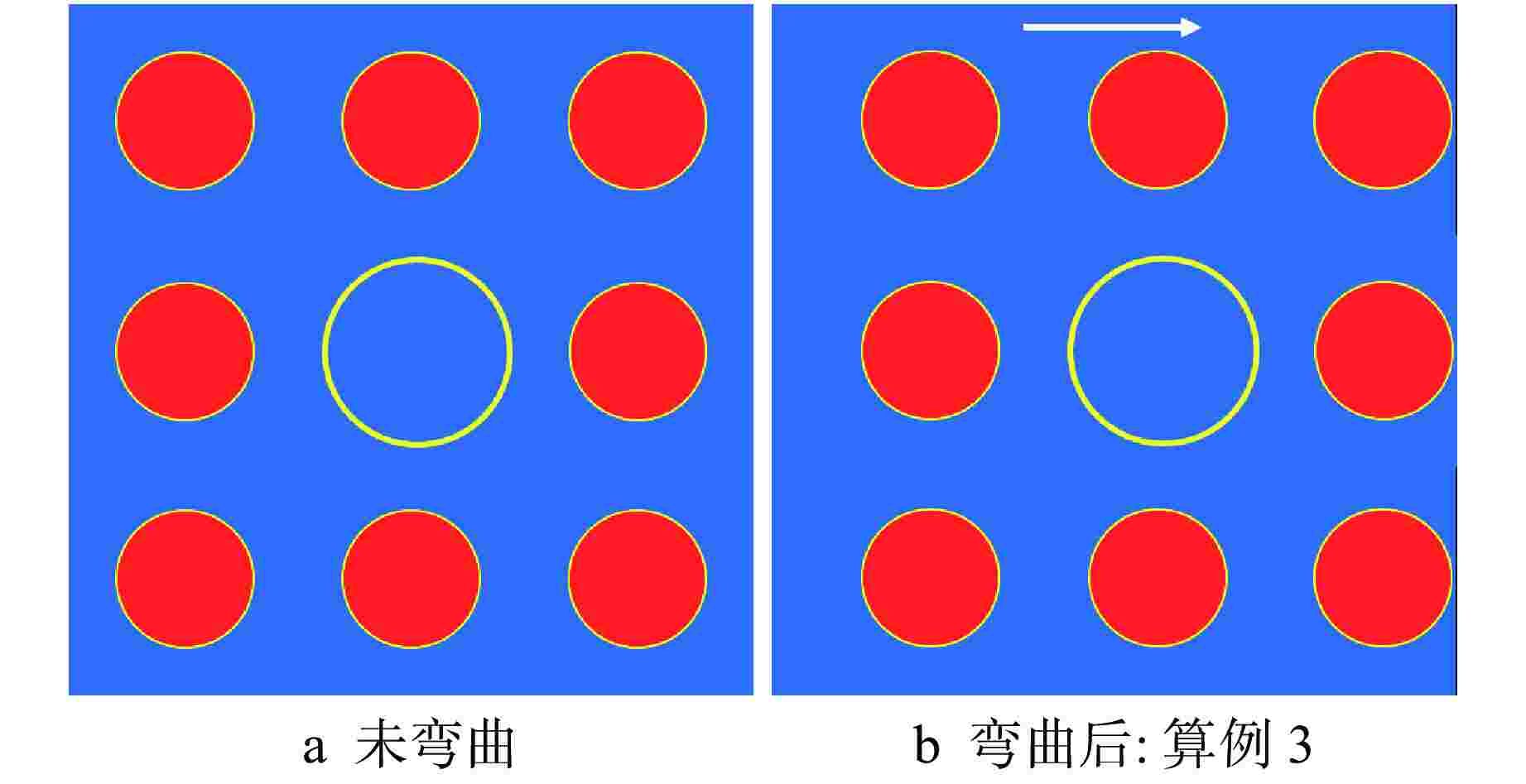
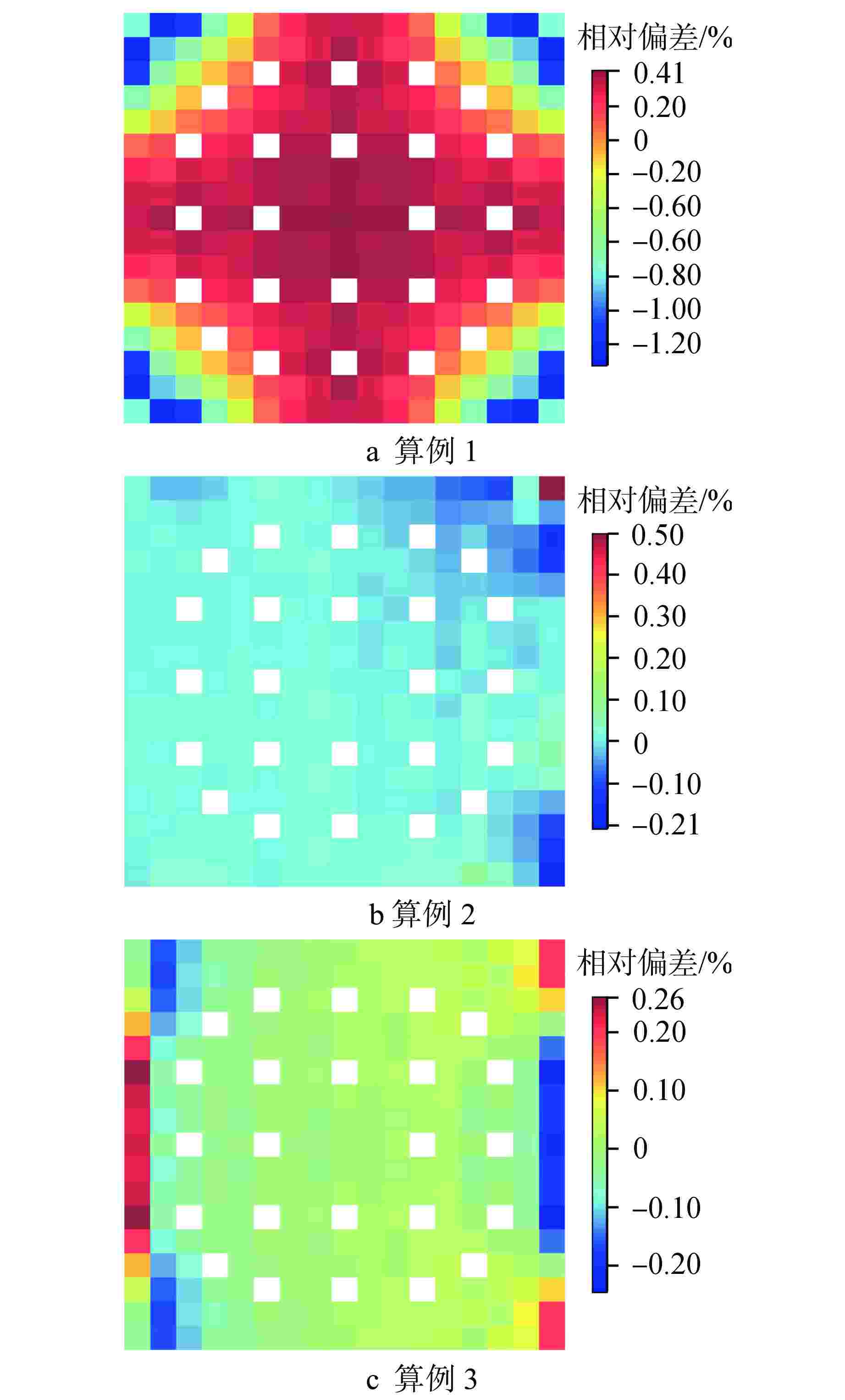
算例 程序 未弯曲模型有效增殖因数 实际建模弯曲后模型有效增殖因数 等效水隙模拟弯曲模型有效增殖因数 算例1 NECP-MCX 1.15734±0.00003 1.15051±0.00003 1.15144±0.00003 NECP-X 1.15704 1.14980 1.15088 算例2 NECP-MCX 1.15734±0.00003 1.15777±0.00003 1.15782±0.00003 NECP-X 1.15704 1.15748 1.15746 算例3 NECP-MCX 1.15734±0.00003 1.15716±0.00003 1.15701±0.00003 NECP-X 1.15660 1.15640 1.15625 
下载: 导出CSV
表 2 NECP-X与NECP-MCX程序径向功率计算偏差
Table 2. Radial Power Deviation of NECP-X and NECP-MCX
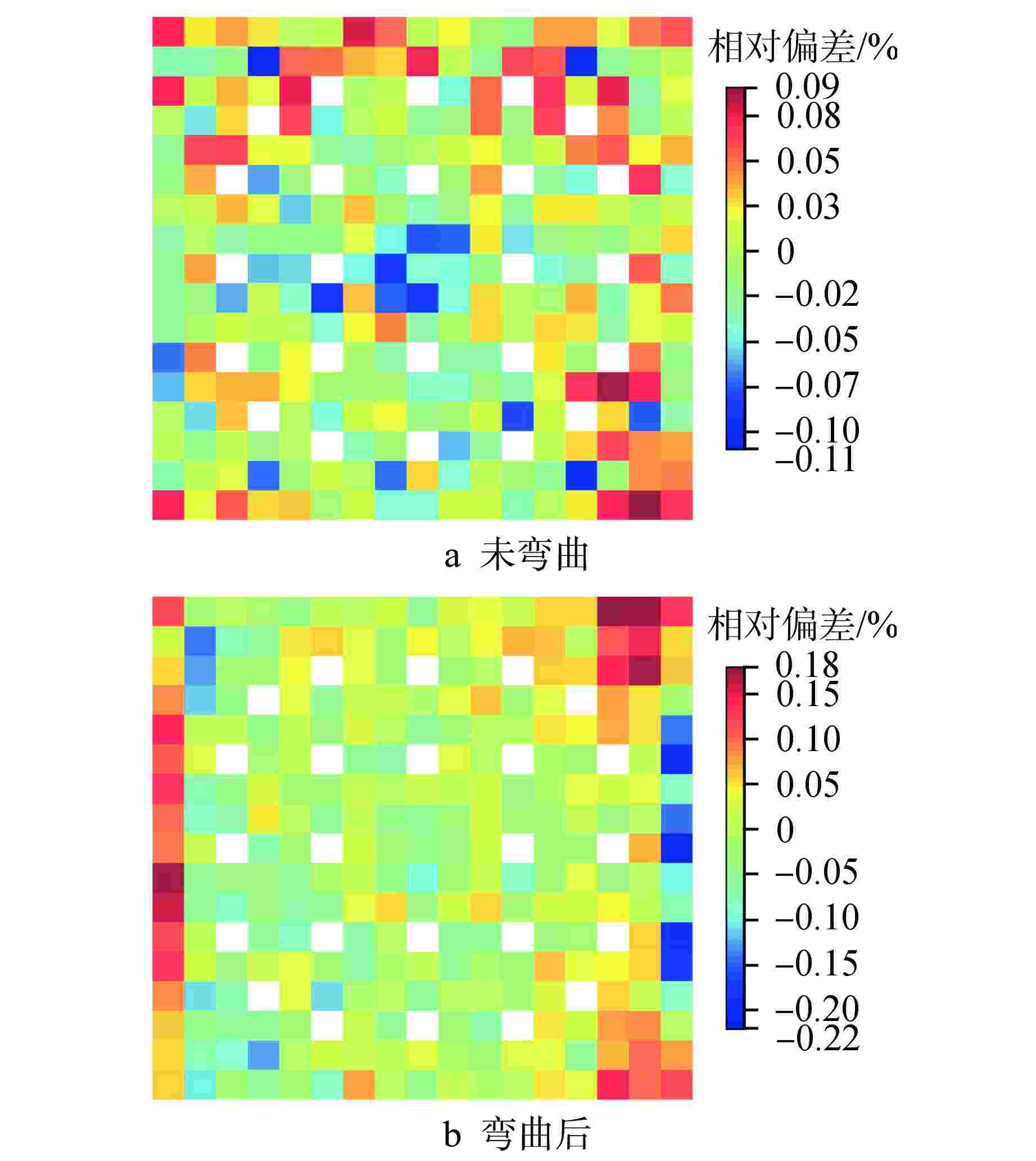
算例 NECP-X与NECP-MCX程序径向功率计算偏差/% 未弯曲模型 实际建模弯
曲后模型等效水隙模拟
弯曲模型算例1 −0.21~0.18 −0.69~0.49 −0.74~0.53 算例2 −0.21~0.18 −0.33~0.19 −0.25~0.21 算例3 −0.21~0.18 −0.21~0.31 −0.20~0.25
下载: 导出CSV
表 3 算例4有效增殖因数计算结果
Table 3. Calculation Results of Effective Multiplication Factor of Case 4
程序 未弯曲模型 弯曲后模型 弯曲前后偏差/pcm NECP-MCX 1.15349±0.00002 1.15340±0.00002 −9 NECP-X 1.15263 1.15251 −12
下载: 导出CSV
表 4 算例5有效增殖因数计算结果
Table 4. Calculation Results of Effective Multiplication Factor of Case 5
程序 未弯曲模型 实际建模弯
曲后模型等效水隙模拟
弯曲模型NECP-MCX 1.04298±0.00001 1.04313±0.00001 1.04313±0.00001 NECP-X 1.04307 — 1.04324
下载: 导出CSV
表 5 EPR全堆芯有效增殖因数计算结果
Table 5. Calculation Results of EPR Effective Multiplication Factor
算例 有效增殖因数 偏差/pcm 未弯曲 1.049419 — 弯曲 1.049838 41.9
下载: 导出CSV
-
[1] IAEA. Review of fuel failures in water cooled reactors: IAEA Nuclear Energy Series No. NF-T-2.1[R]. Vienna: IAEA, 2010. [2] DE LAMBERT S, CAMPIONI G, FAUCHER V, et al. Modeling the consequences of fuel assembly bowing on PWR core neutronics using a Monte-Carlo code[J]. Annals of Nuclear Energy, 2019, 134: 330-341. doi: 10.1016/j.anucene.2019.06.017 [3] HE Q M, ZHENG Q, LI J, et al. NECP-MCX: a hybrid Monte-Carlo-Deterministic particle-transport code for the simulation of deep-penetration problems[J]. Annals of Nuclear Energy, 2021, 151: 107978. doi: 10.1016/j.anucene.2020.107978 [4] CHEN J, LIU Z Y, ZHAO C, et al. A new high-fidelity neutronics code NECP-X[J]. Annals of Nuclear Energy, 2018, 116: 417-428. doi: 10.1016/j.anucene.2018.02.049 [5] CHEN J, ZHAO C, HE Q M, et al. Development and verifications of the high-fidelity neutronics code NECP-X[C]. Chengdu: Reactor Physics Asia, 2017. [6] LIU Z Y, HE Q M, ZU T J, et al. The pseudo-resonant-nuclide subgroup method based global-local self-shielding calculation scheme[J]. Journal of Nuclear Science and Technology, 2018, 55(2): 217-228. doi: 10.1080/00223131.2017.1394232 [7] LIU Z Y, HE Q M, WEN X J, et al. Improvement and optimization of the pseudo-resonant-nuclide subgroup method in NECP-X[J]. Progress in Nuclear Energy, 2018, 103: 60-73. doi: 10.1016/j.pnucene.2017.11.006 [8] ZHAO C, LIU Z Y, MA D W, et al. The iteration and parallel strategy for the 2D/1D transport method in NECP-X[C]//International Conference on Mathematics & Computational Methods Applied to Nuclear Science & Engineering. Jeju, Korea: Korean Nuclear Society, 2017. [9] ZU T J, XU J L, TANG Y Q, et al. NECP-Atlas: a new nuclear data processing code[J]. Annals of Nuclear Energy, 2019, 123: 153-161. doi: 10.1016/j.anucene.2018.09.016 -
计量
- 文章访问数: 381
- HTML全文浏览量: 25
- PDF下载量: 50
- 被引次数: 0
