曲网格下的厚扩散极限中子输运模拟研究

王新宇; 张斌; 陈义学

doi:10.13832/j.jnpe.2023.04.0041

曲网格下的厚扩散极限中子输运模拟研究

doi: 10.13832/j.jnpe.2023.04.0041

华北电力大学核科学与工程学院，北京，102206

基金项目: 国家自然科学基金(11975097)

详细信息

作者简介:
王新宇（1990—），男，博士研究生，现主要从事粒子输运数值计算方法研究，E-mail: wangxy@ncepu.edu.cn

通讯作者:
张　斌，E-mail: zhangbin@ncepu.edu.cn

中图分类号: TL328
计量
- 文章访问数: 141
- HTML全文浏览量: 22
- PDF下载量: 25
- 被引次数: 0
出版历程
- 收稿日期: 2022-10-08
- 修回日期: 2022-11-26
- 刊出日期: 2023-08-15

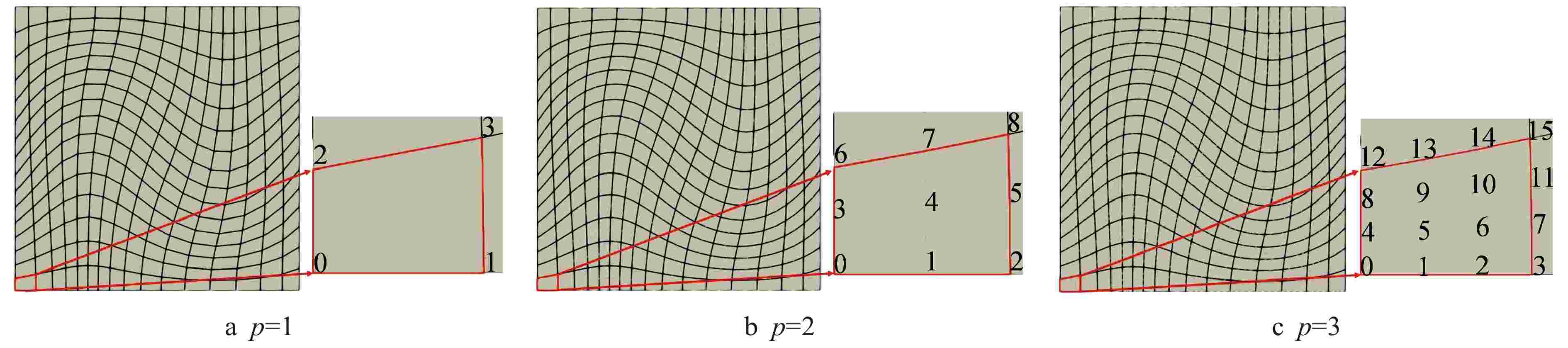
Research on Simulation of Neutron Transport with Thick Diffusion Limit in Curved Meshes

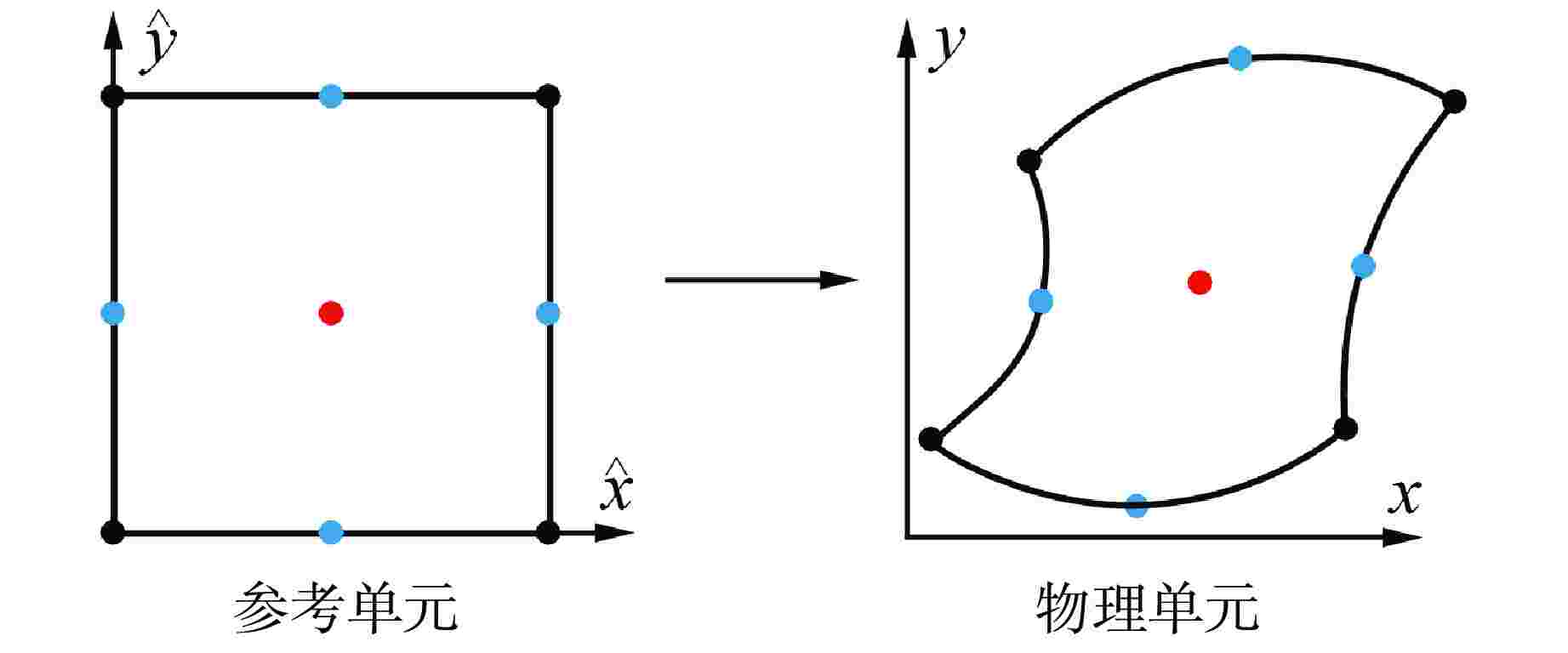
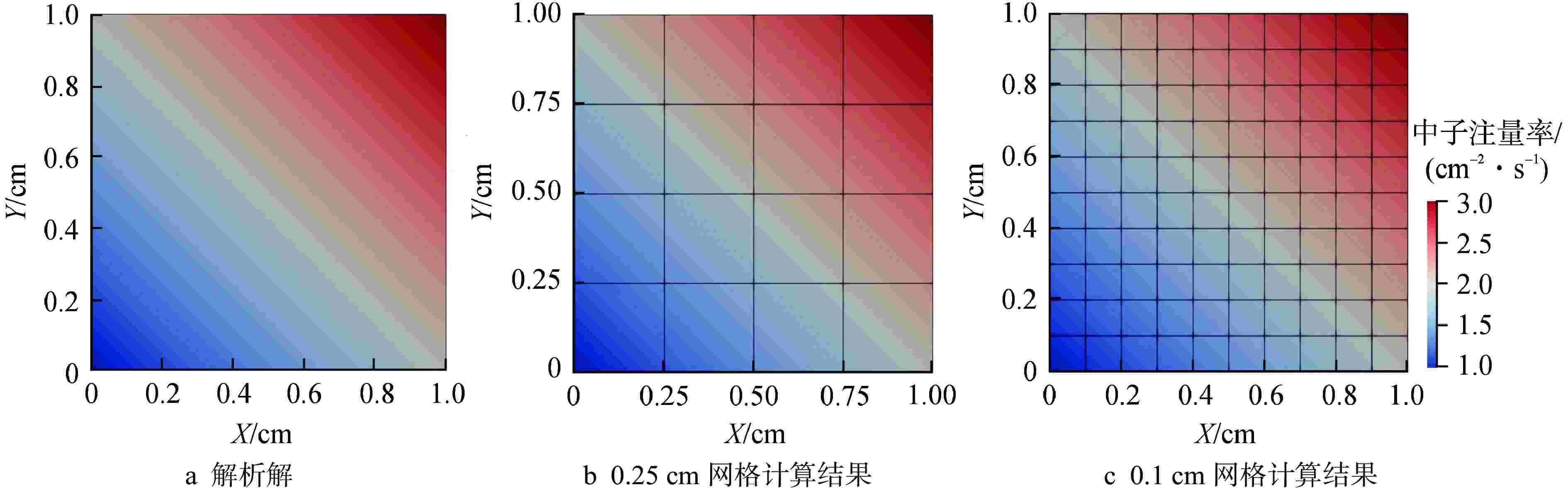
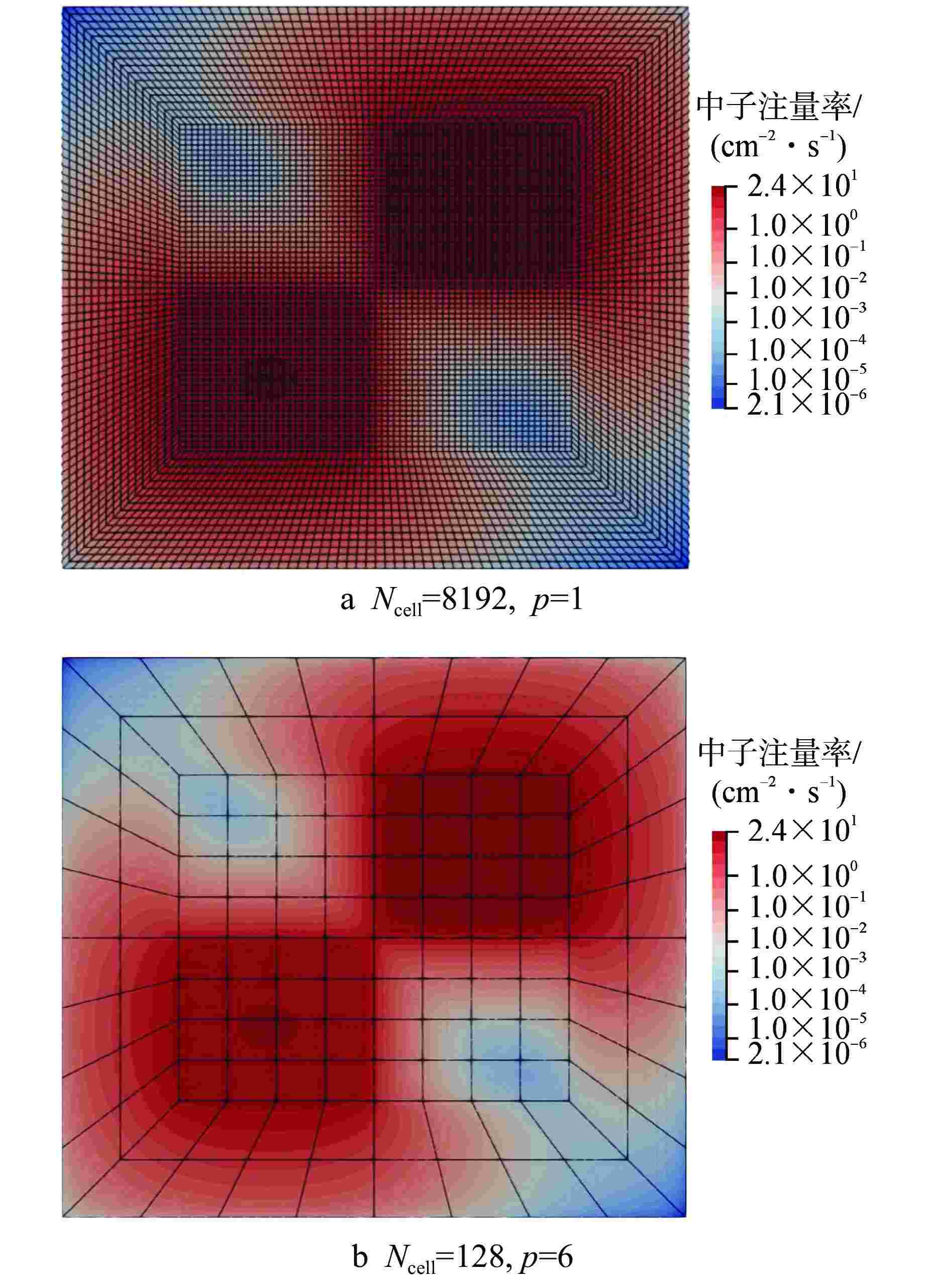
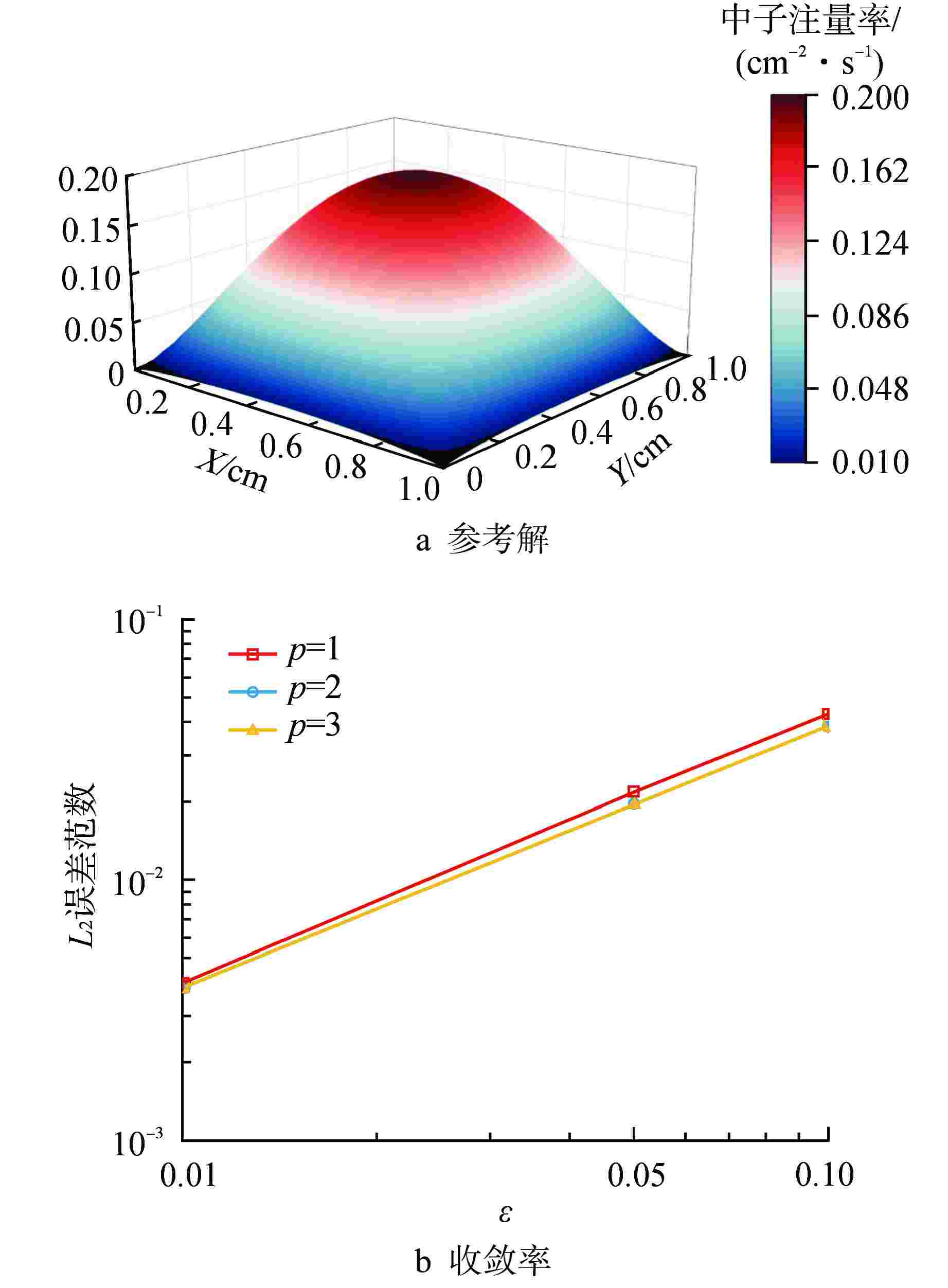
School of Nuclear Science and Engineering, North China Electric Power University, Beijing, 102206, China

摘要

摘要: 离散纵标法作为求解厚扩散极限中子输运问题的重要方法之一，其常用的空间离散格式，如有限差分格式极易在光学厚介质中产生数值扩散，并且粗网格精度不足和难以适配复杂几何等问题使得离散纵标法的应用具有一定的局限性。本研究采用伽辽金方法推导弱形式或变分形式的离散纵标方程，基于间断有限元思想构造高阶曲网格下的拉格朗日有限元基函数，建立中子输运方程的高阶间断有限元离散格式。选取了构造解算例、国际原子能机构（IAEA） EIR-2基准题和厚扩散极限算例进行建模与输运计算，对该空间离散格式的计算精度、收敛性进行了测试验证并分析了其厚扩散极限特性。数值结果表明，多介质问题中高阶间断有限元格式的计算结果与基准值相对误差小于1%，且在曲网格下也具有较高的计算精度和符合预期的收敛速度。该离散格式可有效解决曲网格下的厚扩散极限中子输运问题，具有较好的数值特性，且在光学厚扩散极限下具备扩散极限渐近保持性质。
- 中子输运 /
- 离散纵标法 /
- 空间离散格式 /
- 间断有限元 /
- 厚扩散极限
Abstract: Discrete ordinate method is one of the main numerical methods for solving the problem of neutron transport with thick diffusion limit. Its commonly used spatial discrete schemes, such as finite difference scheme, are easy to cause numerical diffusion in optical thick media, and the application of discrete ordinate method has certain limitations due to the lack of coarse mesh accuracy and difficulty in adapting to complex geometry. In this paper, Galerkin method is used to derive discrete ordinate equations in weak form or variational form. Based on the idea of discontinuous finite element, the Lagrangian finite element basis function in the higher-order curved meshes is constructed to establish the higher-order finite element discrete scheme of the transport equation. Two manufactured solution examples, the IAEA EIR-2 benchmark problem and the thick diffusion limit example, are selected for modeling and transport calculation, and the calculation accuracy and convergence of the spatial discrete scheme are tested and verified, and its thick diffusion limit characteristics are analyzed. The numerical results show that the relative error between the calculated results of high-order discontinuous finite element scheme and the reference value is less than 1%, and it also has high calculation accuracy and convergence rate in curved meshes. The discrete scheme can effectively solve the problem of neutron transport with thick diffusion limit in curved meshes. It has good numerical characteristics, and has the asymptotic preservation property of diffusion limit under optical thick diffusion limit.
- Neutron transport /
- Discrete ordinate method /
- Spatial discretization /
- Discontinuous finite element /
- Thick diffusion limit

HTML全文

图 1 四边形单元的自由度示意图

p—阶数

Figure 1. Degree of Freedom of Quadrilateral Element

下载: 全尺寸图片幻灯片

图 2 从参考单元到物理单元的双二次仿射映射

Figure 2. Biquadraticr Affine Mapping from Reference Element to Physical Element

下载: 全尺寸图片幻灯片

图 3 MMS-1模型构造解和计算结果示意图

Figure 3. Manufactured Solution and Results of MMS-1 Model

下载: 全尺寸图片幻灯片

图 4 IAEA EIR-2基准题的几何和材料示意图

Figure 4. Geometry and Material Properties of IAEA EIR-2 Benchmark Problem

下载: 全尺寸图片幻灯片

图 5 IAEA EIR-2基准题的网格剖分和中子注量率分布

Figure 5. Mesh Generation and Neutron Flux Distribution of IAEA EIR-2 Benchmark Problem

下载: 全尺寸图片幻灯片

图 6 MMS-2模型构造解示意图

Figure 6. Manufactured Solution of MMS-2 Model

下载: 全尺寸图片幻灯片

图 7 MMS-2算例的网格剖分

Figure 7. Mesh Generation of MMS-2 Example

下载: 全尺寸图片幻灯片

图 8 MMS-2模型的收敛性

Figure 8. Convergence of MMS-2 Model

下载: 全尺寸图片幻灯片

图 9 厚扩散极限问题的参考解及收敛率

Figure 9. Reference Solution and Convergence Rate of Thick Diffusion Limit Problem

下载: 全尺寸图片幻灯片

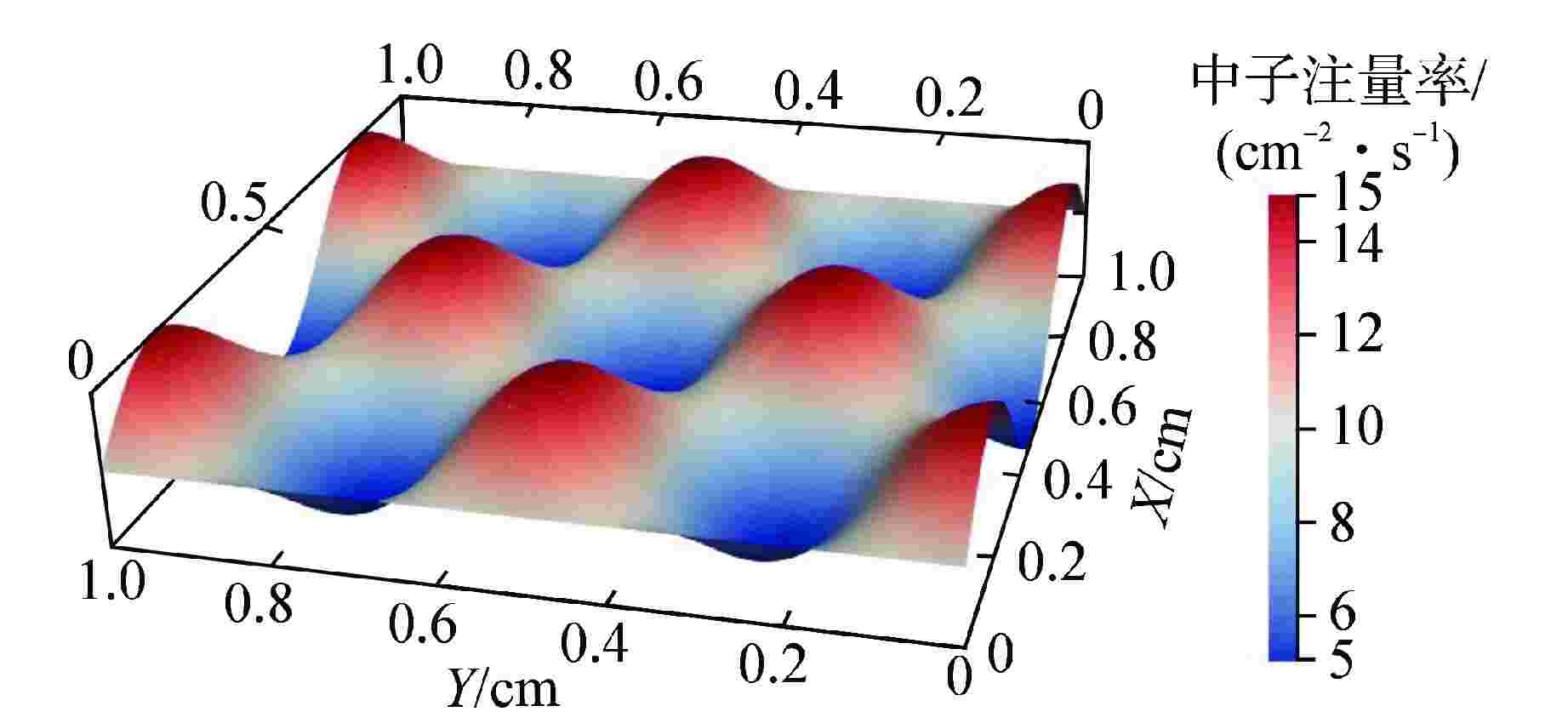
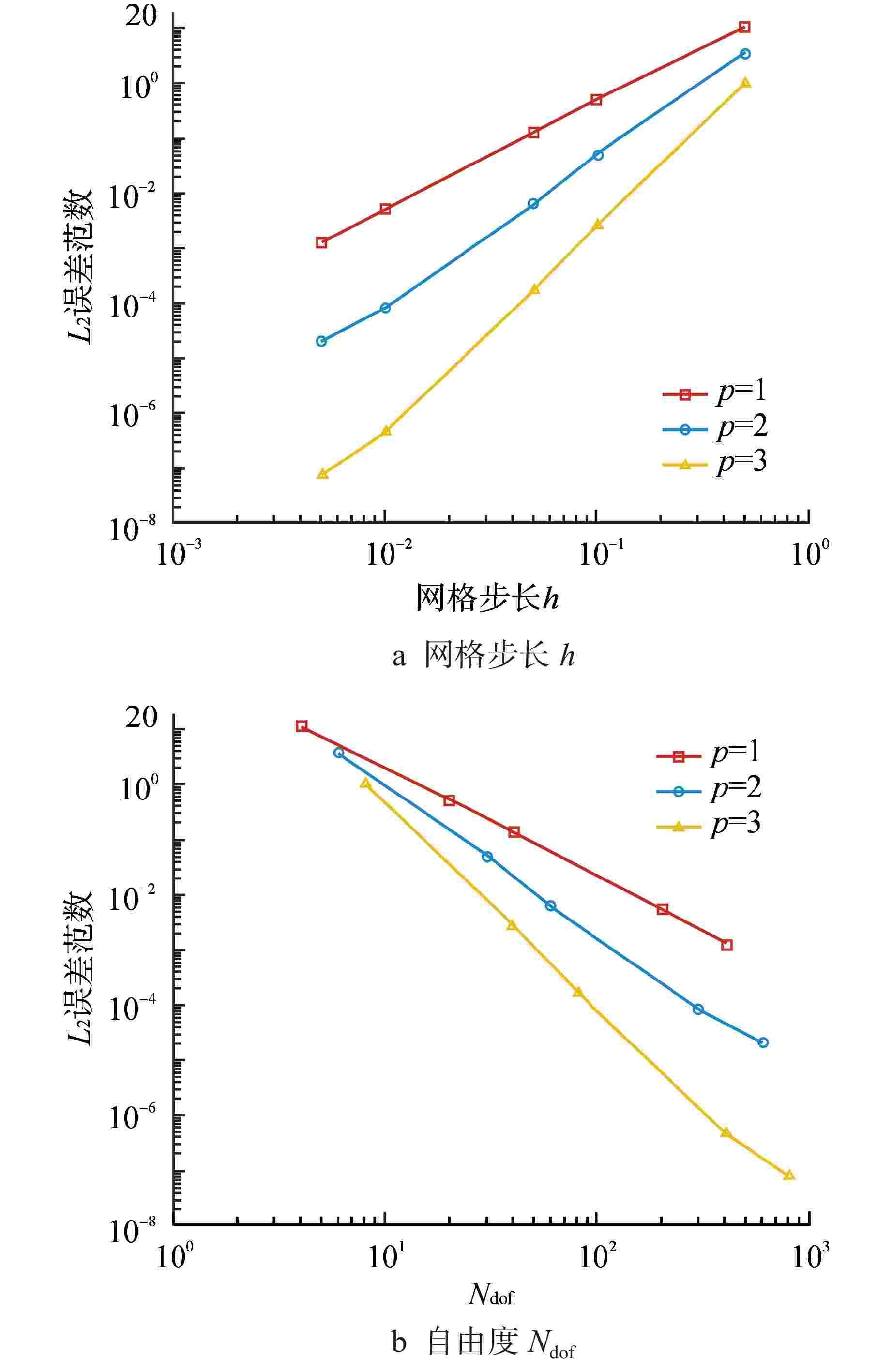
表 1 0.1 cm网格步长下1~4阶有限元的L₂误差范数

Table 1. L₂-norm of Error of 1st-4th Order Finite Element with 0.1 cm Mesh Spacing

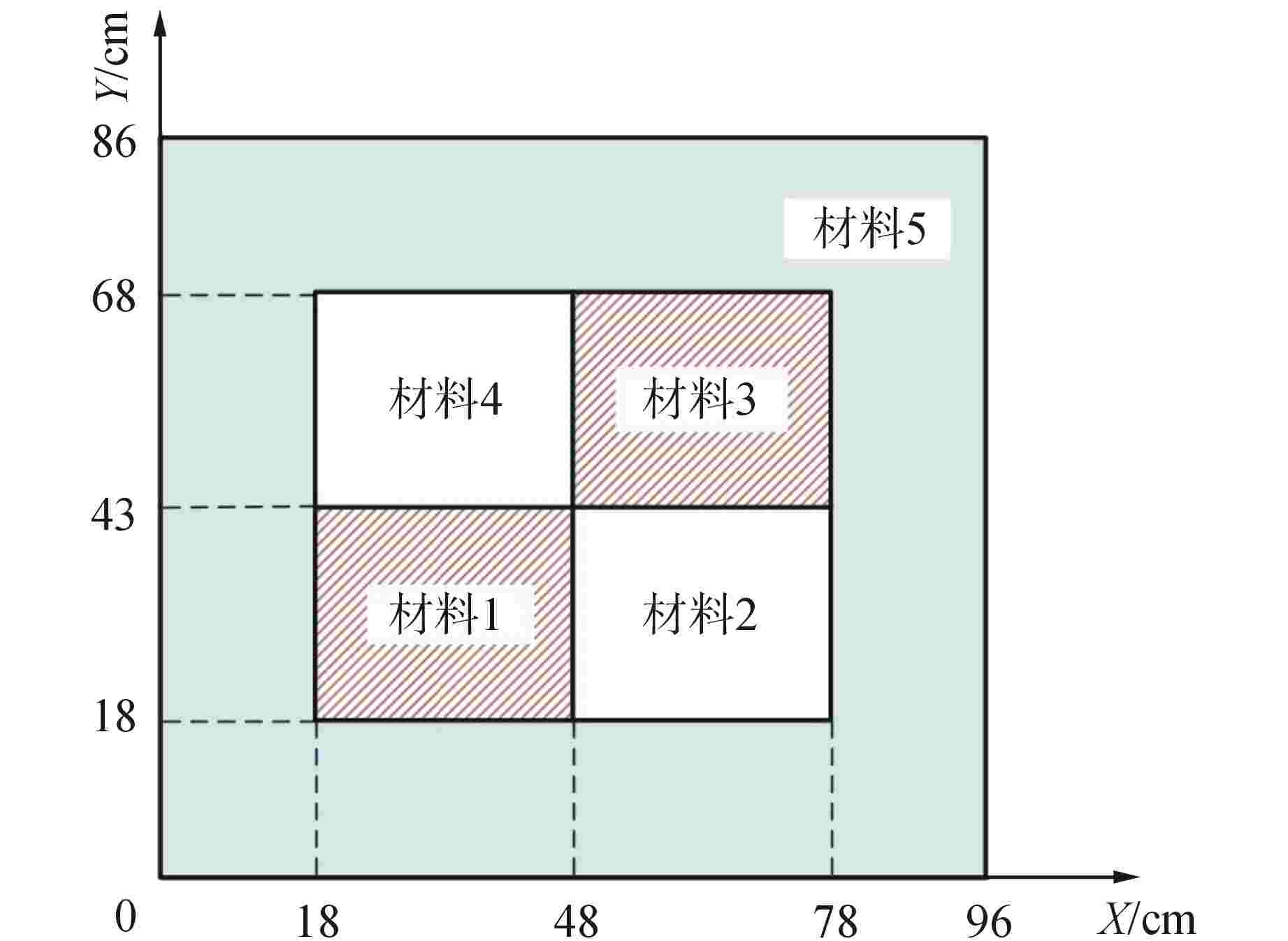
p	1	2	3	4
L₂	4.9838×10⁻¹²	2.7034×10⁻¹¹	3.8589×10⁻¹¹	1.7194×10⁻¹¹

下载: 导出CSV

表 2 IAEA EIR-2基准题的截面与源强

Table 2. Cross Section and Source Strength of IAEA EIR-2 Benchmark Problem

材料编号	中子源强/(cm⁻³·s⁻¹)	σ_t/cm⁻¹	σ_s/cm⁻¹
1	1.0	0.60	0.53
2	0.0	0.48	0.20
3	1.0	0.70	0.66
4	0.0	0.65	0.50
5	0.0	0.90	0.89

下载: 导出CSV

表 3 IAEA EIR-2基准题的计算结果

Table 3. Results for IAEA EIR-2 Benchmark Problem

材料编号	区域平均中子注量率/(cm⁻²·s⁻¹)
材料编号	参考解	LDFE	HDFE
1	1.1960×10¹	1.1951×10¹	1.1954×10¹
2	5.3968×10⁻¹	5.4222×10⁻¹	5.4153×10⁻¹
3	1.9202×10¹	1.9185×10¹	1.9191×10¹
4	8.3364×10⁻¹	8.3671×10⁻¹	8.3551×10⁻¹
5	1.5263×10⁰	1.5375×10⁰	1.5274×10⁰

下载: 导出CSV

参考文献(20)

[1]	GRAZIANI F. Computational methods in transport[M]. New York: Springer, 2004: 527-530.
[2]	ATZENI S, MEYER-TER-VEHN J. 惯性聚变物理[M]. 沈百飞, 译. 北京: 科学出版社, 2008: 162-196.
[3]	LEWIS E E, MILLER W F JR. Computational methods of neutron transport[M]. La Grange Park: American Nuclear Society, 1993: 116-153.
[4]	LATHROP K D. Spatial differencing of the transport equation: positivity vs. accuracy[J]. Journal of Computational Physics, 1969, 4(4): 475-498. doi: 10.1016/0021-9991(69)90015-1
[5]	PETROVIC B, HAGHIGHAT A. New directional theta-weighted S_N differencing scheme and its application to pressure vessel fluence calculations[C]//Proceedings of Radiation Protection and Shielding Topical Meeting. Falmouth, 1996: 3-10.
[6]	LARSEN E W, ALCOUFFE R E. Linear characteristic method for spatially discretizing the discrete ordinates equations in (X, Y)-geometry: LA-UR-81-101[R]. Los Alamos: Los Alamos Scientific Laboratory, 1981.
[7]	AZMY Y Y. Arbitrarily high order characteristic methods for solving the neutron transport equation[J]. Annals of National Energy, 1992, 19(10-12): 593-606. doi: 10.1016/0306-4549(92)90004-U
[8]	REED W H, HILL T R. Triangular mesh methods for the neutron transport equation: LA-UR-73-479[R]. Los Alamos: Los Alamos Scientific Laboratory, 1973.
[9]	MOREL J E, DENDY J E JR, WAREING T A. Diffusion-accelerated solution of the two-dimensional S_n equations with bilinear-discontinuous differencing[J]. Nuclear Science and Engineering, 1993, 115(4): 304-319. doi: 10.13182/NSE93-A24061
[10]	MOREL J E, WAREING T A, SMITH K. A linear-discontinuous spatial differencing scheme for S_n radiative transfer calculations[J]. Journal of Computational Physics, 1996, 128(2): 445-462. doi: 10.1006/jcph.1996.0223
[11]	WANG Y Q, RAGUSA J C. A high-order discontinuous Galerkin method for the S_N transport equations on 2D unstructured triangular meshes[J]. Annals of Nuclear Energy, 2009, 36(7): 931-939. doi: 10.1016/j.anucene.2009.03.002
[12]	WANG Y Q, RAGUSA J C. On the convergence of DGFEM applied to the discrete ordinates transport equation for structured and unstructured triangular meshes[J]. Nuclear Science and Engineering, 2009, 163(1): 56-72. doi: 10.13182/NSE08-72
[13]	WANG Y Q, RAGUSA J C. Standard and goal-oriented adaptive mesh refinement applied to radiation transport on 2D unstructured triangular meshes[J]. Journal of Computational Physics, 2011, 230(3): 763-788. doi: 10.1016/j.jcp.2010.10.018
[14]	HACKEMACK M W, RAGUSA J C. Quadratic serendipity discontinuous finite element discretization for S_N transport on arbitrary polygonal grids[J]. Journal of Computational Physics, 2018, 374: 188-212. doi: 10.1016/j.jcp.2018.05.032
[15]	洪振英,袁光伟,魏军侠. 球几何中子输运保正线性间断有限元格式[J]. 强激光与粒子束,2017, 29(7): 076001. doi: 10.11884/HPLPB201729.160320
[16]	LARSEN E W, MOREL J E, MILLER W F. Asymptotic solutions of numerical transport problems in optically thick, diffusive regimes[J]. Journal of Computational Physics, 1987, 69(2): 283-324. doi: 10.1016/0021-9991(87)90170-7
[17]	CHEN Y X, ZHANG B, ZHANG L, et al. ARES: a parallel discrete ordinates transport code for radiation shielding applications and reactor physics analysis[J]. Science and Technology of Nuclear Installations, 2017, 2017: 2596727.
[18]	ANDERSON R, ANDREJ J, BARKER A, et al. MFEM: a modular finite element methods library[J]. Computers & Mathematics with Applications, 2021, 81: 42-74.
[19]	SCHUNERT S, AZMY Y. Comparison of spatial discretization methods for solving the S_N equations using a three-dimensional method of manufactured solutions benchmark suite with escalating order of nonsmoothness[J]. Nuclear Science and Engineering, 2015, 180(1): 1-29. doi: 10.13182/NSE14-77
[20]	KAVENOKY, STEPANEK J, SCHMIDT F. Transport theory and advanced reactor calculations: IAEA-TECDOC-254[R]. Vienna: International Atomic Energy Agency, 1981.