Research on Automatic Modeling Method of TORT Program Based on CAD Model
-
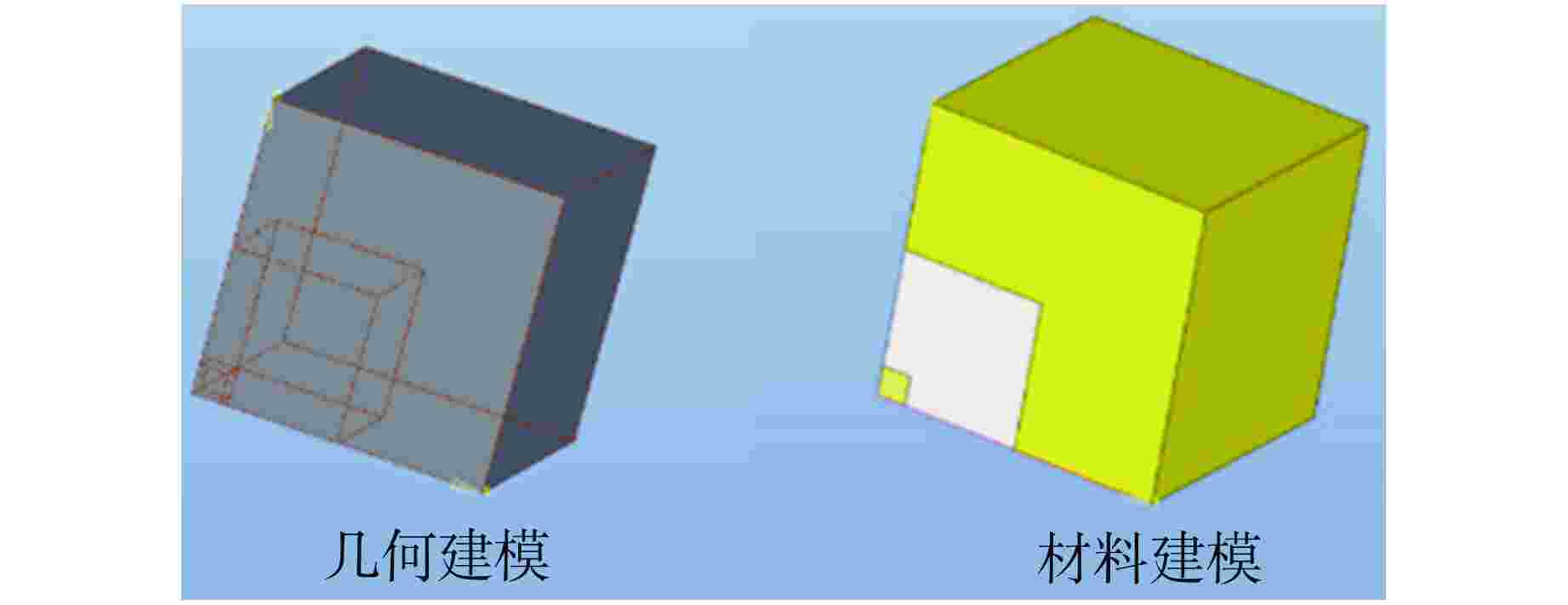
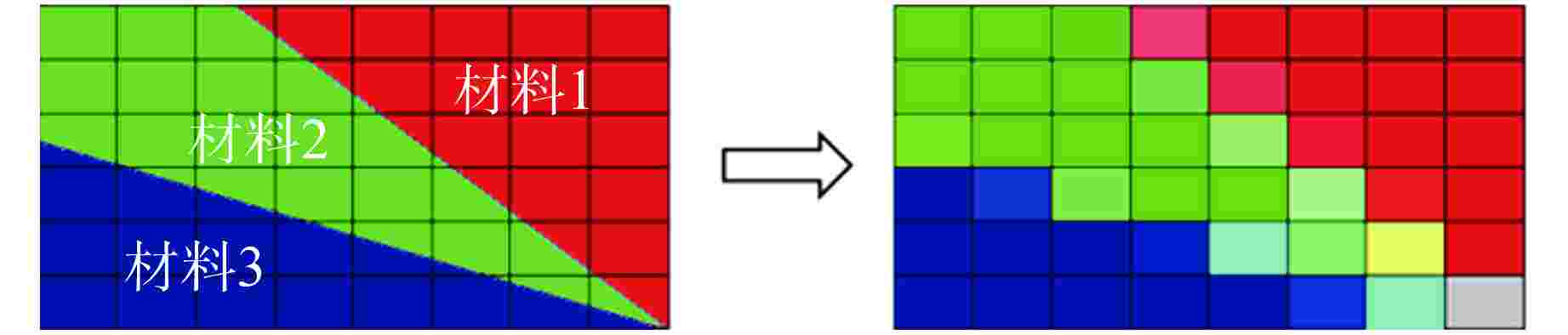
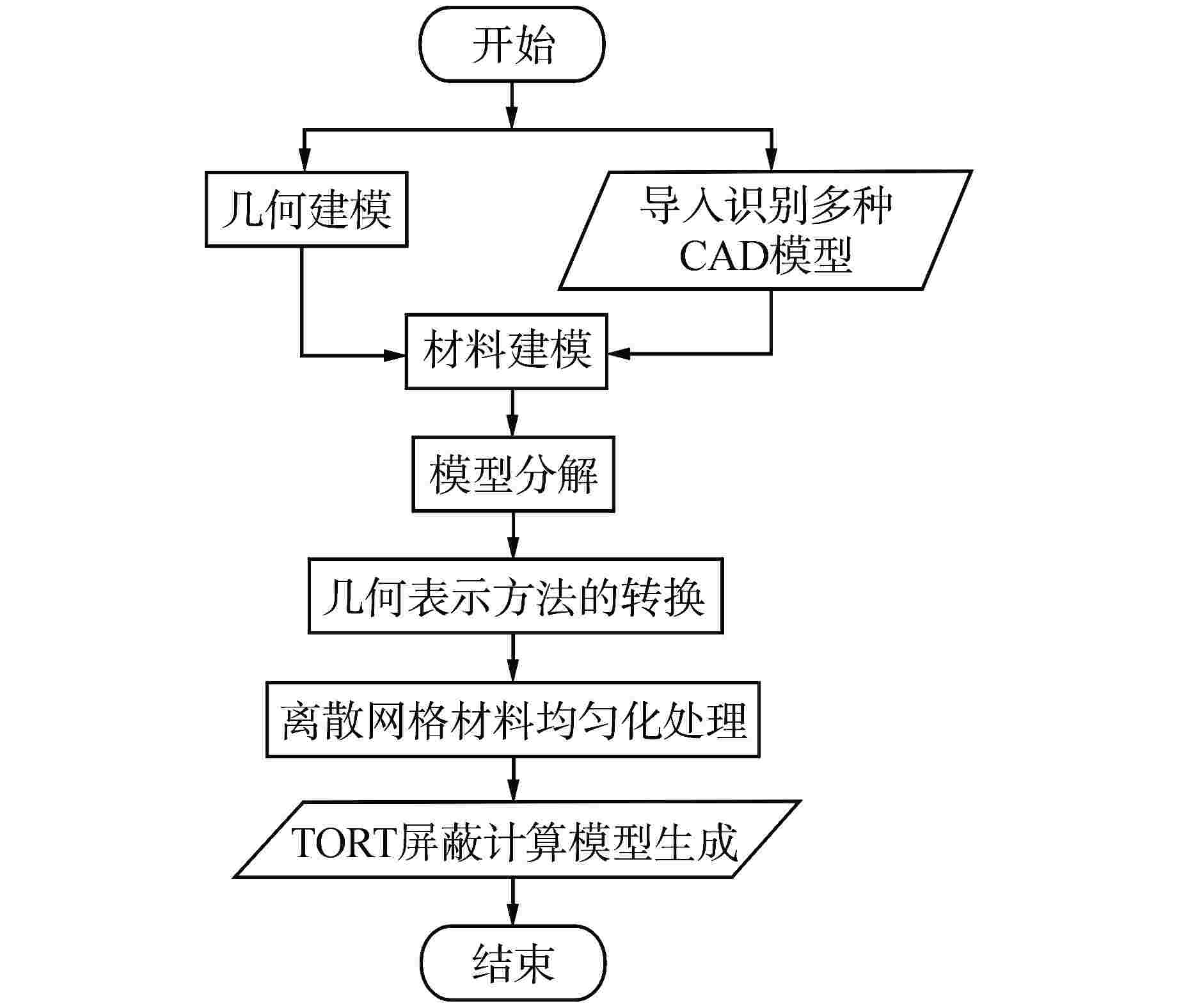
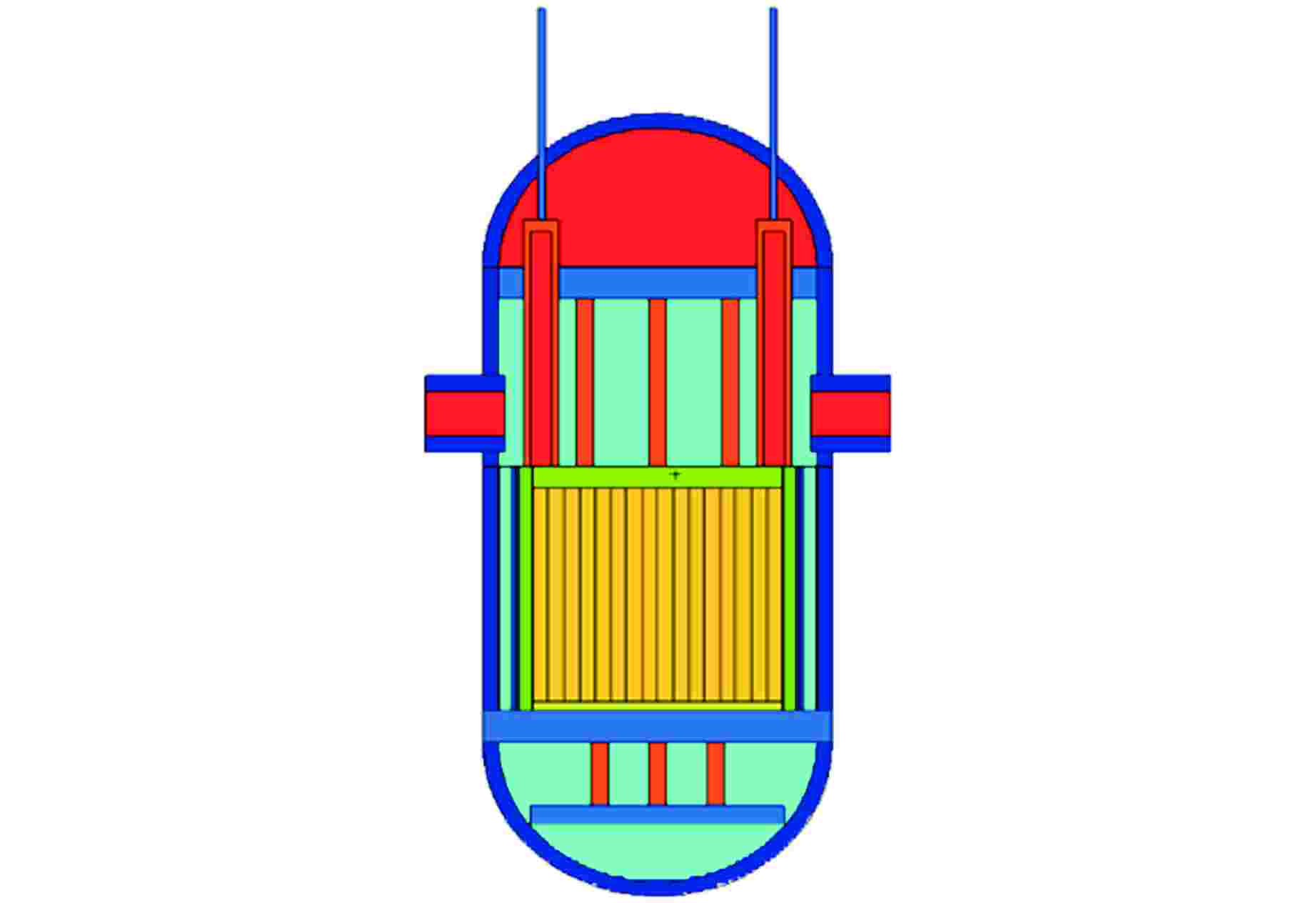
摘要: 针对反应堆屏蔽结构几何复杂，传统手动建模几何处理能力有限、效率低、易于出错的问题，基于多功能辐射输运模拟仿真平台（MOSRT），采用离散网格材料体积权重均匀化方法对多材料的离散网格进行均匀化处理，实现了CAD模型到三维离散纵标法（SN）计算程序TORT屏蔽计算模型的精细转换。基于Kobayashi和NUREG-CR-6115基准题模型对自动建模方法进行了验证。结果表明，对于Kobayashi基准题，自动建模方法与手动建模结果完全吻合；对于NUREG-CR-6115基准题，自动建模方法与参考解的最大误差为12.2%。该验证结果表明了自动建模方法的有效性与正确性。Abstract: Aiming at the problems of complex geometry of reactor shielding structure, limited geometric processing ability, low efficiency and error prone of traditional manual modeling, based on the multi-objective modeling and simulation platform for radiation transport (MOSRT), the volume weight homogenization method of discrete mesh materials is used to homogenize the discrete meshes of multi-materials, and the fine transformation from CAD model to three-dimensional discrete ordinate method (SN) calculation program TORT shielding calculation model is realized. Based on the Kobayashi and NUREG-CR-6115 benchmark models, the automatic modeling method is verified. The results show that for the Kobayashi benchmark problem, the automatic modeling method is completely consistent with the manual modeling results. For the NUREG-CR-6115 benchmark problem, the maximum error between the automatic modeling method and the reference solution is 12.2%. The verification results show the effectiveness and correctness of the automatic modeling method.
-
图 8 压力容器处的中子通量密度与参考解的比较(E>1.0 MeV)
Figure 8. Comparison of Neutron Flux Density in Pressure Vessel with Reference Solution (E>1.0 MeV)
图 9 压力容器处的中子通量密度相对误差
Figure 9. Relative Error of Neutron Flux Density in Pressure Vassel
表 1 Kobayashi计算结果与手动建模的比较
Table 1. Comparison of Kobayashi Calculation Results with Manual Modeling
离散网格中心点坐标
/cm中子通量密度/(cm−2·s−1) 相对误差
/%手动建模 自动建模 (5,5,5) 5.9650×100 5.9650×100 0 (15,15,15) 4.3160×10−1 4.3160×10−1 0 (25,25,25) 1.8748×10−1 1.8748×10−1 0 (35,35,35) 7.0853×10−2 7.0853×10−2 0 (45,45,45) 4.6453×10−2 4.6453×10−2 0 (55,55,55) 1.4268×10−2 1.4268×10−2 0 (65,65,65) 1.9167×10−3 1.9167×10−3 0 (75,75,75) 2.3910×10−4 2.3910×10−1 0 (85,85,85) 2.9276×10−5 2.9276×10−1 0 (95,95,95) 3.5710×10−6 3.5710×10−6 0 
下载: 导出CSV
表 2 2种离散网格材料填充方法的计算结果与手动建模的比较
Table 2. Comparison of Calculation Results of Two Discrete Mesh Material Filling Methods with Manual Modeling
离散网格中心点坐标/cm 中子通量密度/(cm−2·s−1) 相对误差/% 手动建模 自动建模中心点方法 自动建模均匀化方法 自动建模中心点方法 自动建模均匀化方法 (5,5,5) 5.96498×100 5.96498×10−0 5.9650×100 0 0 (15,15,15) 4.31603×10−1 4.31603×10−1 4.3160×10−1 0 0 (25,25,25) 1.87480×10−1 1.87480×10−1 1.8748×10−1 0 0 (35,35,35) 7.08528×10−2 7.08529×10−2 7.0853×10−2 0 0 (45,45,45) 4.64533×10−2 4.64534×10−2 4.6453×10−2 0 0 (55,55,55) 1.42682×10−2 1.37339×10−2 1.4098×10−2 3.74 1.19 (65,65,65) 1.91668×10−3 1.84493×10−3 1.8997×10−3 3.74 0.89 (75,75,75) 2.39097×10−4 2.30865×10−4 2.3781×10−4 3.44 0.54 (85,85,85) 2.92763×10−5 2.80120×10−5 2.8838×10−5 4.32 1.50 (95,95,95) 3.57102×10−6 3.37525×10−6 3.5077×10−6 5.48 1.77
下载: 导出CSV
-
[1] DOICU A, MISHCHENKO M I, EFREMENKO D S, et al. Spectral spherical harmonics discrete ordinate method[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2021, 258: 107386. doi: 10.1016/j.jqsrt.2020.107386 [2] 应栋川,谭怡,肖锋,等. 三维离散纵标方法在反应堆精细屏蔽计算中的应用研究[J]. 核科学与工程,2017, 37(5): 756-760. doi: 10.3969/j.issn.0258-0918.2017.05.008 [3] WANG M K, TAUTGES T J, HENDERSON D L, et al. Three-dimensional modeling of complex fusion devices using CAD-MCNPX interface[J]. Fusion Science and Technology, 2005, 47(4): 1079-1083. doi: 10.13182/FST05-A830 [4] ORSI, R. BOT3P: bologna radiation transport analysis pre-post-processors version 4.0[J]. Nuclear Science & Engineering the Journal of the American Nuclear Society, 2005, 150(3):368-373. [5] 刘嘉嘉,田超,肖锋,等. MCNP-TORT屏蔽校核高保真几何转换方法研究[J]. 核动力工程,2019, 40(S2): 117-120. doi: 10.13832/j.jnpe.2019.S2.0117 [6] YANG C, CHENG T P, DENG L, et al. Development of 3-D parallel first-collision source method for discrete ordinate code JSNT-S[J]. Annals of Nuclear Energy, 2020, 135: 106942. doi: 10.1016/j.anucene.2019.106942 [7] 胡海敏,李静惊,李莹,等. SN方法粒子输运计算程序自动建模关键技术问题研究[J]. 原子核物理评论,2006, 23(2): 134-137. doi: 10.3969/j.issn.1007-4627.2006.02.011 [8] 王鑫. 实体模型边界表示向构造实体几何表示转换方法研究[D]. 北京: 清华大学, 2013. [9] KOBAYASHI K, SUGIMURA N, NAGAYA Y. 3D radiation transport benchmark problems and results for simple geometries with void region[J]. Progress in Nuclear Energy, 2001, 39(2): 119-144. doi: 10.1016/S0149-1970(01)00007-5 [10] CAREW J F. PWR and BWR pressure vessel fluence calculation benchmark problems and solutions[M]. Washington: Division of Engineering Technology, Office of Nuclear Regulatory Research, US Nuclear Regulatory Commission, 2001: 1-278. -
计量
- 文章访问数: 184
- HTML全文浏览量: 42
- PDF下载量: 33
- 被引次数: 0
