Derivation and Evaluation of Carbon Dioxide Partial Derivative Property by Implicit Solution of Brayton Cycle System
-
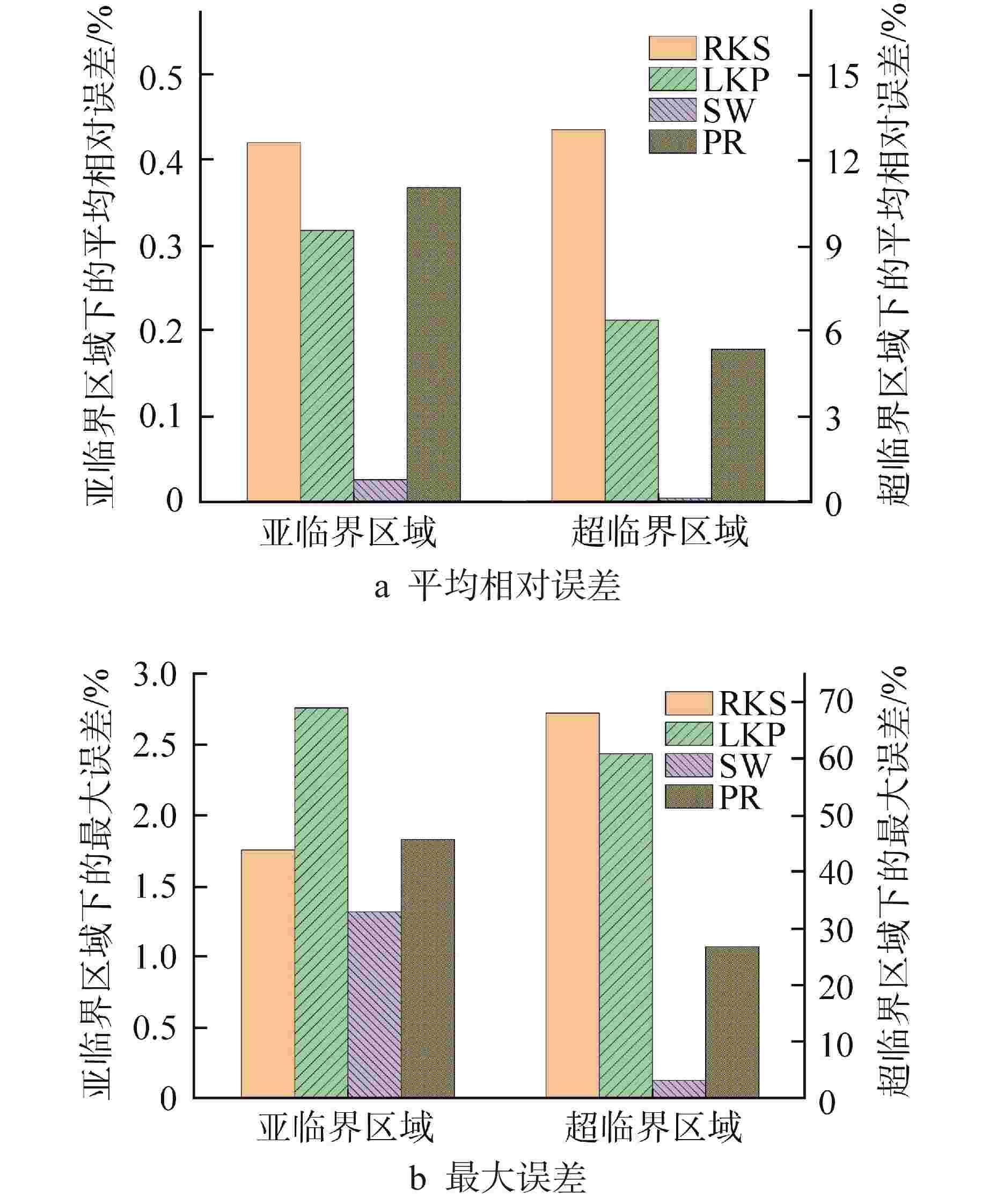
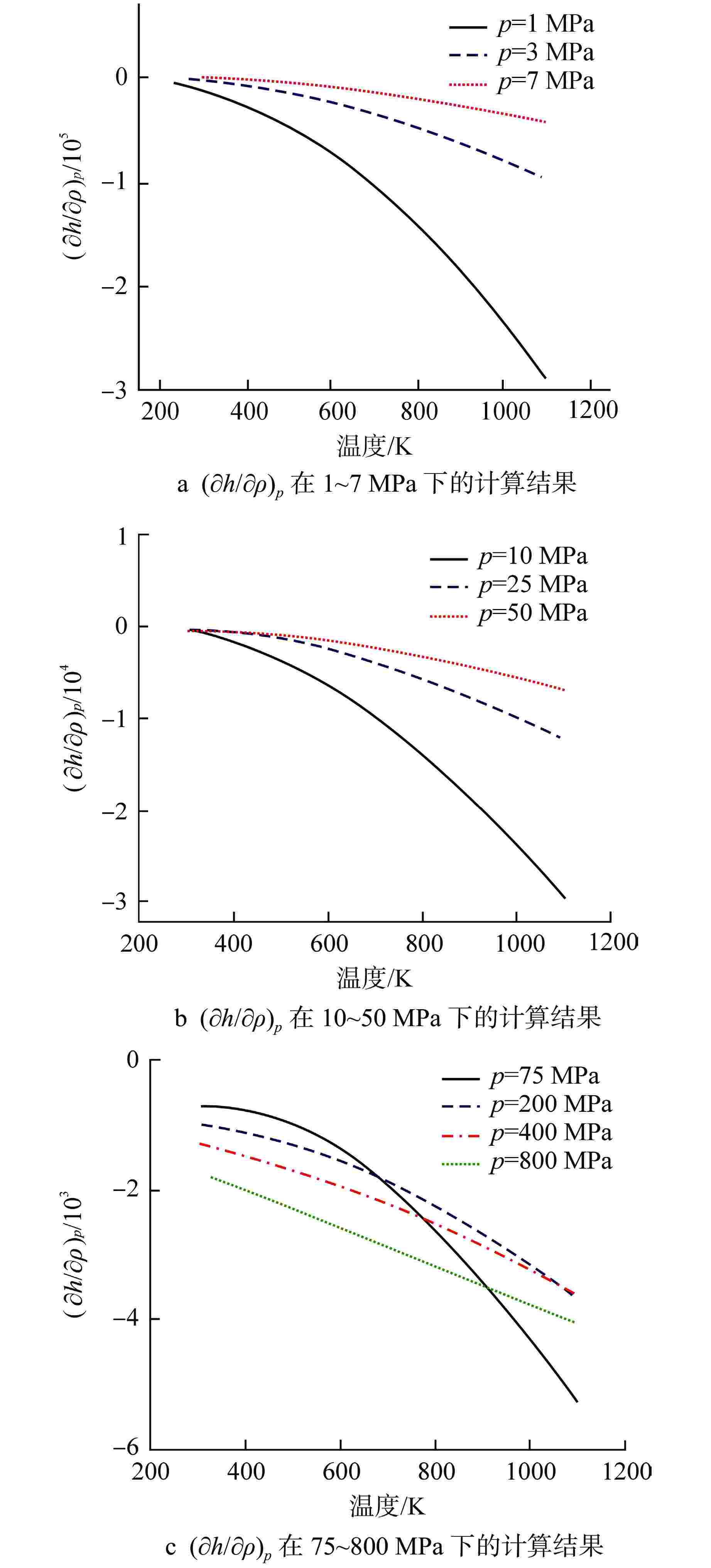
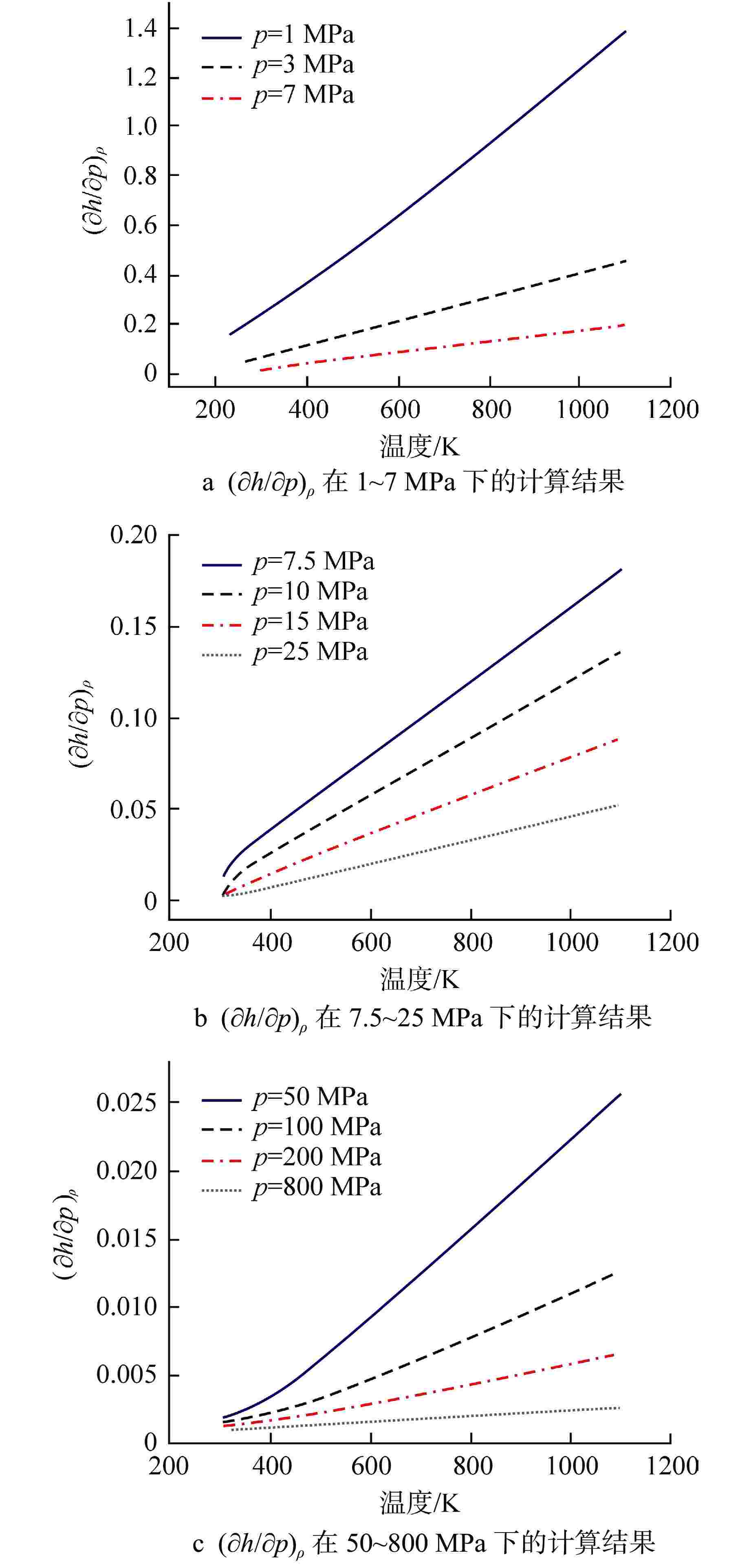
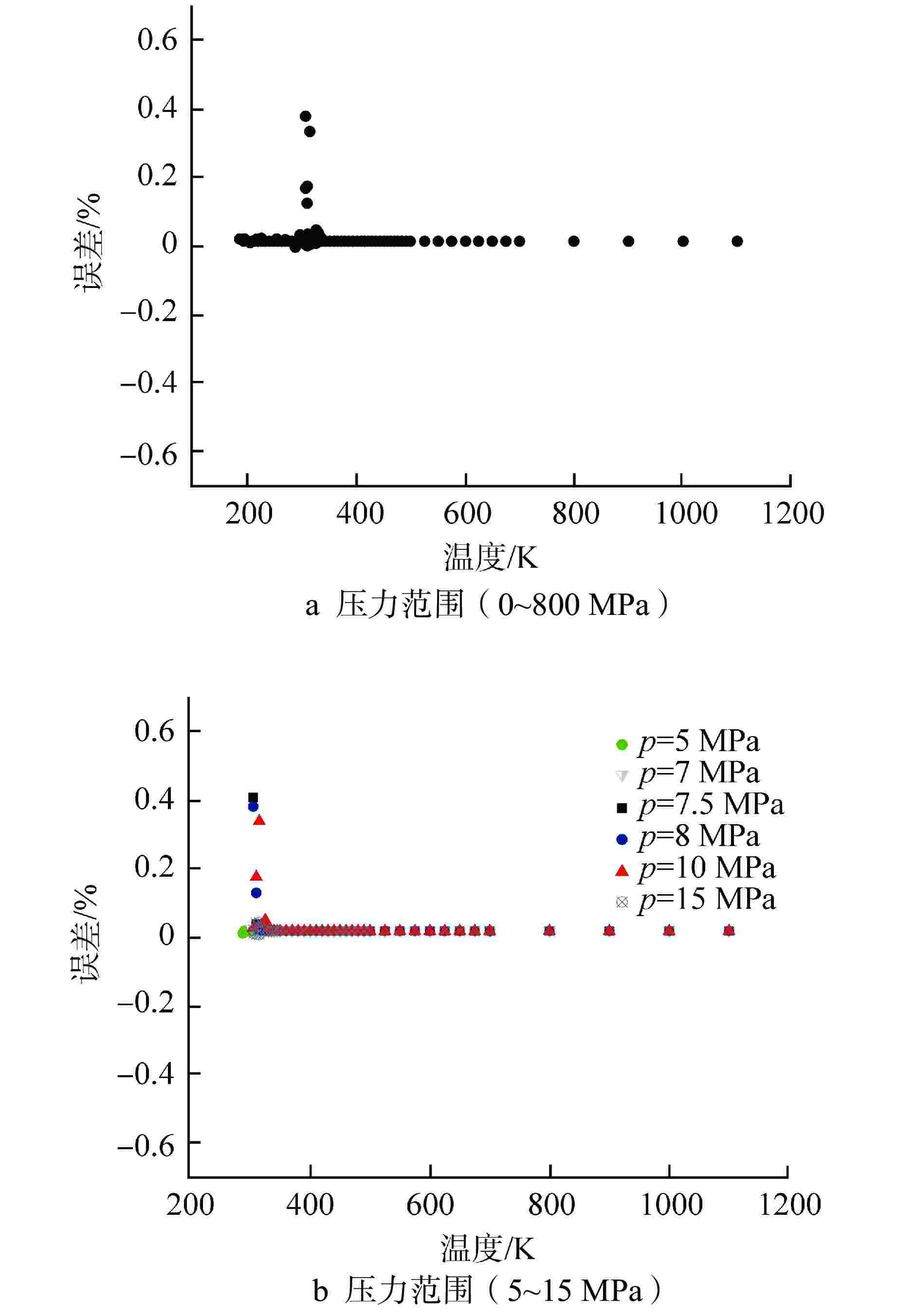
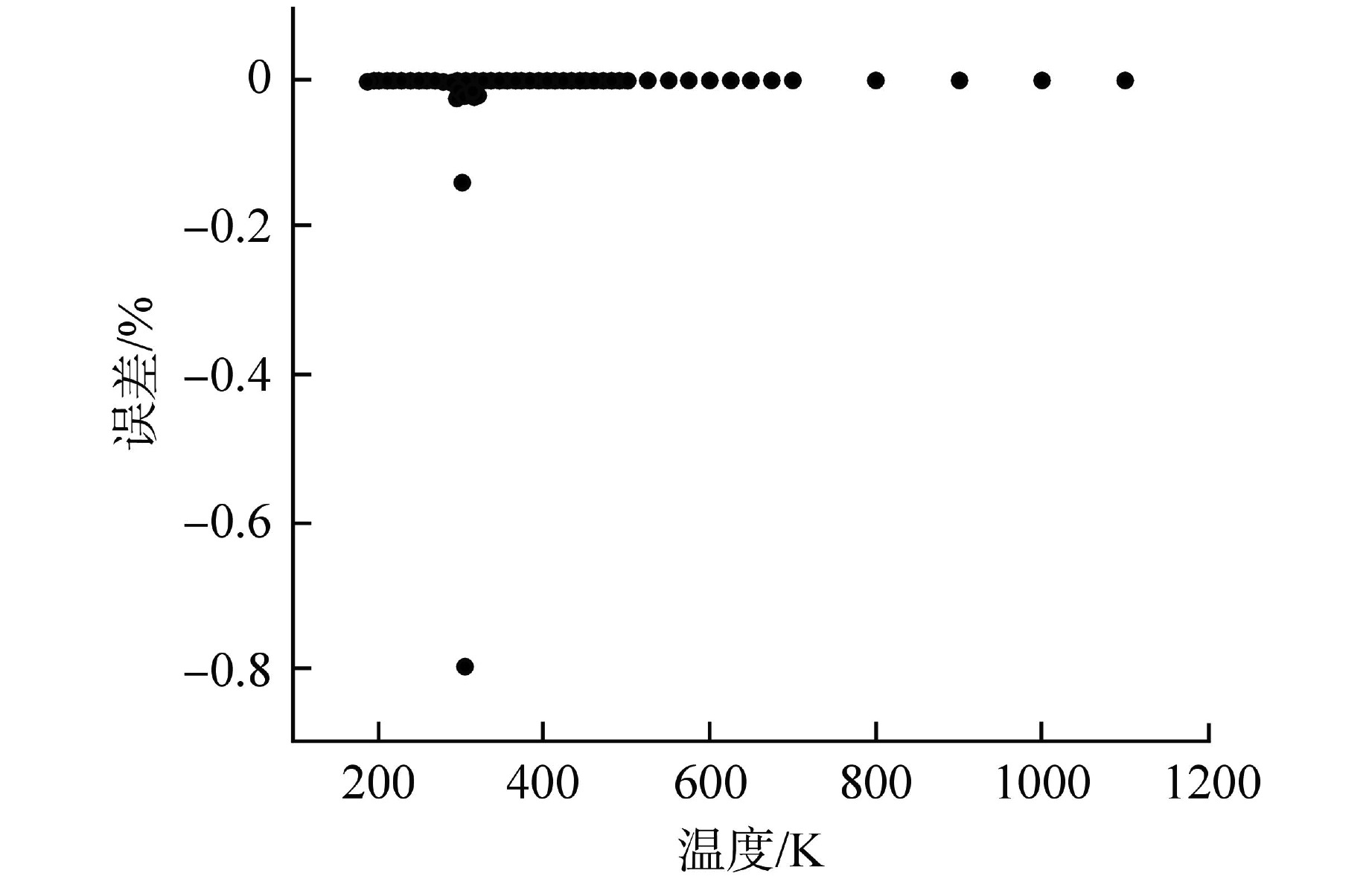
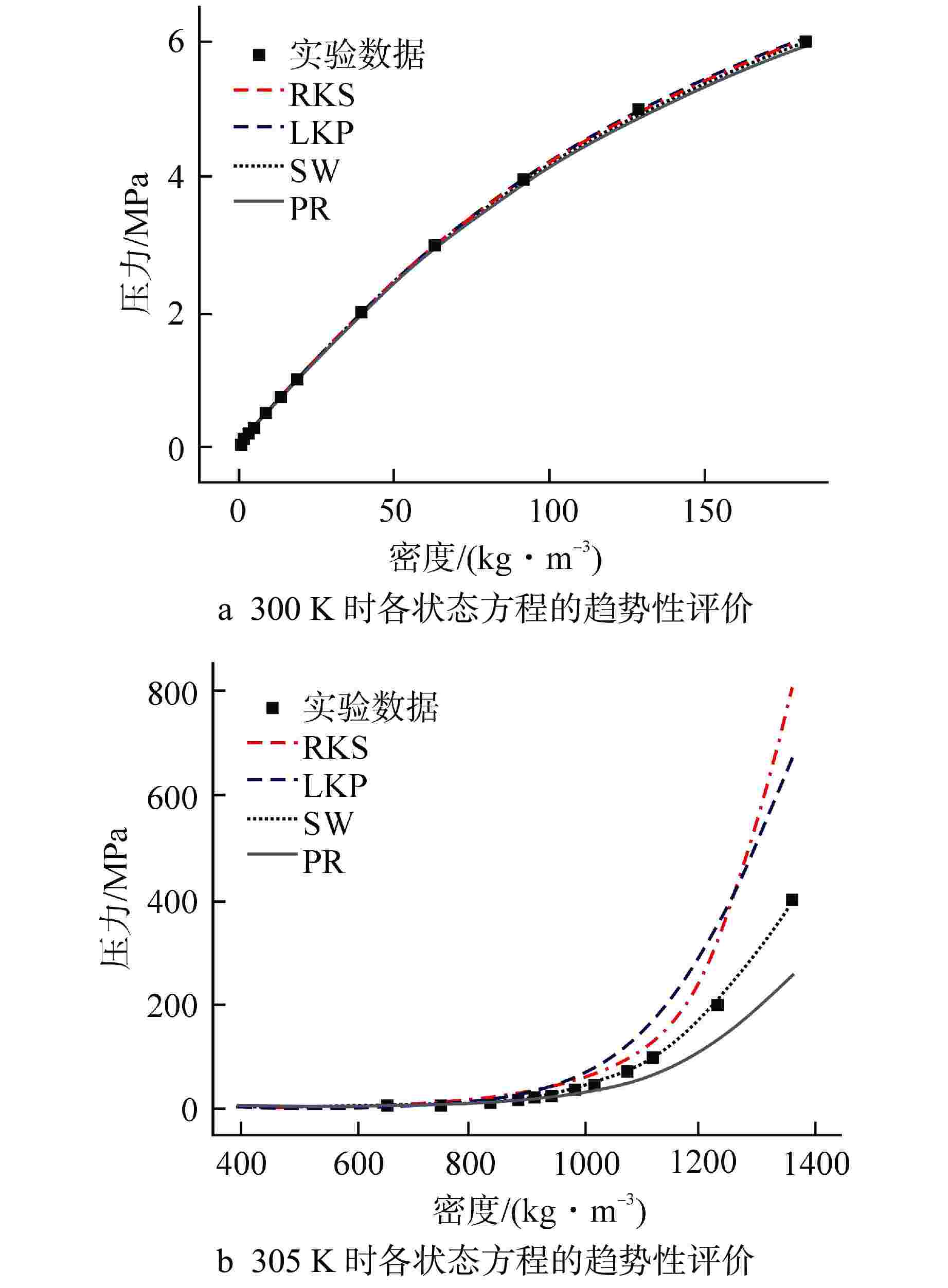
摘要: 为提高超临界二氧化碳（S-CO2）布雷顿循环方程的求解精度，需采用全隐式或半隐式差分格式对流体守恒方程进行离散求解，而偏导物性对于隐式求解不可或缺。本研究将评价目前最典型的二氧化碳气体状态方程在全参数范围内的准确性，在此基础上通过Maxwell方程推导二氧化碳气体的偏导物性关联式，并采用定义值评价其闭合性。研究结果表明：①SW方程在亚临界与超临界区域内准确度最高，误差保持在3%以内；②在SW方程以及Maxwell方程的基础上推导了温度为216~1100 K、压力为0~800 MPa时，二氧化碳气体偏导物性(∂h/∂ρ)p、(∂h/∂p)ρ的关联式；③(∂h/∂ρ)p、(∂h/∂p)ρ绝大多数数据点的误差都保持在±0.01%以内，在临界点附近误差稍有增大，(∂h/∂ρ)p的最大误差为0.373%，(∂h/∂p)ρ的最大误差为−0.798%。Abstract: To improve the accuracy of solving the Brayton Cycle equation of supercritical carbon dioxide (S-CO2), the fully implicit or semi-implicit difference scheme is used to solve the fluid conservation equation discretely, and the partial derivative property is indispensable for the implicit solution. This study will evaluate the accuracy of the most typical state equation of carbon dioxide gas in the full parameter range. On this basis, the Maxwell equation is used to derive the partial derivative correlation of carbon dioxide gas. The results show that:①the SW equation has the highest accuracy in subcritical and supercritical regions, and the error is kept within 3%; ②based on the SW equation and Maxwell equation, the correlations of (∂h/∂ρ)p and (∂h/∂p)ρ of carbon dioxide gas at 216~1100 K and 0 ~800 MPa are derived; ③ the error of most data points of (∂h/∂ρ)p and (∂h/∂p)ρ remains within ±0.01%, and the error increases slightly near the critical point. The maximum error of (∂h/∂ρ)p is 0.373%, and the maximum error of (∂h/∂p)ρ is −0.798%.
-
Key words:
- Carbon dioxide /
- Partial derivative property /
- Derivation /
- Evaluation
-
图 3 焓在定压条件下对密度的偏导数曲线
Figure 3. Partial Derivative Curve of Enthalpy Versus Density at Constant Pressure
图 4 焓在定密度条件下对压力的偏导数曲线
Figure 4. Partial Derivative Curve of Enthalpy Versus Pressure under Constant Density
图 5 二氧化碳(∂h/∂ρ)p在216~1100 K和0~800 MPa的误差
Figure 5. Error of (∂h/∂ρ)p of Carbon Dioxide at 216~1100 K and 0~800 MPa
图 6 二氧化碳(∂h/∂p)ρ在216~1100 K和0~800 MPa的误差
Figure 6. Error of (∂h/∂p)ρ of Carbon Dioxide at 216~1100 K and 0~800 MPa
表 1 不同类型二氧化碳气体状态方程
Table 1. Different Types of Carbon Dioxide Gas Equations of State
代表方程 关联式 RKS[4] $p = \dfrac{ { {R}T} }{ {v - b} } - \dfrac{ {a(T)} }{ {v(v + b)} }$ PR[5] $p = \dfrac{ { {R }T} }{ {v - b} } - \dfrac{ {a(T)} }{ {v(v + b) + b(v - b)} }$ LKP[6] $\dfrac{ { {p_r}{v_r} } }{ { {T_r} } } = 1 + \dfrac{B}{ { {v_r} } } + \dfrac{C}{ { {v_r^2} } } + \dfrac{D}{ { {v_r^5}} }{\text{ + } }\dfrac{ { {c_4} } }{ { {T_r^3}{v_r^2} } }\left(\beta + \dfrac{\gamma }{ { {v_r^2} } }\right)\exp \left( - \dfrac{\gamma }{ { {v_r^2} } }\right)$ SW[7] $p = \rho {R}T(1 + \delta {\phi ^r_\delta} )$ 
下载: 导出CSV
-
[1] 徐前,陈洪溪. 超临界二氧化碳闭式布雷顿循环特点与应用[J]. 发电设备,2019, 33(5): 320-324,330. [2] THORADE M, SAADAT A. Partial derivatives of thermodynamic state properties for dynamic simulation[J]. Environmental Earth Sciences, 2013, 70(8): 3497-3503. doi: 10.1007/s12665-013-2394-z [3] 单建强,秋穗正,朱继洲,等. 安全分析用钠物性偏导数公式的推导研究[J]. 核动力工程,1997, 18(3): 238-243. [4] SOAVE G. Equilibrium constants from a modified Redlich-Kwong equation of state[J]. Chemical Engineering Science, 1972, 27(6): 1197-1203. doi: 10.1016/0009-2509(72)80096-4 [5] PENG D Y, ROBINSON D B. A new two-constant equation of state[J]. Minerva Ginecologica, 1976, 12(1): 3069-3078. [6] PLOCKER U, KNAPP H, PRAUSNITZ J. Calculation of high-pressure vapor-liquid equilibria from a corresponding-states correlation with emphasis on asymmetric mixtures[J]. Industrial & Engineering Chemistry Process Design and Development, 1978, 17(3): 324-332. [7] SPAN R, WAGNER W. A new equation of state for carbon dioxide covering the fluid region from the triple-point temperature to 1100 K at pressures up to 800 MPa[J]. Journal of Physical and Chemical Reference Data, 1996, 25(6): 1509-1596. doi: 10.1063/1.555991 [8] NOWAK P, TIELKES T, KLEINRAHM R, et al. Supplementary measurements of the (p, ρ, T) relation of carbon dioxide in the homogeneous region at T=313 K and on the coexistence curve at T=304 K[J]. The Journal of Chemical Thermodynamics, 1997, 29(8): 885-889. doi: 10.1006/jcht.1997.0208 [9] KLIMECK J, KLEINRAHM R, WAGNER W. Measurements of the(p, ρ, T) relation of methane and carbon dioxide in the temperature range 240 K to 520 K at pressures up to 30 MPa using a new accurate single-sinker densimeter[J]. The Journal of Chemical Thermodynamics, 2001, 33(3): 251-267. doi: 10.1006/jcht.2000.0711 [10] 杨思远. 超临界和亚临界CO2的定压比热和密度实验研究[D]. 大连: 大连理工大学, 2020. -
计量
- 文章访问数: 337
- HTML全文浏览量: 37
- PDF下载量: 23
- 被引次数: 0
