Study on Refined Calculation Method for Added Mass of Special-shaped Structures in Complex Fluid Domain
-
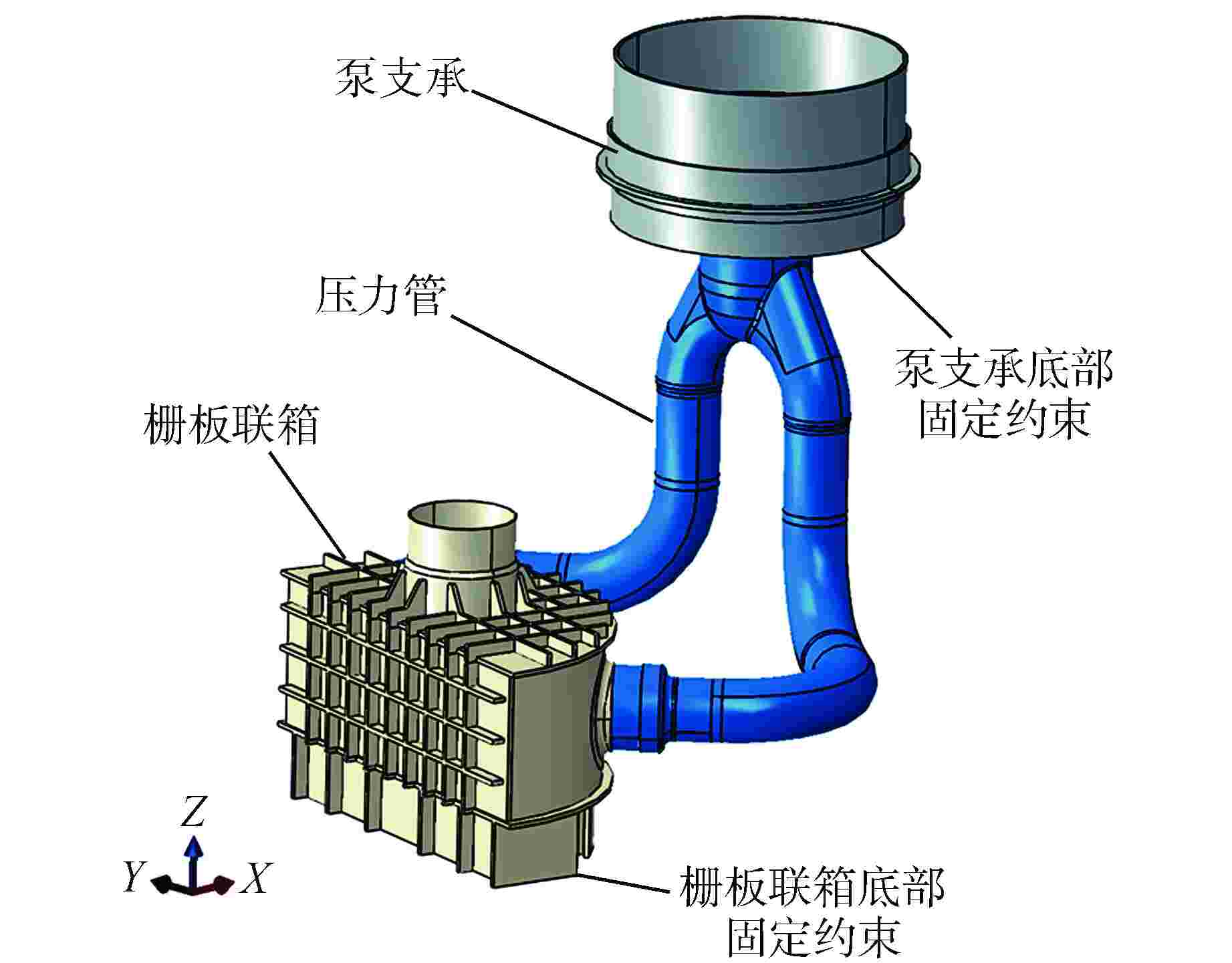
摘要: 反应堆堆内构件工程设计通常采用附加质量方法模拟流体对结构的动力作用。以浸没在复杂流域中某异型压力管为例，提出了一种结构附加质量迭代计算方法，即以声固耦合分析得出的湿模态为基准，综合考虑流体密度和体积模量精细化确定结构附加质量，并讨论了该方法的适用范围。通过压力管1∶1振动试验实测与仿真结果对比，证明了附加质量精细化计算的准确性。结果表明，本文方法能较为精确地获得结构的主频和振型，具有较快的收敛速度，可供类似工程仿真分析参考借鉴。Abstract: The engineering design of reactor internals usually uses the added mass method to simulate the dynamic effects of fluids on the structure. Taking a special-shaped pressure pipe immersed in a complex fluid domain as an example, a structural added mass iterative calculation method is proposed, which uses the wet mode obtained from the acoustic-structure coupling analysis as the benchmark, comprehensively considers the fluid density and bulk modulus to determine the structural added mass, and discusses the applicability of this method. The accuracy of the added mass calculation has been demonstrated by comparing the measured and simulated results of the 1∶1 vibration test of the pressure pipe. The results show that the method proposed in this paper can accurately obtain the main frequency and vibration mode of the structure, and has a fast convergence speed, which can be used as a reference for similar engineering simulation analysis.
-
图 2 压力管3个方向主振型归一化位移
Figure 2. Normalized Displacement of Pressure Pipe for Main Vibration Mode in Three Directions
图 3 压力管结构模型各阶特征频率
Figure 3. Characteristic Frequencies of Each Order of Pressure Pipe Structure Model
图 4 压力管结构模型第20阶位移振型
Figure 4. 20th Order Displacement Vibration Mode of Pressure Pipe Structure Model
表 1 压力管频率计算结果
Table 1. Calculation Results for Pressure Pipe Frequency
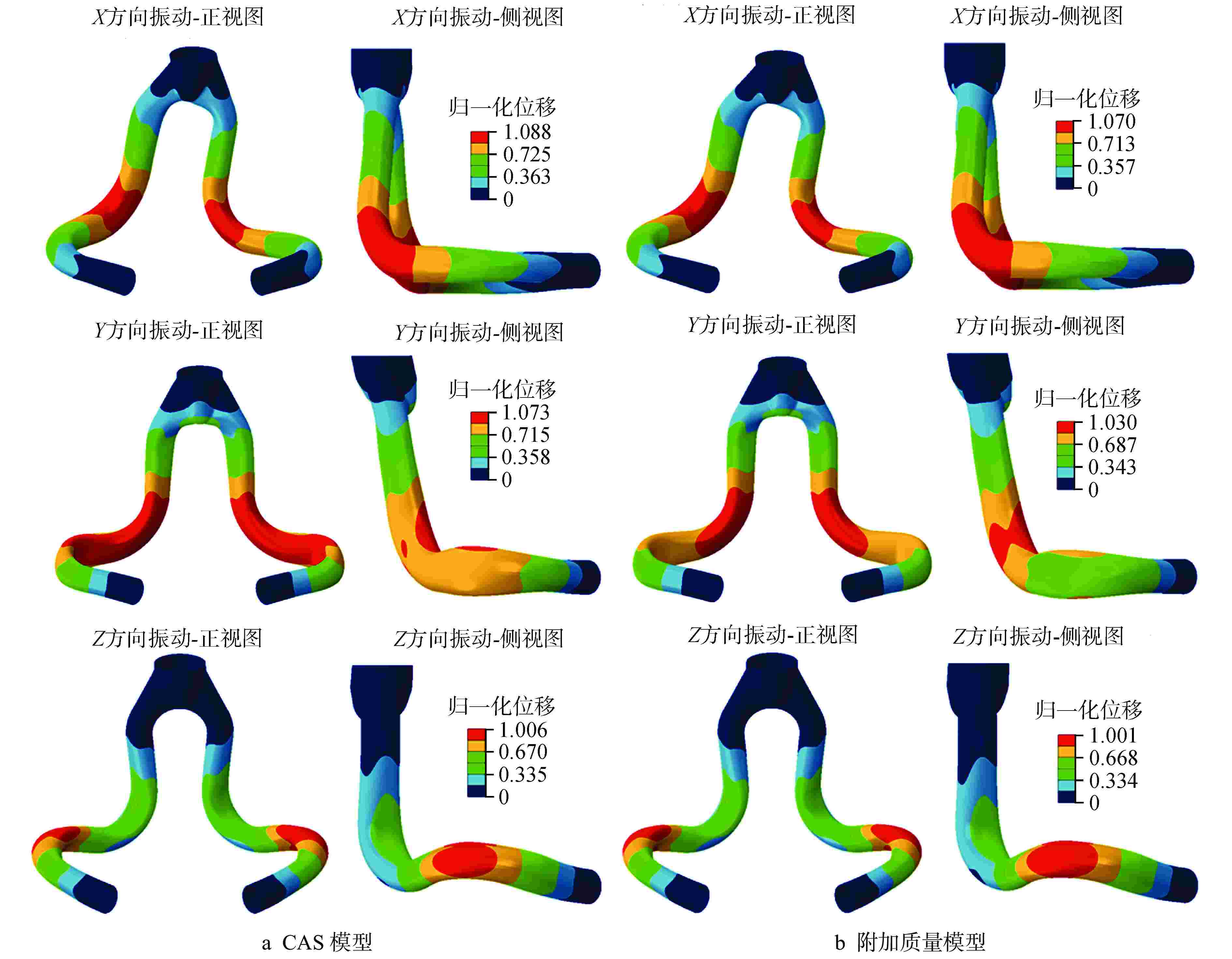
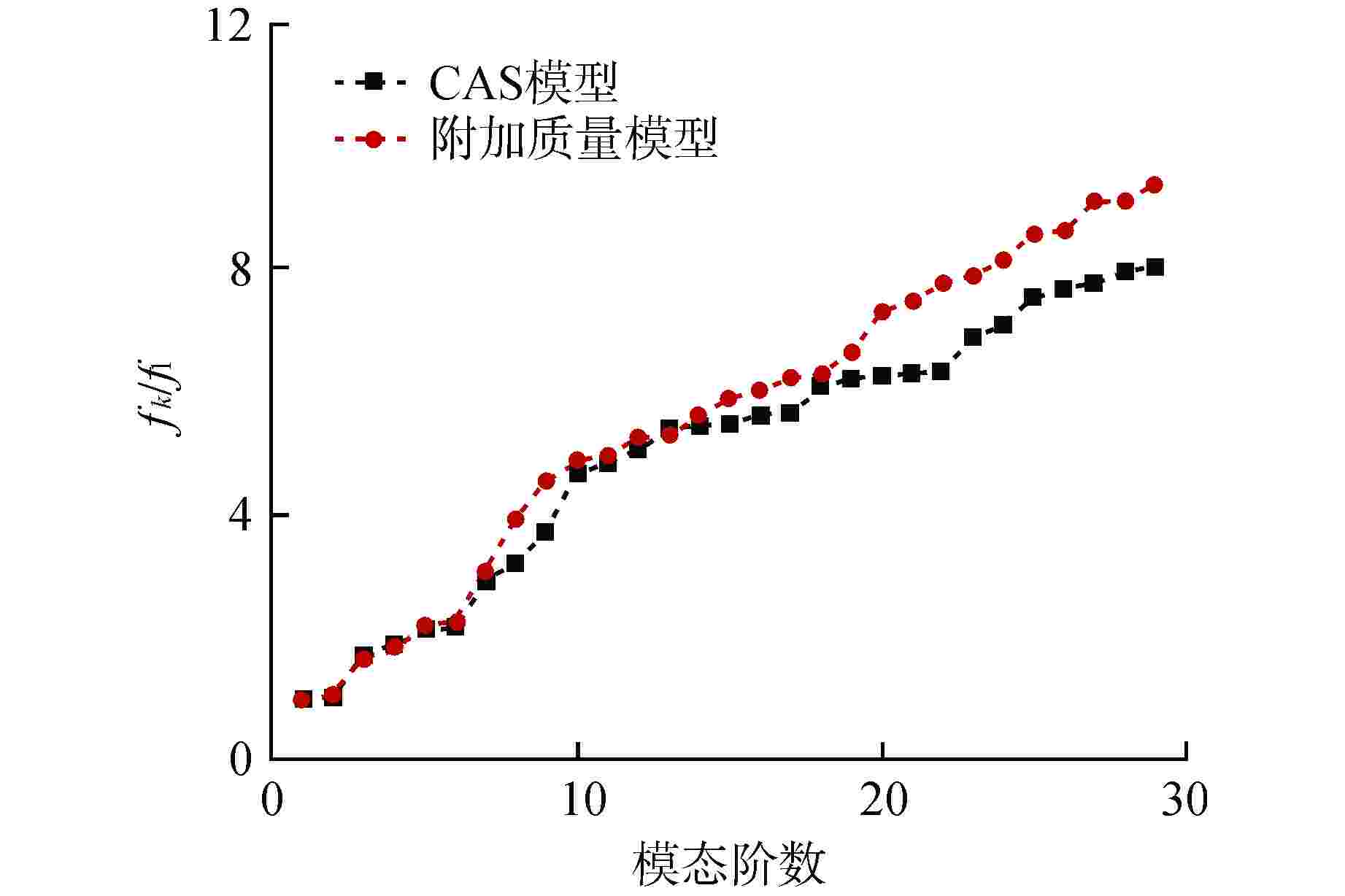
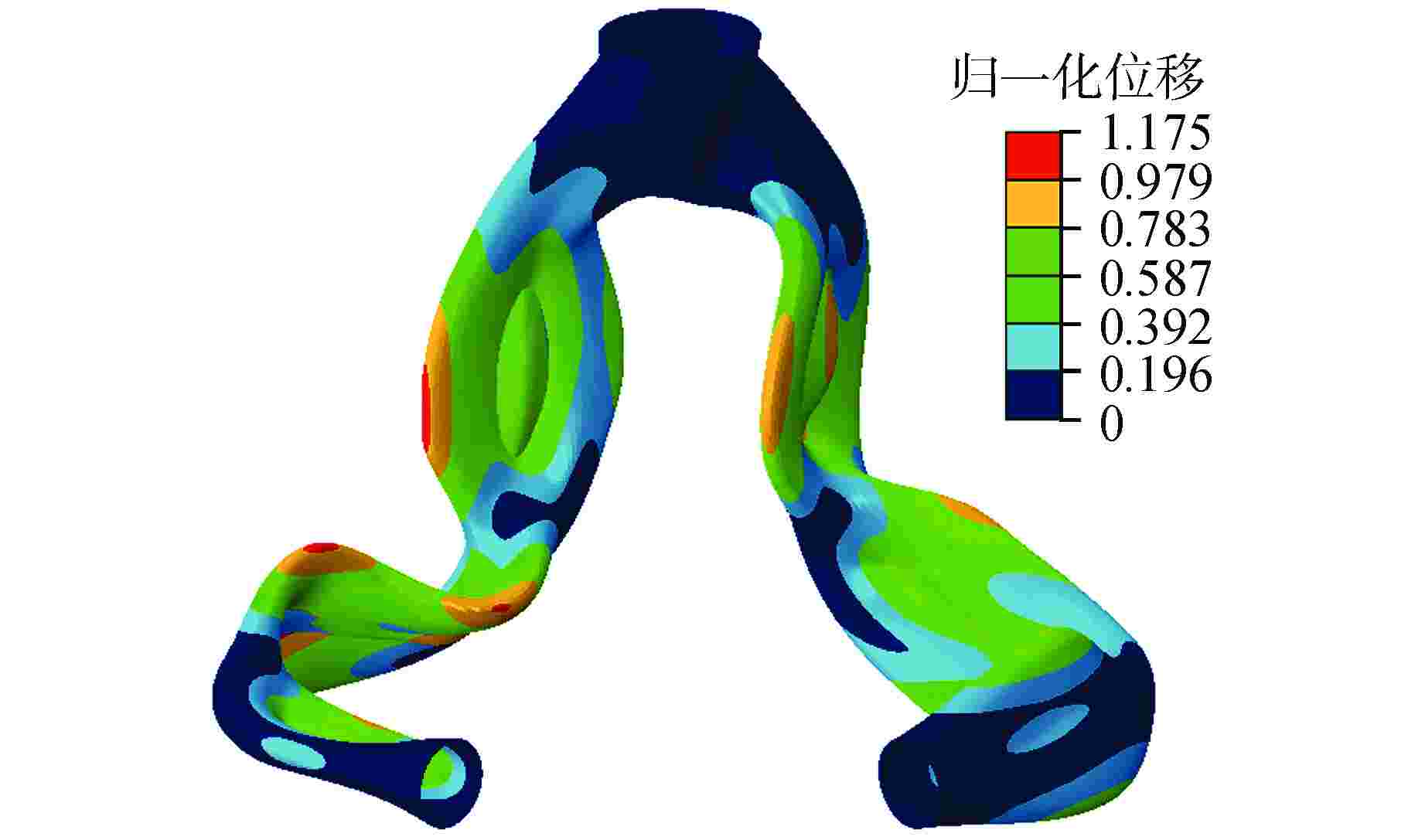
方向 湿模态频率/Hz 干模态（无附加质量） 干模态（含附加质量） 频率/Hz 偏差/% 附加质量系数 频率/Hz 偏差/% 附加质量系数 X 20.049 26.586 32.61 0.758 20.052 0.01 0 Y 34.336 43.931 27.94 0.637 33.134 −3.50 −0.069 Z 43.380 59.452 37.05 0.878 44.841 3.37 0.068 偏差=（干模态频率−湿模态频率）/湿模态频率×100% 
下载: 导出CSV
表 2 压力管试验件固有频率对比结果
Table 2. Comparison Results of Natural Frequencies of Pressure Pipe Test Piece
方向 固有频率实
测值/Hz实测
值降
幅/%固有频率仿
真值/Hz仿真
值降
幅/%偏差/% 空气中 水中 空气中 水中 空气中 水中 X 17.885 9.849 44.93 19.272 11.421 40.74 7.76 15.96 Y 24.889 17.113 31.24 24.435 15.376 37.07 −1.82 −10.15 Z 33.181 23.562 28.99 32.687 19.885 39.17 −1.49 −15.61 降幅=（空气中频率−水中频率）/空气中频率×100%；偏差=（仿真值−试验值）/试验值×100%
下载: 导出CSV
-
[1] 杨红义, 余华金, 王月英. 我国钠冷快堆结构力学的发展现状及前景[C]//第十七届全国反应堆结构力学会议论文集. 上海: 中国力学学会, 2012: 11-16. [2] PENG Q, SU X, LI J, et al. Boundary effect on the dynamic response of a 7-hexagon fuel ducts submerged in fluid[J]. Nuclear Engineering and Design, 2020, 370: 110870. doi: 10.1016/j.nucengdes.2020.110870 [3] SARPKAYA T. Vortex-induced oscillations: a selective review[J]. Journal of Applied Mechanics, 1979, 46(2): 241-258. doi: 10.1115/1.3424537 [4] CHEN S S. Fluid damping for circular cylindrical structures[J]. Nuclear Engineering and Design, 1981, 63(1): 81-100. doi: 10.1016/0029-5493(81)90018-2 [5] MULCAHY T M. Fluid forces on rods vibrating in finite length annular regions[J]. Journal of Applied Mechanics, 1980, 47(2): 234-240. doi: 10.1115/1.3153648 [6] BLEVINS R D. Formulas for natural frequency and mode shape[M]. New York: Van Nostrand Reinhold, 1979: 1-16. [7] AU-YANG M K. Generalized hydrodynamic mass for beam mode vibration of cylinders coupled by fluid gap[J]. Journal of Applied Mechanics, 1977, 44(1): 172-173. doi: 10.1115/1.3423989 [8] PETTIGREW M J, TAYLOR C E, KIM B S. Vibration of tube bundles in two-phase cross-flow: Part 1—hydrodynamic mass and damping[J]. Journal of Pressure Vessel Technology, 1989, 111(4): 466-477. doi: 10.1115/1.3265705 [9] PAIDOUSSIS M P, MAVRIPLIS D, PRICE S J. A potential-flow theory for the dynamics of cylinder arrays in cross-flow[J]. Journal of Fluid Mechanics, 1984, 146: 227-252. doi: 10.1017/S002211208400183X [10] CHEN S S, CHUNG H. Design guide for calculating hydrodynamic mass. Part I. Circular cylindrical structures: ANL-CT-76-45[R]. Argonne: Argonne National Lab. , 1976. [11] FRITZ R J. The effect of liquids on the dynamic motions of immersed solids[J]. Journal of Engineering for Industry, 1972, 94(1): 167-173. doi: 10.1115/1.3428107 [12] EVERSTINE G C. Finite element formulatons of structural acoustics problems[J]. Computers & Structures, 1997, 65(3): 307-321. [13] RODRIGUEZ C G, FLORES P, PIERART F G, et al. Capability of structural–acoustical fsi numerical model to predict natural frequencies of submerged structures with nearby rigid surfaces[J]. Computers & Fluids, 2012, 64: 117-126. [14] RAWAT A, MATSAGAR V, NAGPAL A K. Finite element simulation of cylindrical liquid storage tank under tri-directional components of earthquake[J]. Journal of Structural Engineering, 2015, 42(1): 28-39. [15] ENERGOATOMIZDAT. Standards for strength calculations for equipment and pipelines in nuclear power facilities: PNAE G-7-002-86[S]. Moscow: Energoatomizdat, 1989: 510-515. -
计量
- 文章访问数: 138
- HTML全文浏览量: 56
- PDF下载量: 30
- 被引次数: 0
