堆内构件流致振动试验支承多目标优化设计

张宇; 李朋洲; 乔红威; 缪雨菡; 高李霞; 喻丹萍; 孙磊

doi:10.13832/j.jnpe.2023.04.0116

堆内构件流致振动试验支承多目标优化设计

doi: 10.13832/j.jnpe.2023.04.0116

中国核动力研究设计院，成都，610213

详细信息

作者简介:
张宇（1996—），男，助理研究员，博士研究生，现主要从事反应堆结构流致振动研究，E-mail: npic_zy@163.com

通讯作者:
李朋洲，E-mail: pengzhouli@aliyun.com

中图分类号: TL353⁺.9；O342
计量
- 文章访问数: 178
- HTML全文浏览量: 58
- PDF下载量: 28
- 被引次数: 0
出版历程
- 收稿日期: 2022-08-29
- 修回日期: 2023-03-01
- 刊出日期: 2023-08-15

Multi-objective Optimization Design of the Support in Flow Induced Vibration Test of Reactor Internals

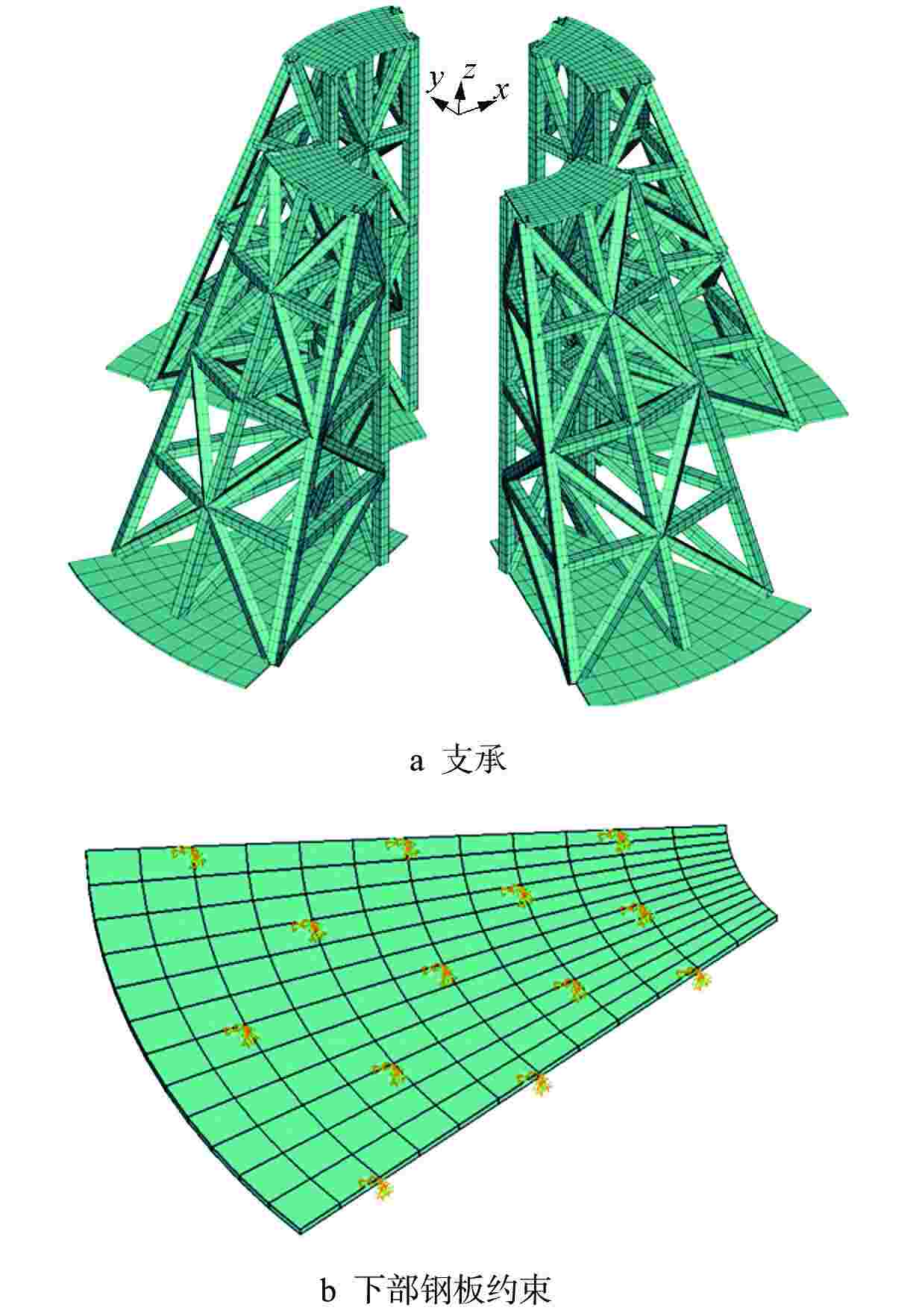
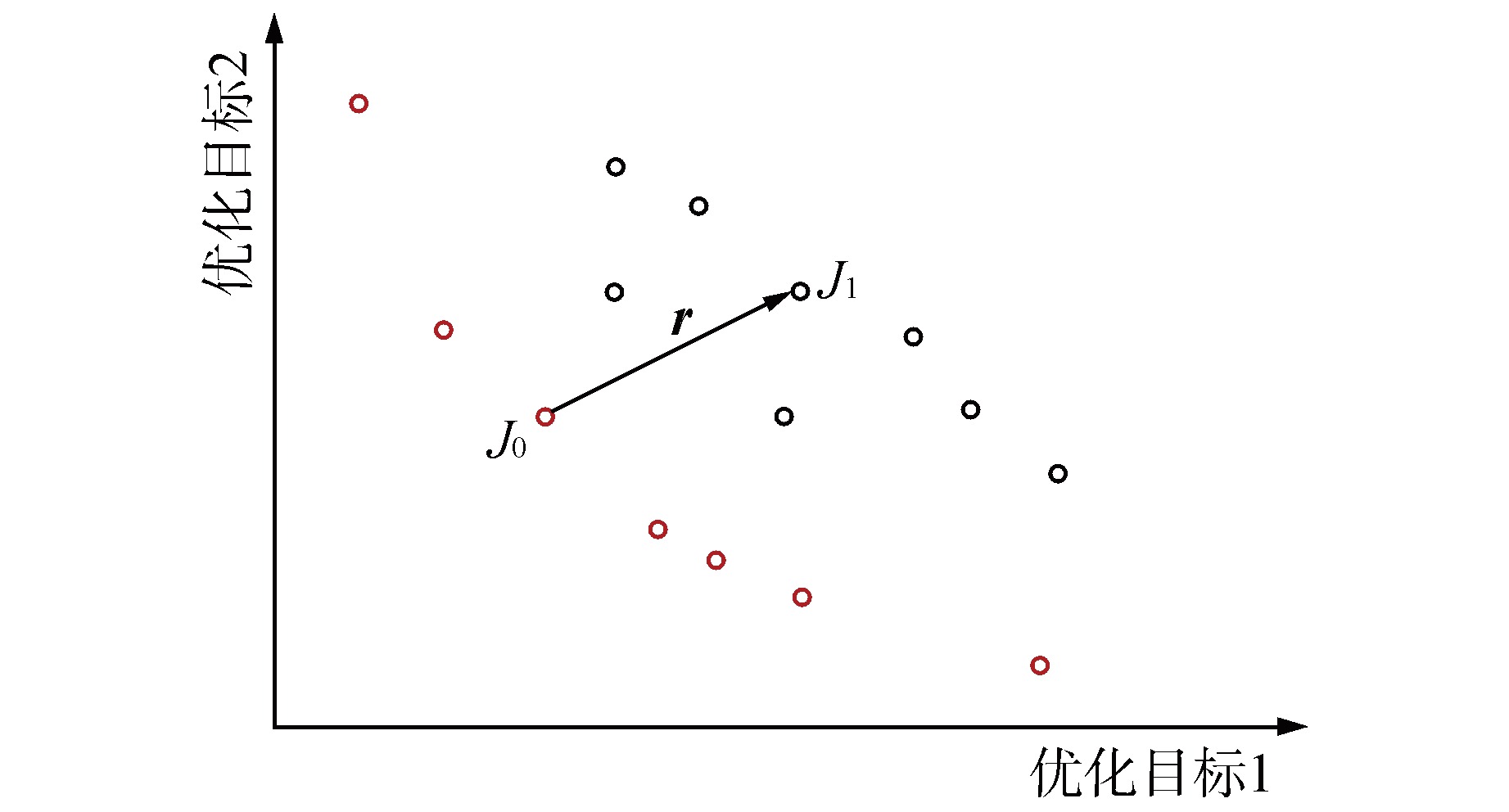
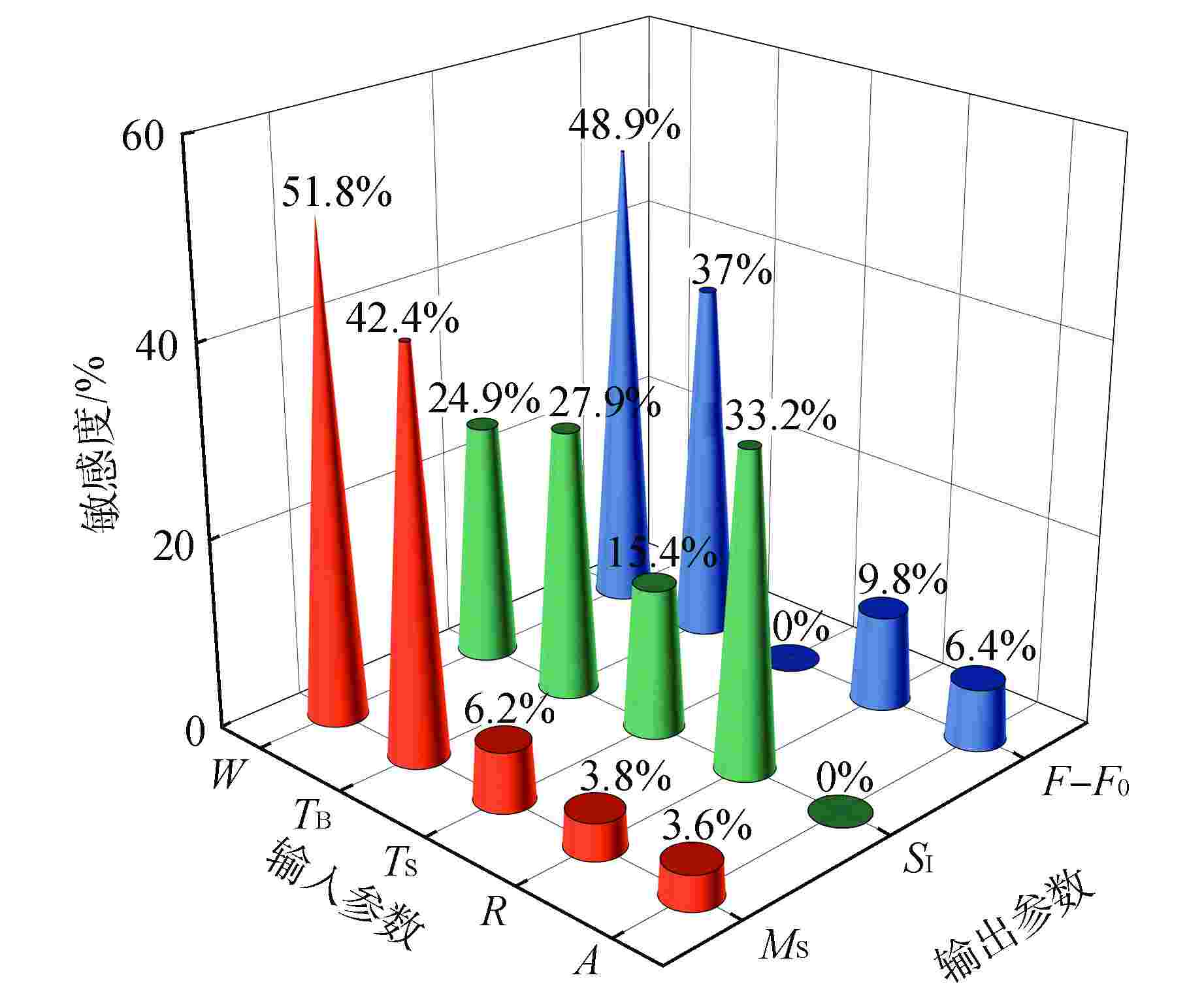
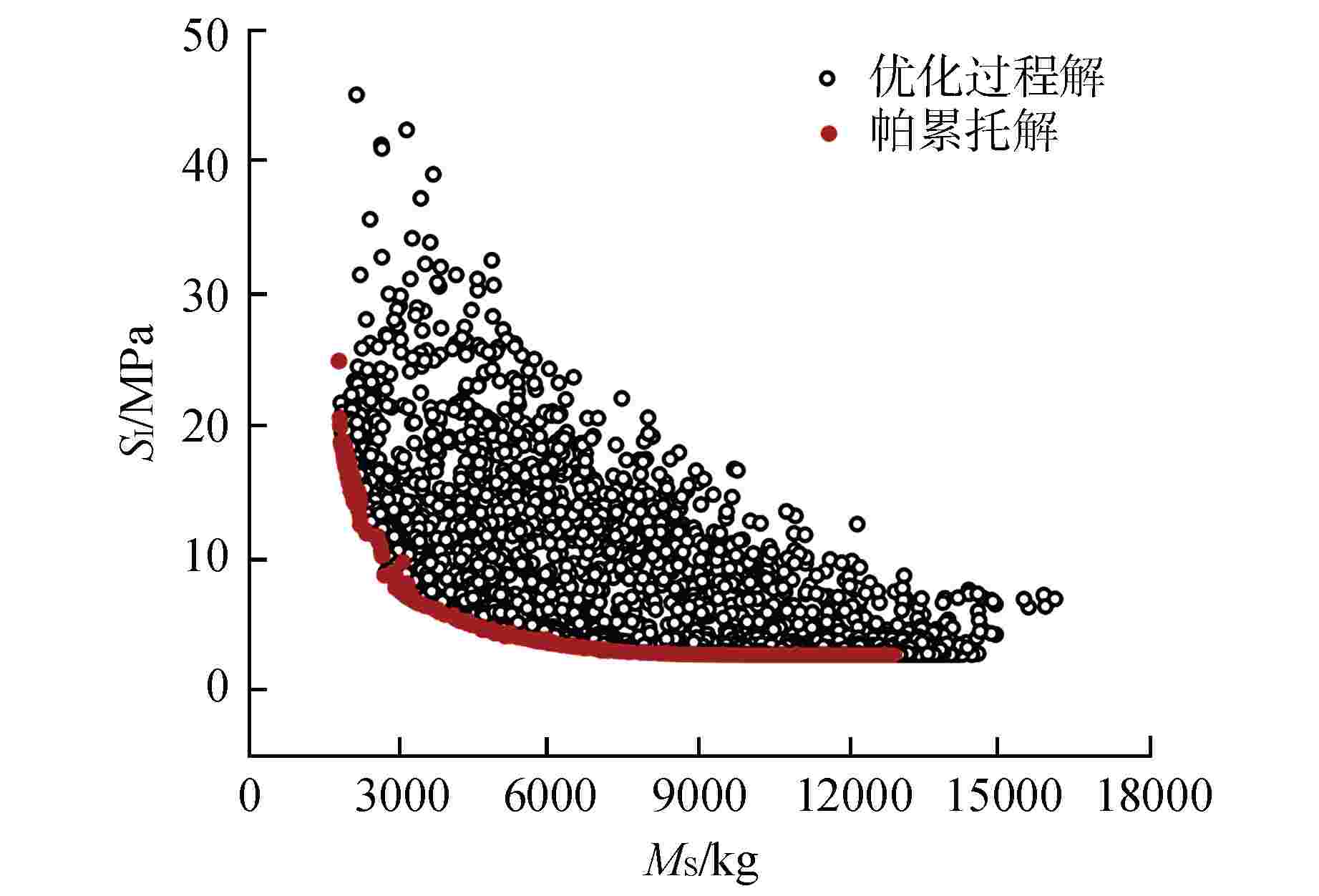
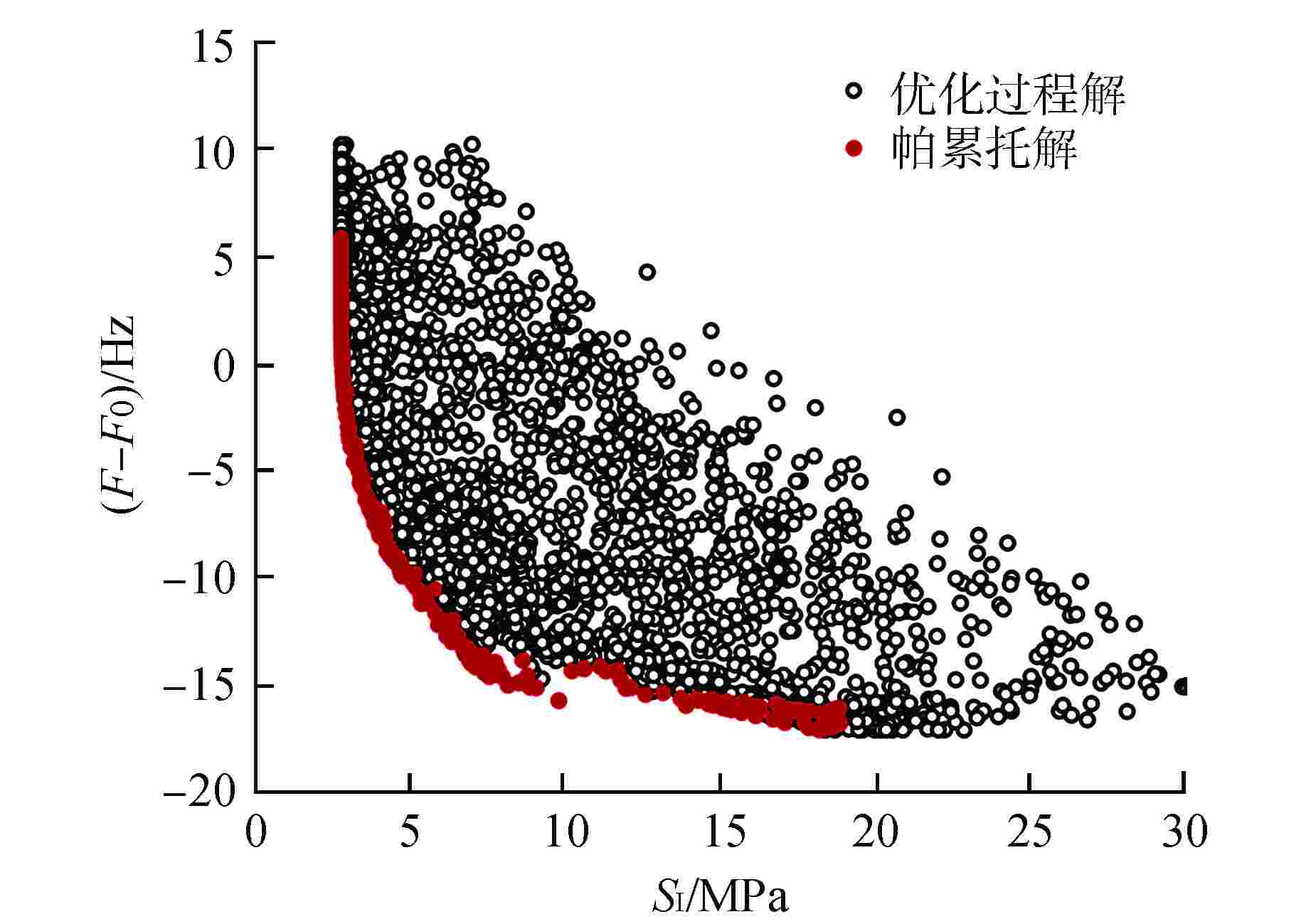
Nuclear Power Institute of China, Chengdu, 610213, China

摘要

摘要: 为充分提升材料利用率和避开堆内构件基阶频率，针对堆内构件流致振动（FIV）试验支承结构开展了基于多目标优化算法的参数寻优研究。首先建立了支承有限元模型，并将支承质量、最大应力强度和基阶频率作为优化目标，然后通过加强帕累托进化算法（SPEA-Ⅱ）对多目标优化问题进行了全局寻优，最终得到输入与输出参数间的全局敏感度和帕累托解集，并给出了可行的支承设计方案。通过对支承开展多目标优化，在保证结构强度的同时显著降低了制造成本，相关研究可为类似的支承设计提供参考。
- 堆内构件 /
- 流致振动（FIV） /
- 支承设计 /
- 多目标优化
Abstract: In order to fully improve the material utilization rate and isolate the fundamental frequency of the reactor internals, a parameter optimization study based on multi-objective optimization algorithm was carried out for the support structure in the flow induced vibration (FIV) test. The finite element model of support was established first, and the support quality, maximum stress intensity and fundamental frequency were regarded as the optimization goals. Then, the strength pareto evolutionary algorithm (SPEA-Ⅱ) was utilized to obtain global optimal solutions. Finally, the global sensitivity between the input and output parameters and pareto solution set were obtained, and a feasible support design scheme was given. By carrying out multi-objective optimization for the support, the manufacturing cost was significantly reduced while the structural strength was guaranteed. The related work can provide reference for similar support design.
- Reactor internals /
- Flow induced vibration(FIV) /
- Support design /
- Multi-objective optimization

HTML全文

图 1 单个支承三维示意图 mm

Figure 1. 3-D Diagram of Single Support

下载: 全尺寸图片幻灯片

图 2 支承有限元模型

Figure 2. Finite Element Model of Support

下载: 全尺寸图片幻灯片

图 3 二维帕累托解示例

红色圆圈—帕累托解；黑色圆圈—一般解

Figure 3. 2-D Pareto Solution

下载: 全尺寸图片幻灯片

图 4 参数全局敏感度

Figure 4. Parameter Global Sensitivity

下载: 全尺寸图片幻灯片

图 5 支承质量-最大应力强度优化结果

Figure 5. Optimization Results of M_S and S_I

下载: 全尺寸图片幻灯片

图 6 最大应力强度-基阶频率差优化结果

Figure 6. Optimization Results of S_I and (F−F₀)

下载: 全尺寸图片幻灯片

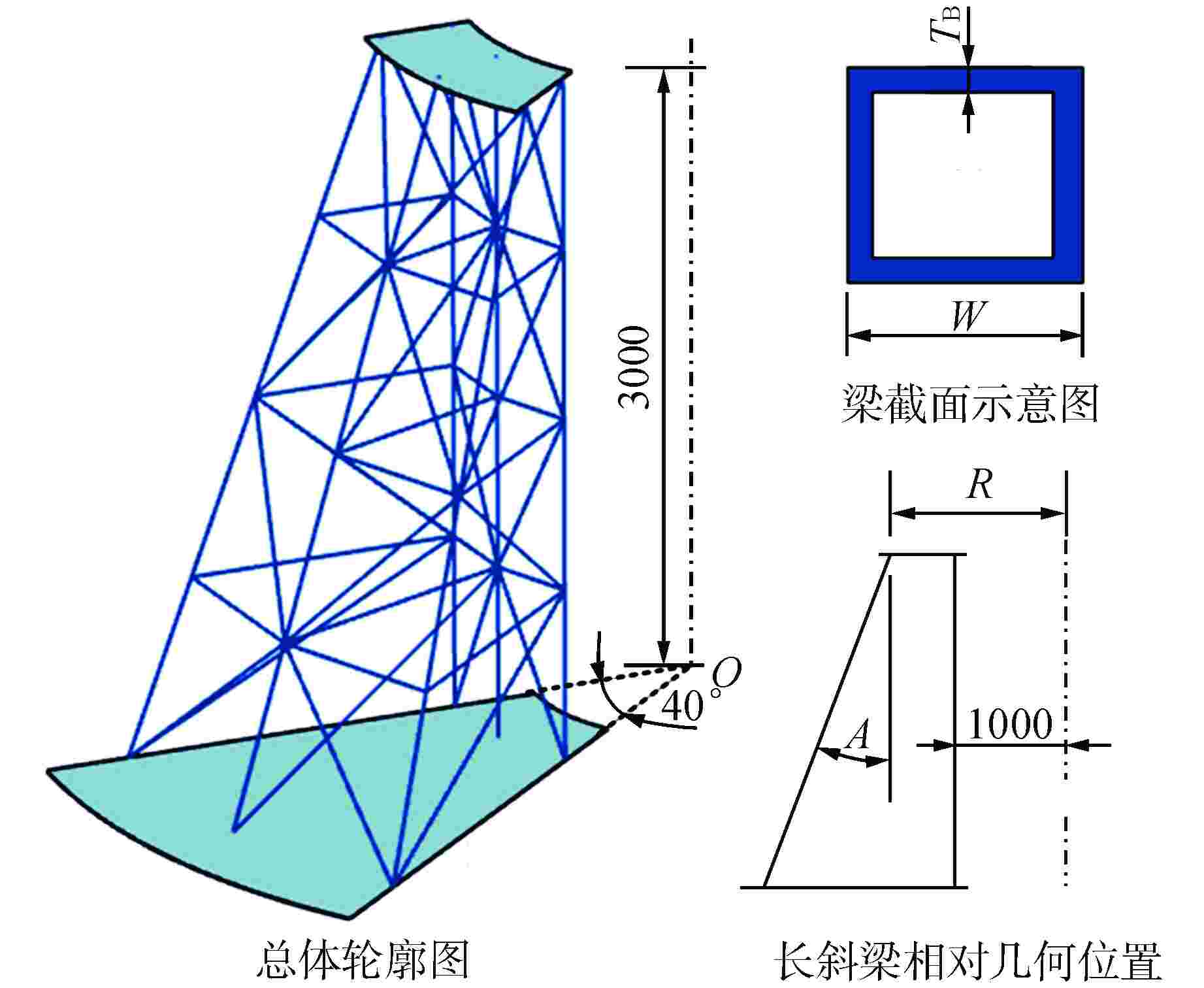
表 1 支承几何变量

Table 1. Alterative Parameters of Support Geometry

可变参数	初始值	取值范围
W/mm	80	40~120
T_B/mm	10	4~16
T_S/mm	20	8~32
R/mm	1300	1100~1500
A	20°	15°~25°

下载: 导出CSV

表 2 支承材料属性

Table 2. Material Properties of Support

材料属性	数值
弹性模量/GPa	210
密度/(kg·m⁻³)	7850
泊松比	0.3

下载: 导出CSV

表 3 支承原始方案与优化方案参数

Table 3. Parameters of Origin and Optimal Supports

方案名称	W/mm	T_B/mm	T_S/mm	R/mm	A
原始方案	80	10	20	1300	20°
方案1	42.7	10.2	8	1354	20°
方案2	63.2	11.9	8	1329	20°
方案3	42.3	6.2	8	1318	20°

下载: 导出CSV

表 4 支承原始方案与优化方案结果对比

Table 4. Results Comparison of Origin and Optimal Supports

输出参数	原始方案	方案1	方案2	方案3
M_S/kg	7131	3347（−53%）	5455（−24%）	2451（−66%）
S_I/MPa	10.2	8.4（−18%）	4.3（−58%）	26.3（158%）
F/Hz	28.1	20.3（−28%）	26.3（−6%）	16.7（−41%）
括号内数值表示与原始方案的相对改变量

下载: 导出CSV

参考文献(15)

[1]	叶献辉,蔡逢春,黄旋,等. 反应堆吊篮在泵致脉动压力载荷下的响应研究[J]. 原子能科学技术,2021, 55(11): 2101-2106. doi: 10.7538/yzk.2020.youxian.0911
[2]	席志德,杨杰,马建中. 华龙一号吊篮1:5模型试验流致振动响应计算分析[J]. 核动力工程,2019, 40(S1): 71-74. doi: 10.13832/j.jnpe.2019.S1.0071
[3]	ZHANG Y, HE C, SUN L. Mathematical model for predicting the vibration performance of a core barrel considering the interaction of seismic load and fluid force[J]. Nuclear Engineering and Design, 2021, 383: 111429. doi: 10.1016/j.nucengdes.2021.111429
[4]	喻丹萍,马建中,席志德,等. 反应堆堆内构件流致振动试验研究综述[J]. 核动力工程,2016, 37(S2): 47-51. doi: 10.13832/j.jnpe.2016.S2.0047
[5]	杨杰,席志德,喻丹萍,等. 华龙一号堆内构件流致振动试验研究[J]. 核动力工程,2016, 37(S2): 37-39. doi: 10.13832/j.jnpe.2016.S2.0037
[6]	KO D Y, KIM K H. Measurement of vibration and stress for APR-1400 reactor internals[J]. Nuclear Engineering and Technology, 2018, 50(6): 963-970. doi: 10.1016/j.net.2018.04.012
[7]	钟自锋,徐国权,聂鹏. 发动机ECU支架振动疲劳分析及其优化设计[J]. 机械设计与研究,2018, 34(3): 100-102,107. doi: 10.13952/j.cnki.jofmdr.2018.0110
[8]	邢广鹏,孙志刚,崔向敏,等. 多工况载荷下航空发动机支架拓扑优化设计[J]. 航空动力学报,2020, 35(11): 2248-2262. doi: 10.13224/j.cnki.jasp.2020.11.002
[9]	NI X J, HAN S B, GE J, et al. Optimization of the gravity support in CFETR vacuum vessel[J]. Fusion Engineering and Design, 2021, 172: 112921. doi: 10.1016/j.fusengdes.2021.112921
[10]	龚曙光, 谢桂兰, 黄云清. ANSYS参数化编程与命令手册[M]. 北京: 机械工业出版社, 2009: 1-11.
[11]	ZITZLER E, LAUMANNS M, THIELE L. SPEA2: improving the strength pareto evolutionary algorithm: Technical Report 103[R]. ETH Zurich: Computer Engineering and Networks Laboratory, 2001.
[12]	JASZKIEWICZ A. Many-objective Pareto local search[J]. European Journal of Operational Research, 2018, 271(3): 1001-1013. doi: 10.1016/j.ejor.2018.06.009
[13]	张宇,孙磊,何超,等. 基于改进BP神经网络的节流孔板空化特性预测[J]. 核动力工程,2021, 42(6): 135-140. doi: 10.13832/j.jnpe.2021.06.0135
[14]	ANSYS, Inc. Theory reference. ANSYS release 5.6[M]. 11th ed. Canonsburg: Tecnology Drive, 1999: 1083-1100.
[15]	BORGONOVO E, PLISCHKE E. Sensitivity analysis: a review of recent advances[J]. European Journal of Operational Research, 2016, 248(3): 869-887. doi: 10.1016/j.ejor.2015.06.032