An Approach for Dynamic Reliability Assessment of Reactor Trip System of HPR1000
-
摘要: 反应堆紧急停堆系统（RTS）结构复杂，导致其具有动态交互、时间依赖和概率不确定性等特性，传统的静态可靠性评估方法难以表征这3个特性。针对这一问题，提出了一种“华龙一号”RTS动态可靠性评估新方法：首先，应用动态故障树（DFT）建立表征RTS动态交互性的DFT模型；然后，在已建立的DFT模型基础上，应用动态贝叶斯网络（DBN）和模糊集理论（FST）建立表征RTS动态交互、时间依赖和概率不确定性的模糊DBN模型；最后，应用拉丁超立方抽样（LHS）定义一个新的模糊贝叶斯推理算法。应用该算法进行模糊贝叶斯正向推理和逆向推理，计算得到了RTS动态可靠度，识别了RTS薄弱环节，并将定义的模糊贝叶斯推理算法与传统的模糊贝叶斯推理算法进行比较，验证了本文定义的算法的准确性和精度。以上研究成果为进一步提高“华龙一号”RTS的可靠性提供了科学依据。Abstract: The structure of reactor trip system (RTS) is complex, which leads to its dynamic interaction, time dependence and probability uncertainty. However, the traditional static reliability assessment methods are difficult to characterize these three characteristics. To solve this problem, a novel approach for dynamic reliability assessment of the RTS of Hualong Pressurized Reactor 1000 (HPR1000) was proposed. Firstly, the dynamic fault tree (DFT) was used to establish the DFT model for the characterization of RTS dynamic interaction. Then, dynamic Bayesian network (DBN) and fuzzy set theory (FST) were used to establish fuzzy DBN model based on the established DFT model for the characterization of dynamic interaction, time dependence and probability uncertainty of the RTS. Finally, Latin hypercube sampling (LHS) was used to define a new fuzzy Bayesian inference algorithm. The defined algorithm was used to carry out the fuzzy Bayesian forward inference and backward inference, the dynamic reliability of RTS was calculated, and the weak points of RTS were identified. Comparing the defined fuzzy Bayesian inference algorithm with the traditional fuzzy Bayesian inference algorithm, the accuracy and precision of the algorithm defined in this paper were verified. The obtained research results provide a scientific basis for further improving the reliability of the RTS of HPR1000.
-
图 1 “华龙一号”RTS结构简图
PIP—信号预处理单元；APU—信号采集和处理单元
Figure 1. Schematic Diagram of RTS Structure of HPR1000
图 4 不考虑维修条件下的“华龙一号”RTS动态可靠度频数直方图
Figure 4. Frequency Histogram for Dynamic Reliability of HPR1000 RTS without Considering Maintenance
图 5 考虑维修条件下的“华龙一号”RTS动态可靠度频数直方图
Figure 5. Frequency Histogram for Dynamic Reliability of HPR1000 RTS with Considering Maintenance
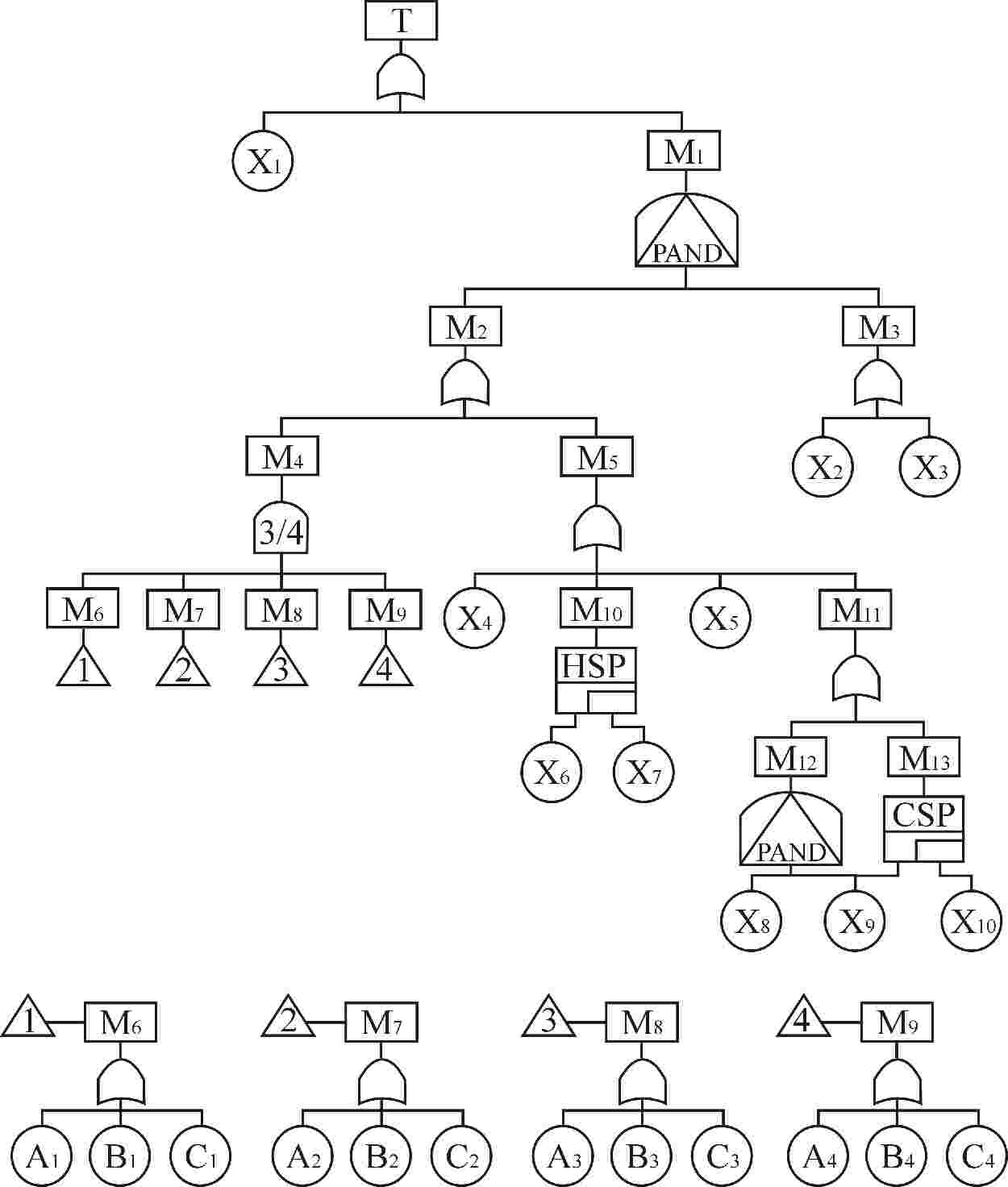
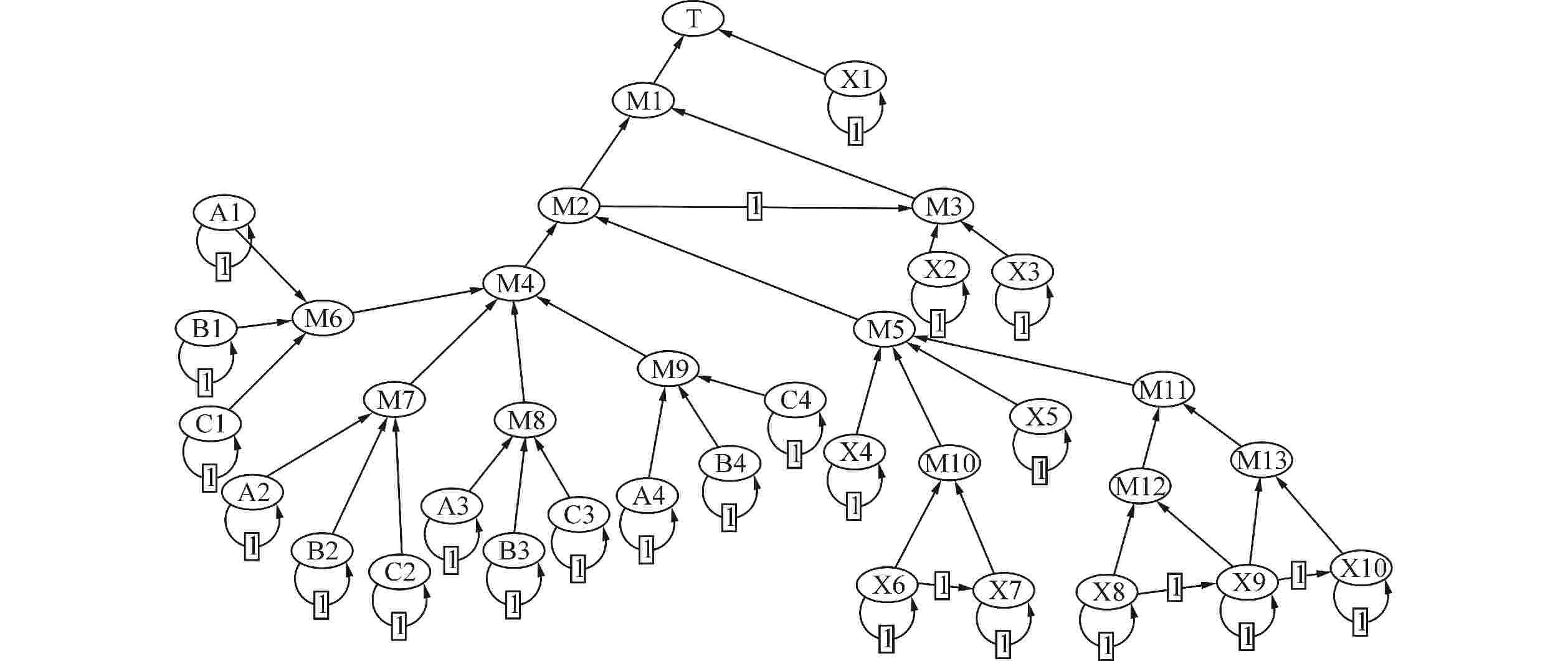
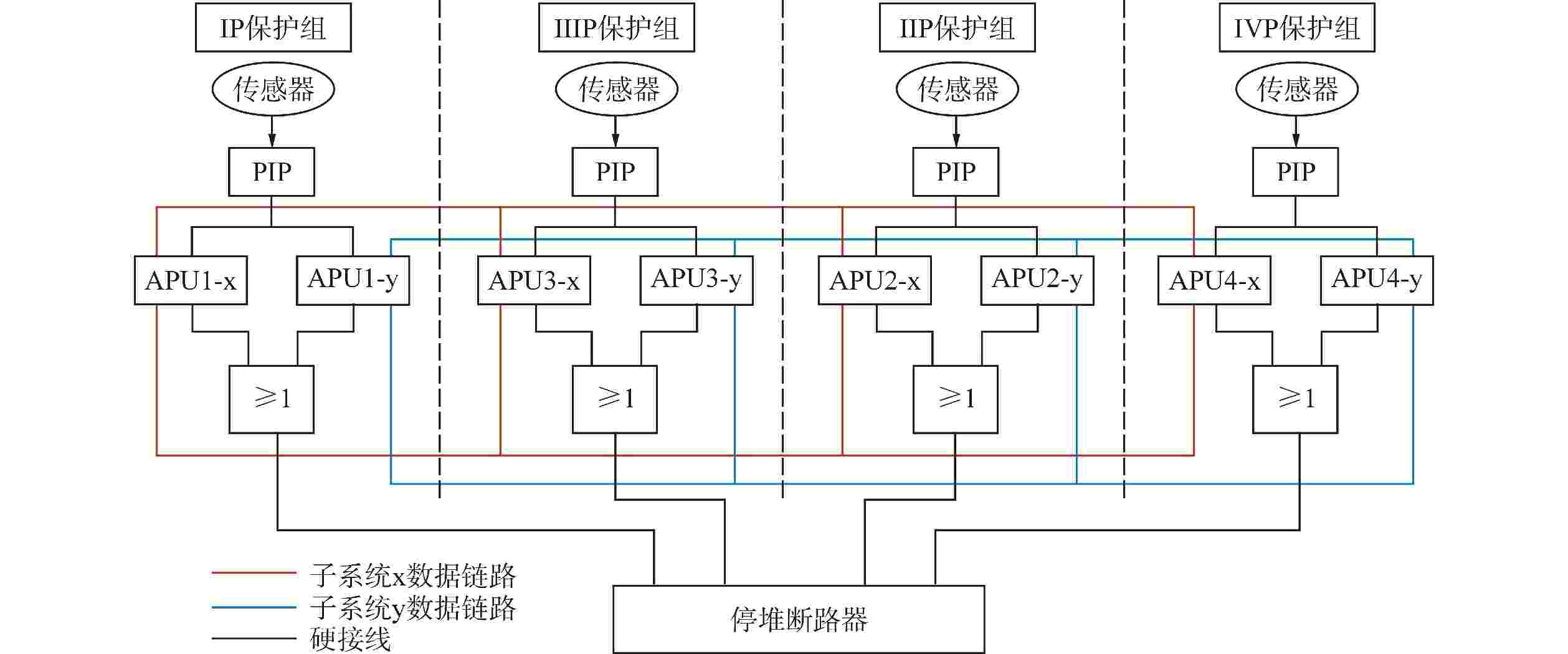
表 1 图2中的编号及描述
Table 1. Number and Description in Figure 2
编号 描述 编号 描述 编号 描述 T IP通道停堆断路器开启失效 M11 供电失效 X5 机架失效 M1 停堆信号失效 M12 传感器先于主电源失效 X6和X7 主、备处理器失效 M2和M3 自动、手动停堆信号失效 M13 电源备份失效 X8 APU传感器失效 M4 逻辑表决失效 X1 IP通道停堆断路器拒开 X9和X10 主、备电源失效 M5 APU失效 X2 人因失误 A1、A2、A3和A4 IP、IIP、IIIP和IVP保护组的APU输入模块失效 M6、M7、M8和M9 IP、IIP、IIIP和IVP通道输入失效 X3 手动停堆开关失效 B1、B2、B3和B4 IP、IIP、IIIP和IVP保护组的PIP失效 M10 处理器失效 X4 背板总线闭锁 C1、C2、C3和C4 IP、IIP、IIIP和IVP保护组的传感器失效 
下载: 导出CSV
表 2 根节点梯形模糊失效率
Table 2. Trapezoidal Fuzzy Failure Rates of Root Nodes
根节点 失效率λ/h−1 X1 (3.15×10−7, 4.28×10−7, 8.76×10−7, 9.89×10−7) X3 (1.62×10−5, 2.16×10−5, 4.32×10−5, 4.86×10−5) X4 (3.64×10−7, 4.87×10−7, 9.82×10−7, 1.11×10−6) X5 (9.37×10−6, 1.25×10−5, 2.50×10−5, 2.81×10−5) X6和X7 (3.20×10−7, 4.30×10−7, 8.70×10−7, 9.80×10−7) X8、C1、C2、C3和C4 (4.13×10−7, 5.57×10−7, 1.13×10−6, 1.28×10−6) X9和X10 (2.04×10−7, 2.73×10−7, 5.50×10−7, 6.19×10−7) A1、A2、A3和A4 (9.36×10−7, 1.24×10−6, 2.43×10−6, 2.73×10−6) B1、B2、B3和B4 (5.87×10−7, 7.84×10−7, 1.57×10−7, 1.76×10−6)
下载: 导出CSV
表 3 根节点的重要度
Table 3. Importance Degrees for Root Nodes
根节点 概率重要度 结构重要度 临界重要度 X1 9.81×10−1 2.59×10−1 7.27×10−2 X2 2.58×10−1 2.47×10−1 1.03×10−2 X3 2.76×10−1 2.47×10−1 9.30×10−1 X4 4.91×10−2 9.21×10−3 2.59×10−3 X5 6.78×10−2 9.21×10−3 9.37×10−1 X6 1.06×10−6 3.07×10−3 3.46×10−7 X7 3.20×10−4 3.07×10−3 3.46×10−7 X8 3.50×10−8 1.84×10−3 2.13×10−9 X9 5.96×10−5 5.53×10−3 2.15×10−9 X10 3.50×10−8 1.84×10−3 1.18×10−15 A1、A2、A3和A4 3.47×10−4 4.06×10−3 7.21×10−5 B1、B2、B3和B4 3.46×10−4 4.06×10−3 2.92×10−5 C1、C2、C3和C4 3.46×10−4 4.06×10−3 2.10×10−5
下载: 导出CSV
-
[1] 肖鹏,周继翔,刘宏春. 反应堆保护系统结构与可靠性的关系[J]. 核动力工程,2013, 34(S1): 179-183. [2] 周海翔,王卫国. 田湾核电站数字化反应堆保护系统可靠性分析[J]. 核电子学与探测技术,2009, 29(6): 1272-1276,1281. doi: 10.3969/j.issn.0258-0934.2009.06.006 [3] 刘华,韩文兴,阳小华,等. 多方法融合的反应堆紧急停堆子系统安全性分析[J]. 核动力工程,2018, 39(3): 156-161. doi: 10.13832/j.jnpe.2018.03.0156 [4] FAHMY R A. Development of dynamic fault tree model for reactor protection system[J]. Process Safety Progress, 2021, 40(2): e12201. [5] MUTA H, MURAMATSU K. Quantitative modeling of digital reactor protection system using Markov state-transition model[J]. Journal of Nuclear Science and Technology, 2014, 51(9): 1073-1086. doi: 10.1080/00223131.2014.906331 [6] MARQUEZ D, NEIL M, FENTON N. Improved reliability modeling using Bayesian networks and dynamic discretization[J]. Reliability Engineering & System Safety, 2010, 95(4): 412-425. [7] SHI Q P, KANG J, WANG R, et al. A framework of intrusion detection system based on Bayesian network in IoT[J]. International Journal of Performability Engineering, 2018, 14(10): 2280-2288. [8] GUO X X, JI J, KHAN F, et al. A novel fuzzy dynamic Bayesian network for dynamic risk assessment and uncertainty propagation quantification in uncertainty environment[J]. Safety Science, 2021, 141: 105285. doi: 10.1016/j.ssci.2021.105285 [9] 吕婷,杨涛,韩宾,等. 基于模糊贝叶斯网络的堆垛机系统可靠性分析[J]. 计算机应用研究,2014, 31(12): 3632-3636. doi: 10.3969/j.issn.1001-3695.2014.12.030 [10] 李成豪,王淳,尹发根,等. 含潮流路由器的配电网最优潮流计算[J]. 电力系统保护与控制,2019, 47(6): 1-8. [11] 蒋程,王硕,王宝庆,等. 基于拉丁超立方采样的含风电电力系统的概率可靠性评估[J]. 电工技术学报,2016, 31(10): 193-206. doi: 10.3969/j.issn.1000-6753.2016.10.023 [12] 陈鹏,刘宏春,冯威,等. PSA技术在反应堆保护系统设计中的应用[J]. 核标准计量与质量,2019(4): 35-42. doi: 10.3969/j.issn.1673-453X.2019.04.007 [13] 邱敏. 基于动态故障树的列控系统风险分析与控制[D]. 成都: 西南交通大学, 2014. [14] LIANG X F, WANG H D, YI H, et al. Warship reliability evaluation based on dynamic Bayesian networks and numerical simulation[J]. Ocean Engineering, 2017, 136: 129-140. doi: 10.1016/j.oceaneng.2017.03.023 [15] 焦志秀,于龙. 基于动态贝叶斯网络的接触网系统可靠性研究[J]. 铁道科学与工程学报,2021, 18(11): 3040-3047. doi: 10.19713/j.cnki.43-1423/u.T20201146 -
计量
- 文章访问数: 152
- HTML全文浏览量: 24
- PDF下载量: 38
- 被引次数: 0
