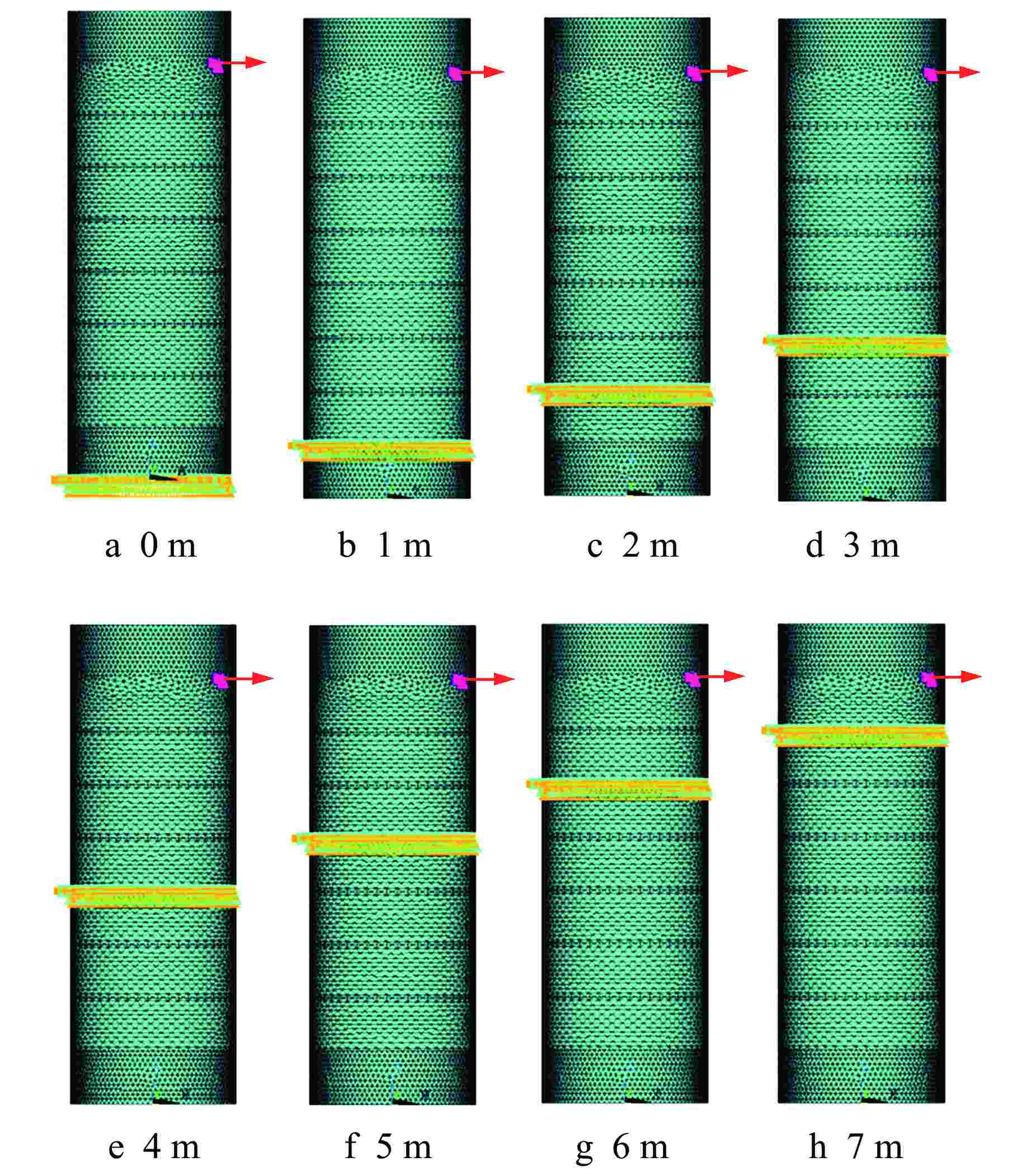
Local Stiffness Calculation and Characteristics Analysis of Cylinder and Lug Connection Structure
-
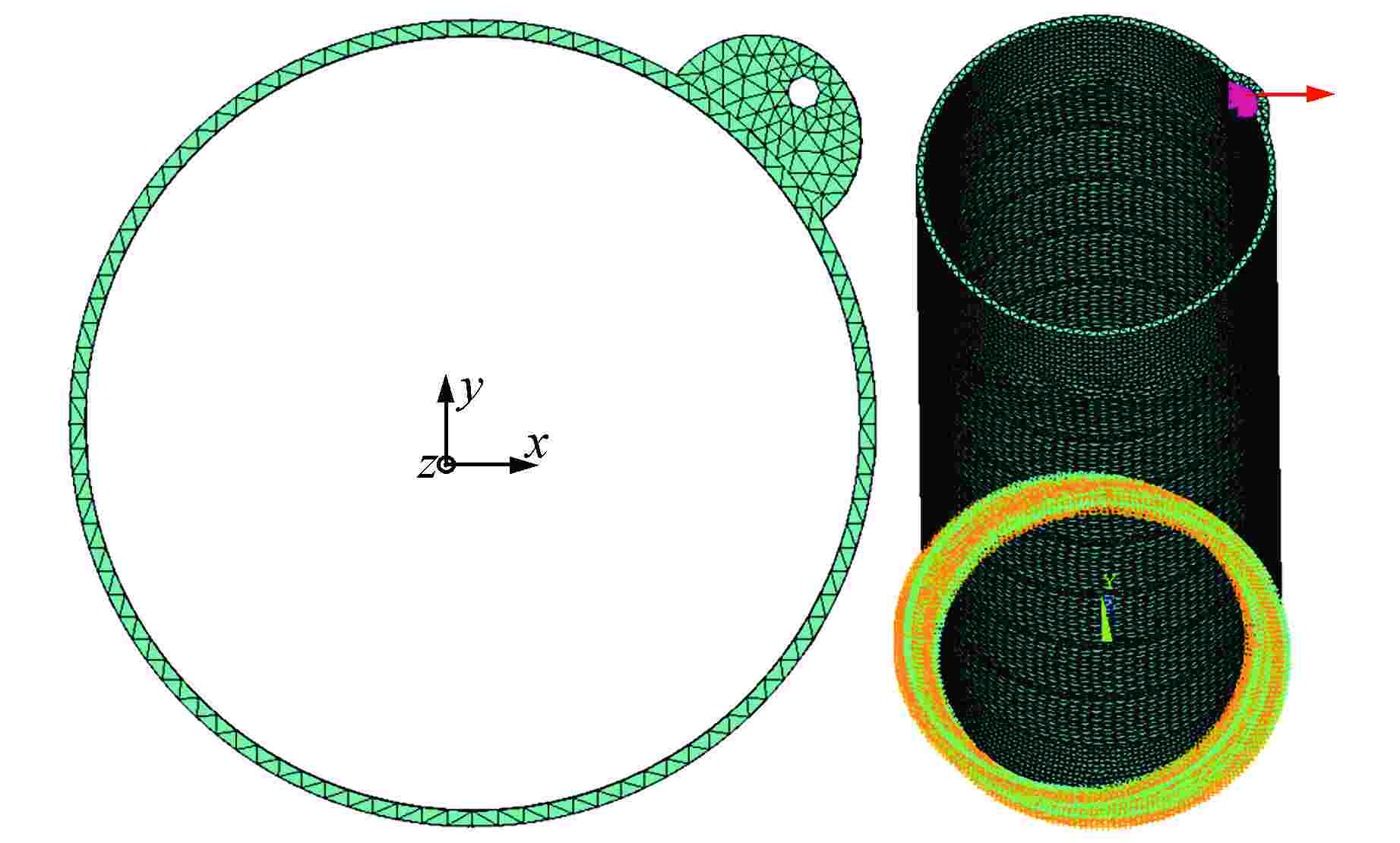
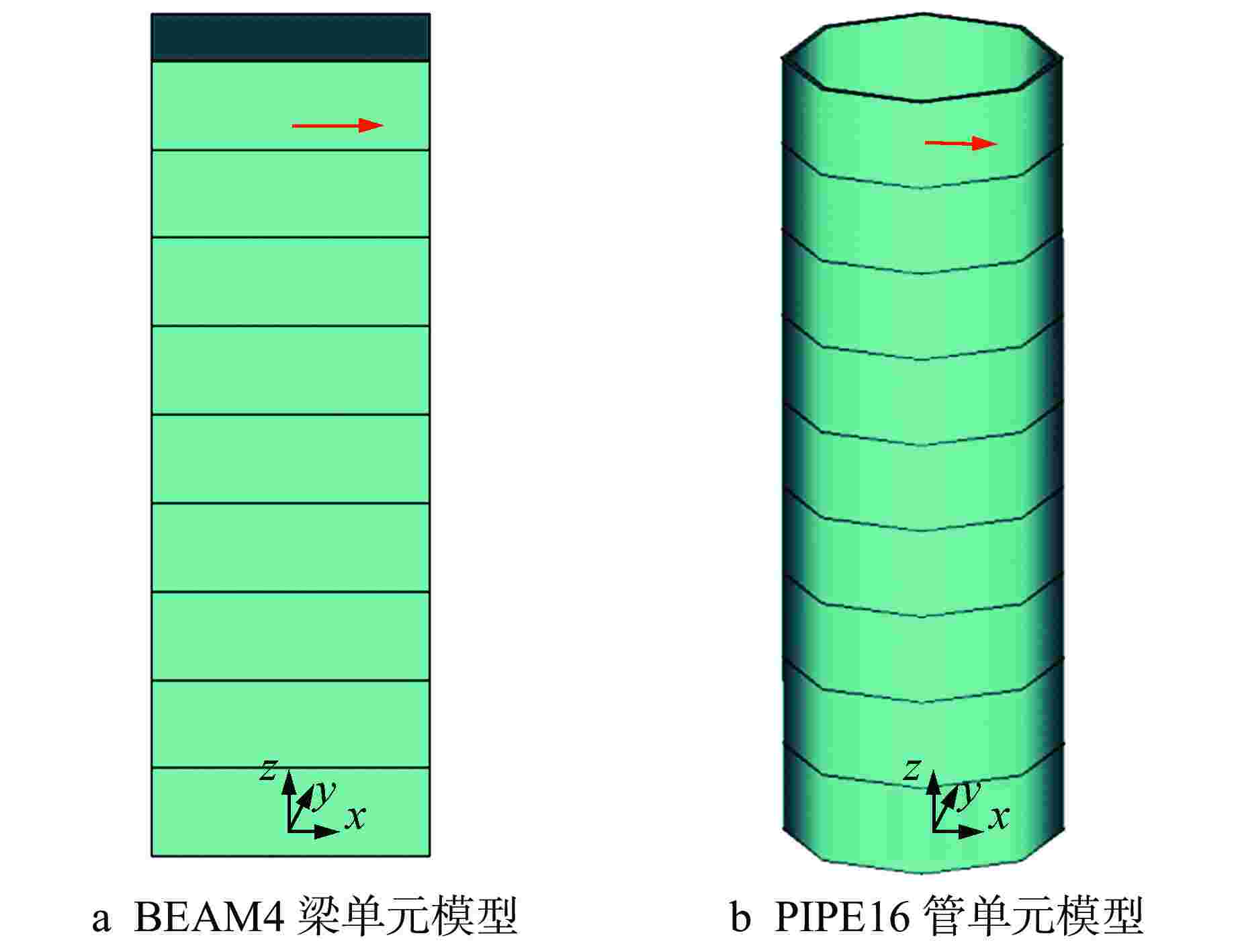
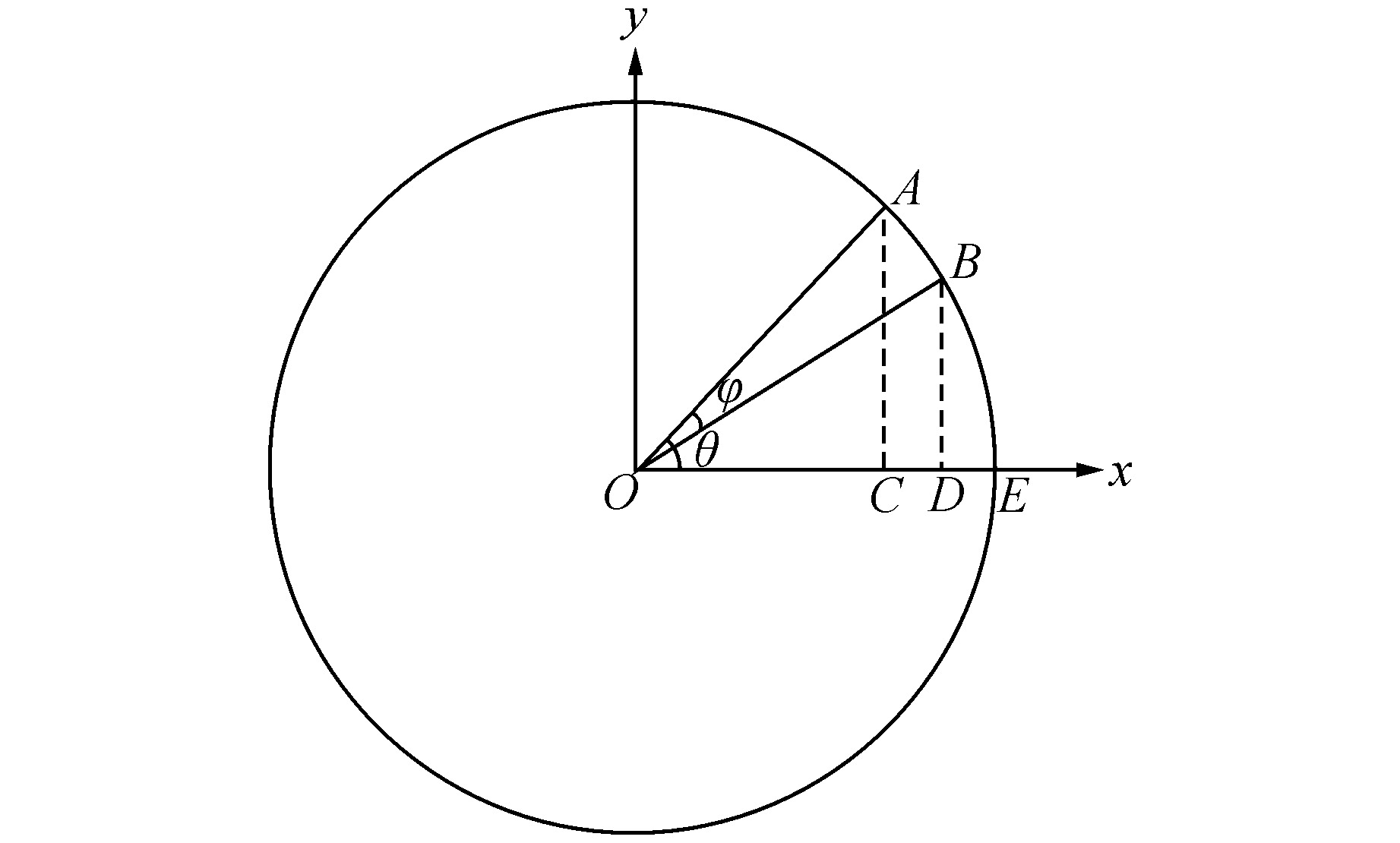
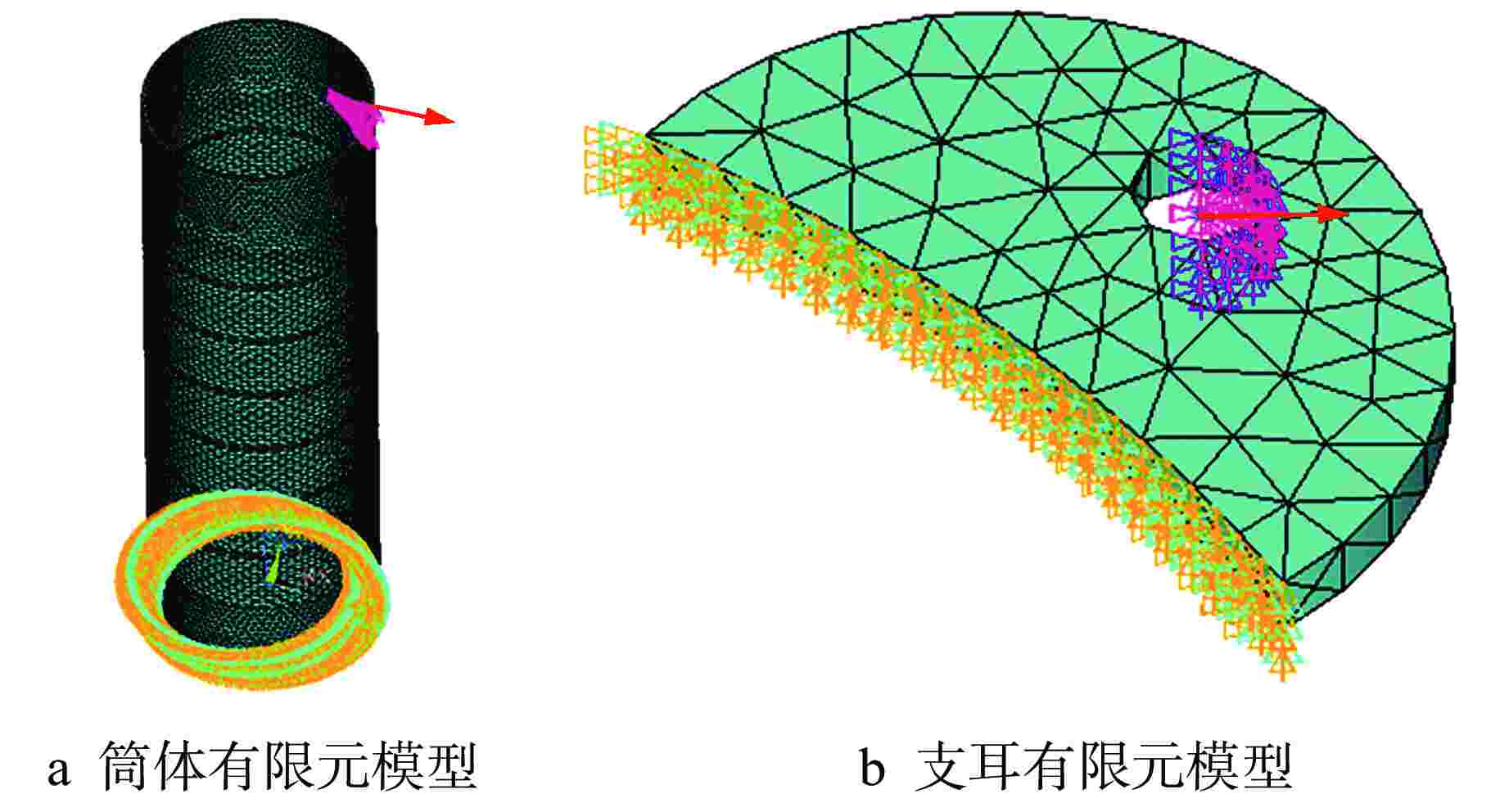
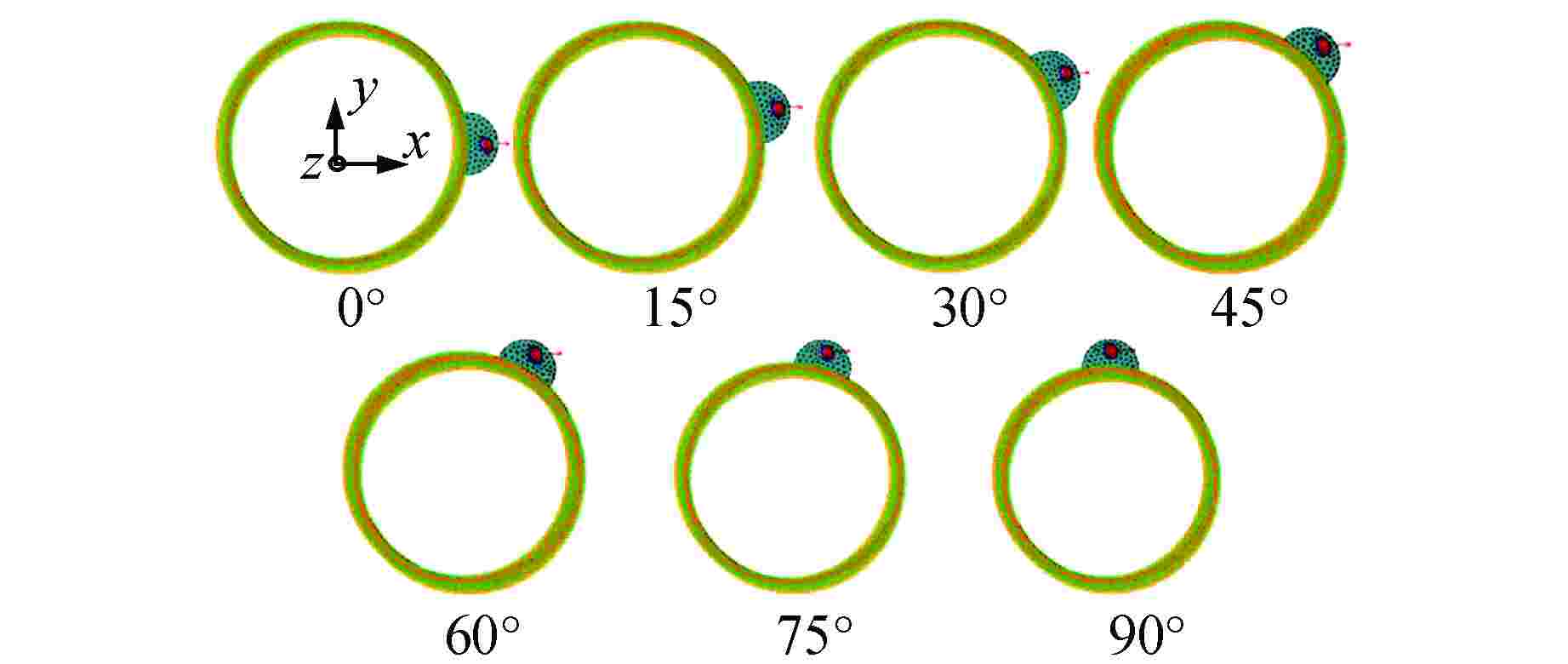
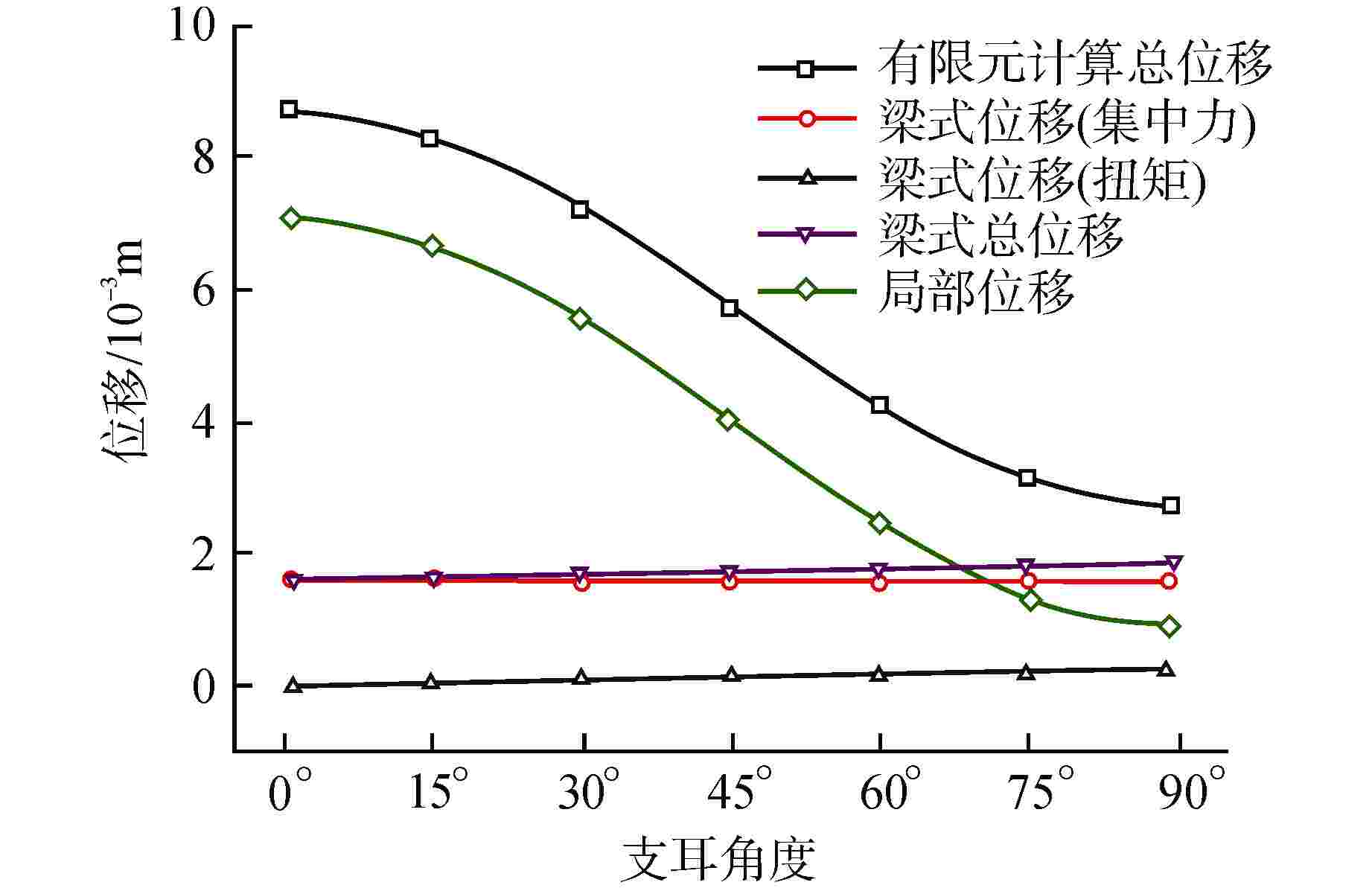
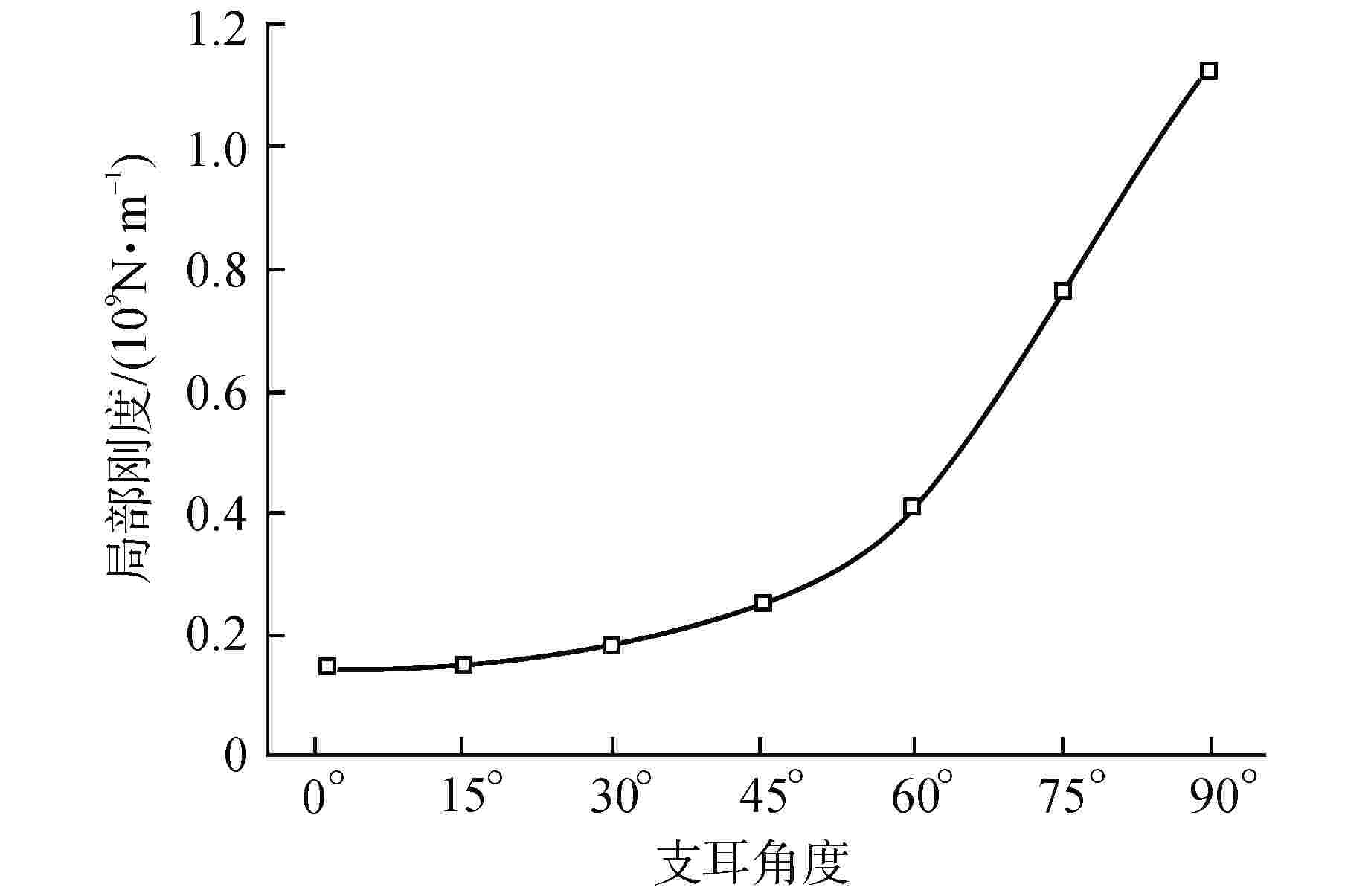
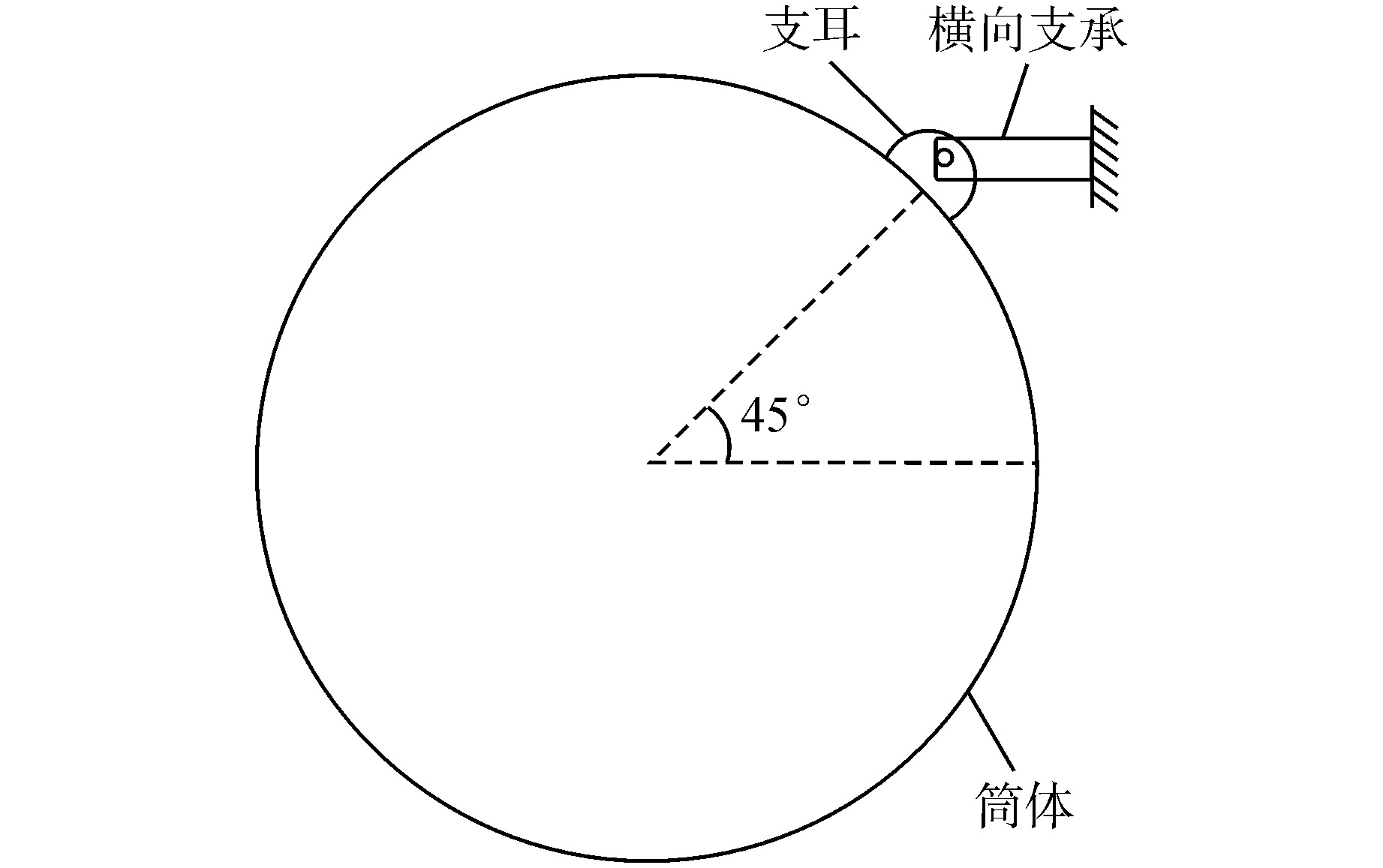
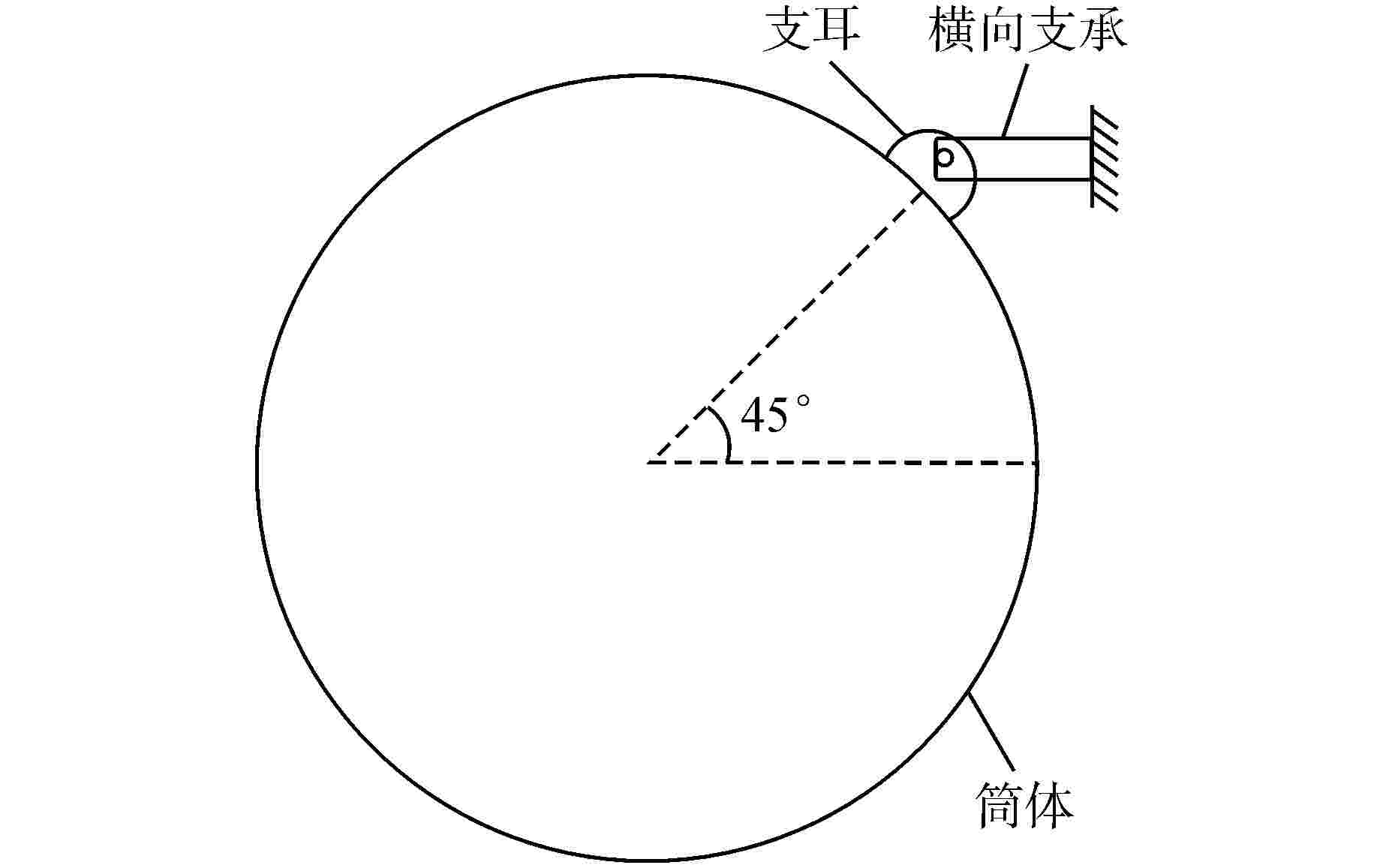
摘要: 核电厂反应堆系统中典型筒体支耳连接结构的局部刚度准确计算具有重要的工程意义。本文建立了筒体支耳连接结构的三维有限元模型，分析得到了有限元计算总位移，并给出由集中力和扭矩分别引起的梁式位移计算方法，从而求解梁式总位移，进而得到筒体支耳连接结构的局部刚度。通过建立筒体支耳连接结构的分解模型进行局部刚度计算，探讨了与整体模型局部刚度计算结果的差异。采用整体模型计算方法，选取不同的边界面进行局部刚度计算，得到了相应的局部刚度变化规律，同时通过调整支耳角度研究其对局部刚度特性的影响。本文研究可为筒体支耳连接结构工程设计提供参考。Abstract: It is of great engineering significance to accurately calculate the local stiffness of typical cylinder and lug connection structures in nuclear power plant reactor system. In this paper, a three-dimensional finite element model of cylinder and lug connection structure is established. The total displacement can be acquired by finite element calculation, and the calculation method is respectively introduced to solve the beam displacement due to concentrated force and torque, which will be used to calculate the final local stiffness of cylinder and lug connection structure. The separate model of cylinder and lug connection structure is established, which is also used to calculate the final local stiffness, and the local stiffness difference is discussed by comparing with the calculation results of whole model. The whole model calculation method is considered to calculate the local stiffness by selecting different boundary planes, and the variation law of local stiffness is obtained. At the same time, the angle of lug is adjusted to calculate and study the influence on local stiffness characteristics. This paper can provide reference for engineering design of cylinder and lug connection structure.
-
图 2 筒体支耳连接结构有限元模型
红色箭头指示力载荷方向
Figure 2. Finite Element Model of Cylinder and Lug Connection Structure
图 6 不同距离下的筒体支耳连接结构有限元模型
Figure 6. Finite Element Model of Cylinder and Lug Connection Structure under Different Distance
图 9 不同支耳角度下的筒体支耳连接结构有限元模型
Figure 9. Finite Element Model of Cylinder and Lug Connection Structure under Different Angle of Lug
表 1 局部刚度计算相关结果
Table 1. Related Results of Local Stiffness Calculation
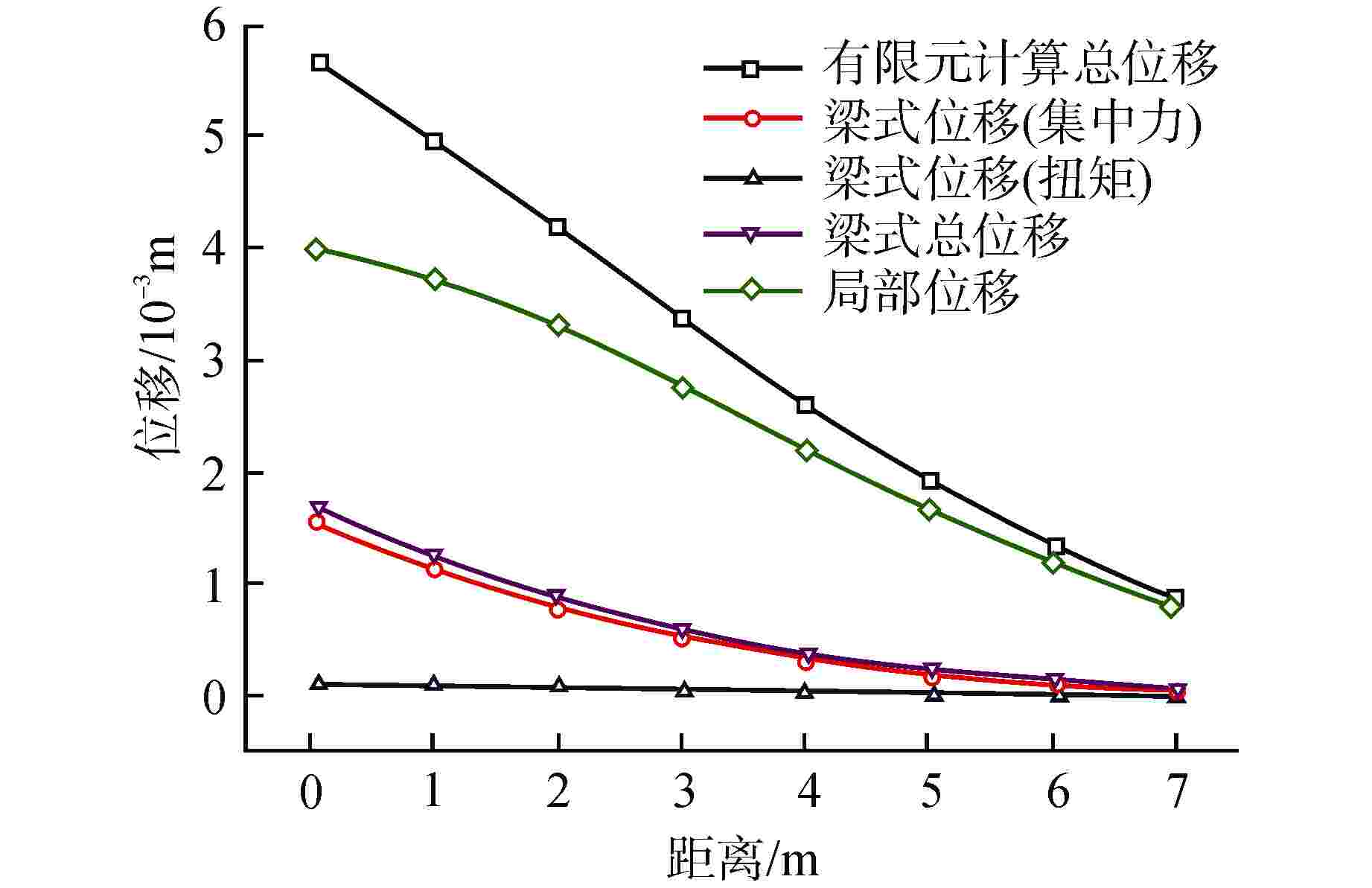
参数 数值 有限元计算总位移/mm 5.716 梁式位移（集中力）/mm 1.592 梁式位移（扭矩）/mm 0.1236 力载荷/N 106 局部刚度/(N·m−1) 2.5×108 
下载: 导出CSV
表 2 不同单元尺寸下的局部刚度
Table 2. Local Stiffness under Different Element Size
筒体模型
网格尺寸/m支耳模型
网格尺寸/m局部刚度/（N·m−1） 0.08 0.08 2.684×108 0.08 0.09 2.684×108 0.08 0.10 2.684×108 0.09 0.08 2.696×108 0.09 0.09 2.695×108 0.09 0.10 2.696×108 0.10 0.08 2.699×108 0.10 0.09 2.699×108 0.10 0.10 2.699×108
下载: 导出CSV
-
[1] 曹庆禺,蒋济同. 混凝土筒体刚度简化计算方法研究[J]. 中国水运,2007, 7(2): 92-93. [2] 耿娜娜,徐培福. 带转换层筒体结构的刚度和剪力分布突变[J]. 建筑科学,2002, 18(3): 6-9,15. [3] 丁红岩,赵将勇,戎贤. 多筒型基础平台结构基础单体刚度分析方法[J]. 地震工程与工程振动,2003, 23(6): 133-137. doi: 10.3969/j.issn.1000-1301.2003.06.021 [4] 张婷,陈五一. 薄壁筒类零件刚度表述模型的研究[J]. 航空制造技术,2010(9): 78-80. [5] 刘胜利,刘小川,崔荣耀,等. 机体连接处局部刚度对轻型飞机起落架摆振稳定性的影响研究[J]. 振动工程学报,2017, 30(2): 249-254. [6] 祁心韵,黄吉锋. 框架剪力墙结构局部刚度变化对层间位移角的影响研究[J]. 建筑科学,2020, 36(S2): 199-205. [7] 赵锡钱,由敬舜. 局部刚度修正的快速算法[J]. 华东交通大学学报,2001, 18(3): 34-36. [8] 武广号,文毅,黄莺,等. 用局部刚度修正法处理结构优化的全局约束问题[J]. 西安交通大学学报,2003, 37(3): 328-330. [9] 谢东武,葛世平,丁文其. 基于局部刚度修正法的盾构隧道下穿历史保护建筑数值模拟分析[J]. 现代隧道技术,2018, 55(3): 121-129. [10] 孙训方, 方孝淑, 关来泰. 材料力学（I）[M]. 第五版. 北京: 高等教育出版社, 2009: 372. -
计量
- 文章访问数: 406
- HTML全文浏览量: 22
- PDF下载量: 87
- 被引次数: 0
