含强吸收体堆芯的各向异性SP<sub>3</sub>两步法计算研究

李云召; 秦浚玮; 夏凡; 吴宏春; 曹良志

doi:10.13832/j.jnpe.2023.06.0009

含强吸收体堆芯的各向异性SP₃两步法计算研究

doi: 10.13832/j.jnpe.2023.06.0009

李云召^1,,
秦浚玮^1,,
夏凡^{1, 2},
吴宏春¹,
曹良志¹

1.
西安交通大学核科学与技术学院，西安，710049
2.
上海核工程研究设计院股份有限公司，上海，200233

基金项目: 国家自然科学基金（11975181）

详细信息

作者简介:
李云召（1984—），男，教授，现主要从事核反应堆物理相关的科研与教学工作，E-mail: yunzhao@xjtu.edu.cn

中图分类号: TL324
计量
- 文章访问数: 91
- HTML全文浏览量: 30
- PDF下载量: 29
- 被引次数: 0
出版历程
- 收稿日期: 2022-12-15
- 修回日期: 2023-02-01
- 网络出版日期: 2023-12-11
- 刊出日期: 2023-12-15

Anisotropic SP₃ Two-Step Method for Reactor Cores with Strong Absorbers

1.
School of Nuclear Science and Technology, Xi’an Jiaotong University, Xi’an, 710049, China
2.
Shanghai Nuclear Engineering Research & Design Institute Co., Ltd., Shanghai, 200233, China

摘要

摘要: 核反应堆堆芯中出现的强吸收体，尤其是可移动的控制棒，会显著增强堆芯内中子角注量率的角度各向异性效应，传统的各向同性SP₃两步法不能进行有效刻画，需要构建各向异性SP₃两步法。本文首先从2个方面研究各向异性效应；推导了各向异性SP₃方程，建立了适用于各向异性SP₃方程的均匀化模型。通过材料试验堆（MTR）对本文方法进行验证与分析。结果表明，本文研究的各向异性SP₃方程及其均匀化方法较之传统计算方法偏差更小，对于有效增殖系数（k_eff）和功率分布改善较为明显。因此，本文研究的各向异性SP₃两步法能够有效处理含强吸收体堆芯问题。
- 强吸收体 /
- 细网均匀化 /
- 各向异性SP₃ /
- 材料试验堆
Abstract: The strong absorber in the core of nuclear reactor, especially the movable control rod, will significantly enhance the angular anisotropy effect of neutron angular fluence in the core. The traditional isotropic SP₃ two-step method cannot capture the feature effectively, therefore, the anisotropic SP₃ two-step method needs to be constructed. Firstly, this paper studies the anisotropic effect from two aspects; the anisotropic SP₃ equation is derived, and a homogenization model suitable for anisotropic SP₃ equation is established. The methodology proposed in this paper was validated and analyzed through the Material Test Reactor (MTR). The results show that the anisotropy SP₃ equation and its homogenization method in this paper have smaller deviation than the traditional calculation method, and the effective multiplication factor (k_eff) and power distribution are obviously improved. Therefore, the anisotropic SP₃ two-step method in this paper can effectively deal with the core problem with strong absorbers.
- Strong absorber /
- Fine-mesh homogenization /
- Anisotropic SP₃ /
- Material Test Reactor

HTML全文

图 1 MTR 多元件问题示意图

Figure 1. Configuration of MTR Multi-Assembly Problem

下载: 全尺寸图片幻灯片

图 2 新型均匀化模型示意图

Figure 2. Schematic Diagram of New Homogenization Model

下载: 全尺寸图片幻灯片

图 3 不同计算方法所得功率分布偏差示意图

Figure 3. Schematic Diagram of Power Distribution Deviation Obtained by Different Calculation Methods

下载: 全尺寸图片幻灯片

图 4 二维MTR问题堆芯及反射层模型示意图

Figure 4. Schematic Diagram of 2D MTR Core and Reflector Model

下载: 全尺寸图片幻灯片

图 5 二维MTR问题燃料元件模型示意图

Figure 5. Fuel Element Model of 2D MTR Problem

下载: 全尺寸图片幻灯片

图 6 二维MTR问题功率分布偏差示意图

Figure 6. Power Distribution Deviation of the 2D MTR Problem　　　　　

下载: 全尺寸图片幻灯片

表 1 不同散射阶数k_eff计算结果及偏差

Table 1. k_eff Results and Deviations of Different Scattering Orders

计算方式	不插控制棒		Ag-In-Cd控制棒		Hf控制棒		B₄C控制棒
计算方式	k_eff	偏差/pcm	k_eff	偏差/pcm	k_eff	偏差/pcm	k_eff	偏差/pcm
参考解	1.52785	—	0.84798	—	0.83830	—	0.72975	—
Inflow	1.52755	–30	0.85518	+720	0.84516	+686	0.74195	+1220
P₁	1.52829	+44	0.84343	–455	0.83226	–604	0.72414	–561
P₂	1.52834	+49	0.84806	+8	0.83732	–98	0.73081	+106
P₃	1.52832	+47	0.84789	–9	0.83719	–111	0.73087	+112

下载: 导出CSV

表 2 MTR中2种燃料元件的几何与材料信息

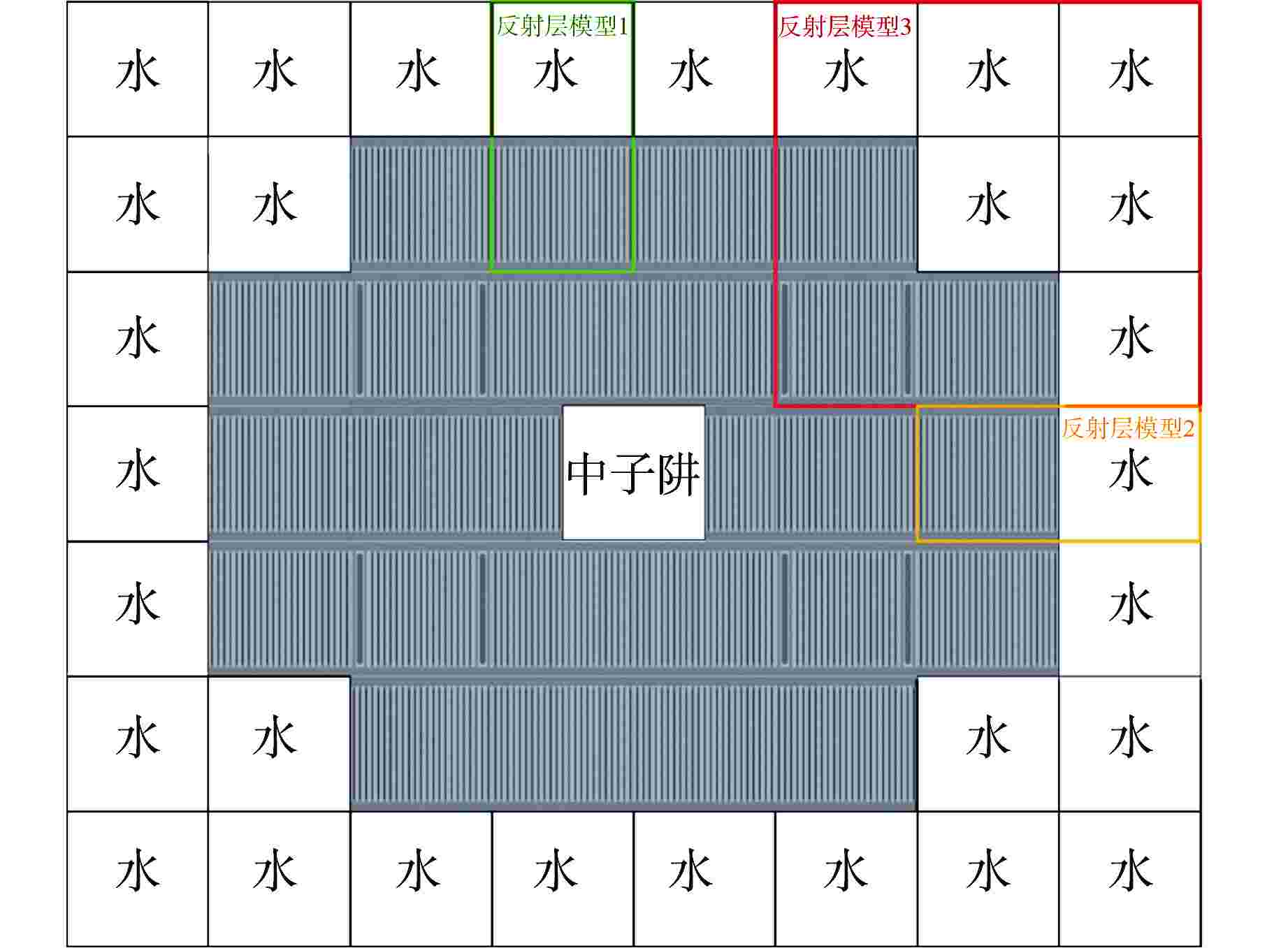
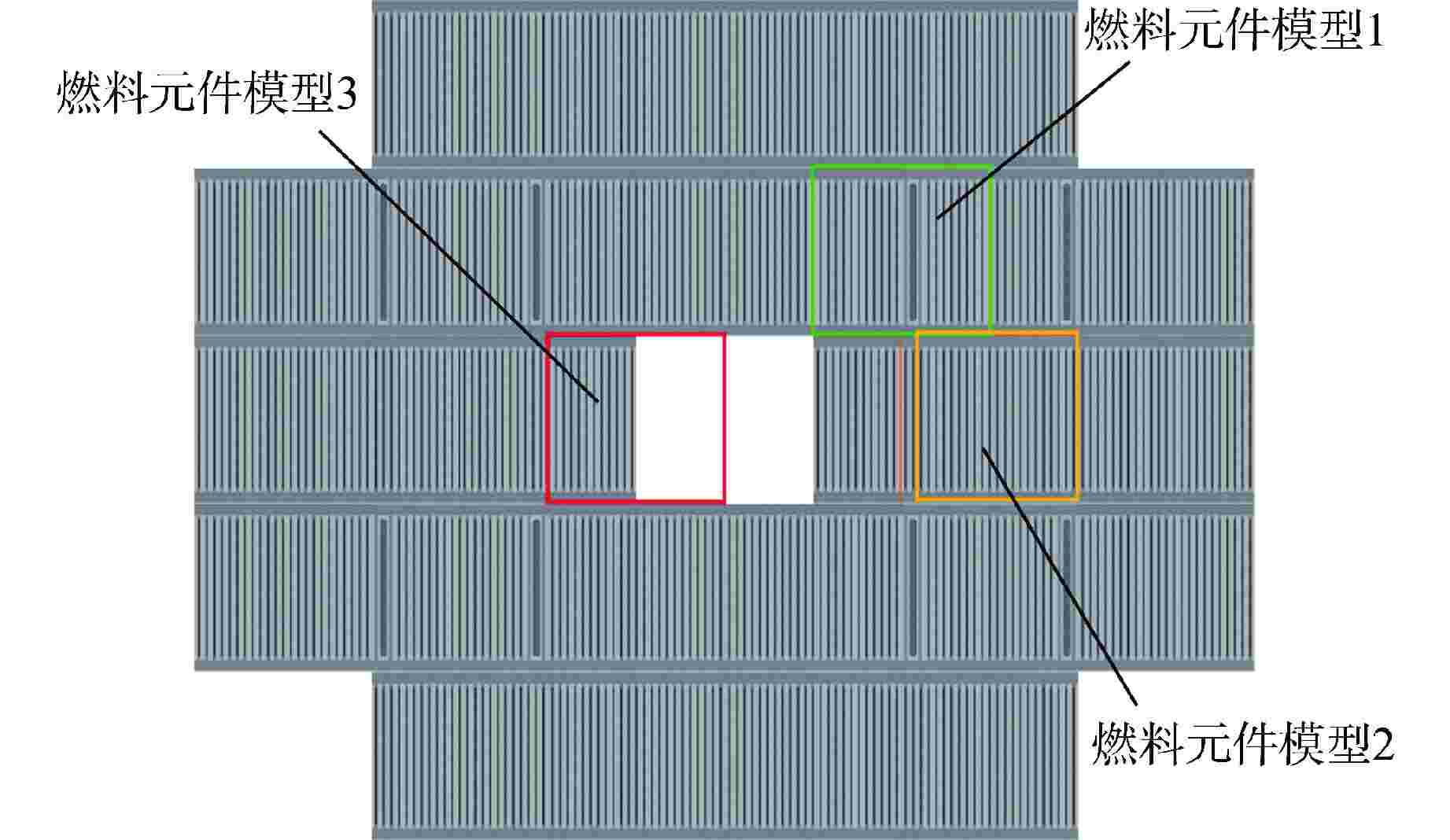
Table 2. Geometric and Material Parameters of 2 Fuel Elements in MTR

参数名称		标准燃料元件	控制燃料元件
组件尺寸/cm		7.7×8.1	7.7×8.1
燃料材料		UAl_x-Al	UAl_x-Al
燃料富集度/%	LEU	20	20
	MEU	45	45
	HEU	93	93
燃料板数		23	17
燃料板厚度/cm		0.051	0.051
燃料板长度/cm		6.3	6.3
包壳材料		Al	Al
包壳厚度/cm		0.038	0.038
板间厚度/cm		0.223	0.223
控制棒材料		—	Ag-In-Cd
LEU—低浓铀；MEU—中浓铀；HEU—高浓铀

下载: 导出CSV

表 3 新型均匀化模型计算结果

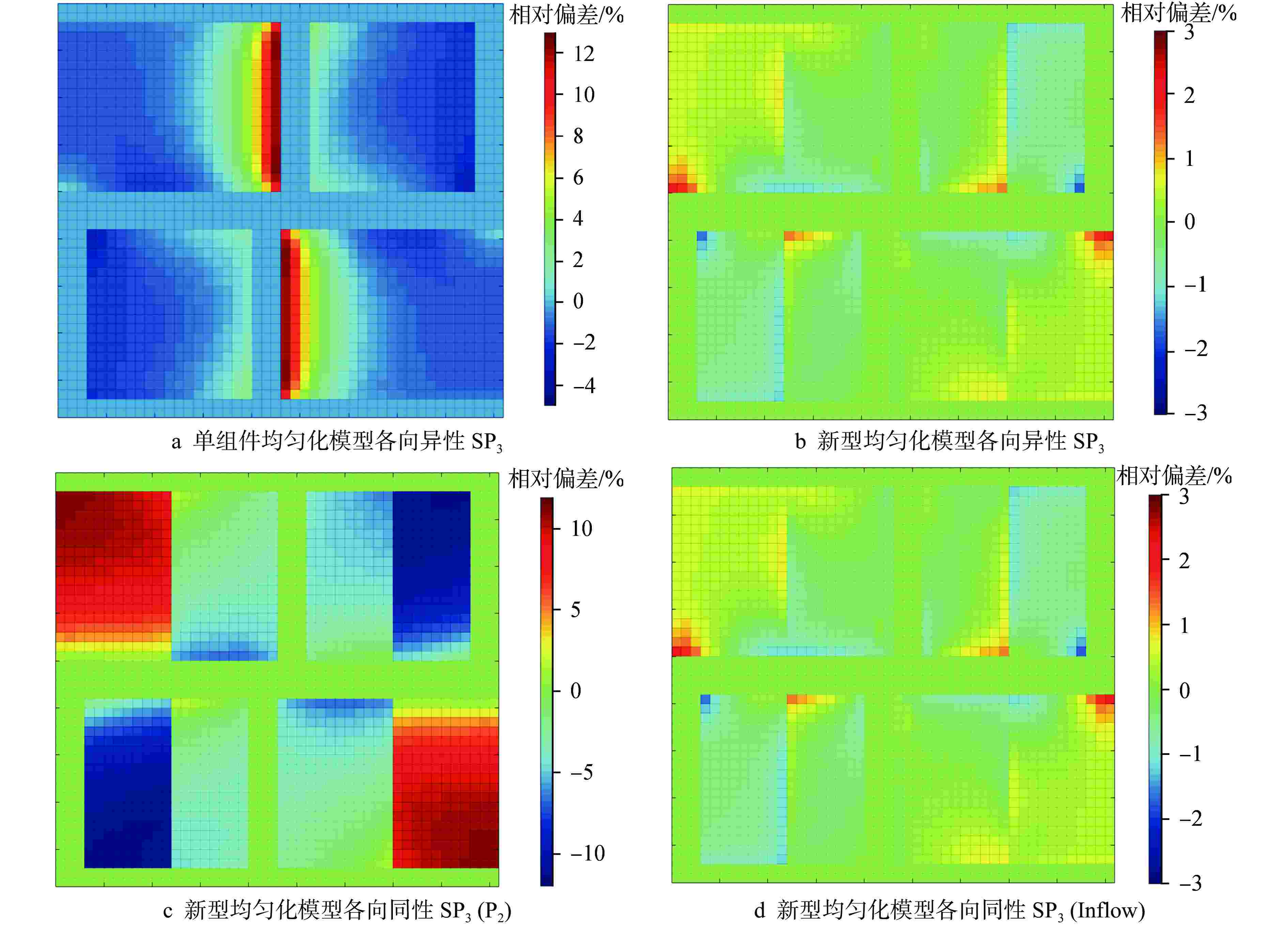
Table 3. Calculation Results of New Homogenization Model

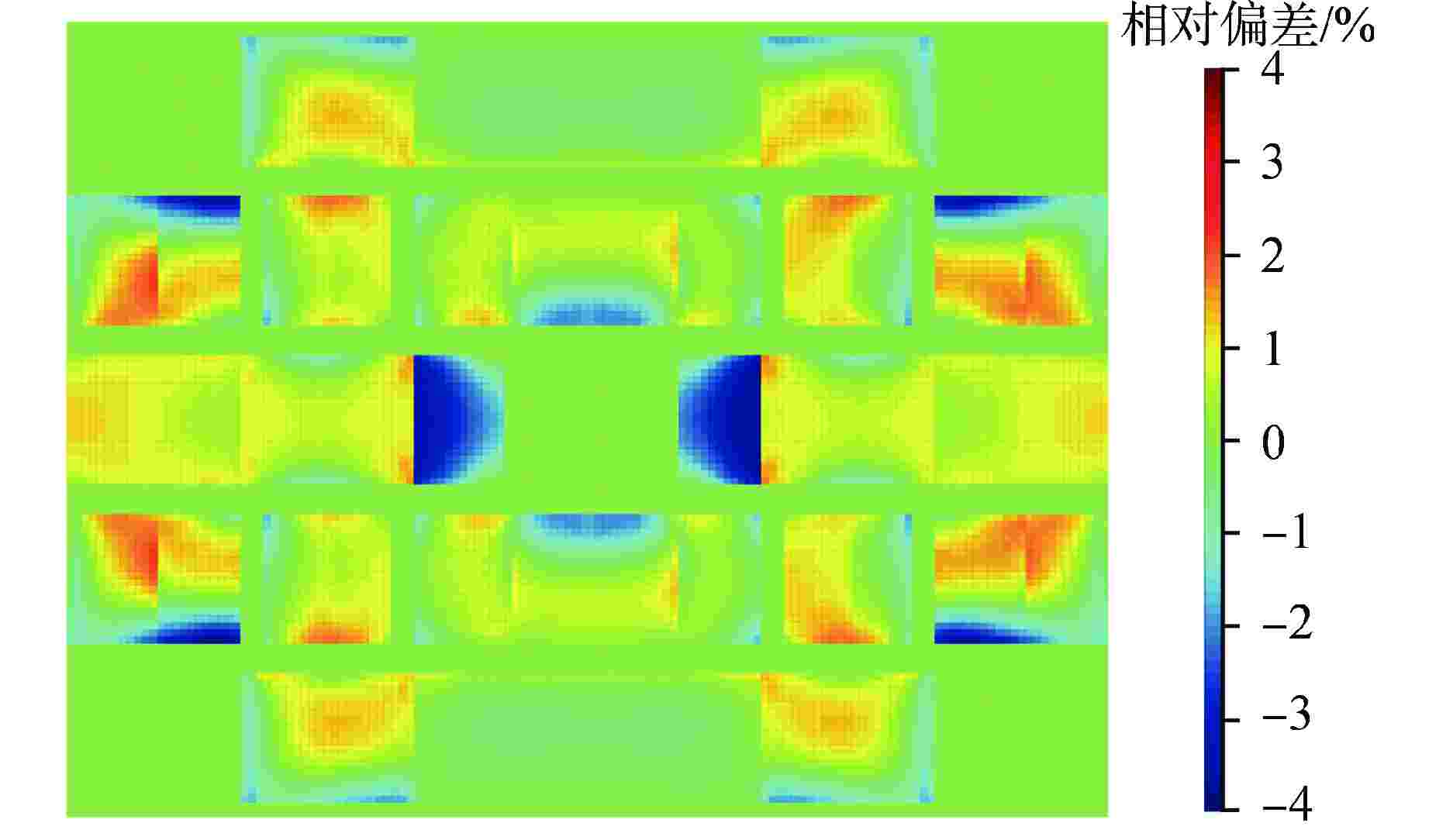
计算方式	参考解	k_eff	k_eff偏差/ pcm	均方根偏差/%	最大偏差/%
各向异性SP₃(P₂)	1.05931	1.05979	+48	0.47	2.10
各向同性SP₃(P₂)		1.07745	+1814	6.92	−11.46
各向同性SP₃(Inflow)		1.05702	−229	0.66	2.64

下载: 导出CSV

表 4 二维MTR堆芯问题计算结果

Table 4. Results of 2D MTR Core Problem

k_eff			功率分布偏差/%
参考值	计算值	偏差/pcm	均方根	最大值
1.01545	1.01616	+71	0.97	3.72

下载: 导出CSV

参考文献(22)

[1]	PALMTAG S P. Advanced nodal methods for MOX fuel analysis[D]. Cambridge: Massachusetts Institute of Technology, 1997.
[2]	TATSUMI M, YAMAMOTO A. Advanced PWR core calculation based on multi-group nodal-transport method in three-dimensional pin-by-pin geometry[J]. Journal of Nuclear Science and Technology, 2003, 40(6): 376-387. doi: 10.1080/18811248.2003.9715369
[3]	YANG W, ZHENG Y Q, WU H C, et al. High-performance whole core pin-by-pin calculation based on EFEN-SP₃ method[J]. Nuclear Power Engineering, 2014, 35(5): 164-167.
[4]	TATSUMI M, OHOKA Y, ENDO T, et al. Verification and validation of AEGIS/SCOPE2: the state-of-the-art in-core fuel management system for PWRs[C]//18th International Conference on Nuclear Engineering. Xi’an: American Society of Mechanical Engineers, 2010,doi: 10.1115/ICONE18-29154.
[5]	GRUNDMANN U, MITTAG S. Super-homogenisation factors in pinwise calculations by the reactor dynamics code DYN3D[J]. Annals of Nuclear Energy, 2011, 38(10): 2111-2119. doi: 10.1016/j.anucene.2011.06.030
[6]	LIU S C, WANG G B, LIANG J G, et al. Burnup-dependent core neutronics analysis of plate-type research reactor using deterministic and stochastic methods[J]. Annals of Nuclear Energy, 2015, 85: 830-836. doi: 10.1016/j.anucene.2015.06.041
[7]	MARLEAU G, HÉBERT A, ROY R. A user guide for DRAGON version DRAGON_000331 Realease 3.04, IGE-174[Z]. 2000
[8]	HÉBERT A, SEKKI D, CHAMBON R. A user guide for DONJON version4: IGE-300[R]. Montréal: École Polytechnique de Montréal, 2013.
[9]	MA J M, WANG G B, YUAN S, et al. An improved assembly homogenization approach for plate-type research reactor[J]. Annals of Nuclear Energy, 2015, 85: 1003-1013. doi: 10.1016/j.anucene.2015.07.018
[10]	汤春桃. 中子输运方程特征线解法及嵌入式组件均匀化方法的研究[D]. 上海: 上海交通大学, 2009.
[11]	CHAUDRI K S, MIRZA S M. Burnup dependent Monte Carlo neutron physics calculations of IAEA MTR benchmark[J]. Progress in Nuclear Energy, 2015, 81: 43-52. doi: 10.1016/j.pnucene.2014.12.018
[12]	SHAABAN I, ALBARHOUM M. Performance of the MTR core with MOX fuel using the MCNP4C2 code[J]. Applied Radiation and Isotopes, 2016, 114: 92-103. doi: 10.1016/j.apradiso.2016.05.009
[13]	ALAWNEH L M, PARK C J, JARADAT M K, et al. Burnup estimation for plate type fuel assembly of research reactors through the least square fitting method[J]. Annals of Nuclear Energy, 2014, 71: 37-45. doi: 10.1016/j.anucene.2014.03.029
[14]	MARGULIS M, GILAD E. Monte Carlo and nodal neutron physics calculations of the IAEA MTR benchmark using Serpent/DYN3D code system[J]. Progress in Nuclear Energy, 2016, 88: 118-133. doi: 10.1016/j.pnucene.2015.12.008
[15]	YAMAMOTO A, KITAMURA Y, YAMANE Y. Simplified treatments of anisotropic scattering in LWR core calculations[J]. Journal of Nuclear Science and Technology, 2008, 45(3): 217-229. doi: 10.1080/18811248.2008.9711430
[16]	XIA F, ZU T J, WU H C. Effect and treatment of angular dependency of multi-group total cross section and anisotropic scattering in fine-mesh transport calculation[J]. Annals of Nuclear Energy, 2018, 114: 110-121. doi: 10.1016/j.anucene.2017.11.049
[17]	USHIO T, TAKEDA T, MORI M. Neutron anisotropic scattering effect in heterogeneous cell calculations of light water reactors[J]. Journal of Nuclear Science and Technology, 2003, 40(7): 464-480. doi: 10.1080/18811248.2003.9715381
[18]	GELBARD E M. Application of spherical harmonics method to reactor problems: WAPD-T-1182[R]. West Mifflin: Bettis Atomic Power Laboratory, 1960
[19]	NELSON A. Improved convergence rate of multi-group scattering moment tallies for Monte Carlo neutron transport codes[D]. Michigan: University of Michigan, 2014.
[20]	WANG S C, CAO L Z, LI Y Z, et al. An energy-group structure optimization from seven to four for PWR-core pin-by-pin calculation[J]. Nuclear Engineering and Design, 2023, 402: 112115. doi: 10.1016/j.nucengdes.2022.112115
[21]	IAEA. Research reactor core conversion from the use of highly enriched uranium fuels: guidebook[M]. Vienna: International Atomic Energy Agency, 1980: 39-45.
[22]	LI Y Z, ZHANG B, HE Q M, et al. Development and verification of PWR-core fuel management calculation code system NECP-bamboo: part I bamboo-lattice[J]. Nuclear Engineering and Design, 2018, 335: 432-440. doi: 10.1016/j.nucengdes.2018.05.030