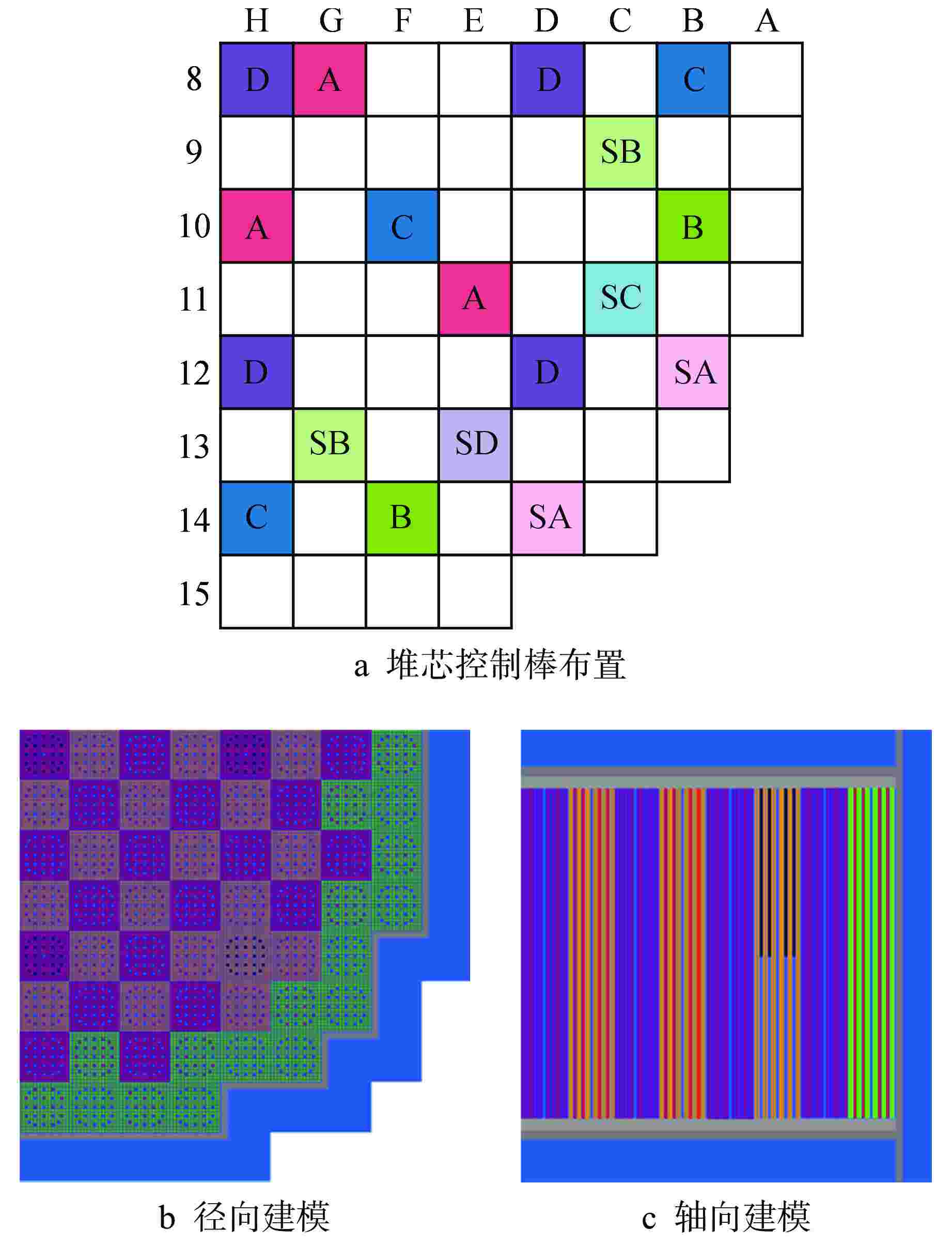
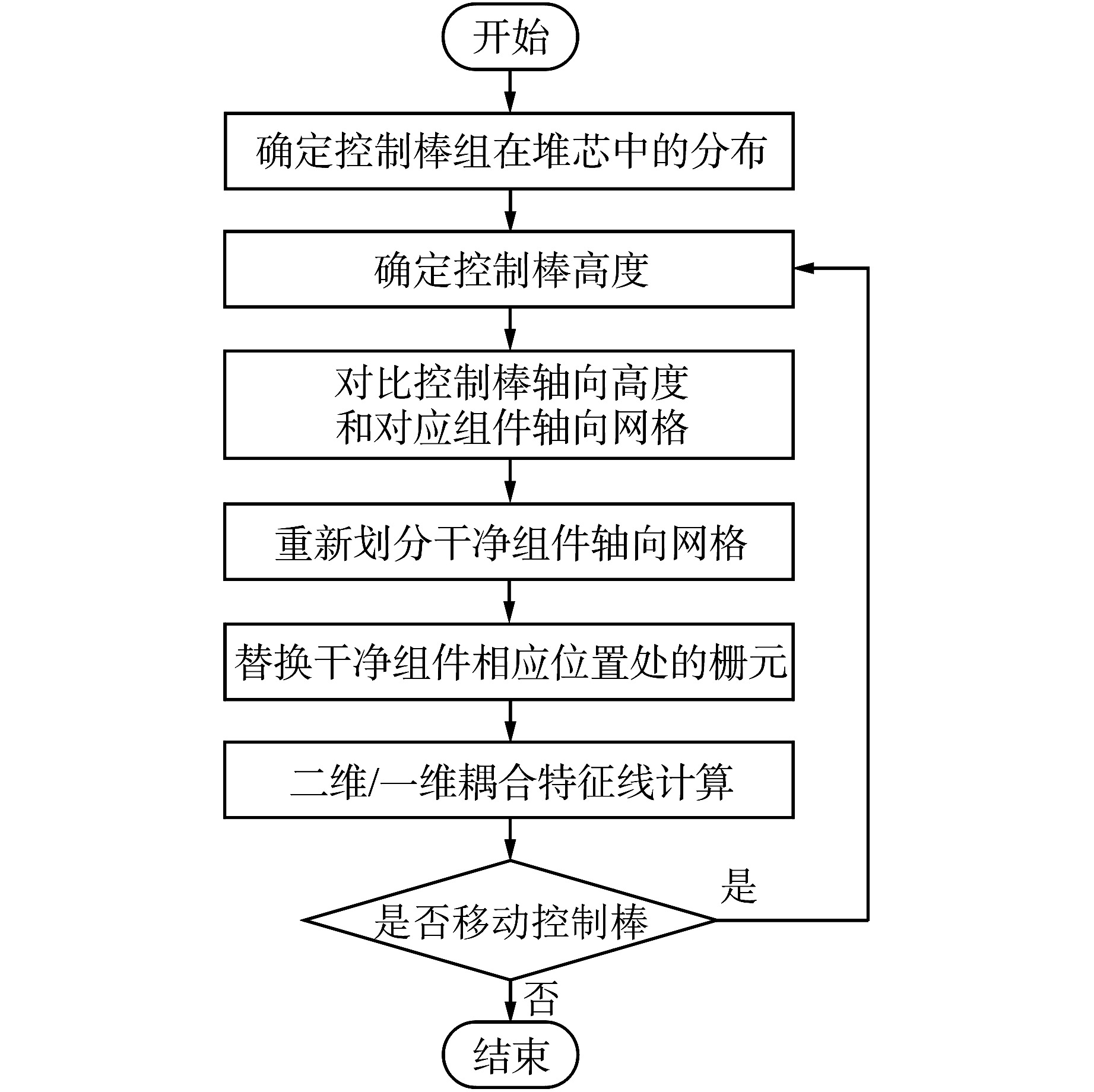
Treatment Method of Control Rod Cusping Effect in 2D/1D Coupled Characteristics Transport Calculation
-
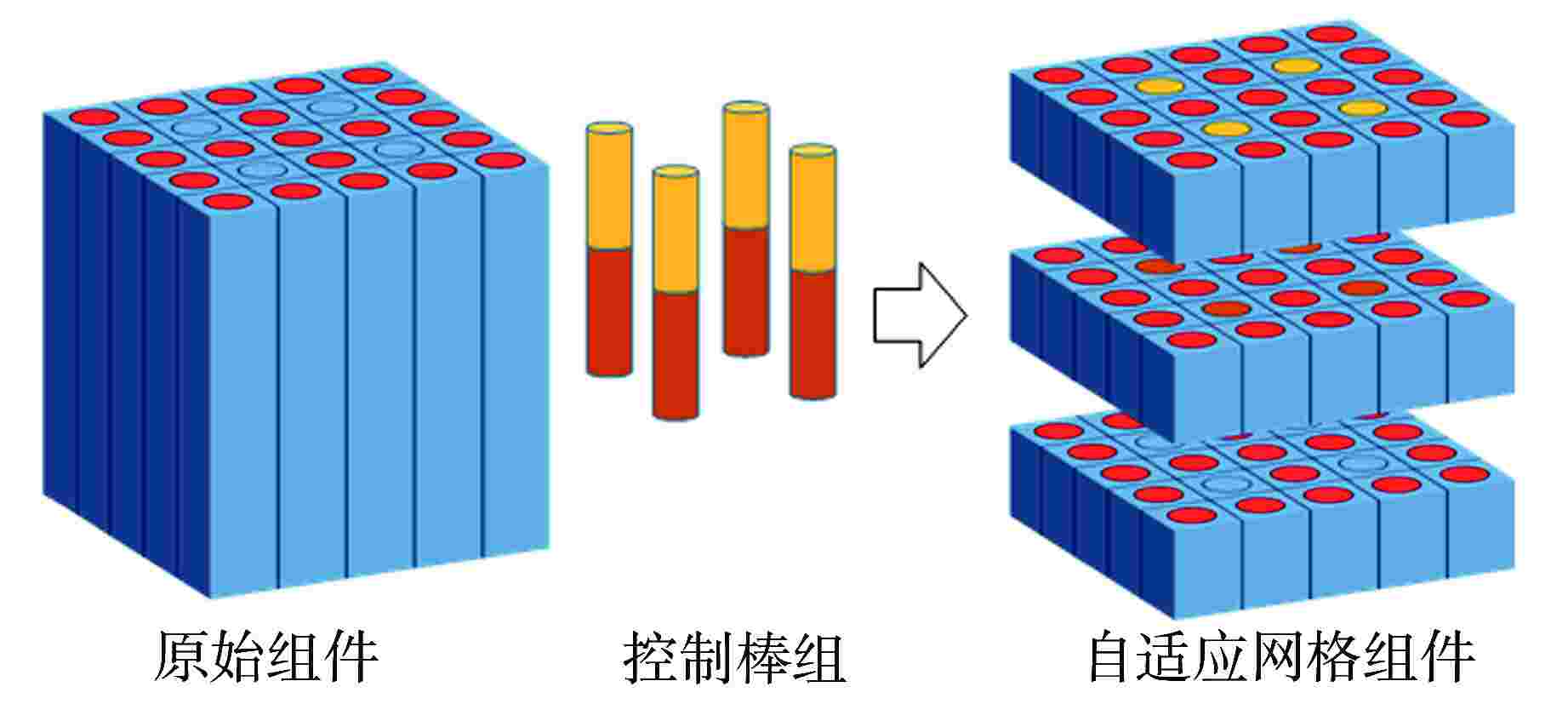
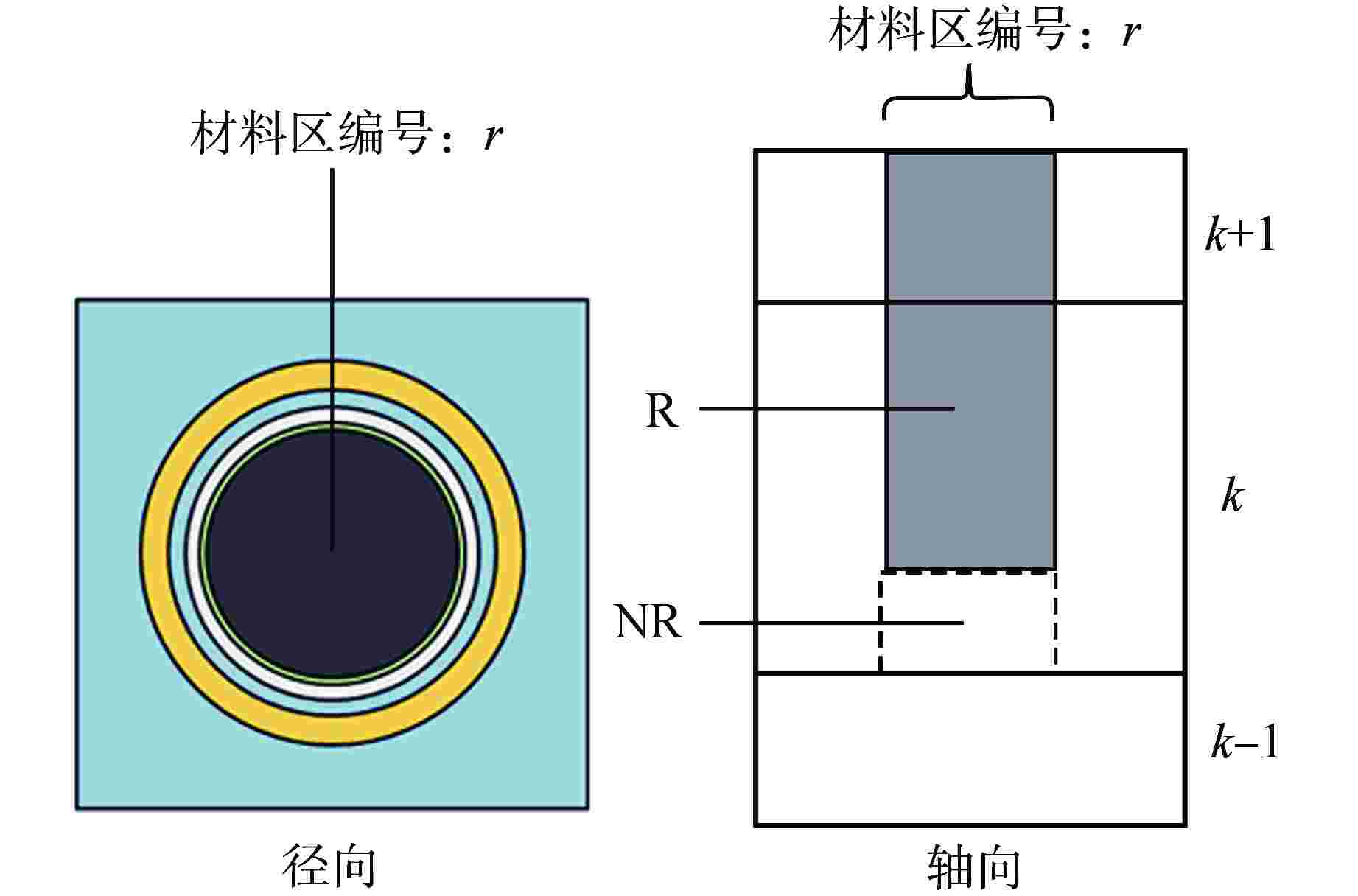
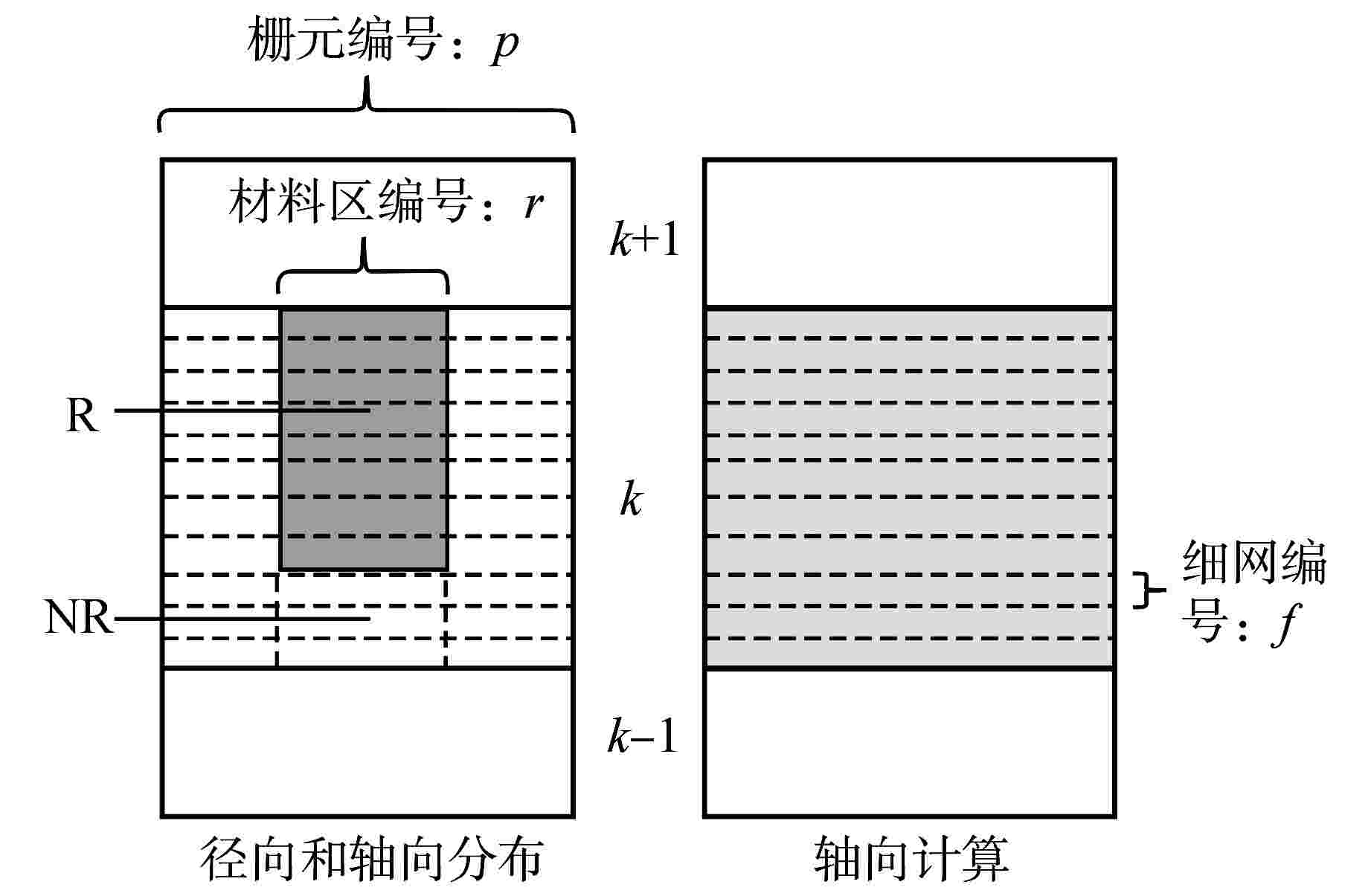
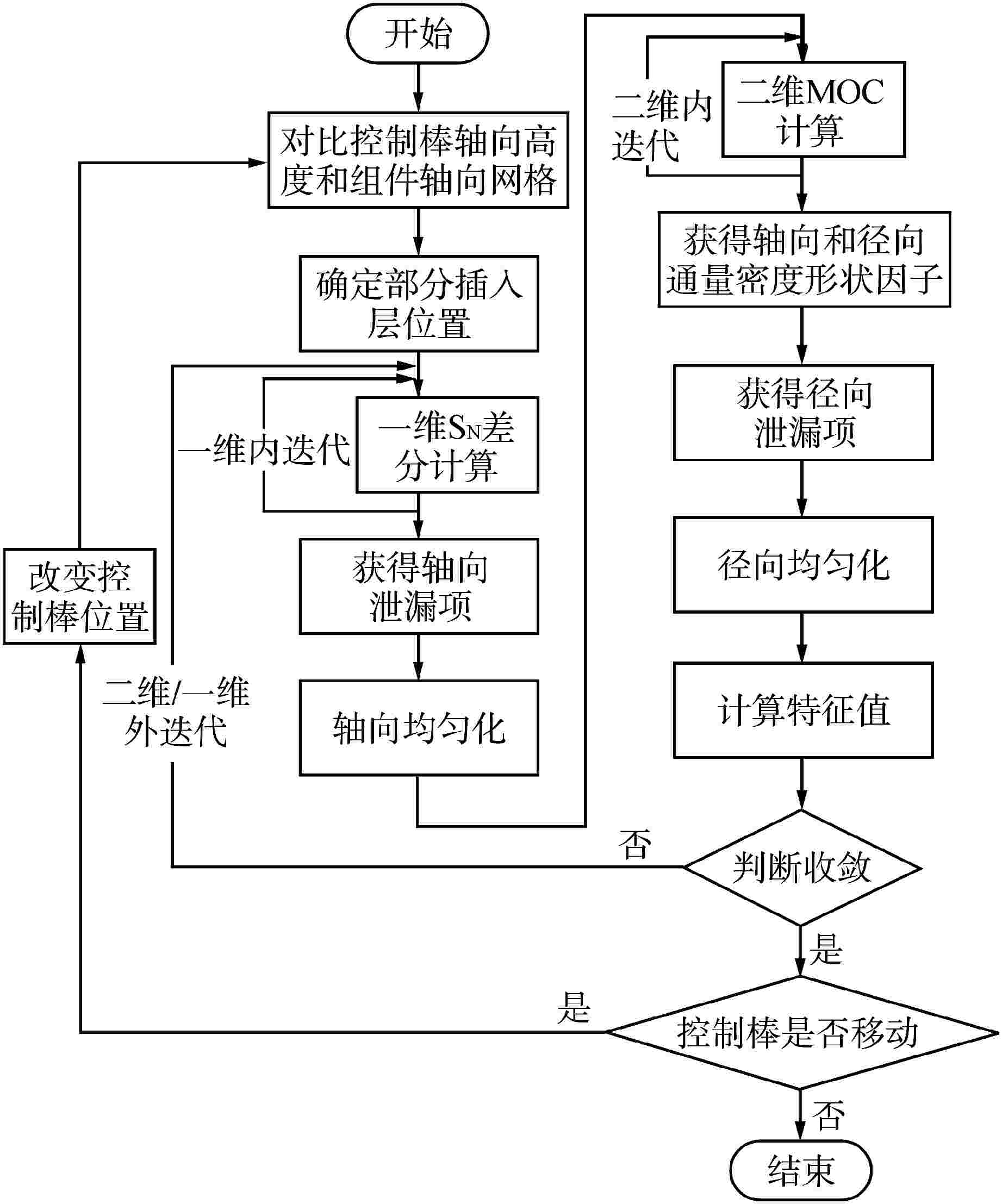
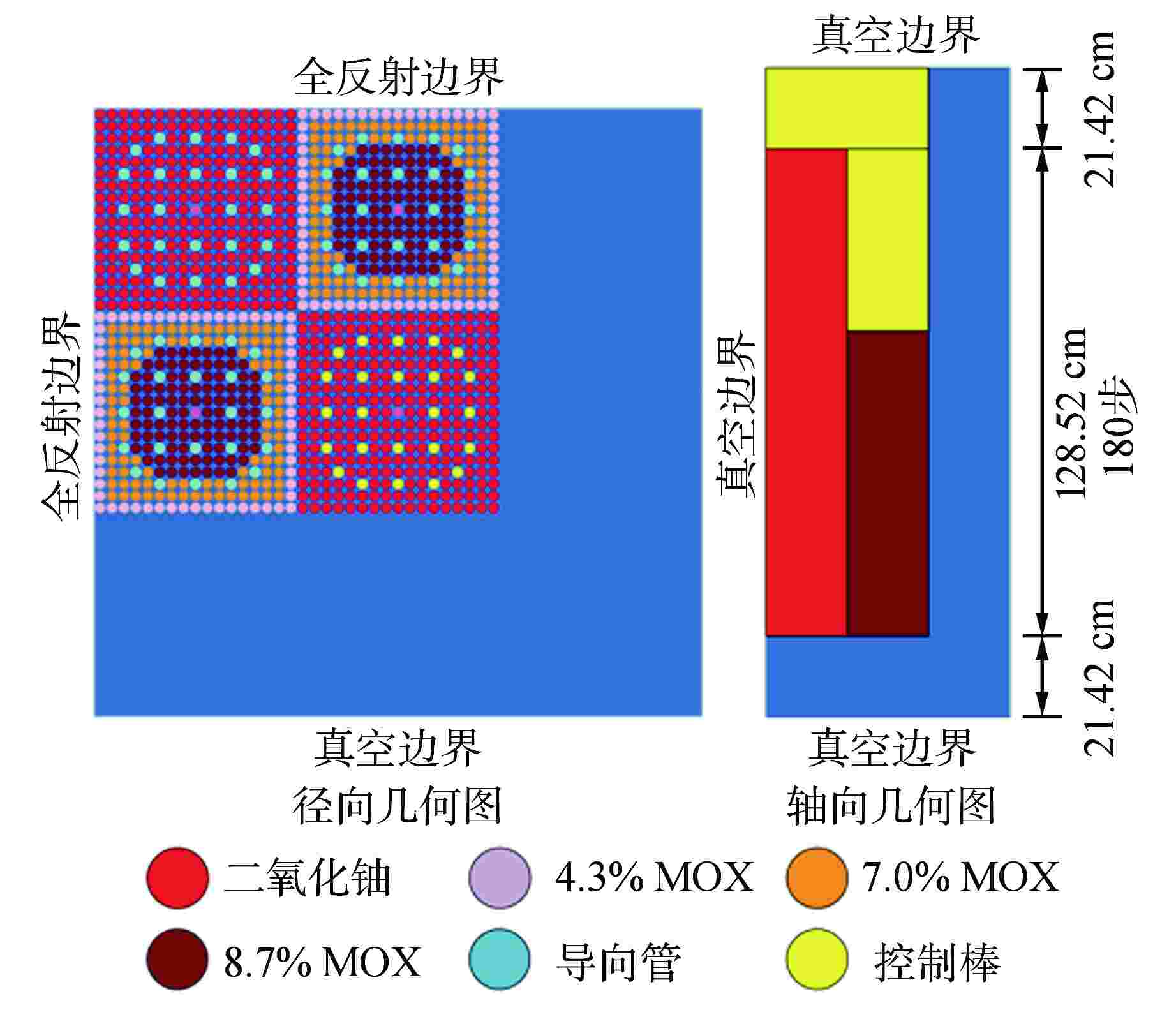
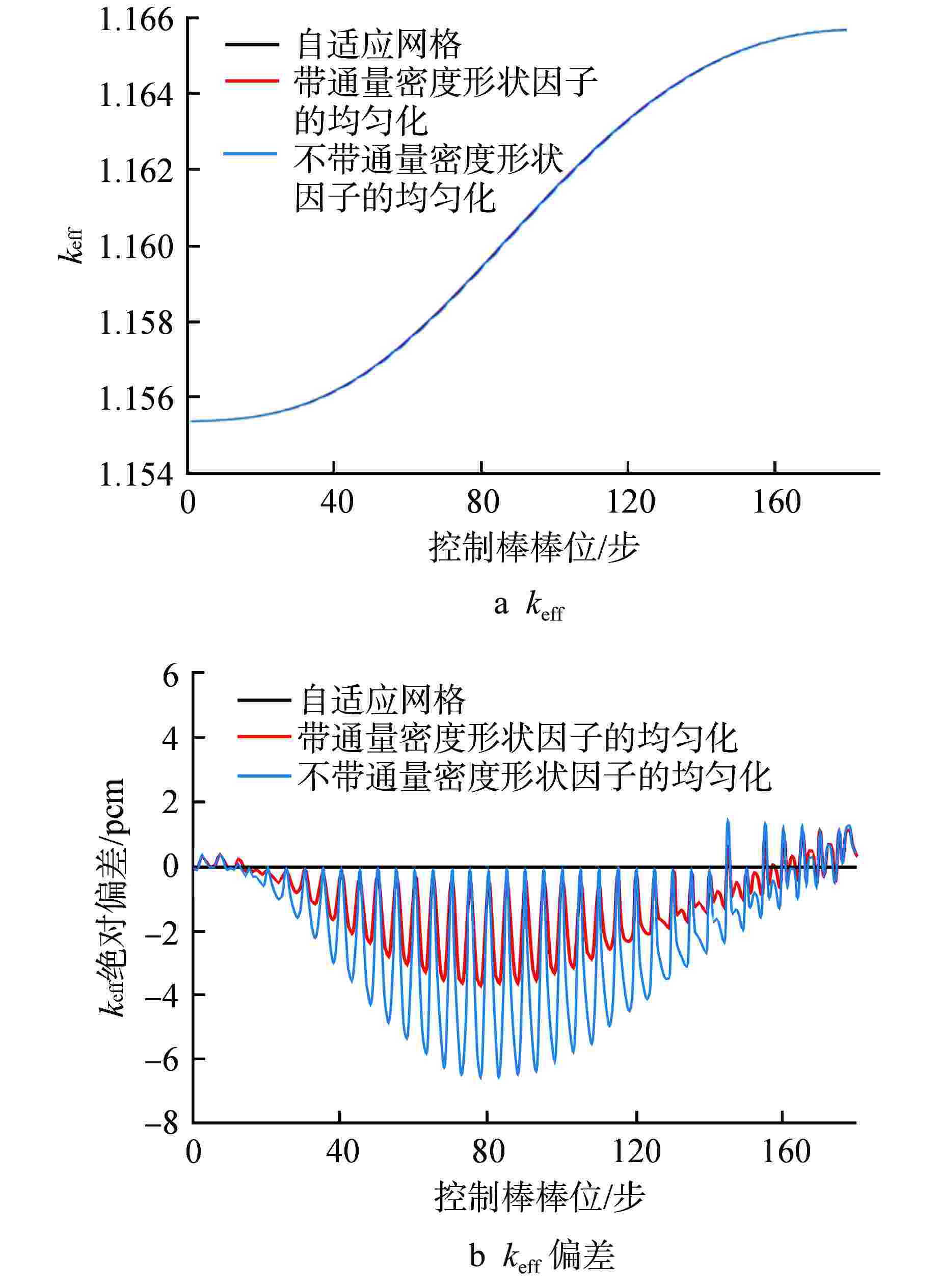
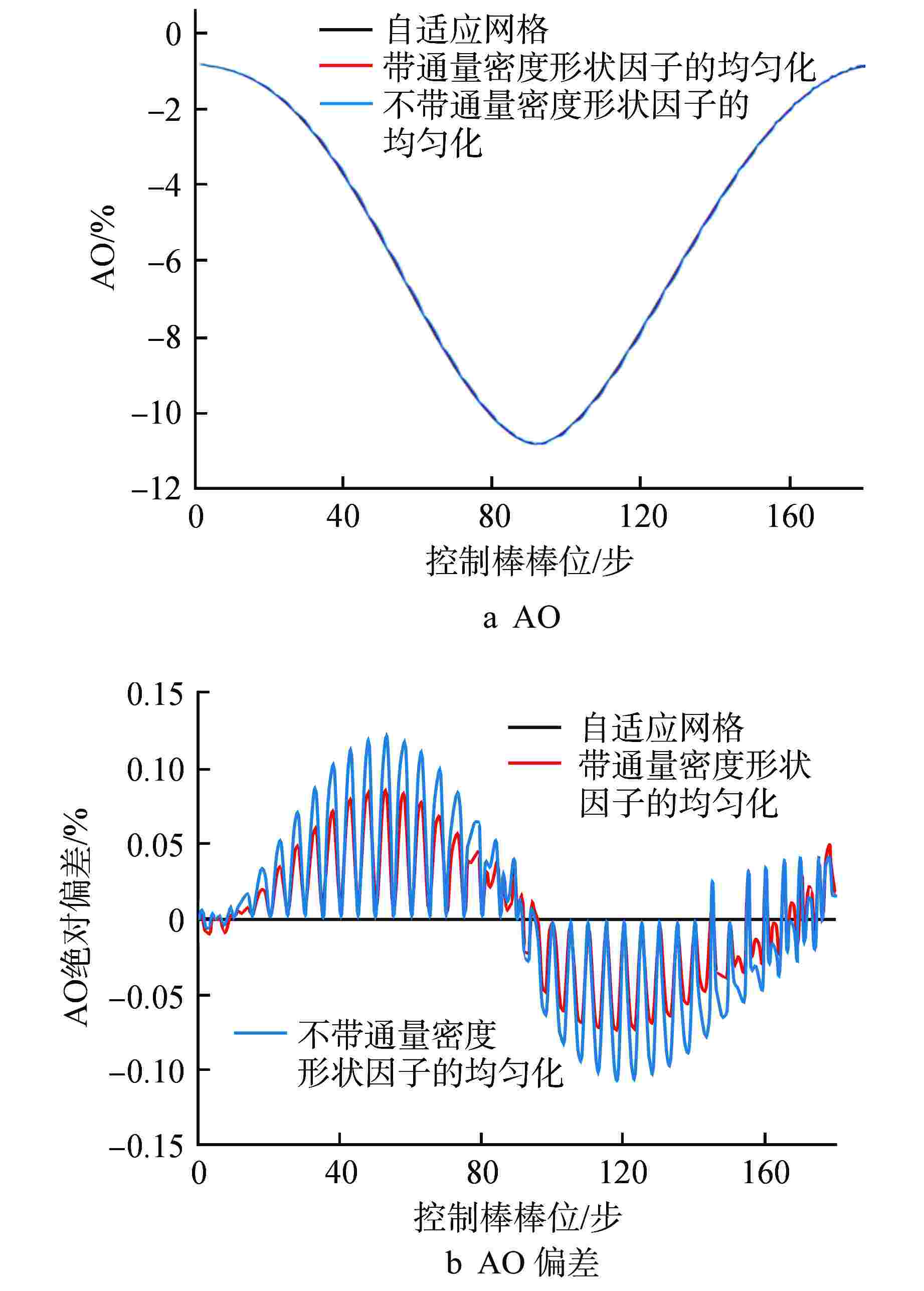
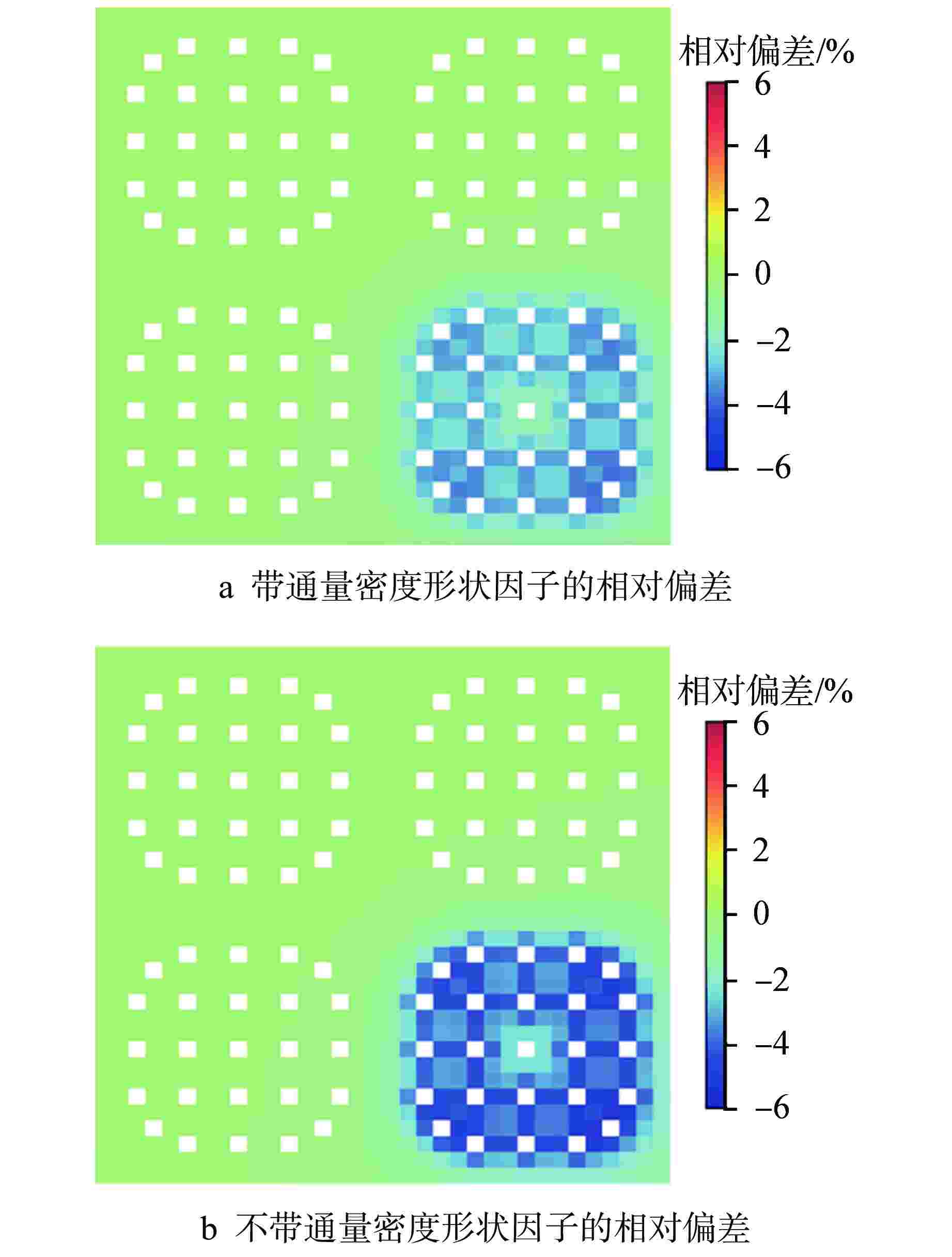
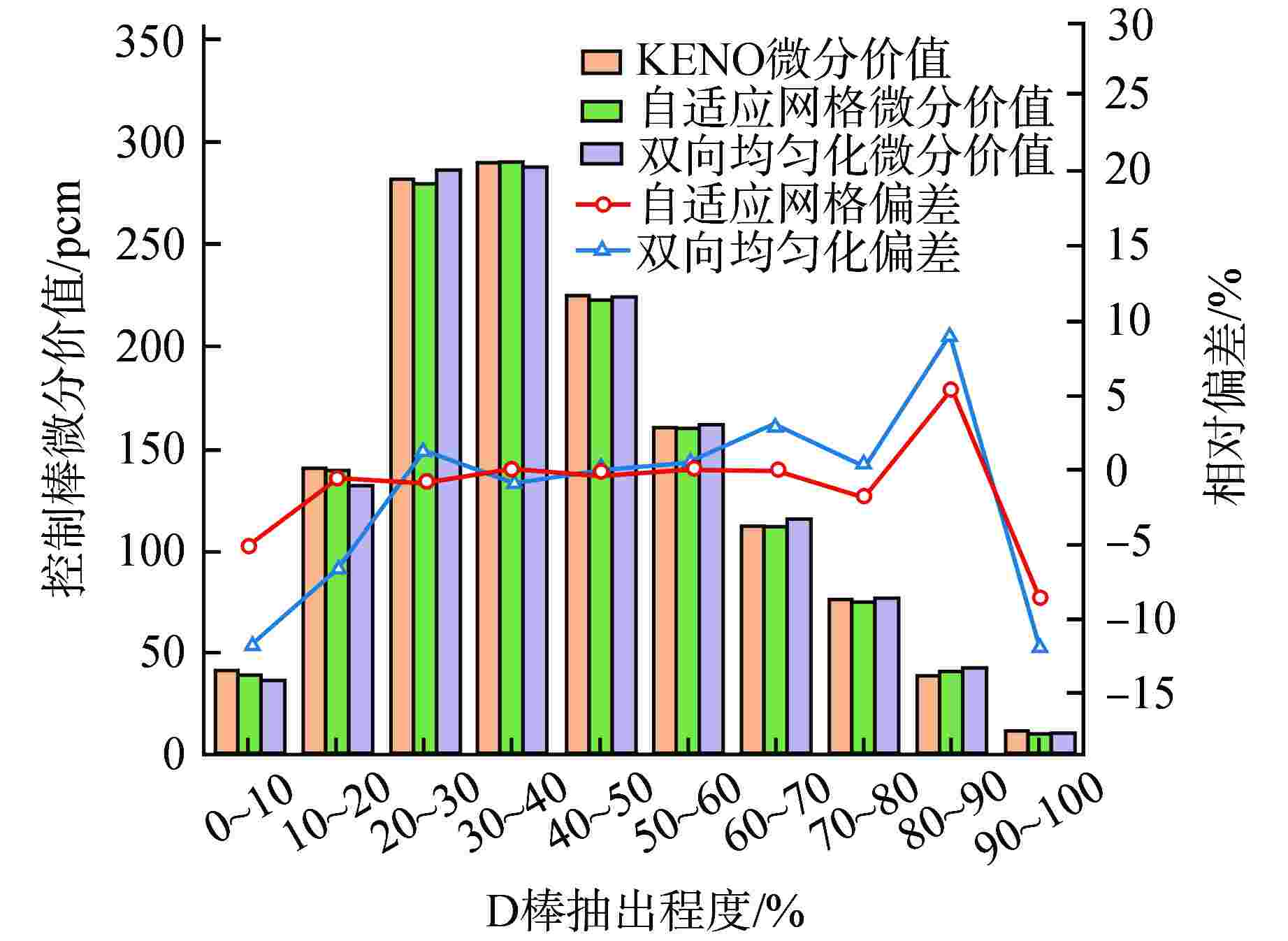
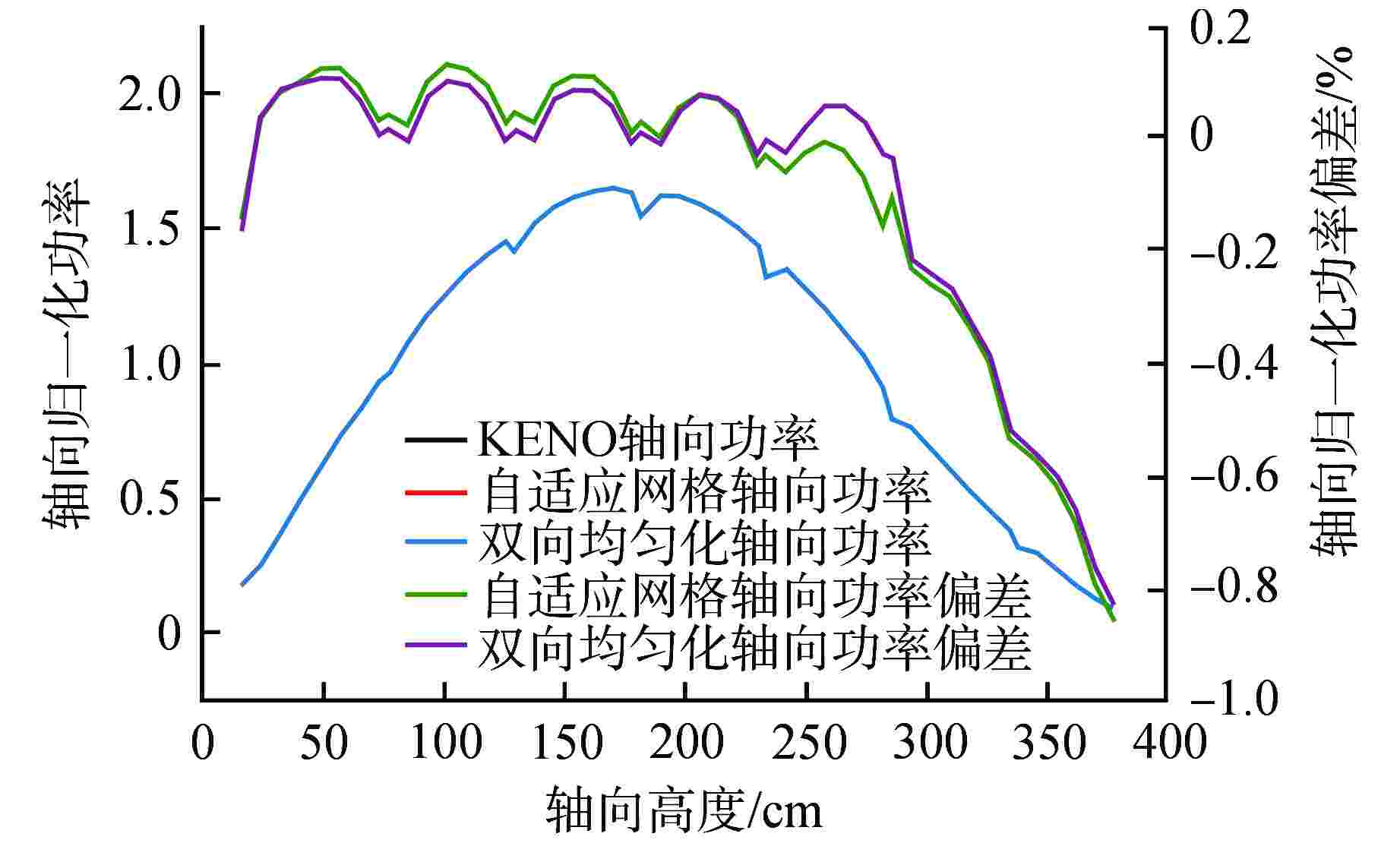
摘要: 在二维/一维耦合特征线输运的基础上，研究了控制棒移动的尖齿效应处理方法，包括自适应网格方法和双向均匀化方法。在双向均匀化方法中，通过建立径向通量密度形状因子和轴向通量密度形状因子降低均匀化的误差。在高保真数值反应堆程序NECP-X中开发了控制棒移动功能，通过C5G7-TD宏观问题和VERA #5全堆芯基准题对控制棒尖齿效应进行验证。数值结果表明：在计算控制棒价值和堆芯功率上自适应网格方法和双向均匀化方法都有较高的计算精度；通量密度形状因子可以很好地修正双向均匀化所带来的尖齿效应。
-
关键词:
- 二维/一维耦合特征线方法 /
- 控制棒尖齿效应 /
- 双向均匀化 /
- 通量密度形状因子 /
- NECP-X
Abstract: On the basis of 2D/1D coupled characteristics transport, the treatment method of cusping effect of control rod movement are studied, including adaptive mesh method and bidirectional homogenization method. In the bidirectional homogenization method, the homogenization error is reduced by establishing radial flux profile and axial flux profile. The control rod movement function is implemented in high fidelity numerical reactor code NECP-X. The treatment of the control rod cusping effect is verified by the C5G7-TD benchmark and VERA #5 benchmark. The numerical results show that the adaptive mesh method and the bidirectional homogenization method both have high accuracy in the calculation of control rod value and core power. The control rod cusping effect caused by bidirectional homogenization can be well corrected by flux profile. -
图 4 部分插入层的一维SN计算示意图
Figure 4. Schematic diagram of 1D SN Calculation of Partially Inserted Layer
图 5 二维/一维耦合输运计算中的双向均匀化示意图
Figure 5. Bidirectional Homogenization in 2D/1D Coupled Transport Calculation
图 6 三维C5G7-TD基准题活性区径向和轴向几何
Figure 6. Radial and Axial Geometry of Active Region of 3D C5G7-TD Benchmark Problem
图 9 部分插入层的径向棒功率分布相对偏差
Figure 9. Relative Error of Pin Power in Partially Inserted Layer
图 11 VERA #5提棒算例的微分价值曲线
Figure 11. Differential Worth of Raising-Rod Cases for VERA #5
表 1 VERA #5提棒算例keff结果
Table 1. keff of Raising-Rod Cases for VERA #5
D棒抽出程度/% KENO-Ⅵ参考解 自适应网格方法 双向均匀化方法 计算值 偏差/pcm 计算值 偏差/pcm 0 0.99276 0.99273 −3 0.99272 −4 10 0.99316 0.99311 −5 0.99308 −8 20 0.99456 0.99450 −6 0.99438 −18 30 0.99737 0.99728 −9 0.99723 −14 40 1.00028 1.00019 −9 1.00011 −17 50 1.00254 1.00244 −10 1.00237 −17 60 1.00416 1.00406 −10 1.00400 −16 70 1.00530 1.00520 −10 1.00517 −13 80 1.00607 1.00595 −12 1.00594 −13 90 1.00647 1.00637 −10 1.00637 −10 100 1.00658 1.00648 −10 1.00647 −11 
下载: 导出CSV
表 2 VERA #5临界算例结果
Table 2. Results of Critical Case for VERA #5
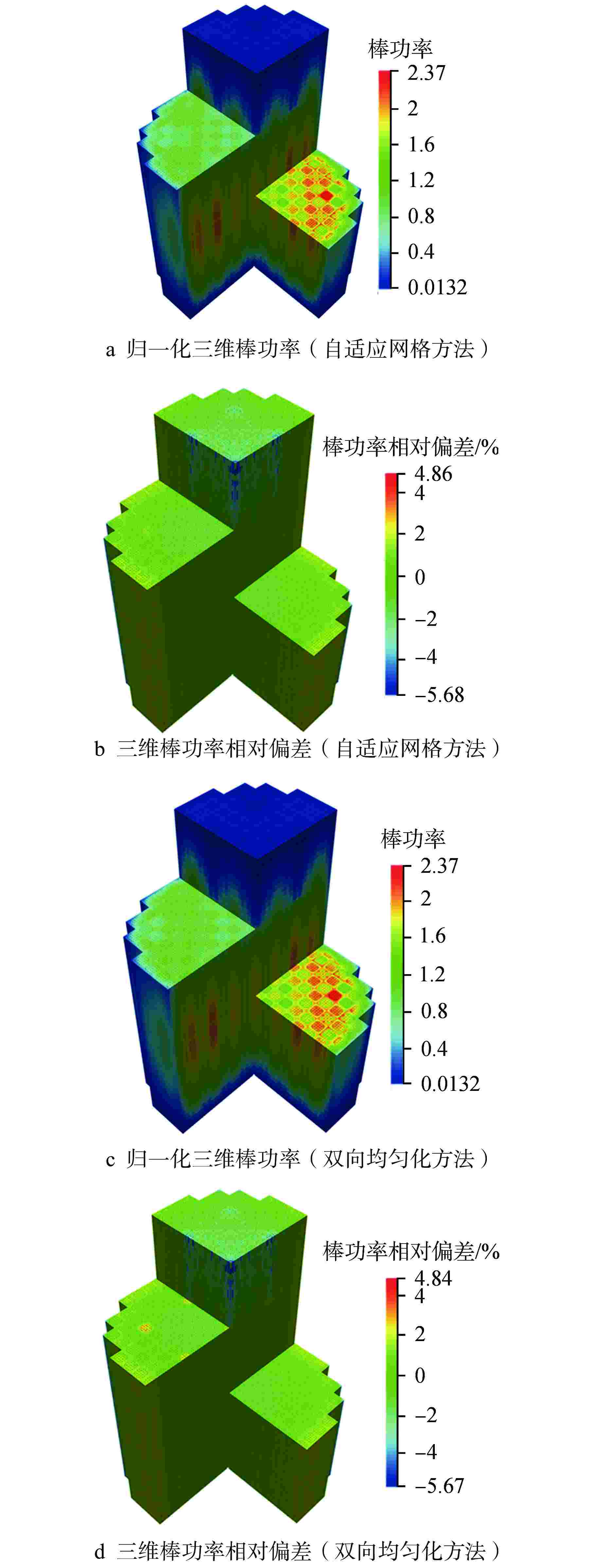
程序/方法 keff keff偏差/pcm 最大棒功率
偏差/%棒功率偏差
均方根/%KENO-Ⅵ 0.99990 自适应网格方法 0.99978 −12 −5.67 0.77 双向均匀化方法 0.99979 −11 −5.67 0.77
下载: 导出CSV
-
[1] YAMAMOTO A. A simple and efficient control rod cusping model for three-dimensional pin-by-pin core calculations[J]. Nuclear Technology, 2004, 145(1): 11-17. doi: 10.13182/NT145-11 [2] CHO B, CHO N Z. A nonoverlapping local/global iterative method with 2-D/1-D fusion transport kernel and p-CMFD wrapper for transient reactor analysis[J]. Annals of Nuclear Energy, 2015, 85: 937-957. doi: 10.1016/j.anucene.2015.07.012 [3] GRAHAM, AARON M, COLLINS, et al. Subplane-based control rod decusping techniques for the 2D/1D method in MPACT[C]//International Conference on Mathematics & Computational Methods Applied to Nuclear Science& Engineering, Jeju: USB, 2017. [4] CHO H H, KANG J, YOON J I, et al. Analysis of C5G7-TD benchmark with a multi-group pin homogenized SP3 code SPHINCS[J]. Nuclear Engineering and Technology, 2021, 53(5): 1403-1415. doi: 10.1016/j.net.2020.11.013 [5] 王博. 核反应堆高保真物理热工耦合瞬态分析方法研究及其应用[D]. 西安: 西安交通大学, 2021. [6] HOU J, IVANOV K N, BOYARINOV V F, et al. OECD/NEA benchmark for time-dependent neutron transport calculations without spatial homogenization[J]. Nuclear Engineering and Design, 2017, 317: 177-189. doi: 10.1016/j.nucengdes.2017.02.008 [7] CHEN J, LIU Z Y, ZHAO C, et al. A new high-fidelity neutronics code NECP-X[J]. Annals of Nuclear Energy, 2018, 116: 417-428. doi: 10.1016/j.anucene.2018.02.049 [8] ORNL. VERA Core Physics Benchmark Progression Problem Specifications: CASL-U-2012-0131-004 [R]. Tennessee: Oak Ridge National Laboratory, 2014. -
计量
- 文章访问数: 100
- HTML全文浏览量: 30
- PDF下载量: 16
- 被引次数: 0
