Study on Circumferential Non-Uniformity of Annular Fuel Outer Temperature Distribution in Lead-bismuth Cooled Tight Cell
-
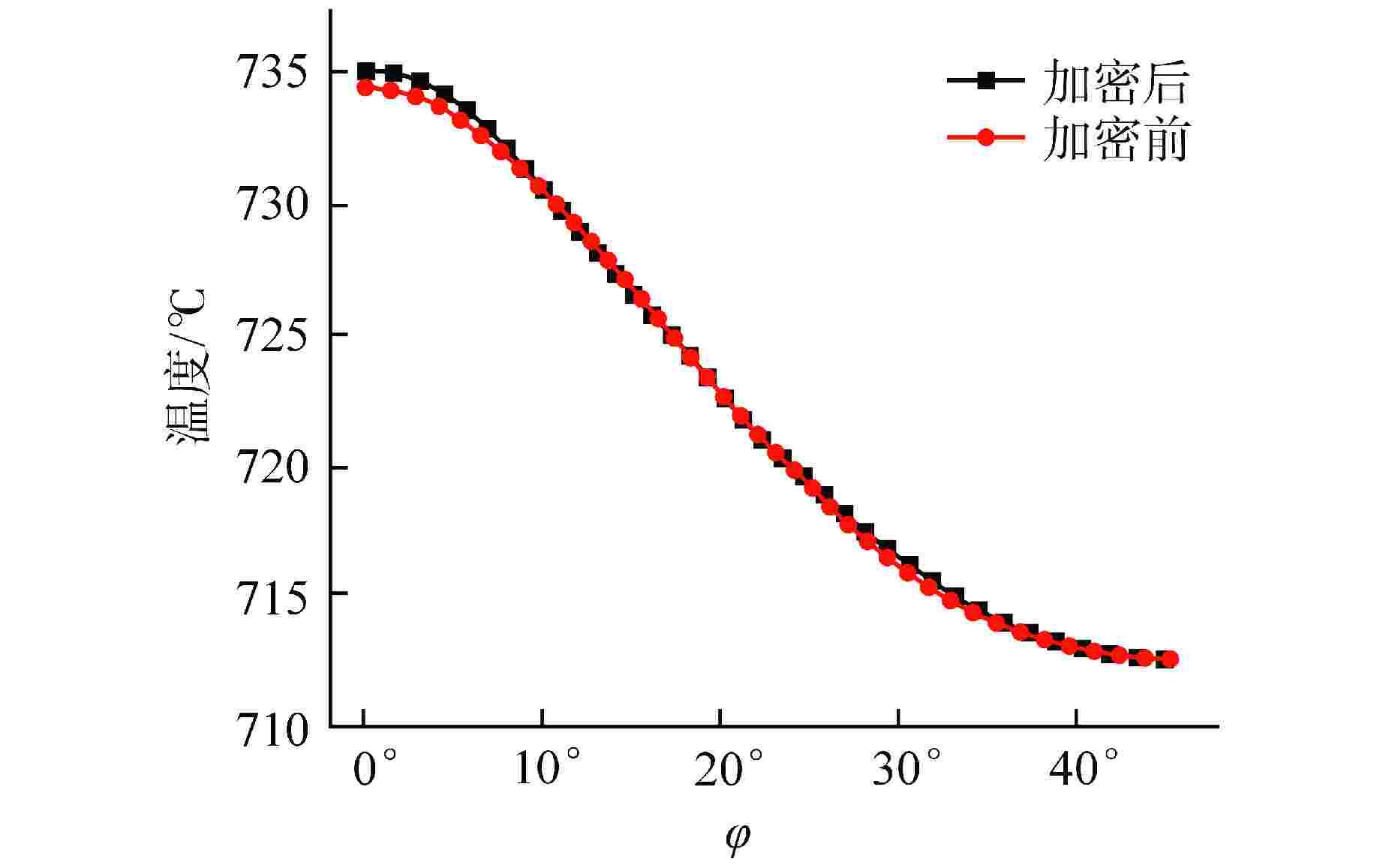
摘要: 对于采用紧密排布结构的反应堆，分析燃料棒外包壳周向温度分布不均匀性对防止包壳热应力失效尤为重要。本文采取理论分析模型和数值拟合模型结合的方式，得出了在稳态工况下铅铋冷却紧密栅内环形燃料棒外周向温度分布的数值拟合式，并与计算流体动力学（CFD）数值模拟数据进行了对比。结果表明，本文得出的数值拟合式具有良好的准确性，可为采用环形燃料元件的铅铋反应堆的燃料包壳周向温度分析研究提供理论依据。
-
关键词:
- 环形燃料 /
- 周向温度分布 /
- 数值拟合 /
- 铅铋反应堆 /
- 计算流体动力学（CFD）
Abstract: For the reactor with closely arranged structure, it is particularly important to analyze the non-uniformity of circumferential temperature distribution of fuel rod cladding to prevent thermal stress failure of the cladding. In this paper, the theoretical analysis model is combined with the numerical fitting model, and the numerical fitting formula of the circumferential temperature distribution of the annular fuel rod in the lead-bismuth cooled tight cell is obtained under steady-state conditions, and compared with the numerical simulation data of computational fluid dynamics (CFD). The results show that the numerical fitting formula obtained in this paper has good accuracy, which can provide theoretical basis for the circumferential temperature analysis of fuel cladding of lead-bismuth reactor with annular fuel elements. -
图 6 坐标变换后的无量纲温度分布
Figure 6. Dimensionless Temperature Distribution after Coordinate Transformation
图 7 拟合式结果与数值计算结果的对比
Figure 7. Comparison of Fitting Results and Numerical Calculation Results
表 1 环形燃料初始几何尺寸设计参数
Table 1. Design Parameters of Initial Geometric Dimensions of Annular Fuel
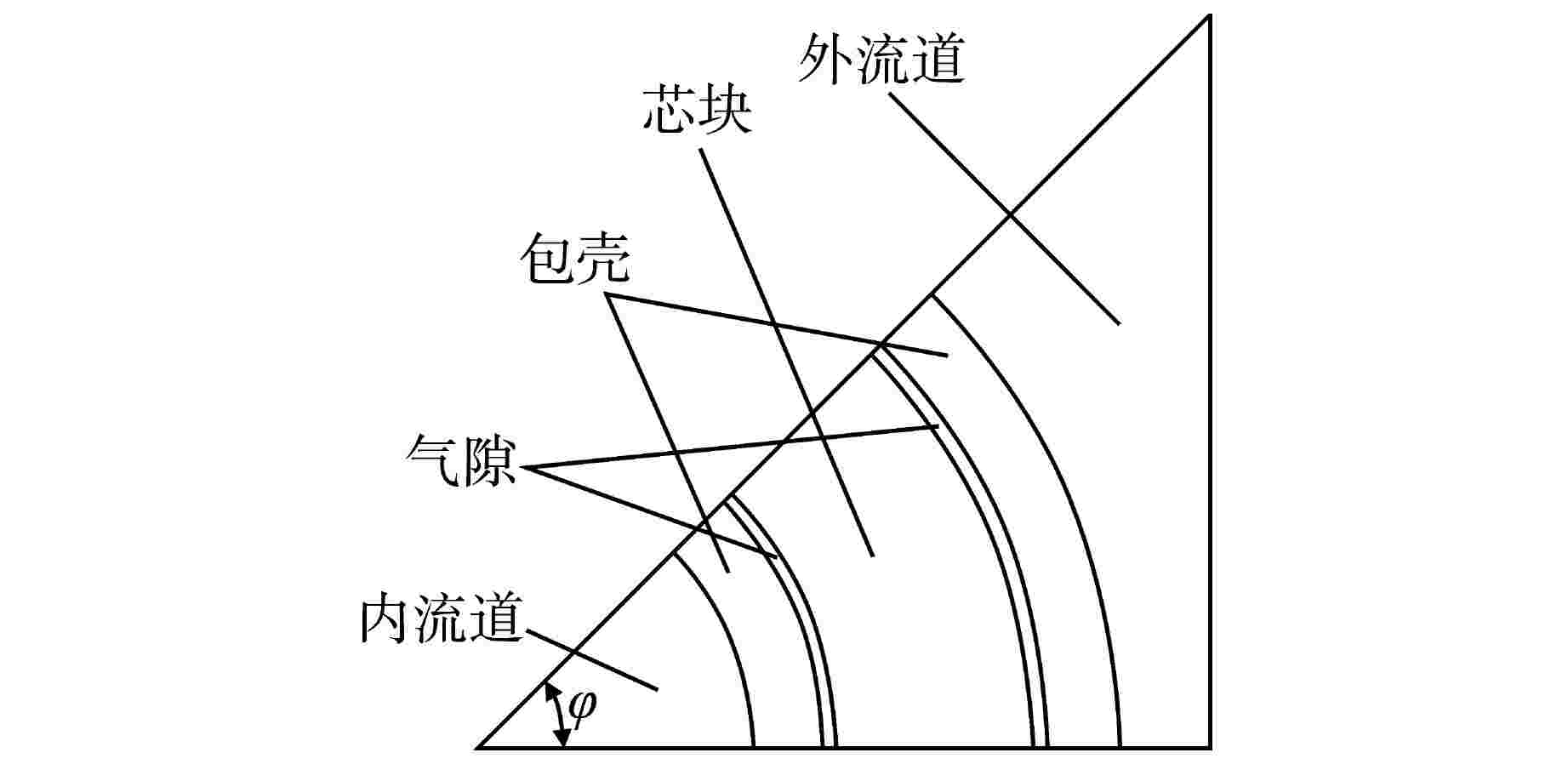
参数名 参数值/mm 内包壳内径 8.33 内包壳外径 9.48 燃料芯块内径 9.60 燃料芯块外径 13.75 外包壳内径 13.88 外包壳外径 15.52 有效加热长度 1000 
下载: 导出CSV
表 2 材料物性参数
Table 2. Physical Properties of the Material
物性参数 间隙 芯块 包壳 氦气 烧结UO2 T91钢 密度/(kg·m−3) 2.425 10994 7700 导热系数/(W·m−1·K−1) 0.51 3.9192 26 比热容/(J·kg−1·K−1) 5191 307 622 粘度/(Pa·s） 3.78×10−5
下载: 导出CSV
表 3 拟合结果的各项参数
Table 3. Parameters of Fitting Results
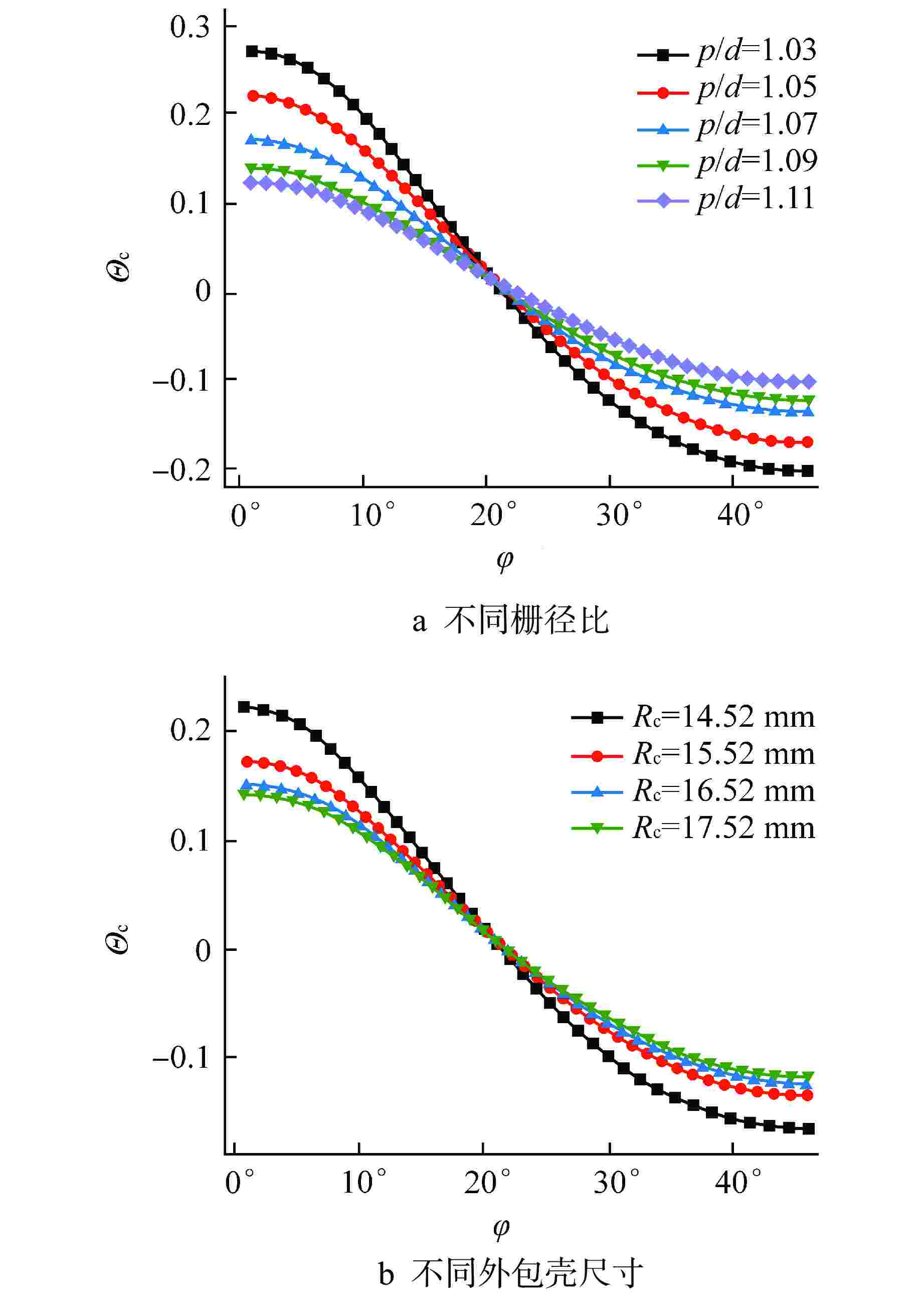
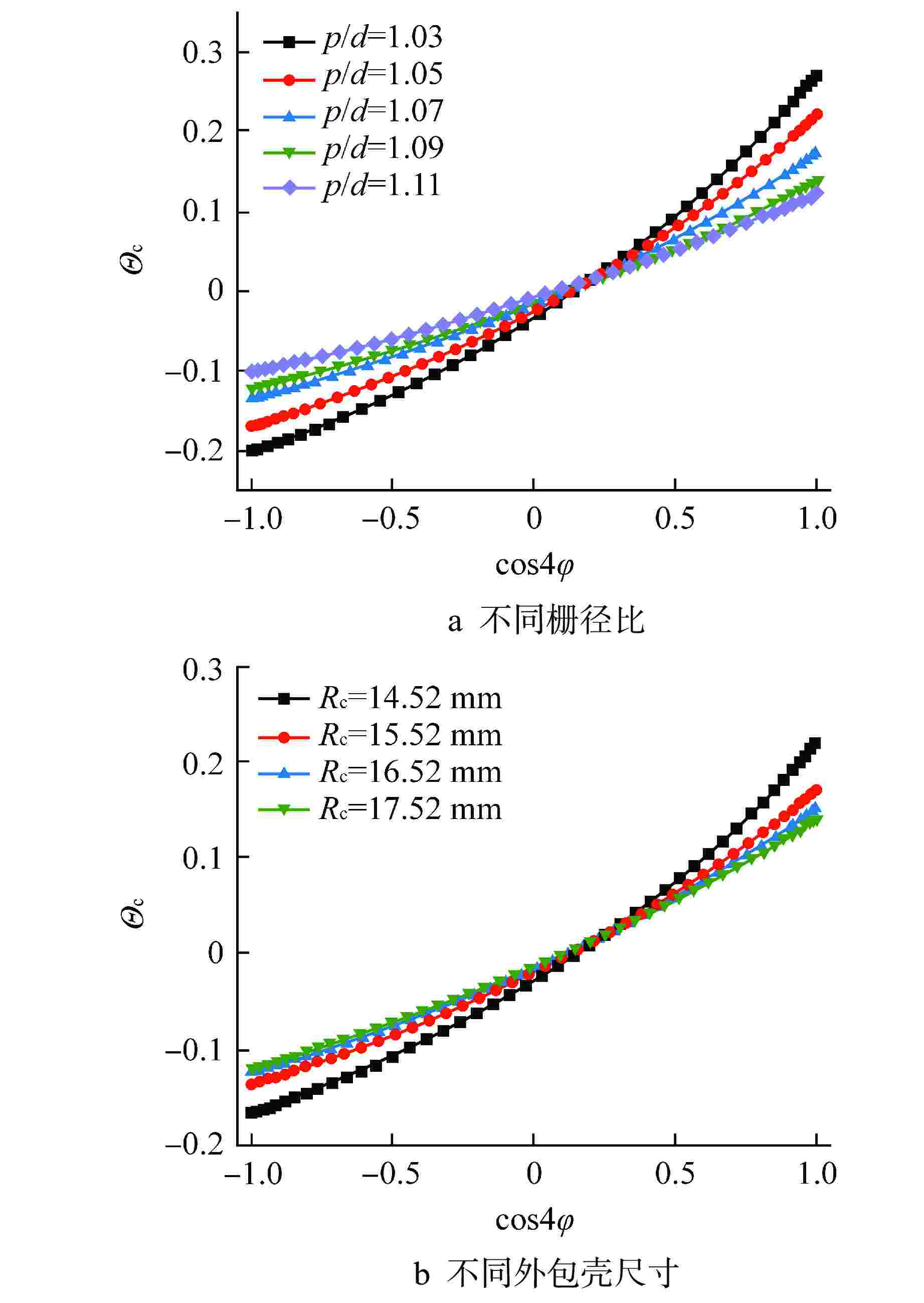
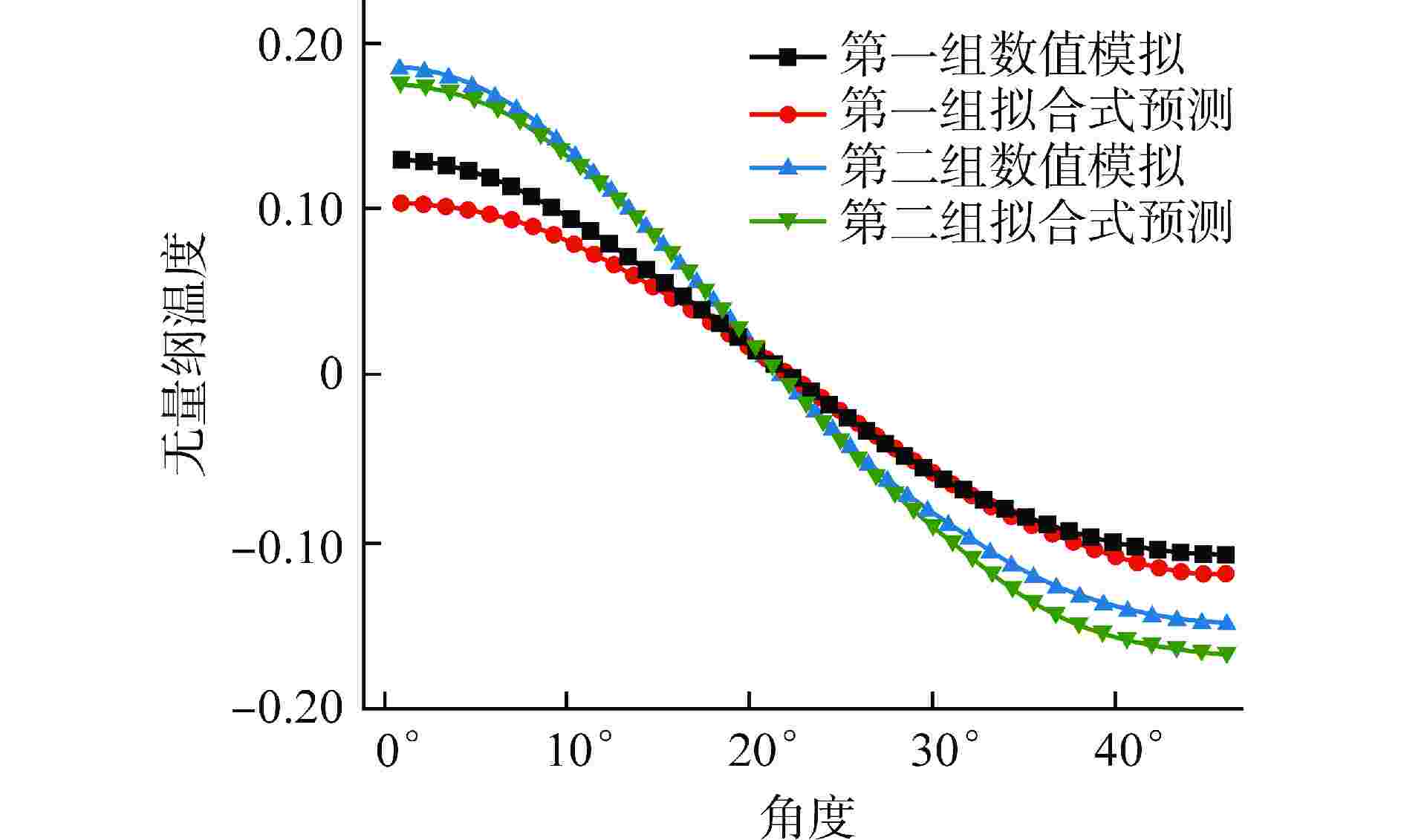
组别 常数项系数C 一次项系数B 二次项系数A 拟合度R2 p/d=1.03 −0.03659 0.23404 0.07151 0.99979 p/d=1.05 −0.02619 0.19275 0.05096 0.99975 p/d=1.07 −0.01846 0.15193 0.03685 0.99983 p/d=1.09 −0.01848 0.12960 0.02638 0.99988 p/d=1.11 −0.00960 0.11142 0.02010 0.99992 Rc=14.52 mm −0.02901 0.18997 0.05643 0.99956 Rc=16.52 mm −0.01546 0.13663 0.02948 0.99983 Rc=17.52 mm −0.01312 0.12912 0.02471 0.99986
下载: 导出CSV
表 4 栅径比对系数拟合效果
Table 4. Fitting Results of Cell-diameter Ratio and Coefficient
系数 拟合表达式 拟合度R2 C $ 0.30845p/d-0.351905 $ 0.90726 B $669065.03919\mathrm{e}\mathrm{x}\mathrm{p}(-14.6864\cdot p/d)+0.05503$ 0.99513 A $ 0.11908{(p/d)}^{-17.32026} $ 0.99959
下载: 导出CSV
表 5 燃料芯块半径和包壳半径比对系数拟合效果
Table 5. Fitting Results of Fuel Pellet Radius-Cladding Radius Ratio and Coefficient
系数 拟合表达式 拟合度R2 C $ 0.00993-1.06709\times {10}^{-8}\mathrm{e}\mathrm{x}\mathrm{p}(15.08359\cdot {R}_{\mathrm{f}}/{R}_{\mathrm{c}}) $ 0.99172 B $ -0.03427+2.96977\times {10}^{-7}\mathrm{e}\mathrm{x}\mathrm{p}(13.0482\cdot {R}_{\mathrm{f}}/{R}_{\mathrm{c}}) $ 0.99988 A $ -0.01675-2.95668\times {10}^{-7}\mathrm{e}\mathrm{x}\mathrm{p}(12.3725\cdot {R}_{\mathrm{f}}/{R}_{\mathrm{c}}) $ 0.99733
下载: 导出CSV
表 6 数值拟合表达式内的各常数值
Table 6. Constant Values in the Numerical Fitting Expression
序号i 二次项常数Ai 一次项常数Bi 常数项常数Ci 1 0.119 669065.039 0.308 2 −17.320 −14.686 −1.07×10−8 3 −2.95668×10−7 2.97×10−7 15.084 4 12.373 13.048 −0.342 5 0.017 0.021
下载: 导出CSV
-
[1] 季松涛,何晓军,张爱民,等. 压水堆核电站采用环形燃料元件可行性研究[J]. 原子能科学技术,2012, 46(10): 1232-1236. [2] MORRA P. Design of annular fuel for high power density BWRs[D]. Cambridge: Massachusetts Institute of Technology, 2004. [3] OLDEKOP W, BERGER H D, ZEGGEL W. General features of advanced pressurized water reactors with improved fuel utilization[J]. Nuclear Technology, 1982, 59(2): 212-227. doi: 10.13182/NT82-A33024 [4] OKA Y, KOSHIZUKA S. Design concept of once-through cycle supercritical-pressure light water cooled reactors[C]//Proceedings of the First International Symposium on Supercritical Water-Cooled Reactors, Design and Technology. Tokyo: The University of Tokyo, 2000: 1-22. [5] GU H Y, CHENG X, YANG Y H. CFD analysis of thermal–hydraulic behavior in SCWR typical flow channels[J]. Nuclear Engineering and Design, 2008, 238(12): 3348-3359. doi: 10.1016/j.nucengdes.2008.06.010 [6] 魏君翰, 赵民富. 环形燃料棒束冷却剂流动的数值模拟研究[C]//第十六届全国反应堆热工流体学术会议暨中核核反应堆热工水力技术重点实验室2019年学术年会论文集. 北京: 中国核学会核能动力分会反应堆热工流体专业委员会, 2019: 1311-1321. [7] GOU J L, SHANG Z, ISHIWARARI Y, et al. CFD analysis of heat transfer in subchannels of a super fast reactor[J]. Nuclear Engineering and Design, 2010, 240(7): 1819-1829. doi: 10.1016/j.nucengdes.2010.03.013 [8] CASTRO L, FRANÇOIS J L, GARCÍA C. Coupled Monte Carlo-CFD analysis of heat transfer phenomena in a supercritical water reactor fuel assembly[J]. Annals of Nuclear Energy, 2020, 141: 107312. doi: 10.1016/j.anucene.2020.107312 [9] 何斯琪,赵冬建,于意奇,等. 7棒束紧密栅元流体流动传热数值研究[J]. 原子能科学技术,2012, 46(S1): 199-205. [10] CHEN Z, ZHOU G M, ZHOU T, et al. CFD analysis of circumferential temperature distribution on fuel cladding surface of China lead alloy cooled research reactor (CLEAR-I)[C]//2013 21st International Conference on Nuclear Engineering. Chengdu: American Society of Mechanical Engineers, 2013: V003T10A031. [11] ZHANG Y N, ZHANG C, JIANG J. Numerical simulation of fluid flow and heat transfer of supercritical fluids in fuel bundles[J]. Journal of Nuclear Science and Technology, 2011, 48(6): 929-935. doi: 10.1080/18811248.2011.9711779 [12] 陶文铨. 数值传热学[M]. 第二版, 西安: 西安交通大学出版社, 2001: 424-427. [13] 孔珑. 工程流体力学[M]. 第二版, 北京: 中国电力出版社, 1992: 103-109. [14] 邓阳斌,巫英伟,张伟旭,等. 双面冷却环形燃料元件的几何尺寸优化[J]. 原子能科学技术,2015, 49(7): 1208-1214. [15] 李华琪, 陈森, 杨宁, 等. 双面冷却环形燃料元件热工水力特性分析[C]//中国核科学技术进展报告（第六卷）——中国核学会2019年学术年会论文集第3册（核能动力分卷）. 北京: 中国核学会, 2019: 51-59. [16] 基里洛夫. 核工程用材料的热物理性质[M]. 吴兴曼, 郑颖, 张玲, 译. 北京: 原子能出版社, 2011: 93-102. -
计量
- 文章访问数: 90
- HTML全文浏览量: 23
- PDF下载量: 27
- 被引次数: 0
