Study on Low-cycle Fatigue Test Method for Zr-Sn-Nb Alloy Welded Sheets
-
摘要: 为研究锆合金焊接薄板的低周疲劳（LCF）性能，基于锆合金薄板的LCF试验方法，结合组织模拟和有限元方法，从显微组织、显微硬度和单轴拉伸性能等方面对比评估，证实采用组织模拟方法简化焊接接头漏斗试样复杂组织结构基本可行，最终基于耦合建立了焊接薄板漏斗试样的应力应变转换，并采用该方法对焊接薄板LCF性能进行评价。研究结果表明，本研究建立的锆合金焊接薄板的LCF试验方法能够用于评价焊接薄板的LCF性能。Abstract: In order to study the low cycle fatigue (LCF) properties of Zr-Sn-Nb alloy welded sheets, microstructure simulation and finite element method were combined based on the LCF test method of Zr-Sn-Nb alloy sheets in this study. The microstructure, microhardness and uniaxial tensile properties were compared and evaluated, and it turned out that it was basically feasible to simplify the complex microstructure of welded joint funnel sample by microstructure simulation. Finally, the stress-strain transformation of welded sheet funnel sample was established based on coupling, and the LCF properties of welded sheets were evaluated by this method. The results show that the LCF test method established in this study for Zr-Sn-Nb alloy welded sheets can be used to evaluate the LCF properties of the welded sheets.
-
Key words:
- Zr-Sn-Nb Alloy /
- Welded Sheets /
- Welded Joint /
- Finite element /
- Low cycle fatigue (LCF)
-
图 2 淬火再退火后的显微组织
Figure 2. Microstructure of Quenched and Then Annealed Uniaxial Tensile Sample
图 4 再结晶态、淬火及淬火再退火态单轴拉伸曲线
Figure 4. Uniaxial Tensile Curves of Recrystallized, Quenched and Quenched and Then Annealed Sample
图 5 淬火再退火拉伸断口形貌
Figure 5. Fractography of Quenched and Then Annealed Uniaxial Tensile Sample
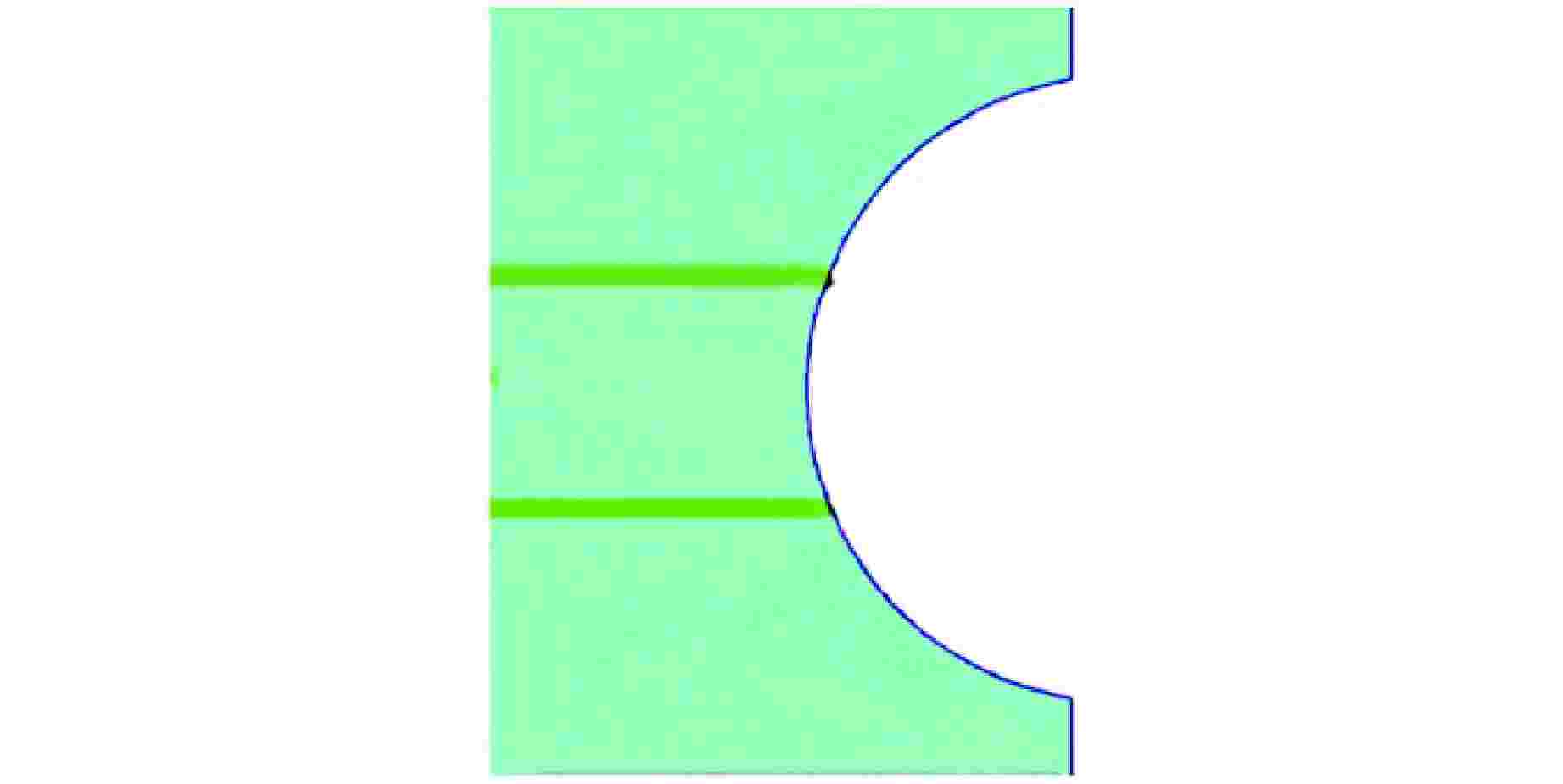
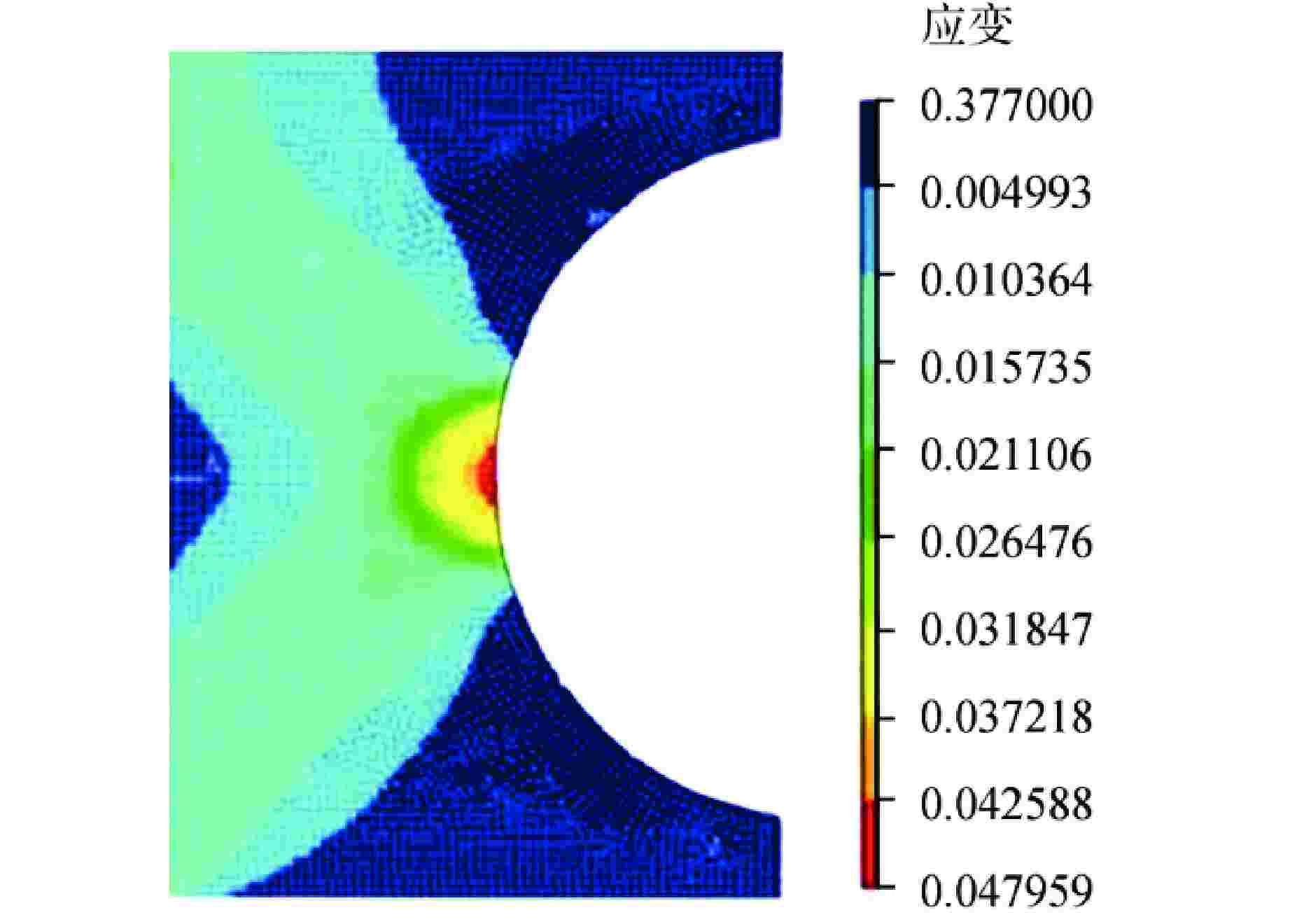
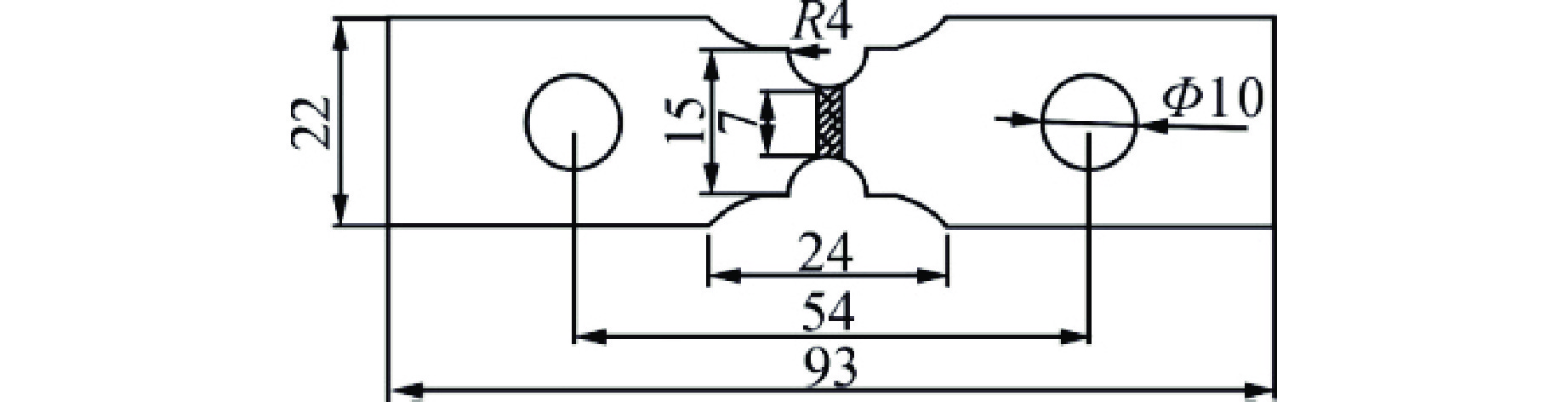
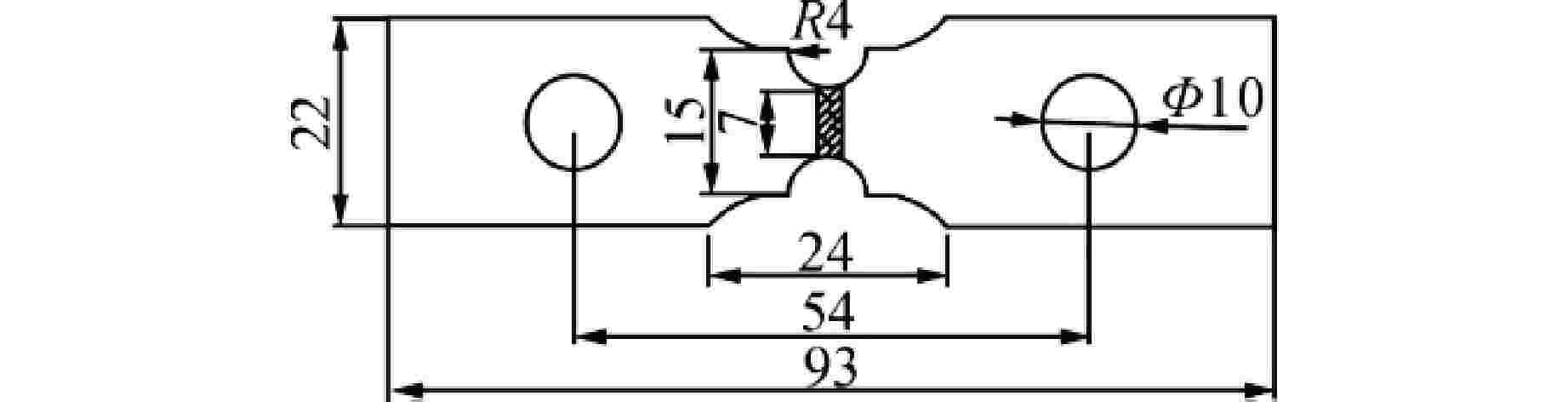
图 9 焊接薄板漏斗试样
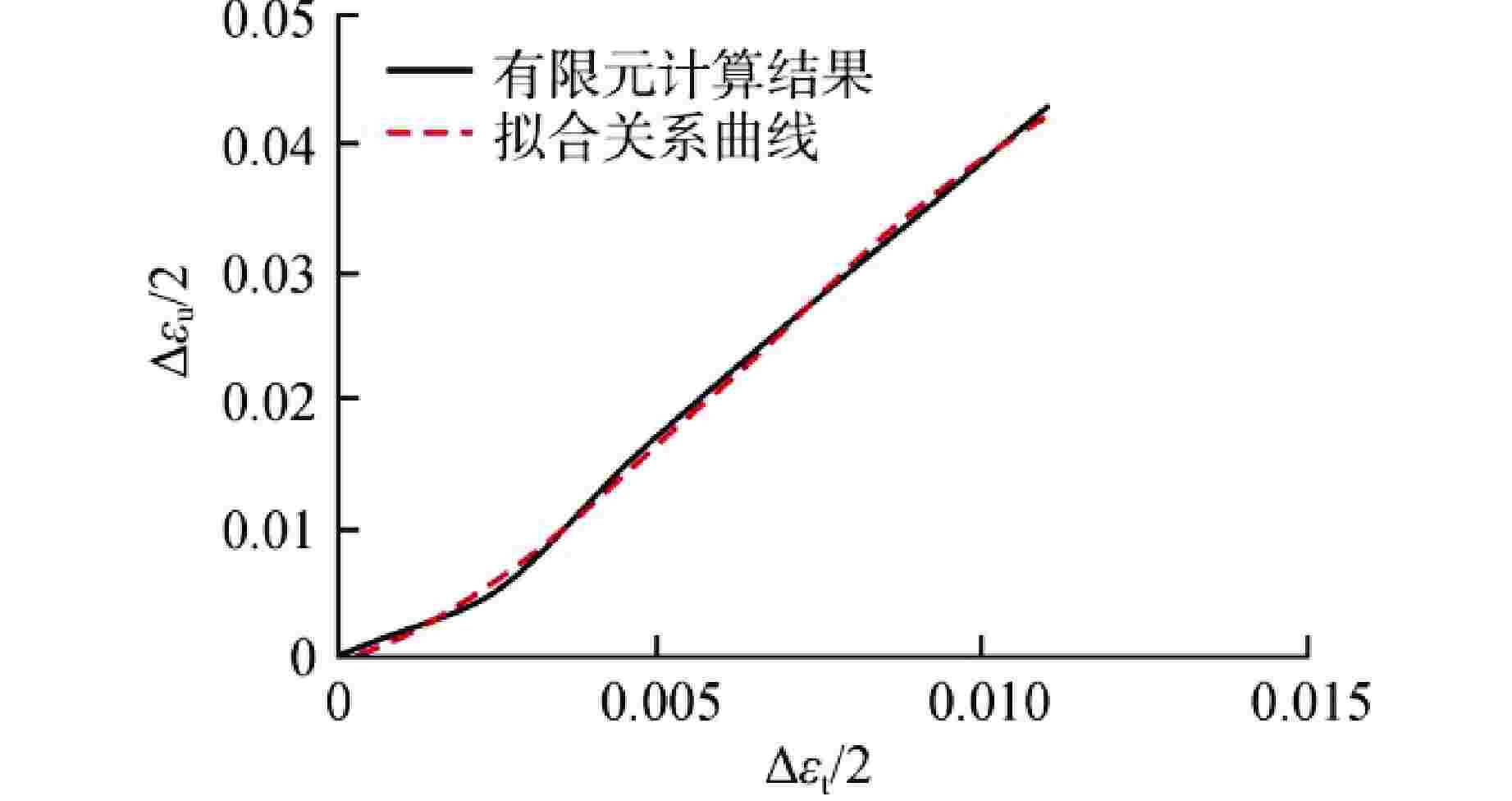
$ \left( {{{{{\Delta }}{\varepsilon _{\text{u}}}} \mathord{\left/ {\vphantom {{{{\Delta }}{\varepsilon _{\text{u}}}} 2}} \right. } 2}} \right) $ 与$ \left( {{{{{\Delta }}{\varepsilon _{\text{t}}}} \mathord{\left/ {\vphantom {{{{\Delta }}{\varepsilon _{\text{t}}}} 2}} \right. } 2}} \right) $ 关系Figure 9. Relationship between
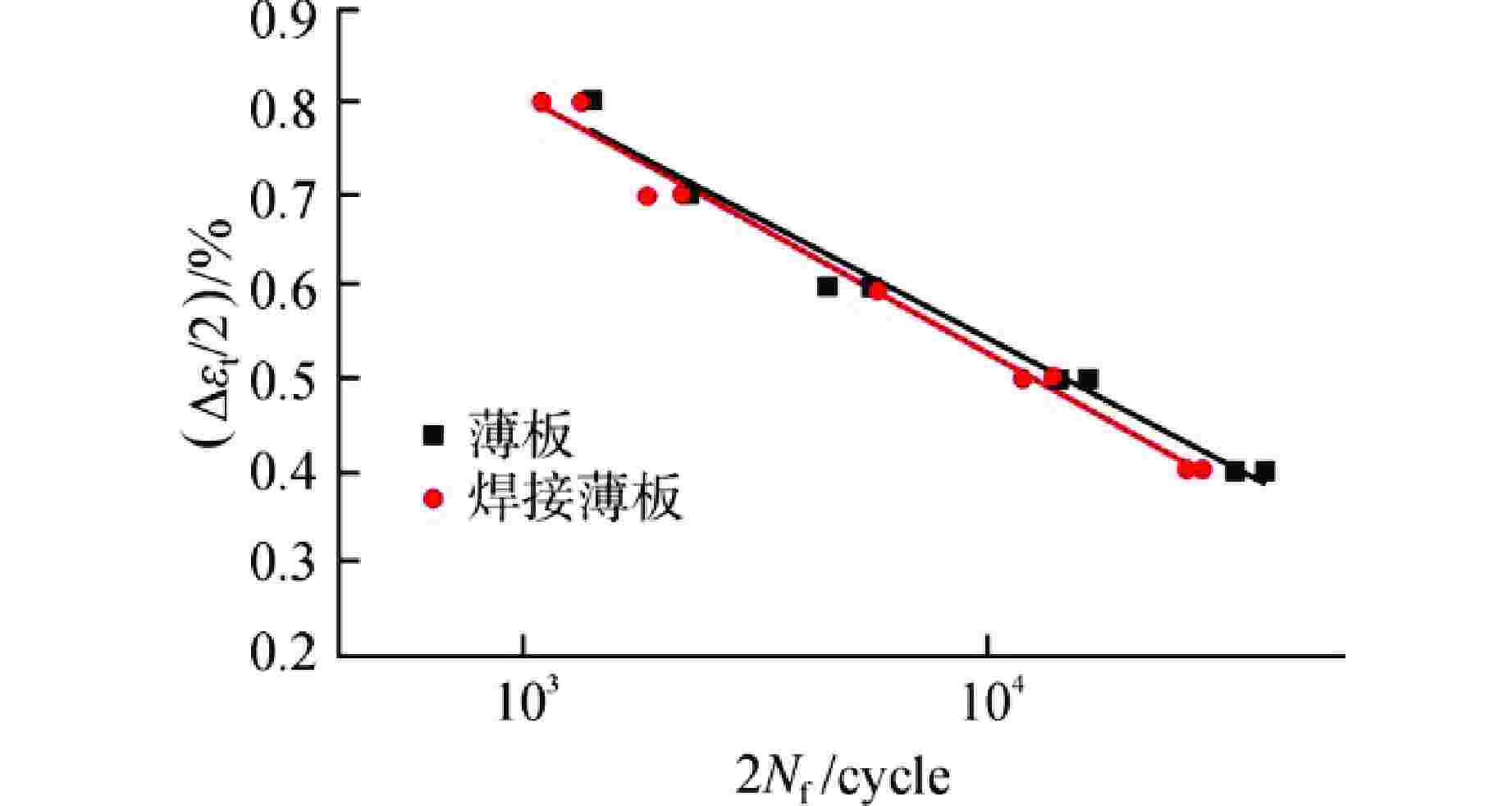
$ \left( {{{{{\Delta }}{\varepsilon _{\text{u}}}} \mathord{\left/ {\vphantom {{{{\Delta }}{\varepsilon _{\text{u}}}} 2}} \right. } 2}} \right) $ and$ \left( {{{{{\Delta }}{\varepsilon _{\text{t}}}} \mathord{\left/ {\vphantom {{{{\Delta }}{\varepsilon _{\text{t}}}} 2}} \right. } 2}} \right) $ of Welded Sheet Funnel Sample
图 10 转换前薄板和焊接薄板的
$ \left( {{{{{\Delta }}{\varepsilon _{\text{t}}}} \mathord{\left/ {\vphantom {{{{\Delta }}{\varepsilon _{\text{t}}}} 2}} \right. } 2}} \right) $ -2Nf曲线[7]Figure 10.
$ \left( {{{{{\Delta }}{\varepsilon _{\text{t}}}} \mathord{\left/ {\vphantom {{{{\Delta }}{\varepsilon _{\text{t}}}} 2}} \right. } 2}} \right) $ -2Nf Curves of Sheets and Welded Sheets before Conversion[7]
图 11 转换后薄板和焊接薄板的
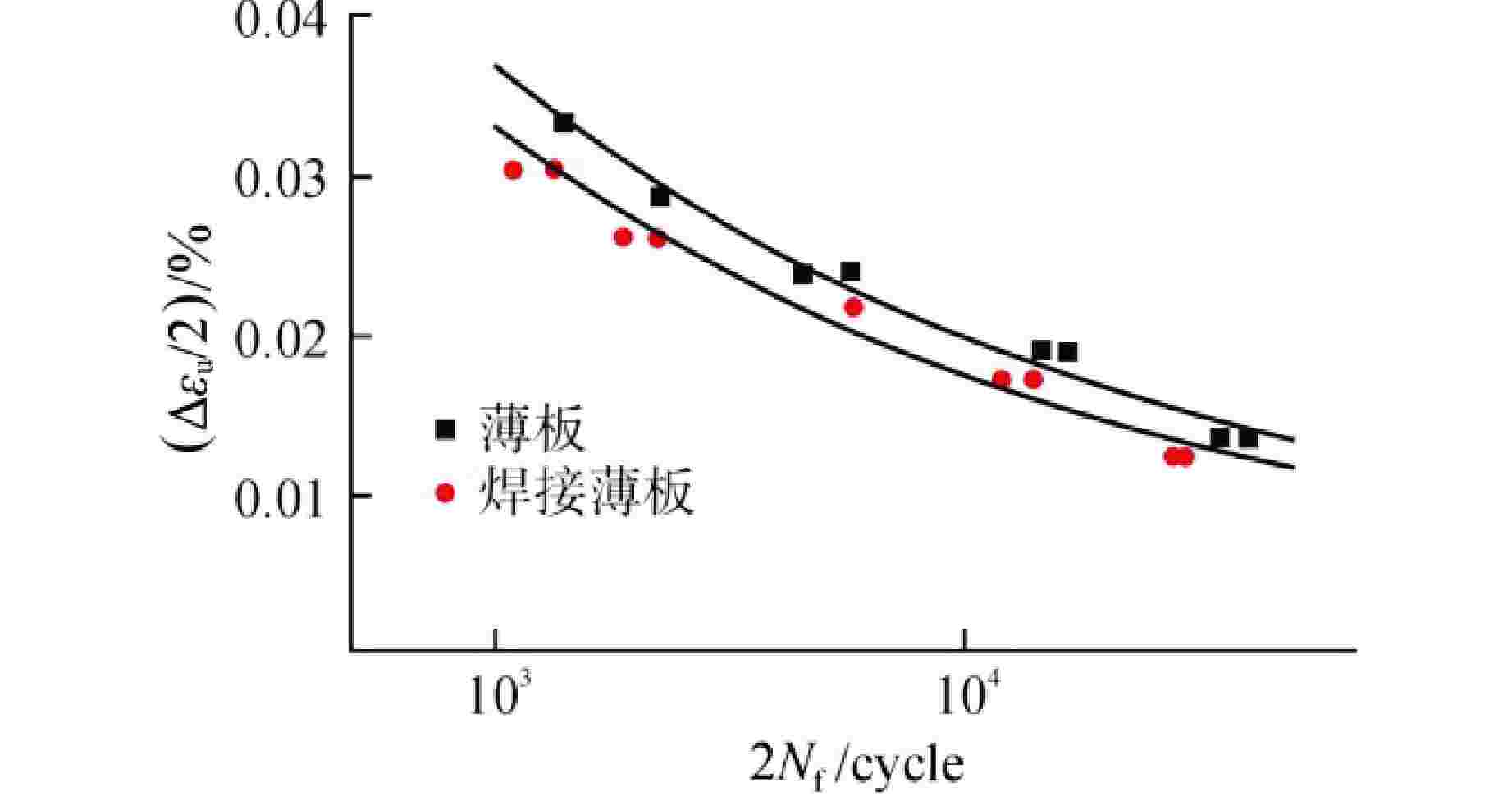
$ \left( {{{{{\Delta }}{\varepsilon _{\text{u}}}} \mathord{\left/ {\vphantom {{{{\Delta }}{\varepsilon _{\text{u}}}} 2}} \right. } 2}} \right) $ -2Nf曲线及Manson-Coffin关系Figure 11.
$ \left( {{{{{\Delta }}{\varepsilon _{\text{u}}}} \mathord{\left/ {\vphantom {{{{\Delta }}{\varepsilon _{\text{u}}}} 2}} \right. } 2}} \right) $ -2Nf Curves of Sheets and Welded Sheets after Conversion amd Manson-Coffin Relationship表 1 试验材料化学成分
Table 1. Chemical Composition of Test Material
元素 Sn Nb Fe Cr Zr 质量分数/% 0.96 0.32 0.36 0.078 余量 
下载: 导出CSV
表 3 薄板及焊接薄板的维氏硬度值
Table 3. Vickers Hardness of Sheets and Welded Sheets
材料状态 模拟组织 焊缝 热影响区 母材区 维氏硬度 162 189 171 160
下载: 导出CSV
表 5 各级
$ \left( {{{{{\Delta }}{\varepsilon _{\text{t}}}} \mathord{\left/ {\vphantom {{{{\Delta }}{\varepsilon _{\text{t}}}} 2}} \right. } 2}} \right) $ 对应的漏斗试样$ \left( {{{{{\Delta }}{\varepsilon _{\text{u}}}} \mathord{\left/ {\vphantom {{{{\Delta }}{\varepsilon _{\text{u}}}} 2}} \right. } 2}} \right) $ %Table 5.
$ \left( {{{{{\Delta }}{\varepsilon _{\text{u}}}} \mathord{\left/ {\vphantom {{{{\Delta }}{\varepsilon _{\text{u}}}} 2}} \right. } 2}} \right) $ of Funnel Sample Corresponding to$ \left( {{{{{\Delta }}{\varepsilon _{\text{t}}}} \mathord{\left/ {\vphantom {{{{\Delta }}{\varepsilon _{\text{t}}}} 2}} \right. } 2}} \right) $ $ \left( {{{{{\Delta }}{\varepsilon _{\text{t}}}} \mathord{\left/ {\vphantom {{{{\Delta }}{\varepsilon _{\text{t}}}} 2}} \right. } 2}} \right) $ 漏斗根部 $ {\varepsilon _{\text{e}}} $ $ {\varepsilon _{\text{p}}} $ $ \left( {{{{{\Delta }}{\varepsilon _{\text{u}}}} \mathord{\left/ {\vphantom {{{{\Delta }}{\varepsilon _{\text{u}}}} 2}} \right. } 2}} \right) $ 0.1 0.19 0 0.19 0.2 0.34 0.02 0.36 0.3 0.36 0.37 0.73 0.4 0.39 0.85 1.24 0.5 0.40 1.33 1.73 0.6 0.41 1.77 2.19 0.7 0.42 2.20 2.62 0.8 0.43 2.62 3.05 0.9 0.44 3.03 3.47 1.0 0.45 3.43 3.88 1.1 0.45 3.83 4.28
下载: 导出CSV
-
[1] 李顺平,彭倩,杨忠波,等. Zr-Sn-Nb合金薄板焊后组织和力学性能研究[J]. 核动力工程,2017, 38(4): 149-152. doi: 10.13832/j.jnpe.2017.04.0149 [2] WISNER S B, REYNOLDS M B, ADAMSON R B. Fatigue behavior of irradiated and unirradiated zircaloy and zirconium[C]//Proceedings of the International Symposium on Zirconium in the Nuclear Industry. Baltimore, 1994: 499. [3] 黄学伟,蔡力勋,包陈,等. Zr-Sn-Nb薄片合金高温低周疲劳行为[J]. 原子能科学技术,2010, 44(1): 60-64. [4] 贾琦,蔡力勋,包陈. 考虑循环塑性修正的薄片材料低周疲劳试验方法[J]. 工程力学,2014, 31(1): 218-233. doi: 10.6052/j.issn.1000-4750.2010.12.0920 [5] 李聪. 锆合金的低周疲劳行为研究[D]. 成都: 四川大学, 2003. [6] 田锋,李中奎,张建军,等. Zr-Sn-Nb合金焊接接头的应变疲劳特性[J]. 稀有金属材料与工程,2011, 40(12): 2188-2192. [7] 李顺平, 彭倩, 陈乐. Zr-Sn-Nb合金薄板焊接接头低周疲劳性能研究[C]//中国力学大会论文集（CCTAM 2019）. 杭州: 中国力学学会, 2019. -
计量
- 文章访问数: 71
- HTML全文浏览量: 12
- PDF下载量: 15
- 被引次数: 0
