核电阀门管系高保真动力学模型修正技术研究

薛睿渊; 张永楠; 张希恒; 俞树荣; 孟晓桥; 余建平

doi:10.13832/j.jnpe.2024.01.0130

核电阀门管系高保真动力学模型修正技术研究

doi: 10.13832/j.jnpe.2024.01.0130

兰州理工大学石油化工学院，兰州，730050

基金项目: 甘肃省青年科技基金计划（22JR5RA297）

详细信息

作者简介:
薛睿渊（1993—），男，博士研究生，副教授，硕士研究生导师，现主要从事核电阀门抗震设计与分析，E-mail: xrywyy@163.com

中图分类号: O327；TL37
计量
- 文章访问数: 103
- HTML全文浏览量: 21
- PDF下载量: 24
- 被引次数: 0
出版历程
- 收稿日期: 2023-06-20
- 修回日期: 2023-11-28
- 刊出日期: 2024-02-15

Research on High-fidelity Dynamic Model Updating Technology of Nuclear Power Valve Piping System

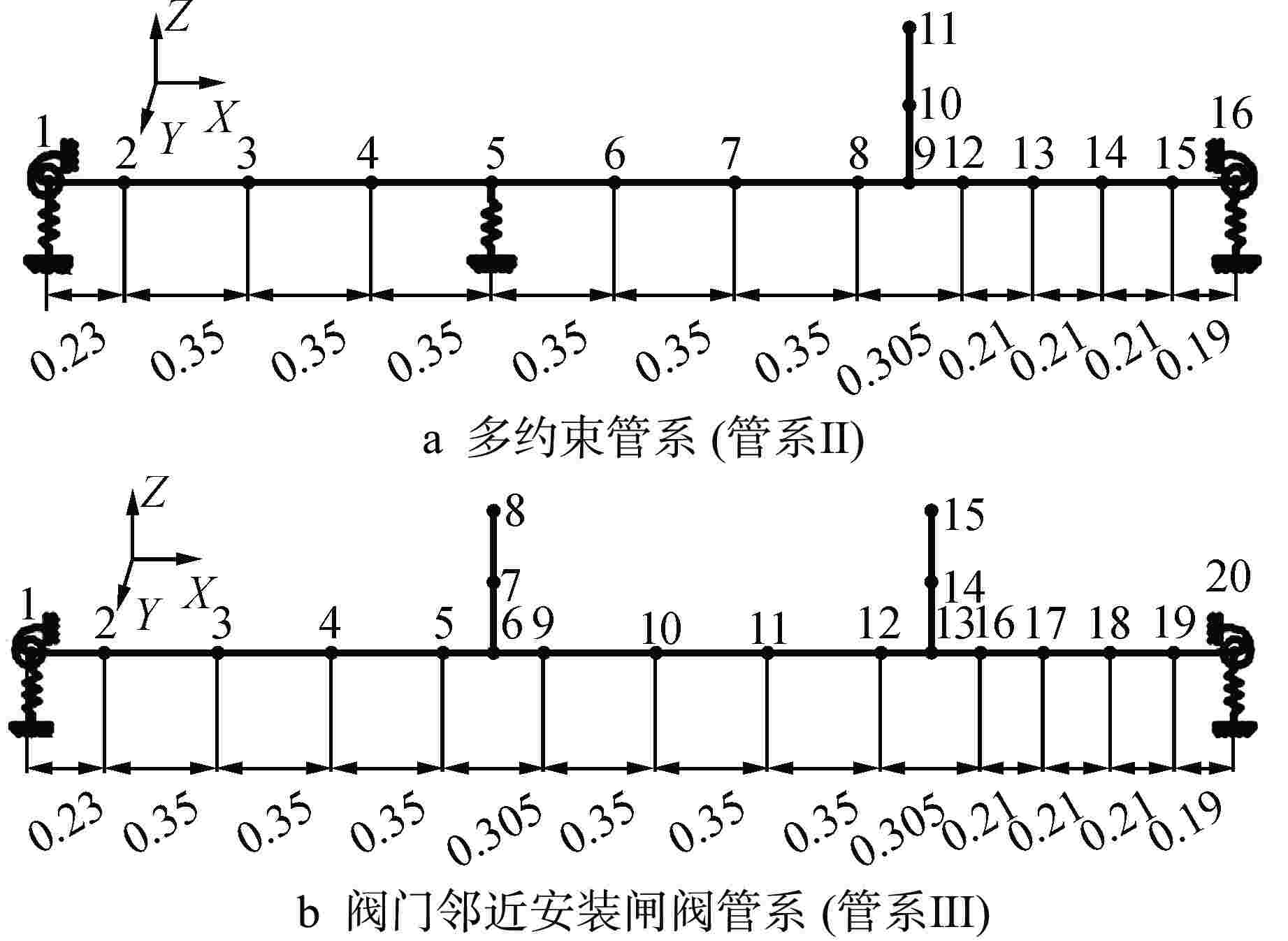
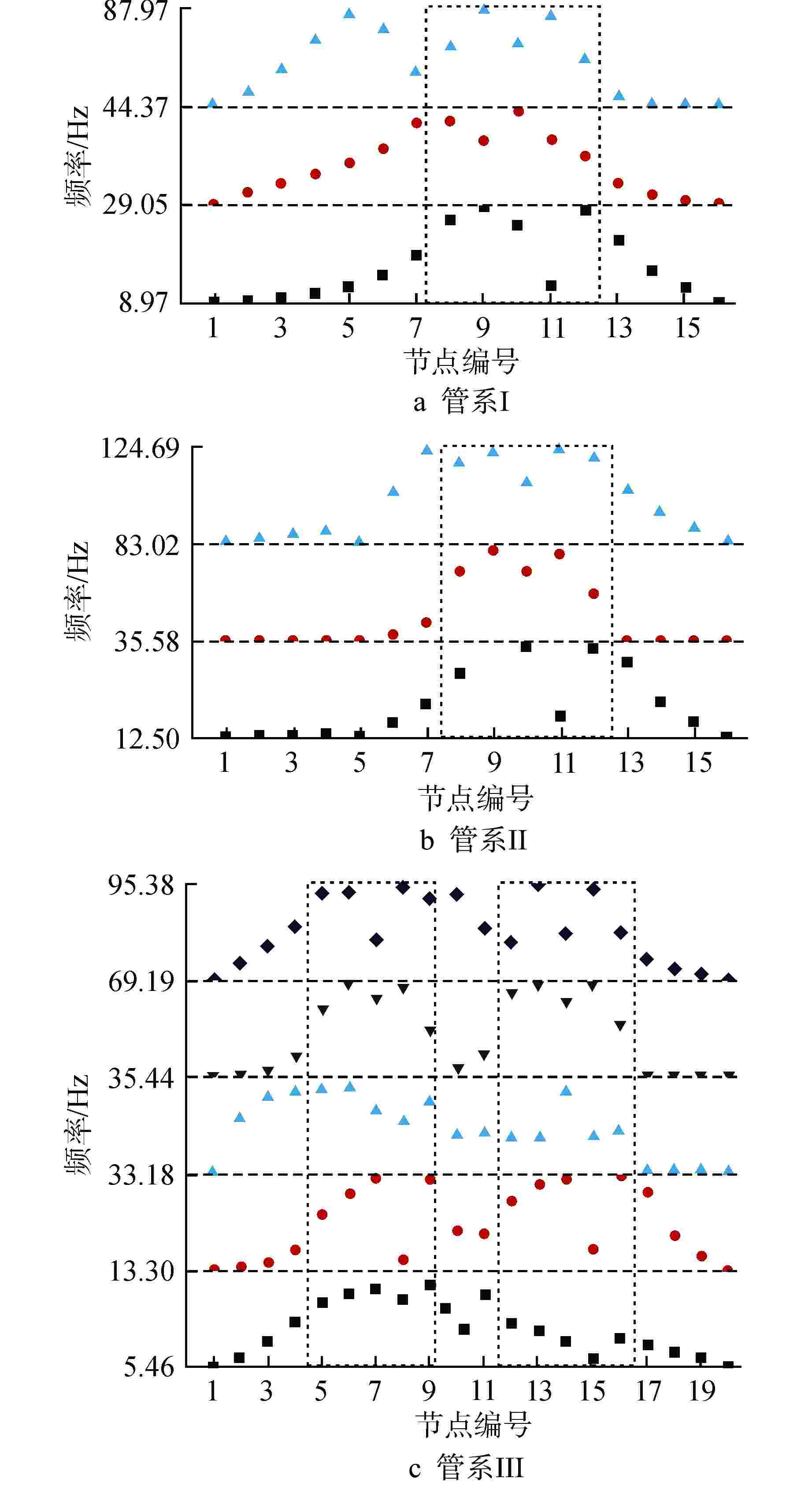
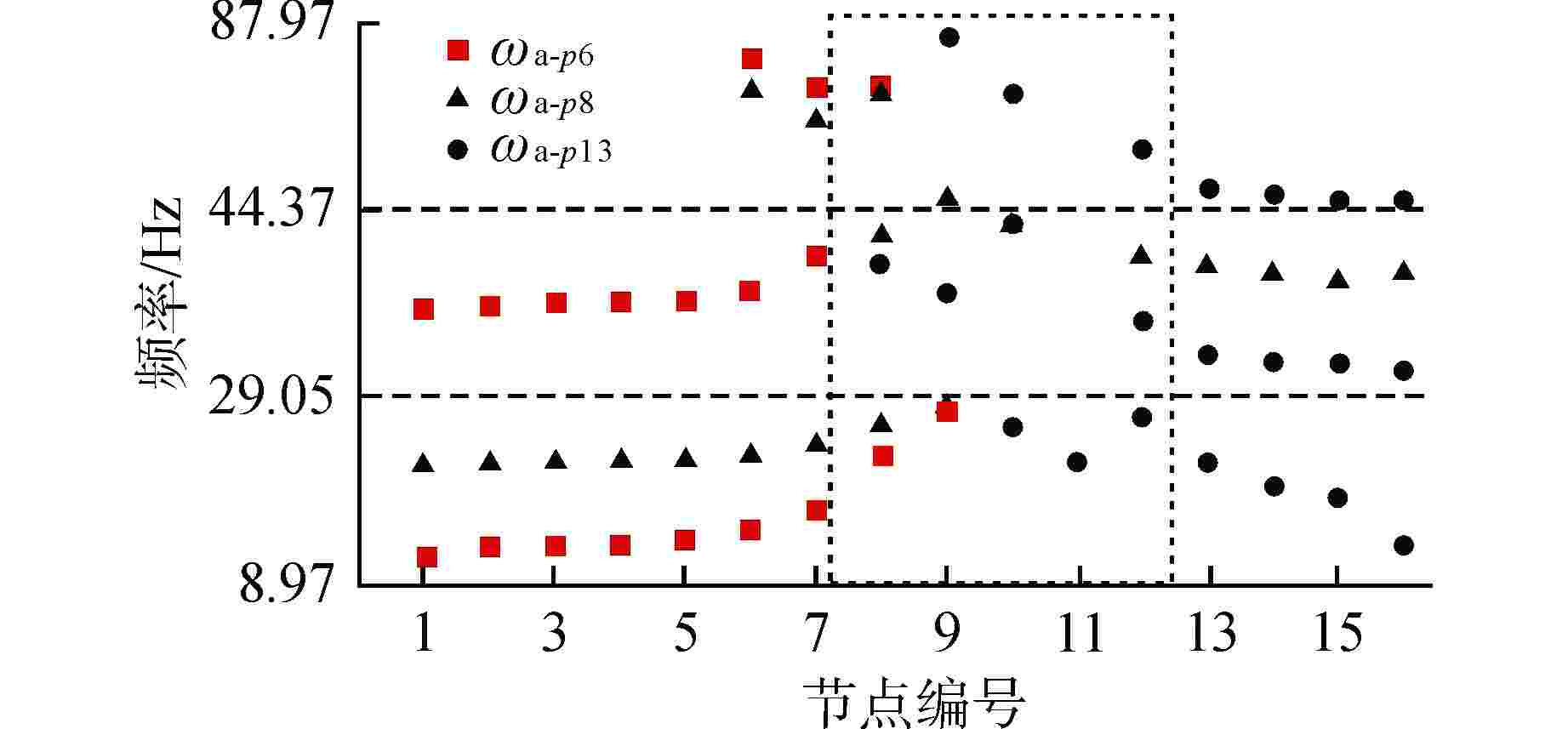
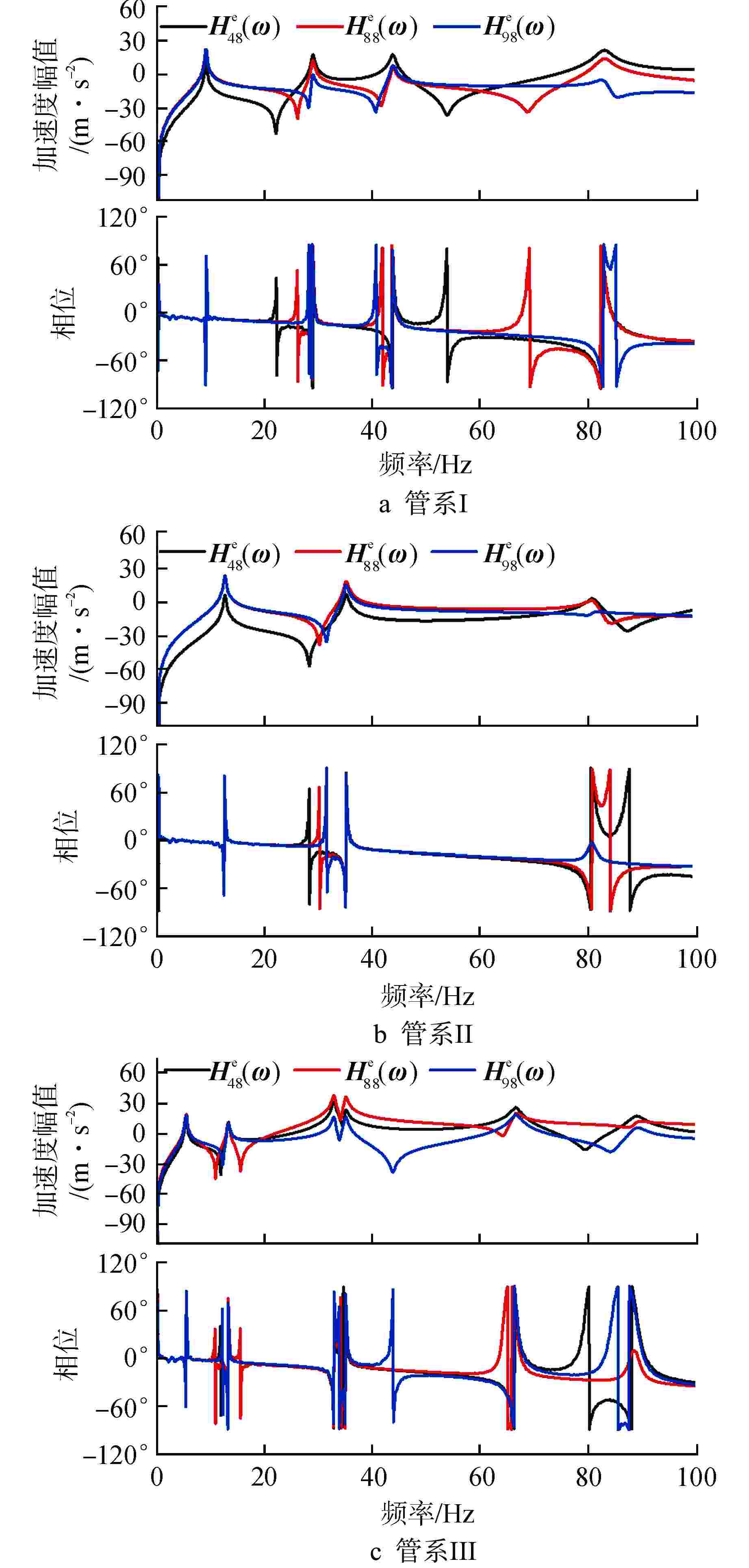
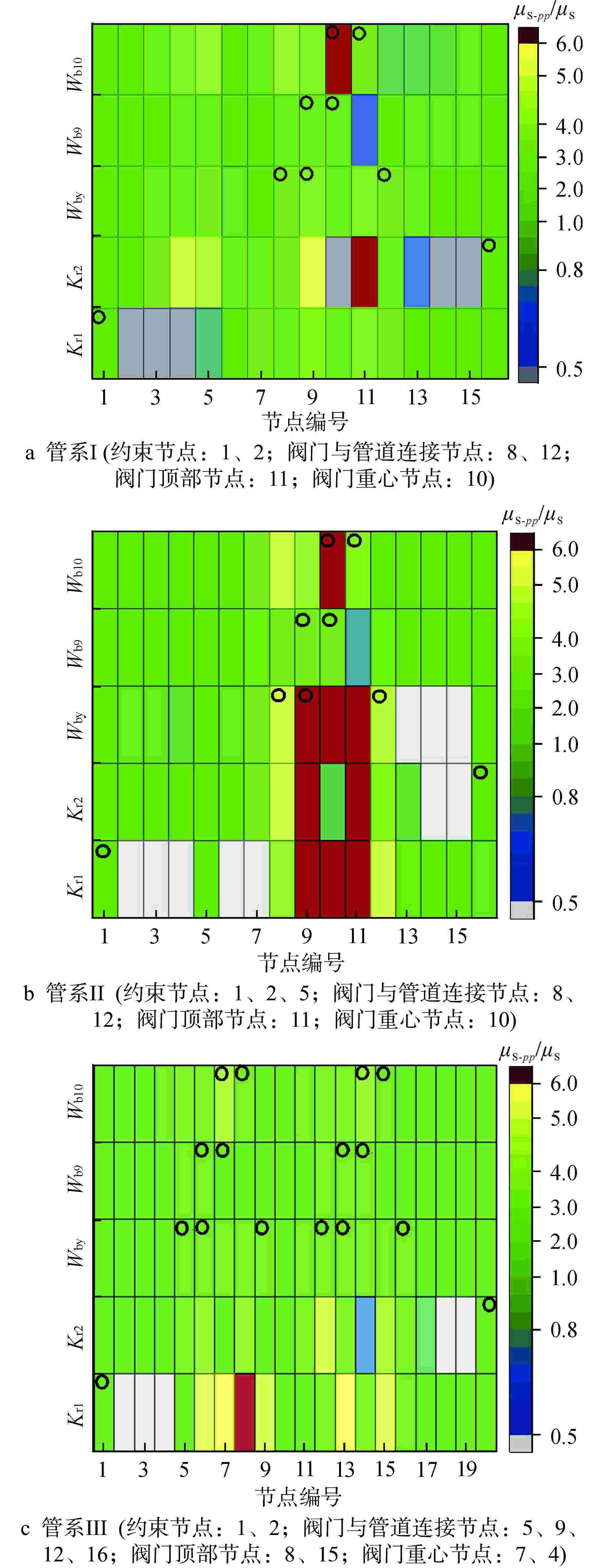
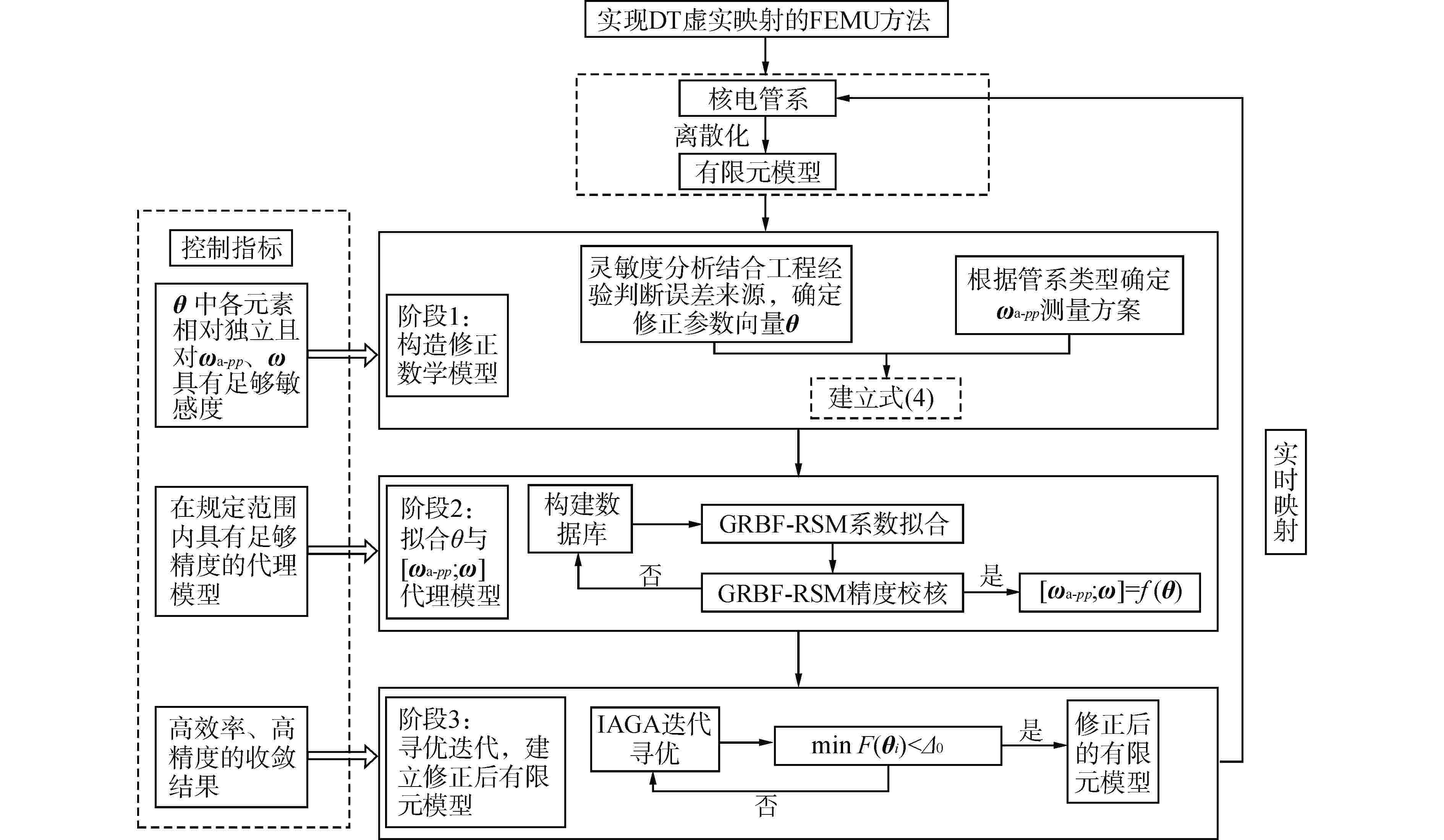
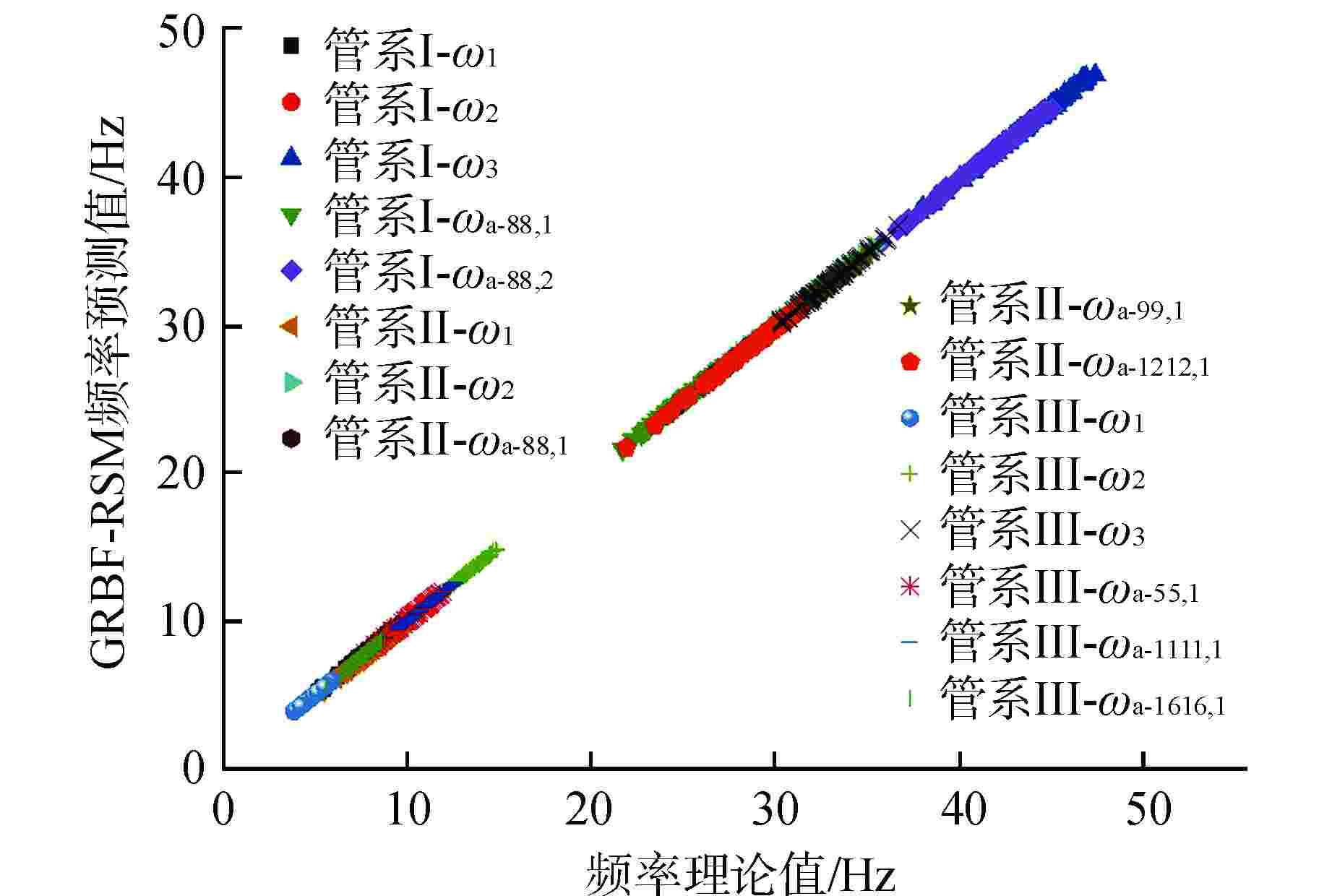
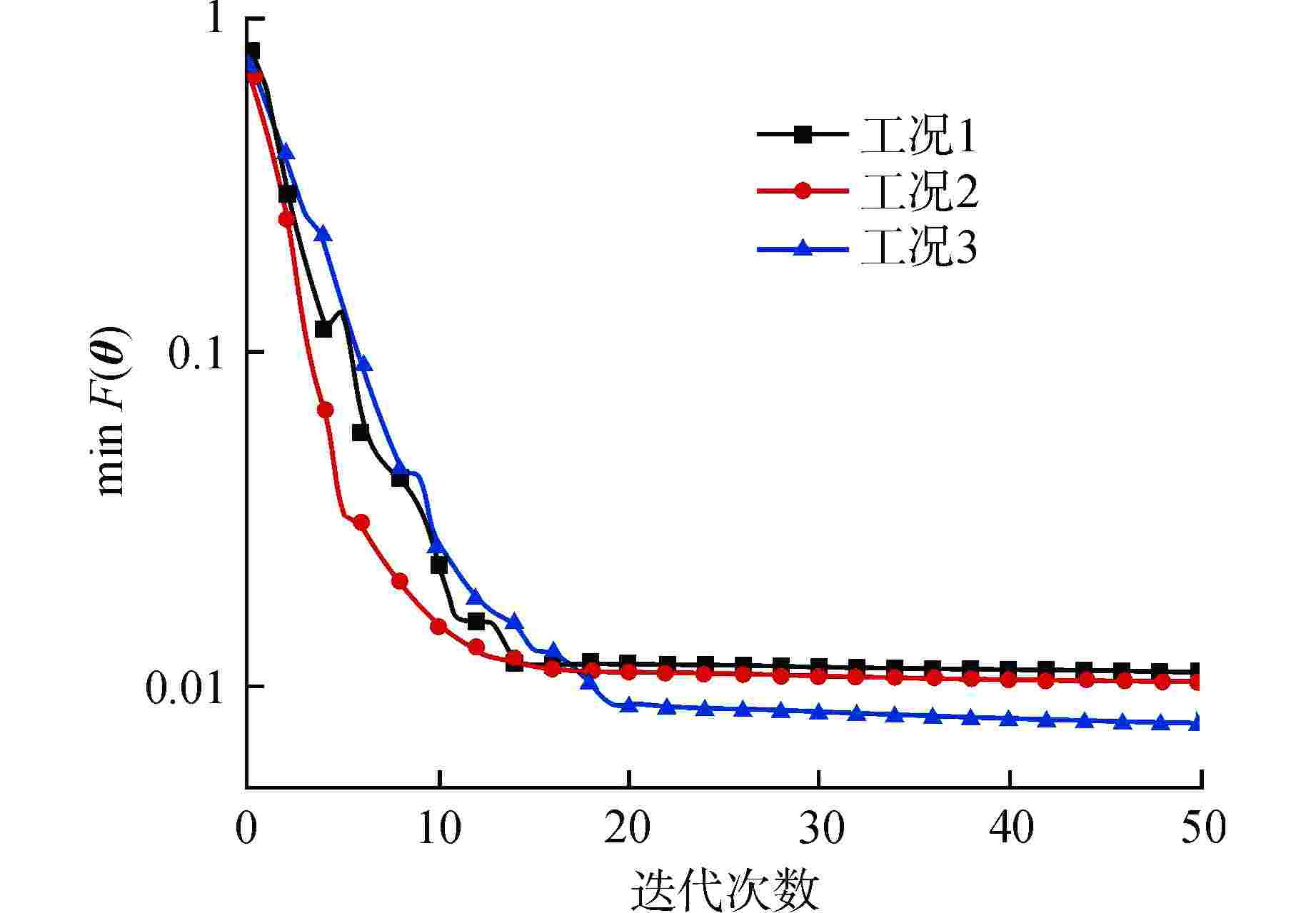
School of Petrochemical Engineering, Lanzhou University of Technology, Lanzhou, 730050, China

摘要

摘要: 高保真动力学模型是在役核电阀门管系抗震裕度分析、抗震性能监测、抗震设计持续改进的基础，然而其建立过程面临着难度大、效率低的问题。基于某实际阀门管系高保真动力学模型对各类管系反共振频率特性开展研究，结果表明：核电阀门管系的原点反共振频率与共振频率交替出现，在低频区域，各类管系原点反共振频率的理论值与测量值匹配较好；在阀门与管道连接位置，不同结构参数对原点反共振频率和共振频率有较为接近的灵敏度，实际工程中应优先在此位置布置测点。以此为理论基础，以共振频率与反共振频率共同作为目标函数，提出了结合高斯径向基响应面与自适应遗传算法的有限元模型修正方法。实际算例表明，提出的方法克服了试验数据不足、收敛速度慢的难点，能够高精度、高效率地识别阀门管系中的未知结构参数，建立其高保真动力学模型。研究成果为核电阀门管系抗震设计经济性和安全性的进一步提升提供了可能。
- 核级阀门管系 /
- 反共振频率 /
- 频响函数 /
- 模型修正
Abstract: The high-fidelity dynamic model is the basis for seismic margin analysis, seismic performance monitoring and continuous improvement of seismic design of in-service nuclear power valve piping system. However, its establishment process is faced with the problems of great difficulty and low efficiency. Based on the high-fidelity dynamic model of a practical valve piping system, the anti-resonance frequency characteristics of various piping systems are studied. The results show that the origin anti-resonance frequency and the resonance frequency appear alternately. In the low frequency region, the theoretical values of the origin anti-resonance frequency of various piping systems match the measured values well. At the connection position between the valve and the pipeline, different structural parameters have close sensitivity to the origin anti-resonance frequency and resonance frequency, so the measuring points should be preferentially arranged at these positions in practical engineering. Based on this theory, a finite element model updating method combining Gaussian Radial Basis Function-Response Surface Method and Improved Adaptive Genetic Algorithm is proposed with resonance frequency and anti-resonance frequency as the objective function. The example shows that the proposed method overcomes the difficulties of insufficient test data and slow convergence speed, and can identify the unknown structural parameters in nuclear valve piping with high precision and high efficiency, as well as establishes its high-fidelity dynamic model. The research results provide the possibility for further improvement of the economy and safety of seismic design of nuclear power valve piping system.
- Nuclear grade valve piping system /
- Anti-resonance frequencies /
- Frequency response function /
- Model updating

HTML全文

图 1 集中质量有限元模型及其误差来源　单位：m

Figure 1. Lumped Mass FEM and Error Sources

下载: 全尺寸图片幻灯片

图 2 不同管系集中质量有限元模型

Figure 2. Lumped Mass FEMs for Different Pipe Systems

下载: 全尺寸图片幻灯片

图 3 原点反共振频率分布

Figure 3. Origin Antiresonance Frequency Distribution

下载: 全尺寸图片幻灯片

图 4 管系Ⅰ跨点反共振频率分布

Figure 4. Transfer Antiresonance Frequency Distribution of Pipe System Ⅰ

下载: 全尺寸图片幻灯片

图 5 频率响应函数Bode图

Figure 5. Bode Plot of Frequency Response Function

下载: 全尺寸图片幻灯片

图 6 修正参数对ω及ω_a-pp灵敏度偏差云图

Figure 6. Sensitivity Deviation Cloud Map of Updating Parameters for ω and ω_a-pp

下载: 全尺寸图片幻灯片

图 7 适用于DT虚实映射FEMU方法流程

Δ₀—迭代终止条件

Figure 7. FEMU Flow for DT Virtual Real Mapping

下载: 全尺寸图片幻灯片

图 8 GRBF-RSM拟合结果

Figure 8. Curve Fitting by GRBF-RSM

下载: 全尺寸图片幻灯片

图 9 修正过程收敛曲线

Figure 9. Convergence Curve of Updating Process

下载: 全尺寸图片幻灯片

图 10 修正前后H₈₈(ω)幅频曲线对比

Figure 10. Comparison of H₈₈(ω) Amplitude-Frequency Curves before and after Correction

下载: 全尺寸图片幻灯片

表 1 修正工况详情

Table 1. Updating Condition Details

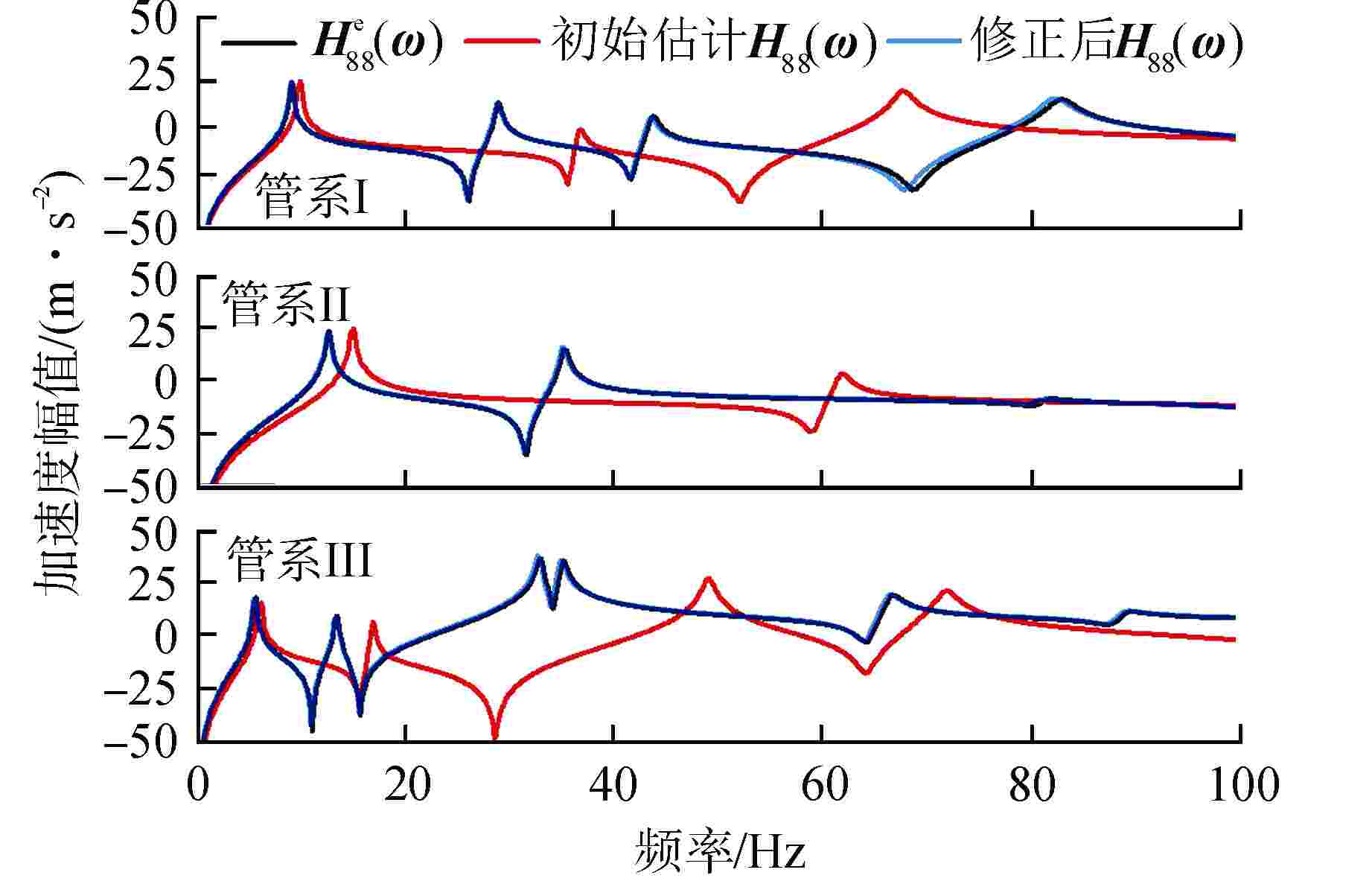
工况	适用对象	模拟实测数据
1	管系Ⅰ	ω₁、ω₂、ω₃、ω_a-88,1、ω_a-88,2
2	管系Ⅱ	ω₁、ω₂、ω_a-88,1、ω_a-99,1、ω_a-1212,1
3	管系Ⅲ	ω₁、ω₂、ω₃、ω_a-55,1、ω_a-1111,1、ω_a-1616,1

下载: 导出CSV

表 2 修正结果与偏差

Table 2. Updating Results and Deviations

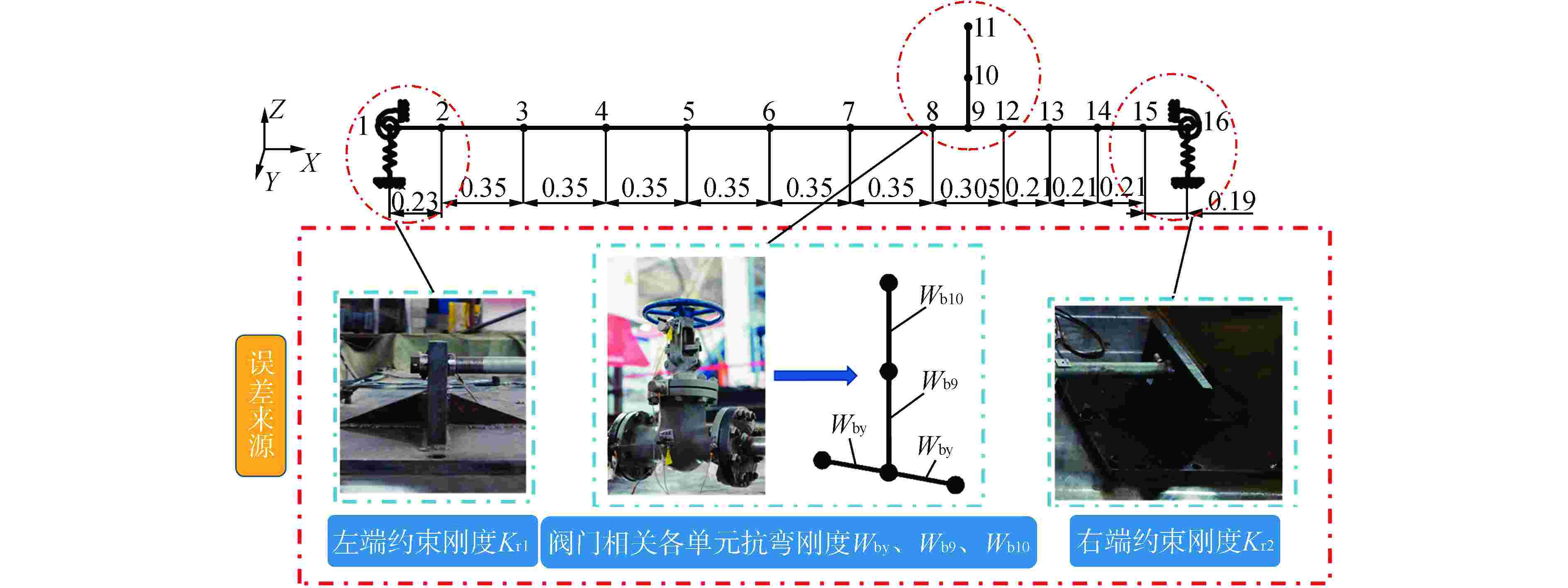
工况	K_r1		K_r2		W_by		W_b9		W_b10
工况	修正值/(N·m·rad⁻¹)	偏差/%	修正值/(N·m·rad⁻¹)	偏差/%	修正值/(N·m⁶)	偏差/%	修正值/(N·m⁶)	偏差/%	修正值/(N·m⁶)	偏差/%
1	1.57×10⁵	4.58	1.48×10⁵	0.41	1.84×10⁴	0.45	4.31×10³	2.36	2.16×10³	2.31
2	1.56×10⁵	4.67	1.43×10⁵	3.09	1.90×10⁴	0.99	4.31×10³	2.88	2.17×10³	3.73
3	1.50×10⁵	3.80	1.44×10⁵	0.94	1.83×10⁴	0.17	4.15×10³	1.41	2.09×10³	1.41

下载: 导出CSV

参考文献(25)

[1]	LAL K M, PARSI S S, KOSBAB B D, et al. Towards standardized advanced nuclear reactors: seismic isolation and the impact of the earthquake load case[J]. Nuclear Engineering and Design, 2022, 386: 111487.
[2]	谭思超,李桐,刘永超,等. 关于人工智能在核能领域应用的若干思考[J]. 核动力工程,2023, 44(2): 1-8.
[3]	SEMERARO C, LEZOCHE M, PANETTO H, et al. Digital twin paradigm: a systematic literature review[J]. Computers in Industry, 2021, 130: 103469.
[4]	陶飞,刘蔚然,张萌,等. 数字孪生五维模型及十大领域应用[J]. 计算机集成制造系统,2019, 25(1): 1-18.
[5]	陶飞,张贺,戚庆林,等. 数字孪生十问: 分析与思考[J]. 计算机集成制造系统,2020, 26(1): 1-17.
[6]	熊夫睿,叶献辉. 模态应变能在反应堆及一回路系统动力分析中的应用[J]. 核动力工程,2019, 40(3): 205-210.
[7]	熊夫睿,沈平川,王新军,等. 华龙一号反应堆冷却剂系统抗震设计关键技术[J]. 原子能科学技术,2022, 56(S1): 83-91.
[8]	黄茜,熊夫睿,王碧浩,等. 地震载荷下反应堆系统的不确定性量化[J]. 原子能科学技术,2019, 53(5): 899-905.
[9]	李开宇,蔡琦,才鑫馨,等. 数字孪生技术在浮动核电站设计阶段中的应用研究[J]. 核动力工程,2022, 43(1): 197-201.
[10]	龚禾林,陈长,李庆,等. 基于物理指引和数据增强的反应堆物理运行数字孪生研究[J]. 核动力工程,2021, 42(S2): 48-53.
[11]	GONG H L, ZHU T, CHEN Z, et al. Parameter identification and state estimation for nuclear reactor operation digital twin[J]. Annals of Nuclear Energy, 2023, 180: 109497. doi: 10.1016/j.anucene.2022.109497
[12]	GONG H L, CHENG S B, CHEN Z, et al. Data-enabled physics-informed machine learning for reduced-order modeling digital twin: application to nuclear reactor physics[J]. Nuclear Science and Engineering, 2022, 196(6): 668-693. doi: 10.1080/00295639.2021.2014752
[13]	陈静,卢燕臻,江灏,等. 基于孪生模型的堆芯自给能中子探测器信号异常检测[J]. 核动力工程,2023, 44(3): 210-216.
[14]	熊夫睿,张文正,袁志豪. 一回路系统整体支承结构多保真度力学模型的配型和更新研究[J]. 核动力工程,2023, 44(3): 243-248.
[15]	闫天红,王维刚,赵海峰,等. 现役导管架平台结构监测系统开发与数字孪生技术[J]. 中国机械工程,2021, 32(20): 2508-2513.
[16]	史英沙,黎胜. 多激励下结构反共振频率的计算和配置[J]. 振动工程学报,2023, 36(5): 1244-1250. doi: 10.16385/j.cnki.issn.1004-4523.2023.05.007
[17]	史英沙,黎胜. 船体梁振动的反共振频率配置设计[J]. 振动与冲击,2021, 40(3): 133-138,164.
[18]	胡海岩. 论线性系统的反共振问题[J]. 动力学与控制学报,2018, 16(5): 385-390.
[19]	HANSON D, WATERS T P, THOMPSON D J, et al. The role of anti-resonance frequencies from operational modal analysis in finite element model updating[J]. Mechanical Systems and Signal Processing, 2007, 21(1): 74-97. doi: 10.1016/j.ymssp.2006.01.001
[20]	费庆国,张令弥,李爱群,等. 基于不同残差的动态有限元模型修正的比较研究[J]. 振动与冲击,2005, 24(4): 24-26.
[21]	李家辉,许锋. 基于Kriging模型与MOGA算法的有限元模型修正[J]. 航空工程进展,2023, 14(4): 68-75.
[22]	陈乾,张沈习,程浩忠,等. 基于径向基函数随机响应面法的综合能源系统概率能流计算[J]. 中国电机工程学报,2022, 42(22): 8075-8088.
[23]	杨雅勋,柴文浩,杨福利,等. 基于加权响应面法和混沌粒子群优化算法的单梁有限元模型修正[J]. 兰州大学学报: 自然科学版,2021, 57(6): 823-829.
[24]	ZHOU K, TANG J. Structural model updating using adaptive multi-response Gaussian process meta-modeling[J]. Mechanical Systems and Signal Processing, 2021, 147: 107121. doi: 10.1016/j.ymssp.2020.107121
[25]	XUE R Y, YU S R, ZHANG X H. Identification of parameters in 2D-FEM of valve piping system within NPP utilizing seismic response[J]. Computers, Materials & Continua, 2020, 65(1): 789-805.