反应堆用新型自感式棒位探测器涡流效应分析

张艺璇; 徐奇伟; 唐健凯; 刘彦霆; 黄思语; 罗凌雁

doi:10.13832/j.jnpe.2024.01.0156

反应堆用新型自感式棒位探测器涡流效应分析

doi: 10.13832/j.jnpe.2024.01.0156

1.
重庆大学输变电装备技术全国重点实验室，重庆，400044
2.
中国核动力研究设计院核反应堆系统设计技术重点实验室，成都，610213

详细信息

作者简介:
张艺璇（1996—），女，博士研究生，现从事棒位探测器电磁分析方面的研究，E-mail: Zhangyx@stu.cqu.edu.cn

中图分类号: TL363
计量
- 文章访问数: 99
- HTML全文浏览量: 15
- PDF下载量: 12
- 被引次数: 0
出版历程
- 收稿日期: 2023-03-16
- 修回日期: 2023-11-15
- 刊出日期: 2024-02-15

Eddy Current Effect Analysis of a New Self-sensing Rod Position Detector for Reactor

1.
State Key Laboratory of Power Transmission Equipment Technology, Chongqing University, Chongqing, 400044, China
2.
Science and Technology on Reactor System Design Technology Laboratory, Nuclear Power Institute of China, Chengdu, 610213, China

摘要

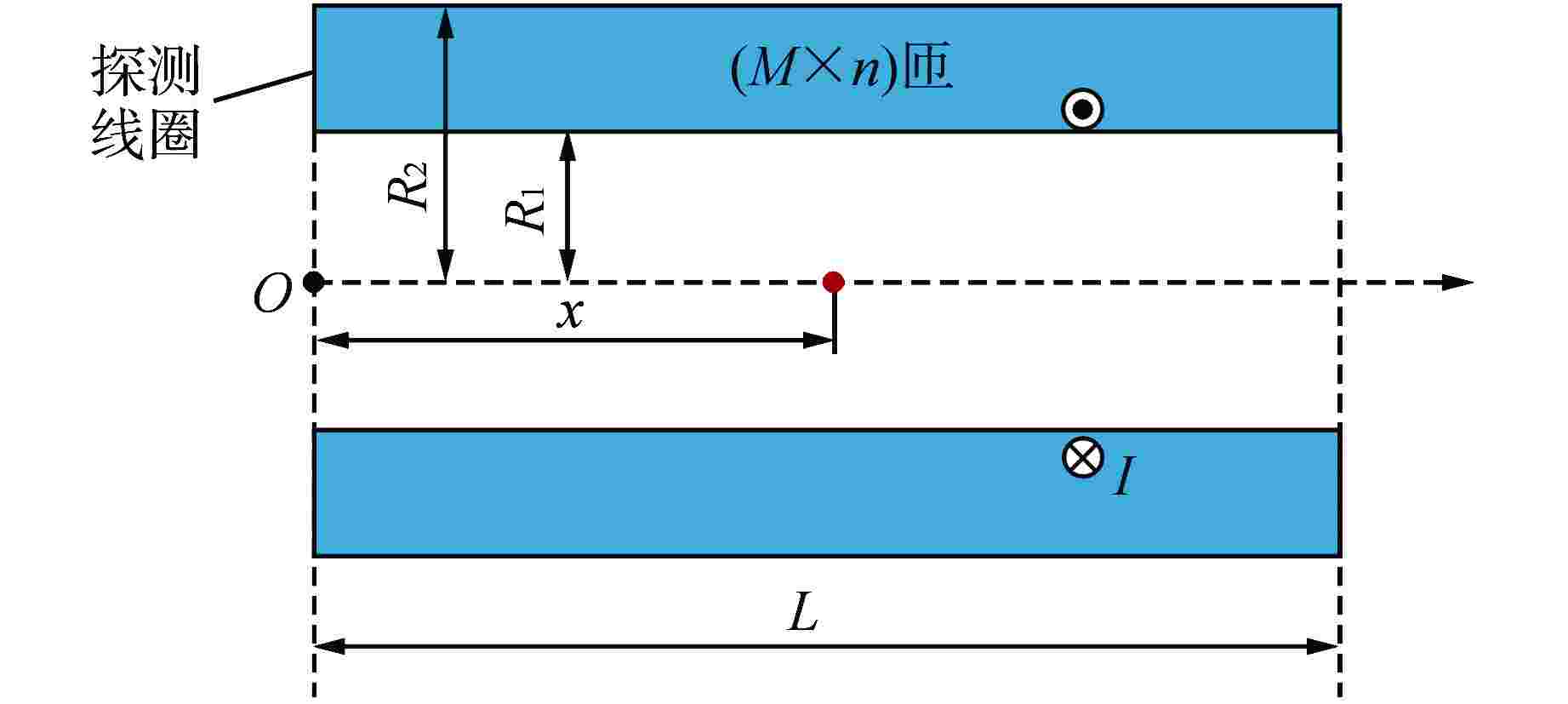
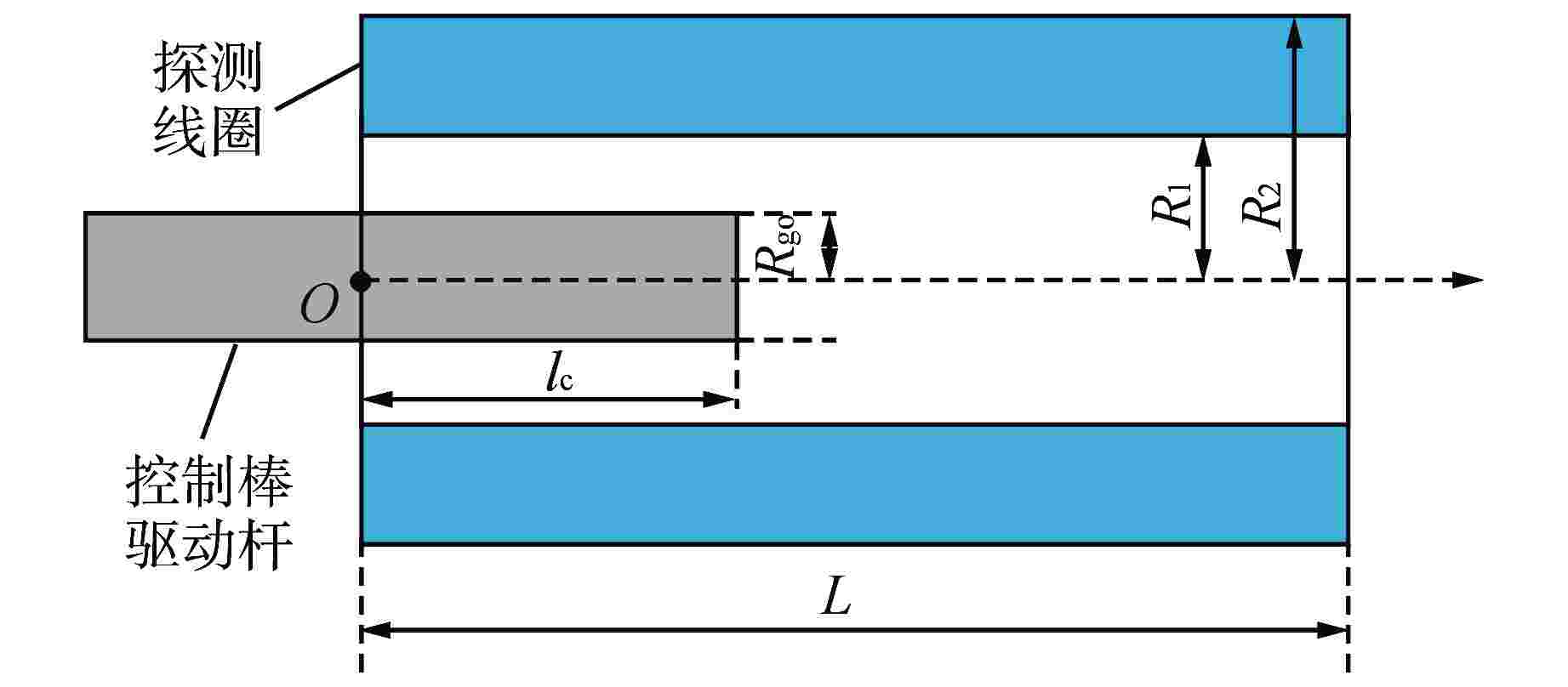
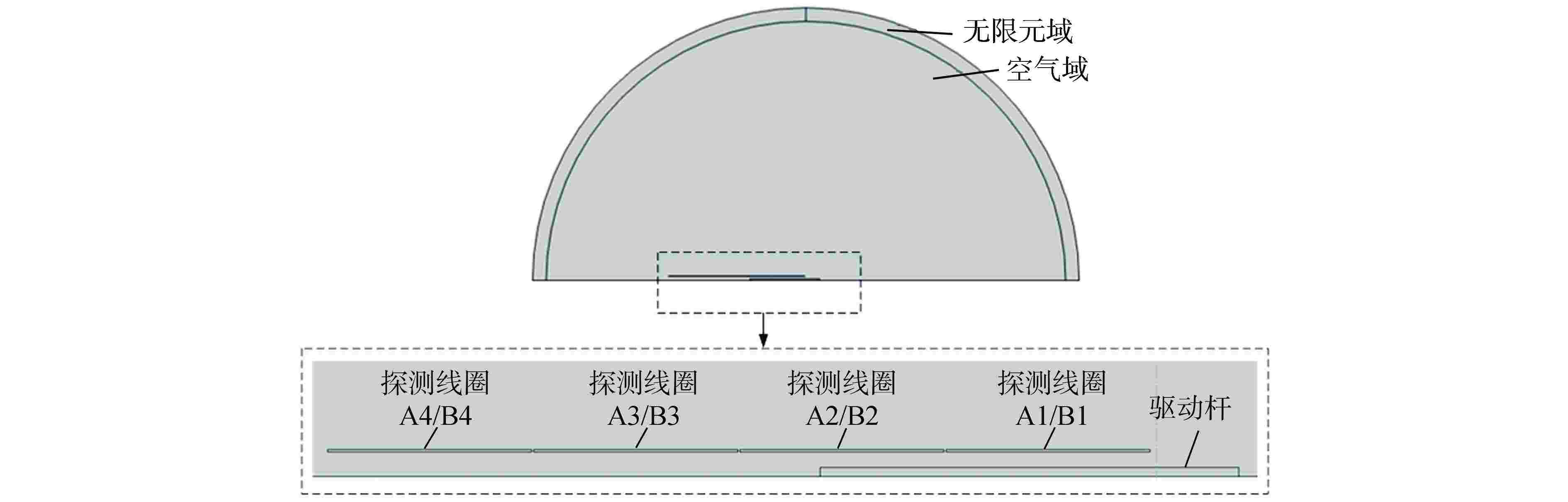
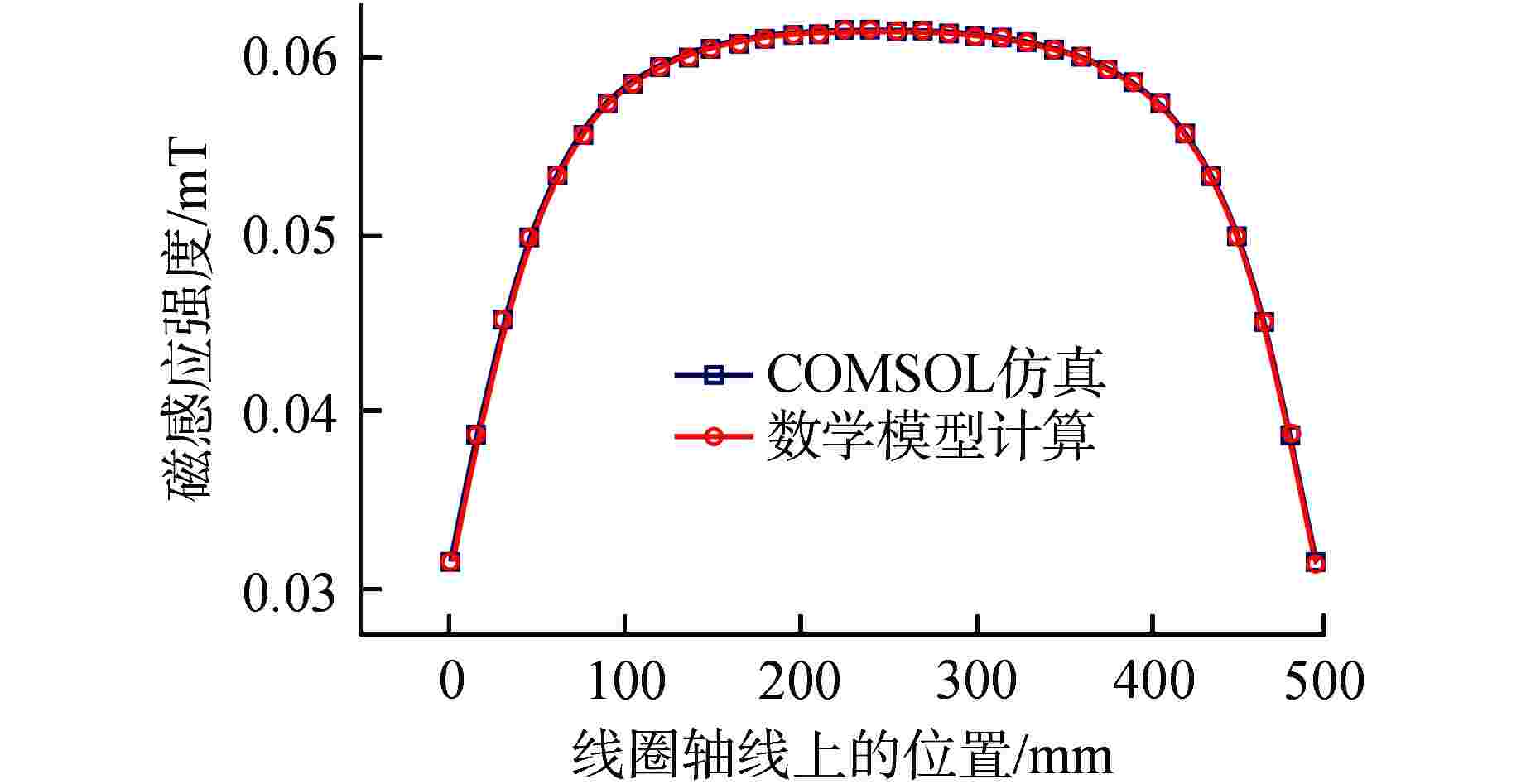
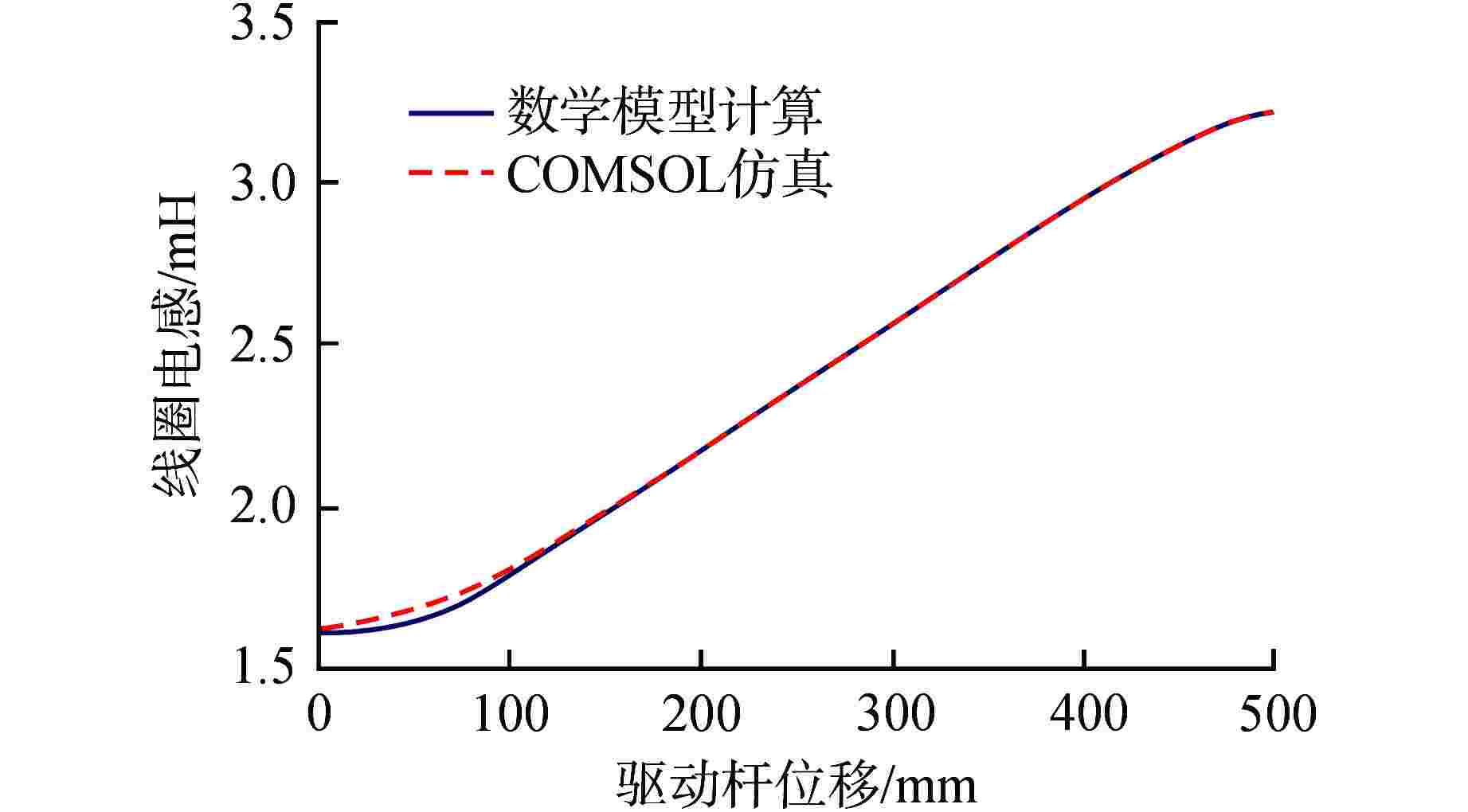
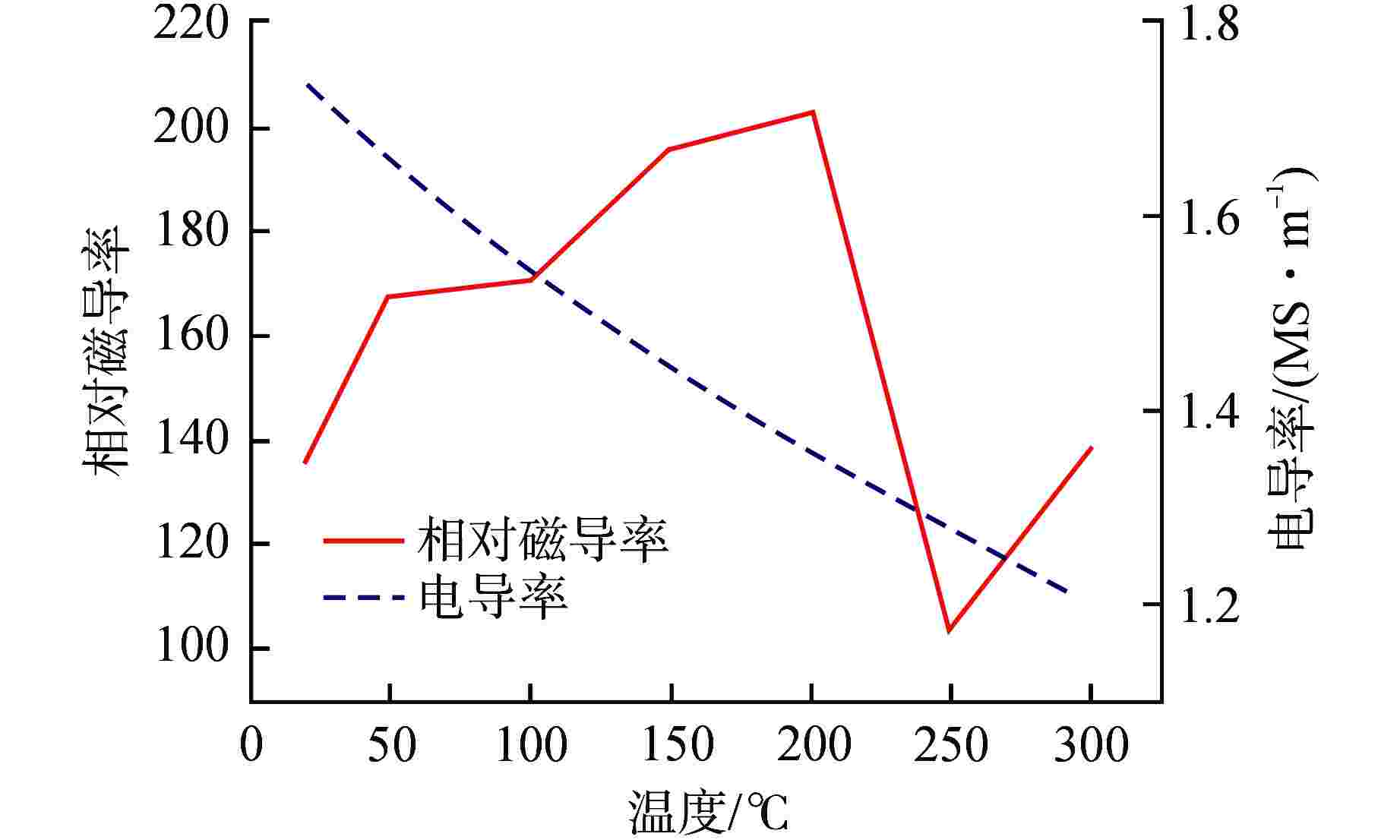
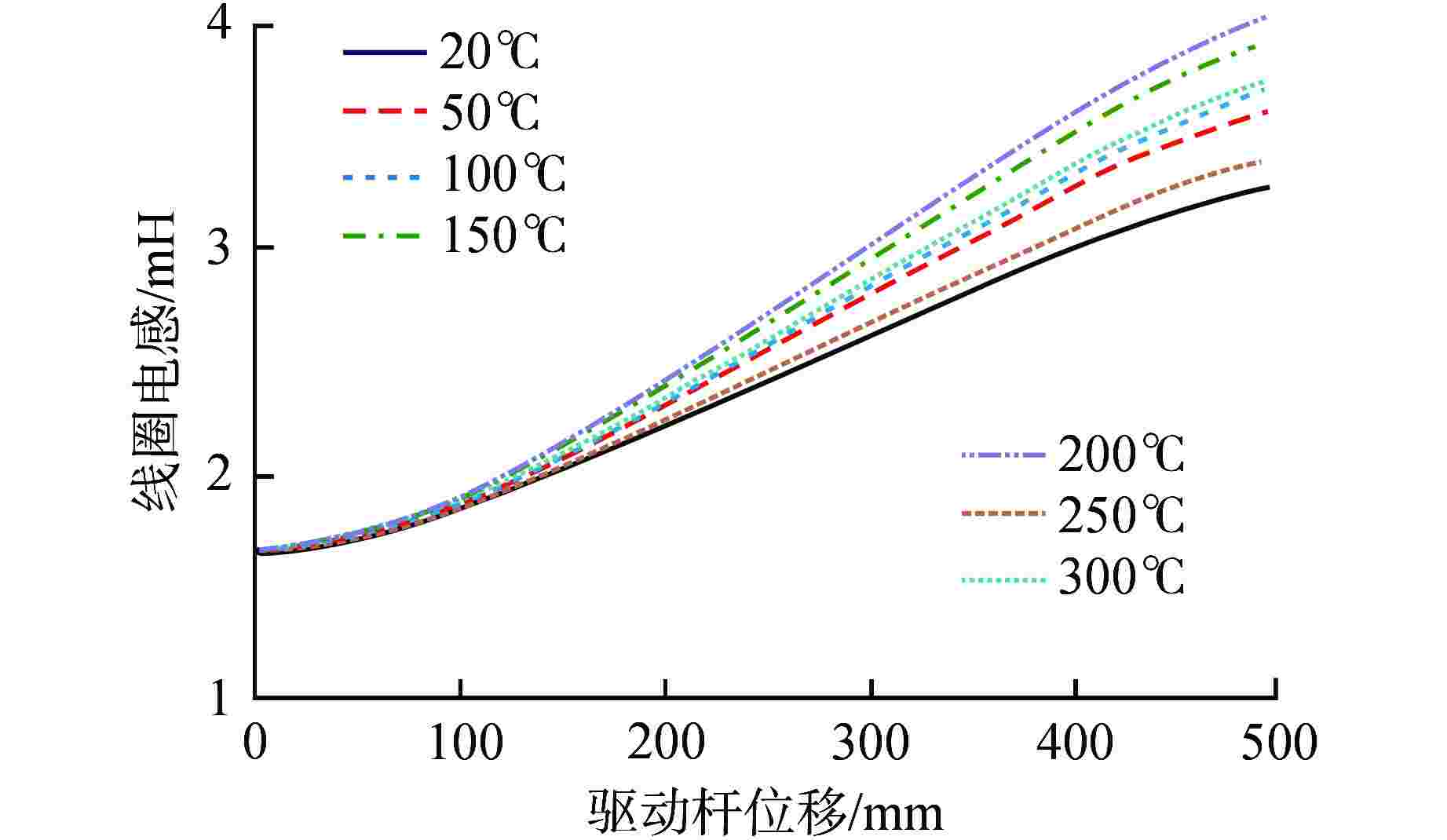
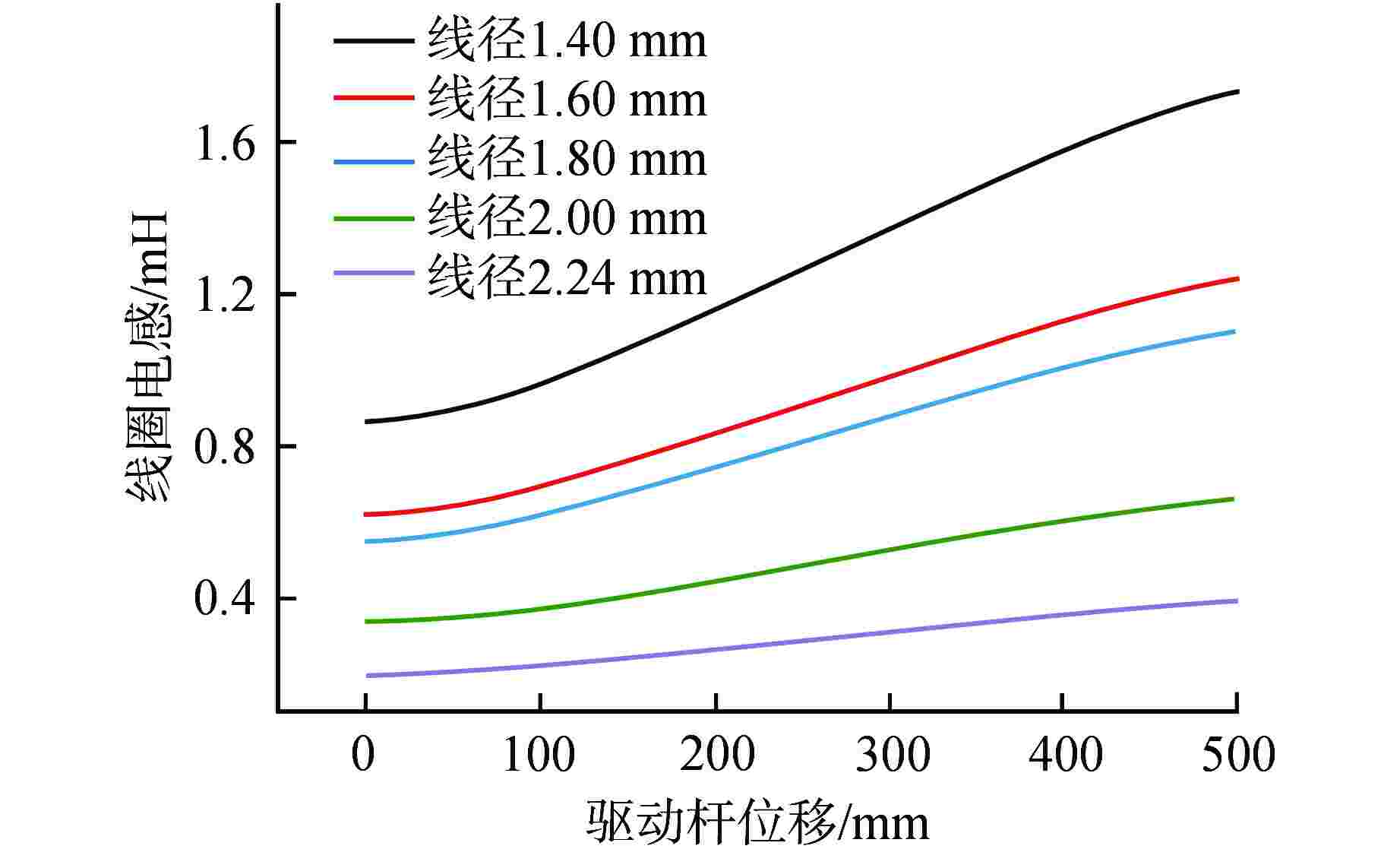
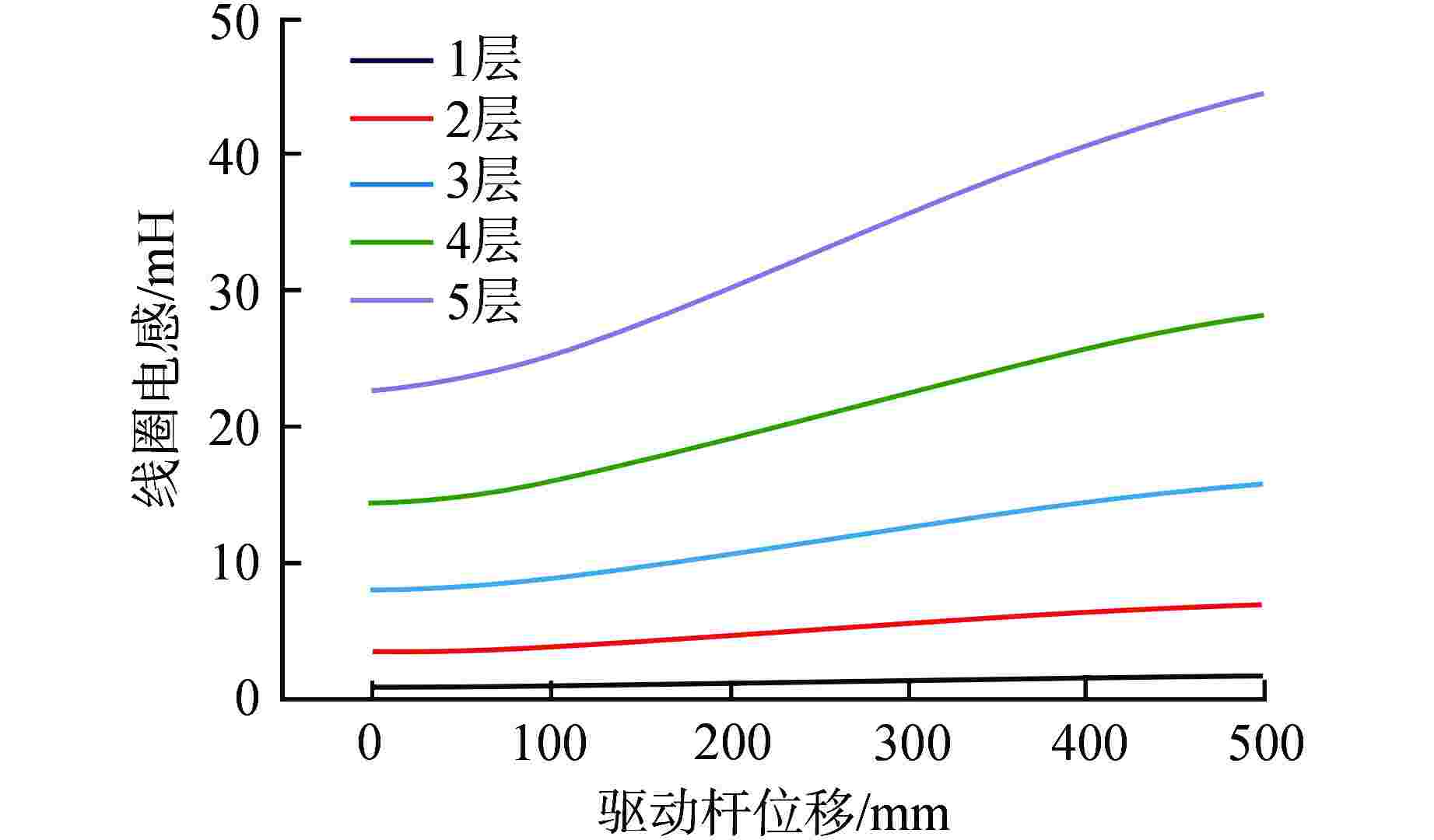
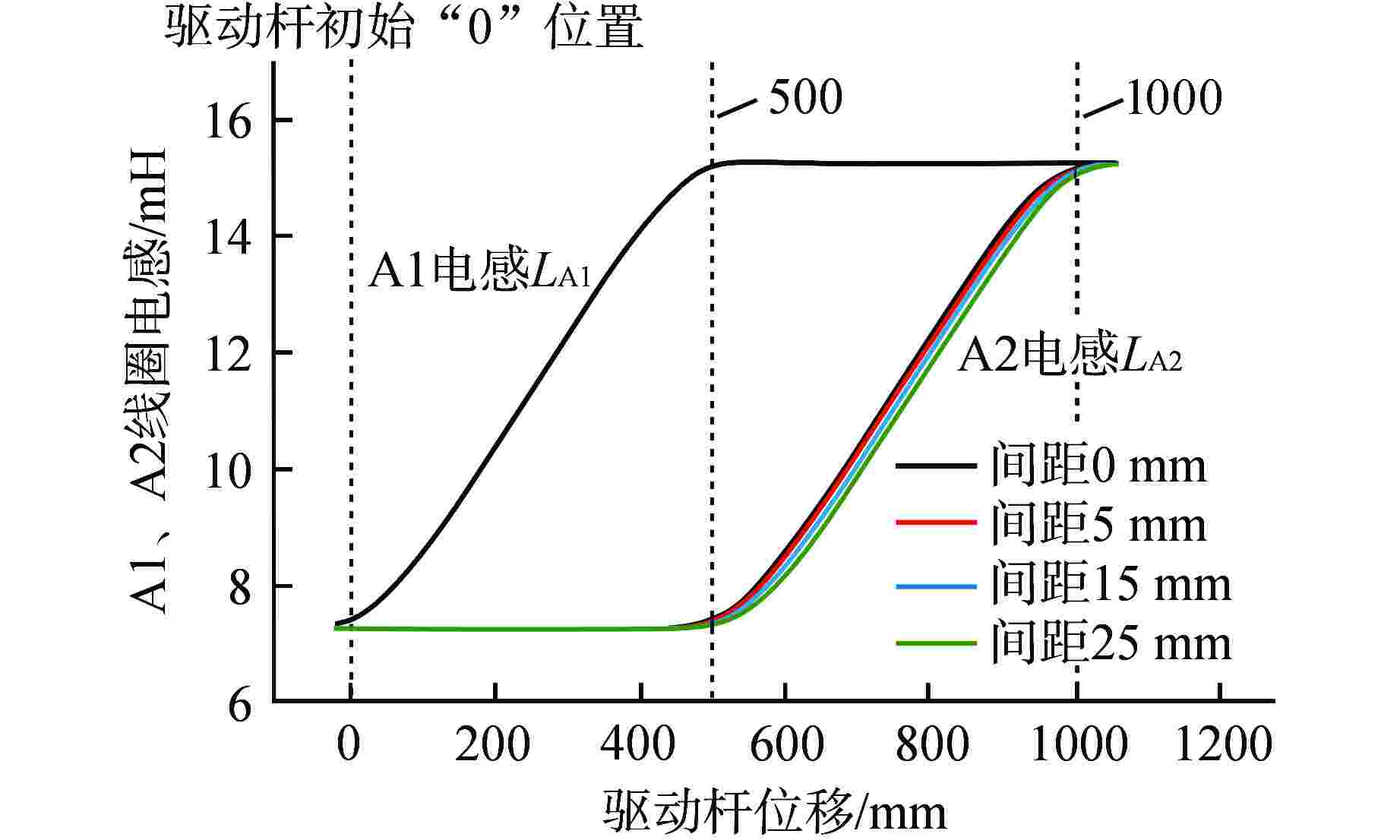
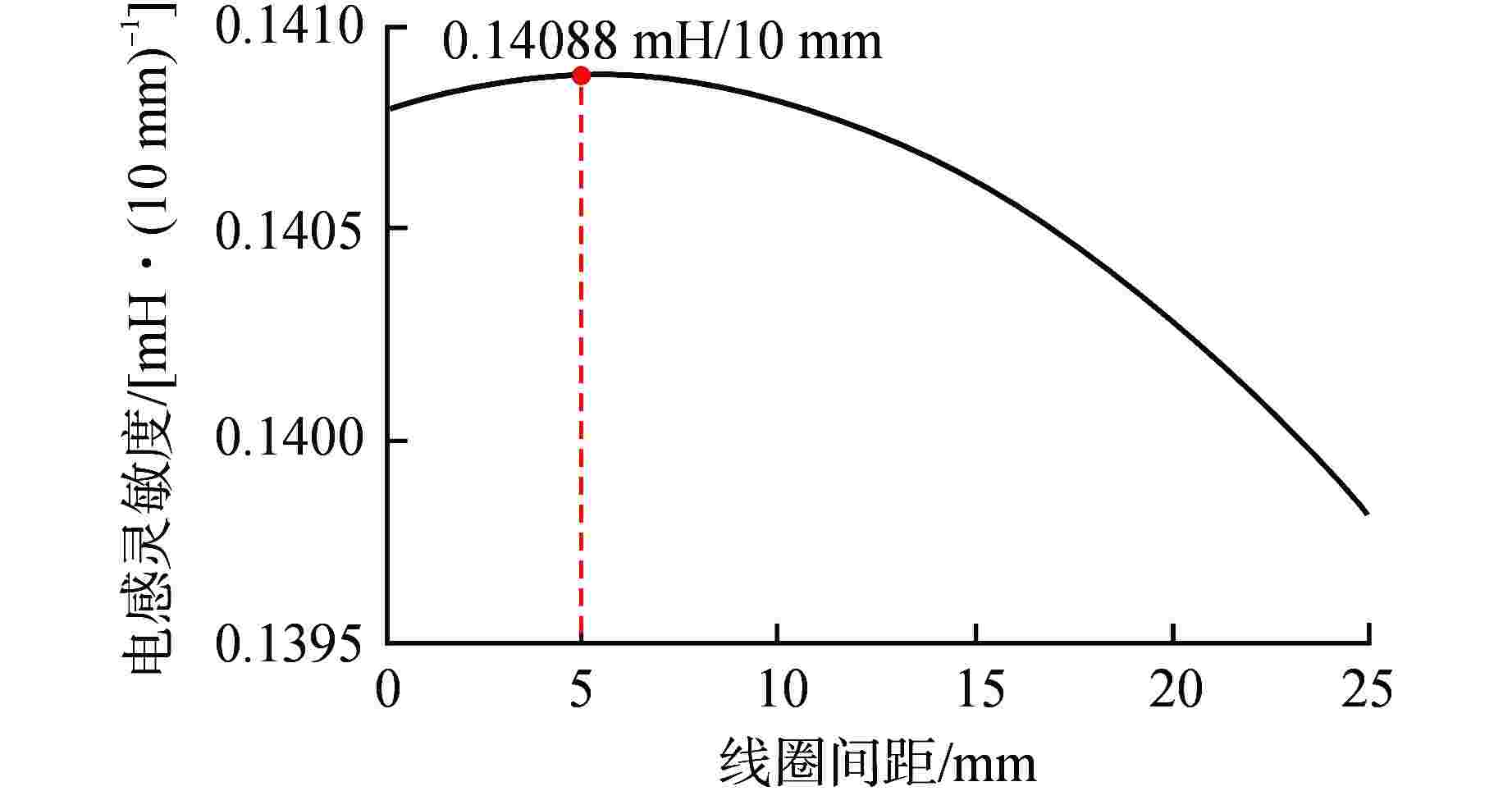
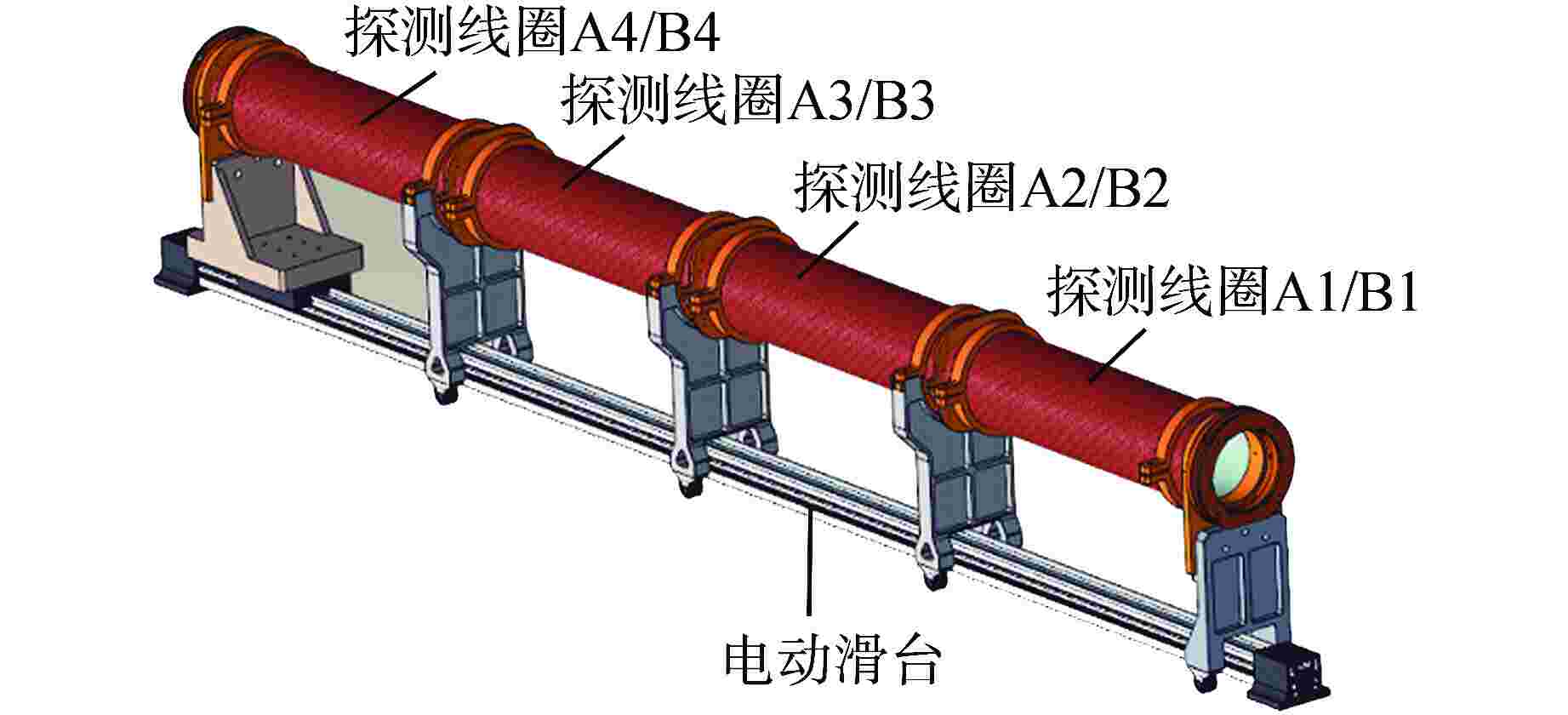
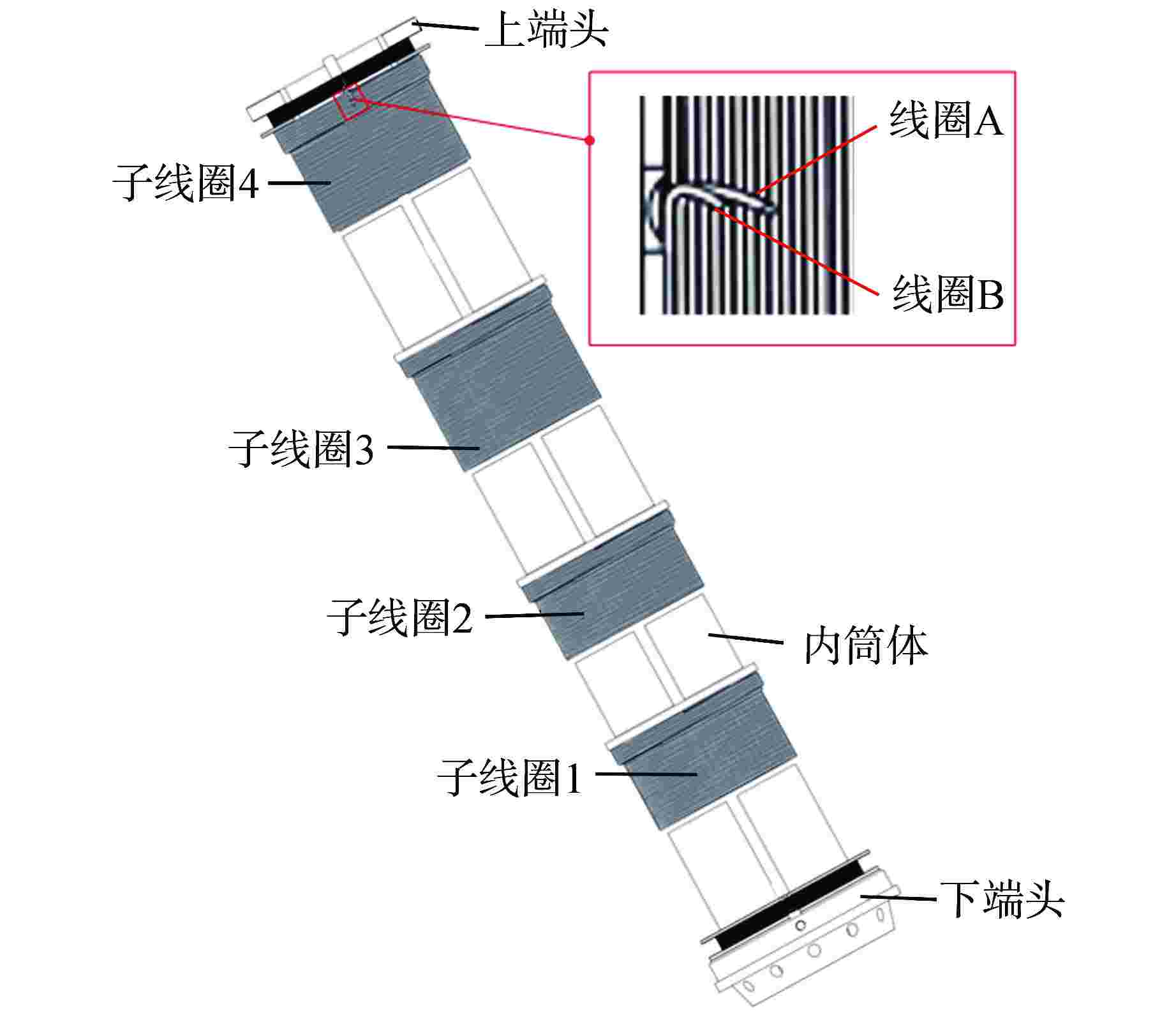
摘要: 目前编码式棒位探测器存在线圈数量多、结构复杂、测量精度粗略、可靠性差等诸多问题，严重阻碍了反应堆小型化的发展。本文提出一种新型自感式棒位探测器，采用四段等长度、A与B组线圈双匝并绕的探测结构，其中两组线圈相互独立，利用线圈电感随驱动杆移动的线性变化来实现连续棒位测量。通过量化驱动杆上的磁趋肤效应，推导基于涡流效应的自感式棒位探测器数学模型；搭建有限元仿真模型验证数学模型的准确性，研究驱动杆温升、探测线圈关键结构参数对探测器测量精度的影响，发现不同温升下线圈电感变化由驱动杆相对磁导率和电导率共同作用，线圈匝数增加有利于提高线圈电感变化量，线圈间距增加使线圈电感灵敏度先增加后减小，结合上述规律优化探测器结构；制造样机完成试验验证，结果表明两组线圈均具有0.14 mH/10 mm的电感分辨率，可实现10 mm的位移辨识精度。本研究可以为自感式棒位探测器在小型核反应堆中的应用提供参考。
- 反应堆 /
- 棒位探测器 /
- 涡流效应 /
- 电感解析计算
Abstract: Currently, coded rod position detectors have many problems such as a large number of coils, complex structure, rough measurement accuracy and poor reliability, which seriously hinder the development of reactor miniaturization. Therefore, we propose a new self-sensing rod position detector in this paper, which employs a double-winding structure with four equal-length A and B coils, where the two sets of coils are independent of each other, and the linear variation of the coil inductance with the motion of the driving rod enables continuous rod position measurement. By quantifying the magnetic skin effect on the rod, the mathematical model of self-sensing rod position detector based on eddy current effect is derived. The finite element simulation model is built to verify the accuracy of the mathematical model, and the influence of the temperature rise of the rod and the key structure parameters of the detection coil on the measurement accuracy of the detector is studied. It is found that the inductance variation of the coil under different temperatures is influenced by the relative permeability and conductivity of the rod. The increase of coil turns is conducive to the increase of inductance variation, and the increase of coil spacing first increases and then decreases the inductance sensitivity. And then the detector structure is optimized considering the above change rules. The prototype is tested and verified. The results show that both coils have an inductance resolution of 0.14 mH/10 mm, and the displacement identification accuracy of 10 mm can be achieved. This study can provide reference for the application of self-sensing rod position detectors in small nuclear reactors.
- Reactor /
- Rod position detector /
- Eddy current effect /
- Inductance analytical calculation

HTML全文

图 1 自感式棒位探测器结构

Figure 1. Self-Sensing Rod Position Detector Structure

下载: 全尺寸图片幻灯片

图 2 探测线圈结构示意图

Figure 2. Detector Coil Structure

下载: 全尺寸图片幻灯片

图 3 棒位探测器结构示意图

l_c—驱动杆进入线圈的长度，R_go—驱动杆半径

Figure 3. Rod Position Detector Structure

下载: 全尺寸图片幻灯片

图 4 探测器二维轴对称仿真模型

Figure 4. Two-Dimensional Axisymmetric Simulation Model of the Detector

下载: 全尺寸图片幻灯片

图 5 空心探测线圈磁场仿真结果与计算结果对比

Figure 5. Comparison between Simulation Results and Calculation Results of Hollow Detector Coil Magnetic Field

下载: 全尺寸图片幻灯片

图 6 线圈仿真电感与计算电感对比

Figure 6. Comparison of Coil Simulation Inductance and Calculated Inductance

下载: 全尺寸图片幻灯片

图 7 不同温度下驱动杆相对磁导率和电导率

Figure 7. Relative Permeability and Conductivity of Drive Rod at Different Temperatures

下载: 全尺寸图片幻灯片

图 8 不同温度下线圈电感变化

Figure 8. Coil Inductance at Different Temperatures

下载: 全尺寸图片幻灯片

图 9 导体线径对线圈电感的影响

Figure 9. Influence of Conductor Diameter on Coil Inductance

下载: 全尺寸图片幻灯片

图 10 线圈层数对线圈电感的影响

Figure 10. Influence of the Number of Coil Layers on Coil Inductance

下载: 全尺寸图片幻灯片

图 11 线圈间距对线圈电感的影响

Figure 11. Influence of Coil Spacing on Coil Inductance

下载: 全尺寸图片幻灯片

图 12 线圈间距对A2子线圈电感灵敏度的影响

Figure 12. Influence of Coil Spacing on A2 Subcoil Inductance Sensitivity

下载: 全尺寸图片幻灯片

图 13 试验样机测试平台示意图

Figure 13. Schematic Diagram of Experimental Prototype Test Platform

下载: 全尺寸图片幻灯片

图 14 试验样机A组线圈电感测试结果

Figure 14. Measured Results of Coil Inductance of Group A

下载: 全尺寸图片幻灯片

图 15 试验样机B组线圈电感测试结果

Figure 15. Measured Results of Coil Inductance of Group B

下载: 全尺寸图片幻灯片

表 1 棒位探测器初始参数

Table 1. Initial Parameters of Rod Position Detector

参数名	参数值
探测线圈总长/mm	1995
线圈分段/段	4
线圈内径/mm	119
单段线圈长度/mm	495
导体线径/mm	2
单段A(B)组线圈总匝数/匝	124×2
线圈层数/层	2
相邻线圈间隔/mm	5
驱动杆半径/mm	22.25
驱动杆长度/mm	2500
线圈间距/mm	3
激励电流幅值/A	0.1
激励电流频率/Hz	200

下载: 导出CSV

表 2 探测线圈优化参数

Table 2. Detector Coil Optimization Parameters

参数名	参数值
导体线径/mm	1.40
单段A(B)组线圈总匝数/匝	180×3
线圈层数/层	3
线圈间距/mm	5

下载: 导出CSV

表 3 探测线圈电感灵敏度

Table 3. Inductance Sensitivity of Detector Coil

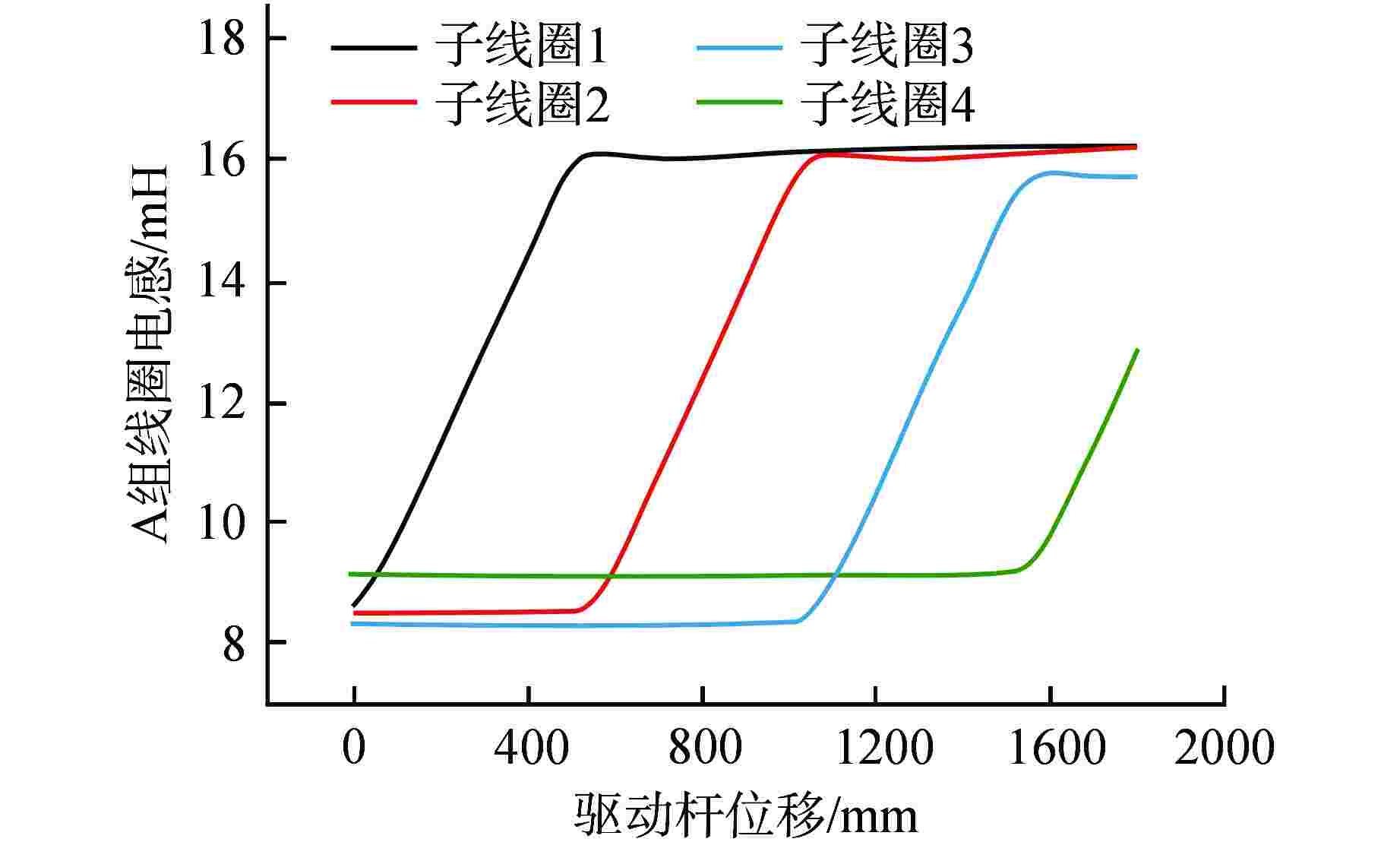
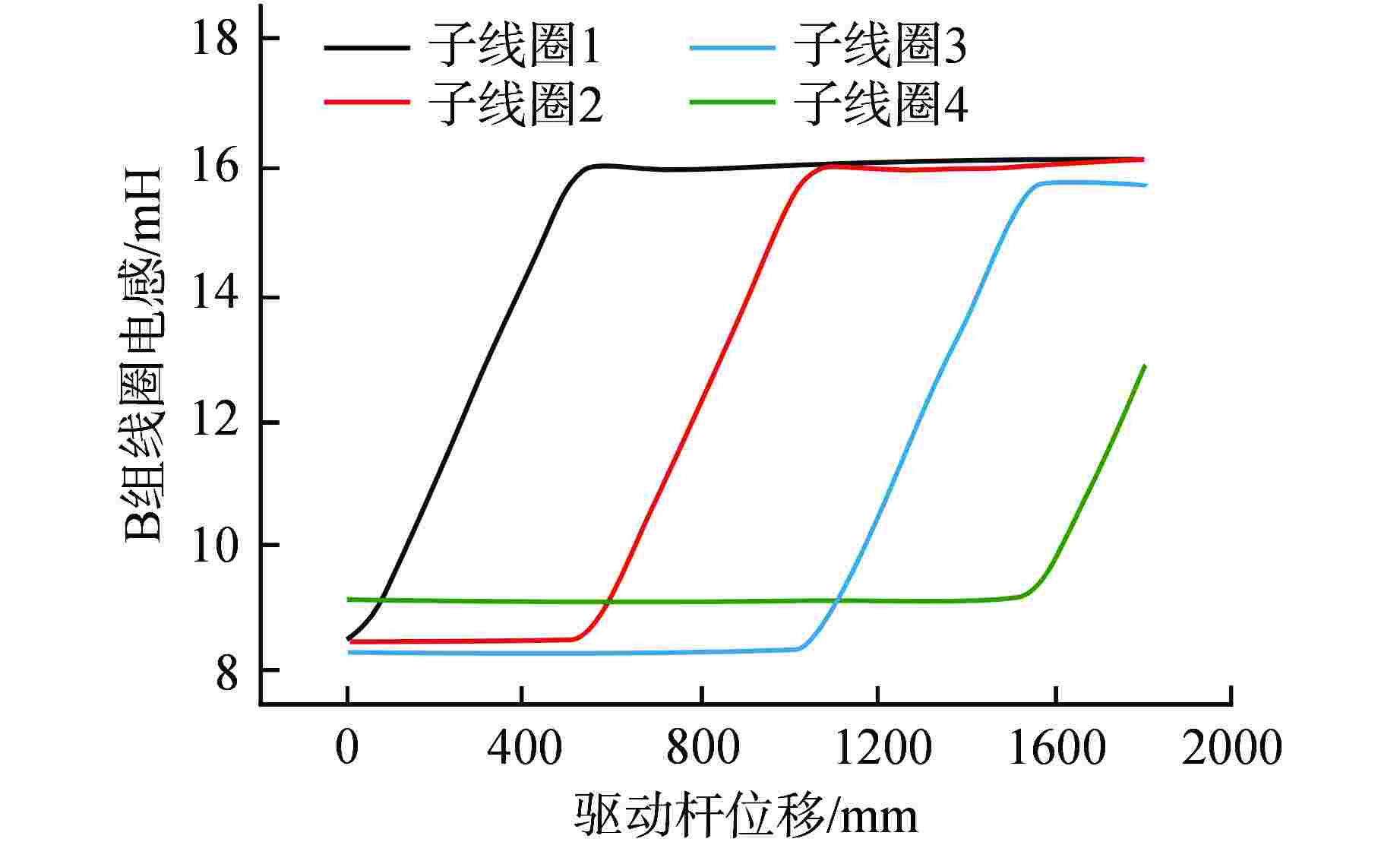
子线圈序号	A组线圈电感灵敏度/ [mH·(10 mm⁻¹)]	B组线圈电感灵敏度/ [mH·(10 mm⁻¹)]
1	0.145	0.143
2	0.139	0.139
3	0.136	0.137
4	0.132	0.132

下载: 导出CSV

参考文献(11)

[1]	李彦霖,秦本科,薄涵亮. 电容式棒位测量传感器的解析模型及验证[J]. 清华大学学报: 自然科学版,2022, 62(10): 1636-1644.
[2]	胡广,薄涵亮. 控制棒棒位测量系统中两极板电容传感器设计[J]. 原子能科学技术,2017, 51(12): 2352-2356.
[3]	李涛,张晋宝. 棒位探测器辅助线圈开路补偿设计[J]. 核电子学与探测技术,2021, 41(2): 338-343.
[4]	李梦书,李国勇,郑杲,等. 基于前馈控制的棒位探测器励磁电源研究与设计[J]. 核动力工程,2021, 42(1): 177-181.
[5]	杨文清,柳继坤,黄楚浩,等. 某核电厂控制棒测量棒位跳变问题分析与处理[J]. 核动力工程,2021, 42(6): 215-218.
[6]	LEE J S, CHO S S, KIM J W. Study on rod position indication system using permanent magnets with shielding plates for a control rod drive mechanism[J]. Journal of Magnetics, 2015, 20(4): 439-443. doi: 10.4283/JMAG.2015.20.4.439
[7]	PARK Y B, KIM J W, LEE J S. Study on magnetic property for test coil and permanent magnet[J]. Journal of the Korean Magnetics Society, 2016, 26(5): 154-158. doi: 10.4283/JKMS.2016.26.5.154
[8]	陈梅,田树龙. 控制棒位置指示系统数字化设计[J]. 核电子学与探测技术,2017, 37(1): 108-112.
[9]	于天达,吴昊,陈西南,等. 核反应堆控制棒驱动机构用棒位探测器及其使用方法: 中国,112071456A[P]. 2020-12-11.
[10]	BÖCKER J. Analysis of the magnetic skin effekt in motors and inductors[C]//International Symposium on Power Electronics, Electrical Drives, Automation and Motion. Sorrento, Italy: IEEE, 2020: 103-107.
[11]	SIM J H, KIM D Y, KIM S I, et al. Analytical electromagnetic modeling and experimental validation of vehicle horn considering skin effect in its solid cores[J]. IEEE Transactions on Magnetics, 2017, 53(6): 8001704.