考虑微动磨损下蒸汽发生器传热管时变可靠性评估方法

薛颖成; 吴宗辉; 何建

doi:10.13832/j.jnpe.2024.01.0164

考虑微动磨损下蒸汽发生器传热管时变可靠性评估方法

doi: 10.13832/j.jnpe.2024.01.0164

哈尔滨工程大学航天与建筑工程学院，哈尔滨，150001

基金项目: 国家自然科学基金面上项目（52278297）

详细信息

作者简介:
薛颖成（1997—），男，硕士研究生，现主要从事反应堆一回路可靠性研究，E-mail: 2016020321@hrbeu.edu.cn

通讯作者:
何　建，E-mail: hejian@hrbeu.edu.cn

中图分类号: TL353.13
计量
- 文章访问数: 111
- HTML全文浏览量: 32
- PDF下载量: 29
- 被引次数: 0
出版历程
- 收稿日期: 2023-03-05
- 修回日期: 2023-09-20
- 刊出日期: 2024-02-15

Time-varying Reliability Evaluation Method of Steam Generator Heat Transfer Tubes Considering Fretting Wear

School of Aerospace and Architectural Engineering, Harbin Engineering University, Harbin, 150001, China

摘要

摘要: 为了探究微动磨损对冲击作用下蒸汽发生器传热管可靠性的影响，建立了一种蒸汽发生器传热管安全性能的评估方法。通过拟合传热管磨损系数的分布形式，建立了传热管的磨损时变模型；运用乘子降维法获得传热管极限状态分数阶矩，使用NM（Nelder-Mead）单纯形算法优化最大熵参数来计算传热管的失效概率；基于时间离散法，对冲击作用下蒸汽发生器传热管在微动磨损影响下的时变可靠性进行研究。结果表明，在以可靠性指标大于2作为结构可靠的接受标准时，在第10年磨损状态下，遭受冲击作用的蒸汽发生器传热管时变可靠性已不能满足要求。
- 时变可靠性 /
- 微动磨损 /
- 蒸汽发生器传热管 /
- 最大熵原理
Abstract: In order to investigate the impact of fretting wear on the reliability of steam generator heat transfer tubes under impact, an evaluation method for the safety performance of steam generator heat transfer tubes was established. By fitting the distribution form of the wear coefficient of the heat transfer tube, a time-varying wear model of the heat transfer tube was established. Using the multiplier dimensionality reduction method to obtain the fractional moment of the limit state of the heat transfer tube, and using the NM (Nelder Mead) simplex algorithm to optimize the maximum entropy parameter to calculate the failure probability of the heat transfer tube. Based on the time discrete method, the time-varying reliability of steam generator heat transfer tubes under impact and fretting wear is studied. The results indicate that when the reliability index greater than 2 is taken as the acceptable standard of structural reliability, the time-varying reliability of the steam generator heat transfer tubes subjected to impact cannot meet the requirements in the 10th year of wear.
- Time-varying reliability /
- Fretting wear /
- Steam generator heat transfer tube /
- Maximum entropy principle

HTML全文

图 1 时变可靠性评估方法流程图

Figure 1. Flow Chart of Time-varying Reliability Evaluation Method

下载: 全尺寸图片幻灯片

图 2 蒸汽发生器传热管有限元模型

Figure 2. Finite Element Model of Steam Generator Heat Transfer Tube

下载: 全尺寸图片幻灯片

图 3 正负三角波

Figure 3. Positive and Negative Triangular Wave

下载: 全尺寸图片幻灯片

图 4 各服役时间段极限状态概率密度曲线

Figure 4. Probability Density Curve of Limit State for Each Service Period

下载: 全尺寸图片幻灯片

图 5 失效概率年限变化曲线

Figure 5. Variation Curve of Failure Probability with Service Time　　　　　

下载: 全尺寸图片幻灯片

表 1 微动磨损数据

Table 1. Fretting Wear Data

样本序号	K/10⁻¹⁵ Pa⁻¹	样本序号	K/10⁻¹⁵ Pa⁻¹
1	150.00	11	150.00
2	164.29	12	175.00
3	80.00	13	345.24
4	188.24	14	157.45
5	195.00	15	286.00
6	145.00	16	111.11
7	52.00	17	242.37
8	264.00	18	231.34
9	196.30	19	205.33
10	332.35	20	194.05

下载: 导出CSV

表 2 传热管不确定参数分布特征

Table 2. Distribution Characteristics of Uncertain Parameters of Heat Transfer Tube

随机变量	分布类型	均值	变异系数
管道外径	Normal	19.05 mm	0.05
管壁厚度	Normal	1.09 mm	0.05
屈服强度	Normal	305 MPa	0.10
管道外压	Normal	6.89 MPa	0.05
管道内压	Normal	15.5 MPa	0.05

下载: 导出CSV

表 3 磨损深度与服役时间关系

Table 3. Relationship between Wear Depth and Service Time

时间/a	磨损深度/mm	磨损占比/%
2	0.17	15.60
4	0.27	24.77
6	0.35	32.11
8	0.43	39.45
10	0.49	44.95
12	0.56	51.38
14	0.62	56.88

下载: 导出CSV

表 4 蒸汽发生器传热管各服役时间段最大熵参数

Table 4. Maximum Entropy Parameters of Steam Generator Heat Transfer Tube at Each Service Time

服役时间/a	参数	i=0	i=1	i=2	i=3
0	$ {\lambda _i} $	707.7007	36.7743	698.8369	−1398.7299
0	$ {k_i} $		−1.4865	0.7809	0.4575
2	$ {\lambda _i} $	4.6292	2.4339	1429.2406	−1429.3749
2	$ {k_i} $		−16.4174	14.2140	14.2138
4	$ {\lambda _i} $	707.9341	324.2745	−1027.0436	1.5032
4	$ {k_i} $		0.1446	0.0802	4.1395
6	$ {\lambda _i} $	−307.4294	−224.8584	222.9042	310.4169
6	$ {k_i} $		2.8770	−1.1710	2.7012
8	$ {\lambda _i} $	6.4855	−763.2724	0.3480	757.7488
8	$ {k_i} $		13.9580	−1.1346	13.9998
10	$ {\lambda _i} $	0.7082	−1966.6420	1.1369	1964.7435
10	$ {k_i} $		20.7476	−5.5894	20.7548
12	$ {\lambda _i} $	80.0618	−3.2020	−79.9338	2.2598
12	$ {k_i} $		20.9962	0.1896	24.2862
14	$ {\lambda _i} $	−159.8093	−1.8743	159.5186	0.8963
14	$ {k_i} $	−	18.8962	−0.0750	26.6337

下载: 导出CSV

表 5 可靠性指标计算结果

Table 5. Calculation Results of Reliability Index

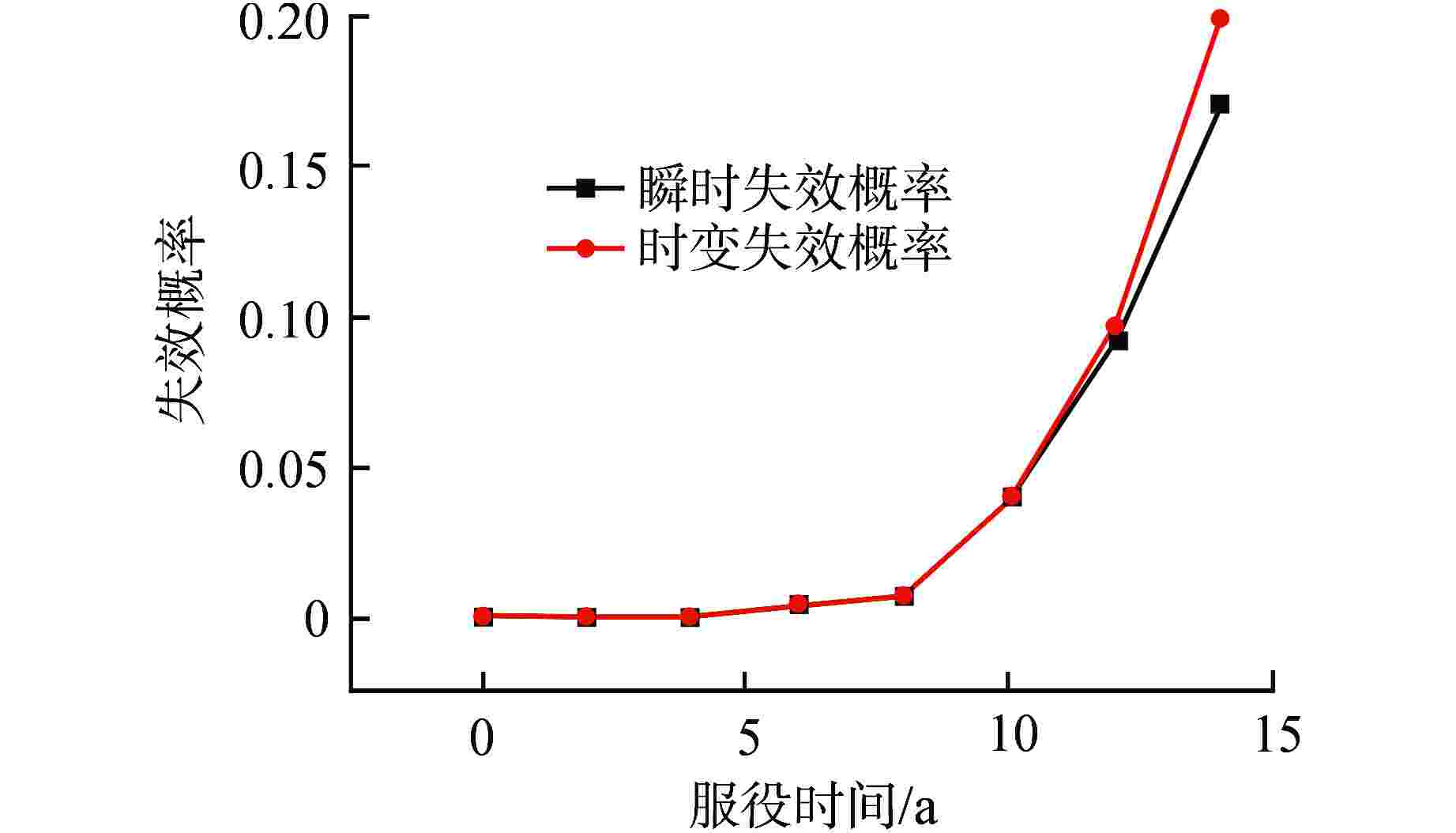
服役时间/a	瞬时失效概率	时变失效概率	时变可靠性指标
0	$ {\text{2}}{\text{.8737}} \times {\text{1}}{{\text{0}}^{ - 22}} $	$ {\text{2}}{\text{.8737}} \times {\text{1}}{{\text{0}}^{ - 22}} $	9.6340
2	$ {\text{1}}{\text{.7821}} \times {\text{1}}{{\text{0}}^{ - 5}} $	$ {\text{1}}{\text{.7821}} \times {\text{1}}{{\text{0}}^{ - 5}} $	4.1341
4	$ {\text{4}}{\text{.1034}} \times {\text{1}}{{\text{0}}^{ - 5}} $	$ {\text{4}}{\text{.1035}} \times {\text{1}}{{\text{0}}^{ - 5}} $	3.9383
6	$ {\text{4}}{\text{.5241}} \times {\text{1}}{{\text{0}}^{ - 3}} $	$ {\text{4}}{\text{.5243}} \times {\text{1}}{{\text{0}}^{ - 3}} $	2.6102
8	$ {\text{7}}{\text{.1698}} \times {\text{1}}{{\text{0}}^{ - 3}} $	$ {\text{7}}{\text{.2029}} \times {\text{1}}{{\text{0}}^{ - 3}} $	2.4470
10	$ {\text{4}}{\text{.0114}} \times {\text{1}}{{\text{0}}^{ - 2}} $	$ {\text{4}}{\text{.0589}} \times {\text{1}}{{\text{0}}^{ - 2}} $	1.7439
12	$ {\text{9}}{\text{.3039}} \times {\text{1}}{{\text{0}}^{ - 2}} $	$ {\text{9}}{\text{.8076}} \times {\text{1}}{{\text{0}}^{ - 2}} $	1.2926
14	$ {\text{1}}{\text{.7185}} \times {\text{1}}{{\text{0}}^{ - 1}} $	$ {\text{1}}{\text{.9974}} \times {\text{1}}{{\text{0}}^{ - 1}} $	0.8426

下载: 导出CSV

参考文献(15)

[1]	臧希年. 核电厂系统及设备[M]. 北京:清华大学出版社,2010: 65-66.
[2]	SORIA S R, CLARAMONTE S, YAWNY A. Evolution of fretting wear with the number of cycles on Inconel 690 steam generator tubes against AISI 420 steel under gross slip conditions[J]. Tribology International, 2021, 155: 106803. doi: 10.1016/j.triboint.2020.106803
[3]	YANG S, CAI Z B, CHEN Z Q, et al. Impact fretting wear of Inconel 690 tube with different supporting structure under cycling low kinetic energy[J]. Wear, 2017, 376-377: 625-633. doi: 10.1016/j.wear.2017.01.011
[4]	RYU K W, PARK C Y, KIM H N, et al. Prediction of fretting wear depth for steam generator tubes based on various types of wear scars[J]. Journal of Nuclear Science and Technology, 2010, 47(5): 449-456. doi: 10.1080/18811248.2010.9711635
[5]	ANG A H S, CORNELL C A. Reliability bases of structural safety and design[J]. Journal of the Structural Division, 1974, 100(9): 1755-1769. doi: 10.1061/JSDEAG.0003870
[6]	RUBINSTEIN R Y, KROESE D P. Simulation and the Monte Carlo method[M]. Hoboken: John Wiley & Sons, 2008: 49-90.
[7]	ZHANG X F, PANDEY M D. Structural reliability analysis based on the concepts of entropy, fractional moment and dimensional reduction method[J]. Structural Safety, 2013, 43: 28-40. doi: 10.1016/j.strusafe.2013.03.001
[8]	KULLBACK S, LEIBLER R A. On information and sufficiency[J]. Annals of Mathematical Statistics, 1951, 22(1):79-86. KULLBACK S, LEIBLER R A. On information and sufficiency[J]. Annals of Mathematical Statistics, 1951, 22(1):79-86.
[9]	LAGARIAS J C, REEDS J A, WRIGHT M H, et al. Convergence properties of the nelder--mead simplex method in low dimensions[J]. SIAM Journal on Optimization, 1998, 9(1): 112-147.
[10]	洪华生, 邓汉忠. 工程中的概率概念: 在土木与环境工程中的应用[M]. 陈建兵, 彭勇波,刘威, 等, 译. 北京:中国建筑工业出版社, 2017: 37-55. 洪华生, 邓汉忠. 工程中的概率概念: 在土木与环境工程中的应用[M]. 陈建兵, 彭勇波, 刘威, 等, 译. 北京: 中国建筑工业出版社, 2017: 37-55.
[11]	ARCHARD J F. Contact and rubbing of flat surfaces[J]. Journal of Applied Physics, 1953, 24(8): 981-988. doi: 10.1063/1.1721448
[12]	KIM D G, LEE Y Z. Experimental investigation on sliding and fretting wear of steam generator tube materials[J]. Wear, 2001, 250(1-12): 673-680. doi: 10.1016/S0043-1648(01)00676-7
[13]	谷耀新. 三参数威布尔分布参数估计方法[J]. 沈阳工业学院学报,1997,16(4):53-57.
[14]	LOPES R H C. Kolmogorov–Smirnov test[M]//LOVRIC M. International Encyclopedia of Statistical Science. Berlin, Heidelberg: Springer, 2014: 718-720.
[15]	刘文思, 王鑫. 舰船水密门设备抗冲击性能对比研究[J]. 舰船电子工程, 2020, 40(1):5. 刘文思, 王鑫. 舰船水密门设备抗冲击性能对比研究[J]. 舰船电子工程, 2020, 40(1):5.