松散耦合系统蒙特卡罗临界计算源收敛判定方法研究

张寅; 成昱廷; 周琦; 朱庆福; 夏兆东; 宁通; 张振洋

doi:10.13832/j.jnpe.2024.02.0010

松散耦合系统蒙特卡罗临界计算源收敛判定方法研究

doi: 10.13832/j.jnpe.2024.02.0010

张寅^1,,
成昱廷^2, ,,
周琦²,
朱庆福²,
夏兆东²,
宁通²,
张振洋²

1.
国家国防科技工业局核技术支持中心，北京，100070
2.
中国原子能科学研究院反应堆工程技术研究所，北京，102413

详细信息

作者简介:
张　寅（1984—），男，高级工程师，现主要从事反应堆物理方向研究，E-mail: 1234mike1234@sina.com

通讯作者:
成昱廷，E-mail: chengyuting@ciae.ac.cn

中图分类号: TL329
计量
- 文章访问数: 161
- HTML全文浏览量: 37
- PDF下载量: 59
- 被引次数: 0
出版历程
- 收稿日期: 2023-07-03
- 修回日期: 2023-08-17
- 刊出日期: 2024-04-12

Research on the Source Convergence Diagnose Method of Monte Carlo Critical Calculation for Loosely Coupled System

1.
State Administration of Science, Technology and Industry for National Defence, Beijing, 100070, China
2.
Reactor Engineering Technology Research Institute, China Institute of Atomic Energy, Beijing, 102413, China

摘要

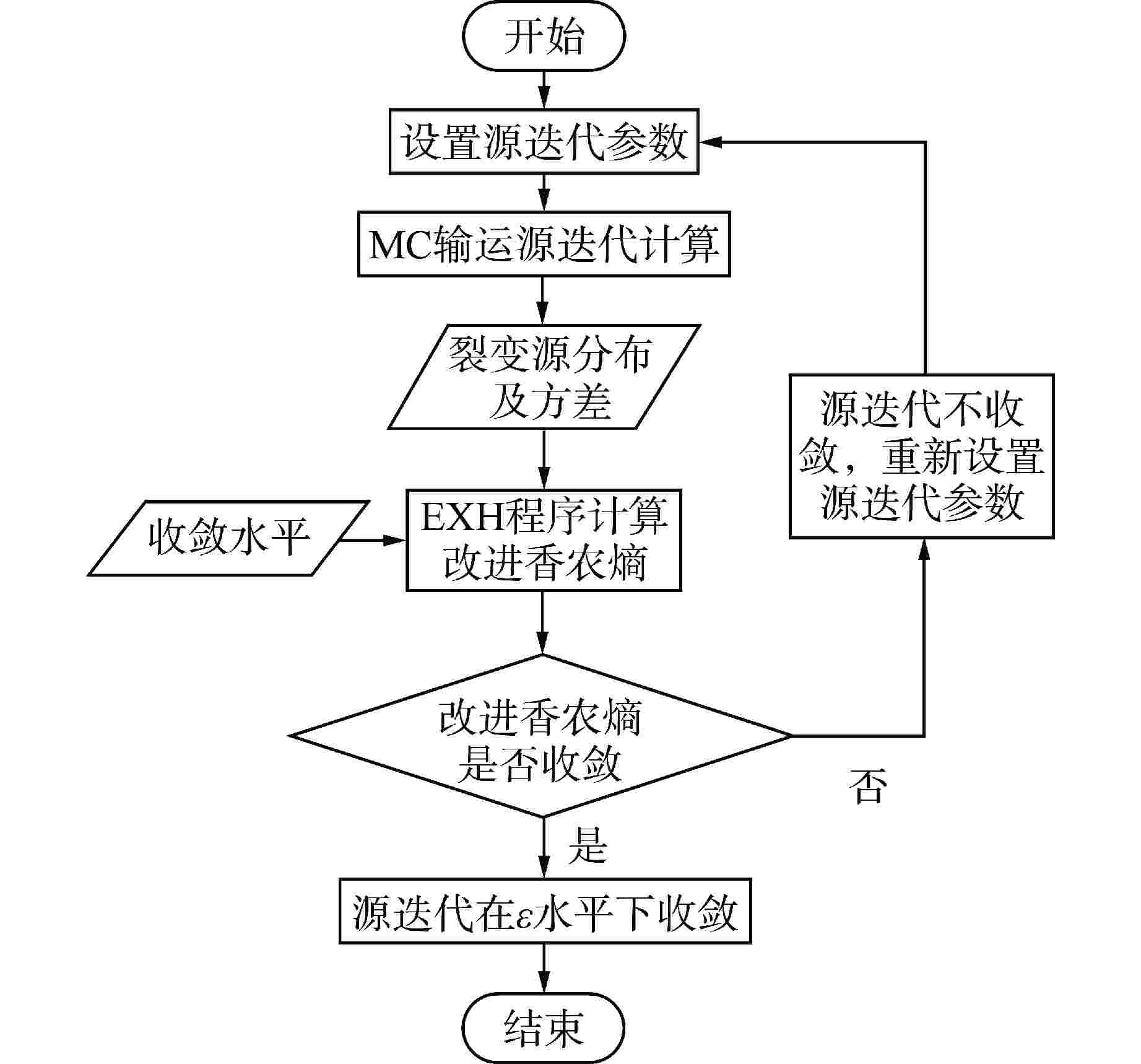
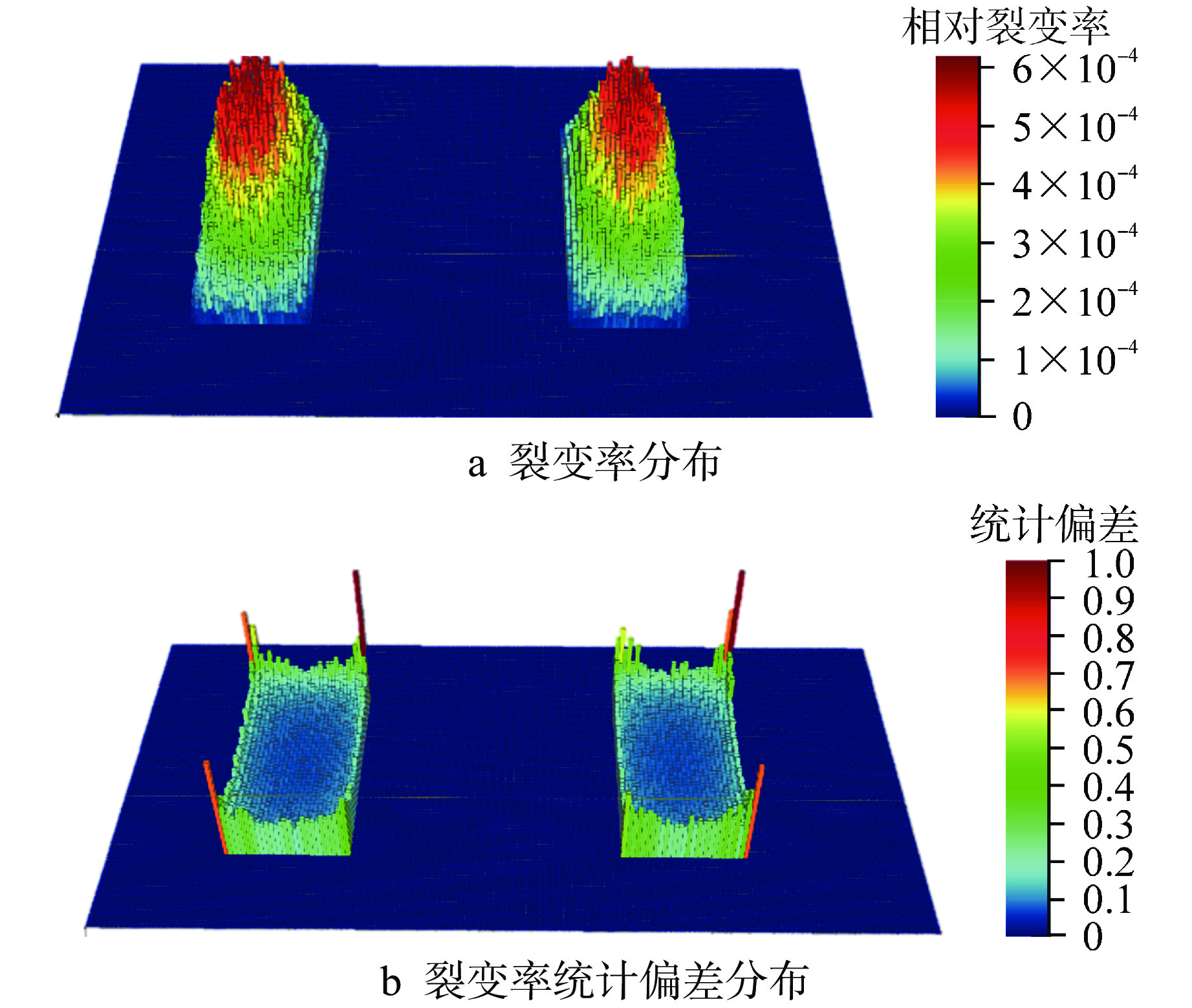
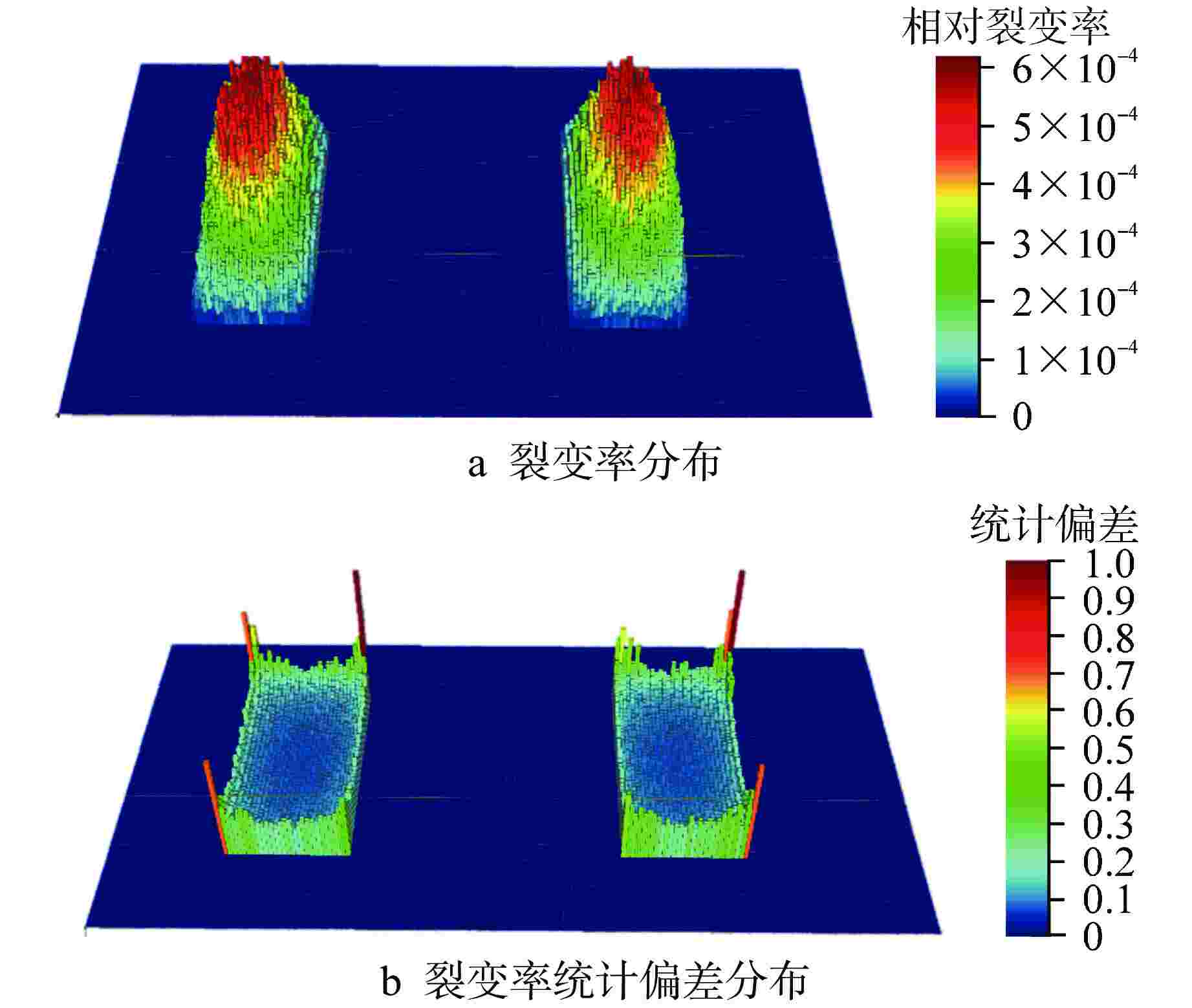
摘要: 为提高蒙特卡罗程序在松散耦合系统临界安全计算中的可靠性与准确性，需要对计算结果进行源收敛判定。本文提出了一种考虑裂变源分布及统计偏差权重因子的改进型香农熵的收敛判定方法，将裂变源迭代过程中相邻代际之间裂变源分布的相对偏差、源迭代过程中裂变源分布的蒙特卡罗统计标准差作为裂变源分布的权重，建立了改进型的香农熵收敛指标，弥补了传统香农熵对于局部裂变源收敛细节考虑的不足。将改进型的香农熵收敛指标应用在经合组织核能机构发布的乏燃料棒栅元和松散耦合铀溶液平板基准问题上。结果表明，对比传统香农熵源收敛判定指标，改进型的香农熵对裂变源迭代收敛过程更为敏感，能够更加直观和准确地判定裂变源分布伴随源迭代的收敛性。对于收敛速度慢的典型算例，应用传统香农熵判定收敛性时给出了伪收敛的结论，而改进型香农熵能准确地判定源迭代达到收敛时的迭代次数。
- 临界安全 /
- 蒙特卡罗 /
- 松散耦合系统 /
- 源收敛判定 /
- 香农熵
Abstract: In order to improve the reliability and accuracy of Monte Carlo code in the critical safety calculation of loosely coupled systems, it is necessary to determine the source convergence of the results. In this paper, an improved Shannon entropy diagnose method considering the distribution of fission sources and the statistical deviation weight factor is proposed. The relative deviation of fission sources distribution between adjacent generations and the standard deviation of fission source distribution during source iteration are used as the weight of fission source distribution. Finally, an improved Shannon entropy convergence index is established, which makes up for the shortcomings of traditional Shannon entropy for lacking the details of local fission source. The improved Shannon entropy convergence index is applied to the benchmark problem: spent fuel rod and loosely coupled solution slabs published by OECD/NEA. The results show that compared with the traditional Shannon entropy index, the improved Shannon entropy is more sensitive to the iterative convergence process of fission source, and can more intuitively and accurately determine the convergence of fission source distribution accompanied by source iteration. For a typical case with slow convergence speed, the conclusion of pseudo-convergence is given with the traditional Shannon entropy. The improved Shannon entropy can accurately determine the number of iterations when the source iteration reaches convergence.
- Critical safety /
- Monte Carlo /
- Loosely-coupled system /
- Source convergence diagnose /
- Shannon entropy

HTML全文

图 1 松散耦合系统裂变率及其统计偏差分布示意图

Figure 1. Fission Rate and Its Statistical Deviation Distribution of Loosely Coupled System

下载: 全尺寸图片幻灯片

图 2 改进香农熵源收敛判定流程

Figure 2. Improved Shannon Entropy Source Convergence Diagnose Process

下载: 全尺寸图片幻灯片

图 3 乏燃料元件单栅元模型

Figure 3. Single Cell Model of Spent Fuel Element

下载: 全尺寸图片幻灯片

图 4 不同初始裂变源对应的k_eff结果

Figure 4. k_eff Results Corresponding to Different Initial Fission Sources

下载: 全尺寸图片幻灯片

图 5 源迭代收敛判定指标

Figure 5. Source Iterative Convergence Diagnose Index

下载: 全尺寸图片幻灯片

图 6 松散耦合铀溶液平板问题

Figure 6. Loosely Coupled Uranyl Solution Slabs Problem

下载: 全尺寸图片幻灯片

图 7 松散耦合铀溶液平板源收敛计算结果

Figure 7. Source Convergence Results of Loosely Coupled Uranyl Solution Slabs

下载: 全尺寸图片幻灯片

表 1 乏燃料棒对称分布算例k_eff计算结果

Table 1. k_eff Calculation Results for Symmetrical Distribution of Spent Fuel Rods

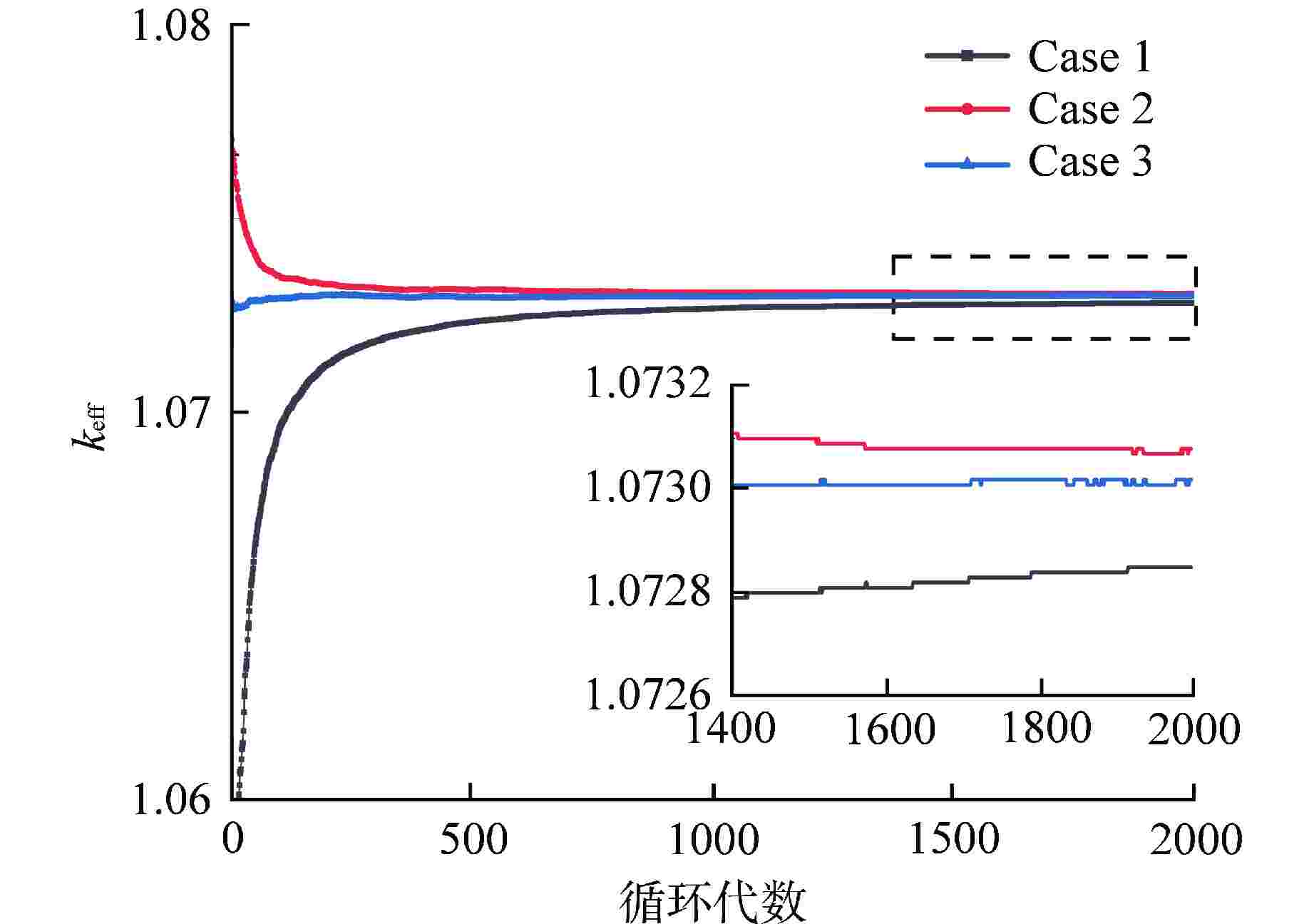
算例	k_eff	标准差	99%置信区间
Case 1	1.07285	0.00003	1.07276 ~ 1.07394
Case 2	1.07308	0.00002	1.07302 ~1.07314
Case 3	1.07302	0.00001	1.07299 ~1.07305

下载: 导出CSV

表 2 乏燃料棒对称分布算例k_eff计算时间

Table 2. k_eff Calculation Time for Symmetrical Distribution of Spent Fuel Rods

算例	标准计算时间/min	改进方法输运耗时/min	改进方法计算耗时/s	改进方法相对引入的额外计算成本/%
Case 1	265.11	276.23	1.480	4.15
Case 2	271.46	282.74	1.480	4.05
Case 3	263.22	274.65	1.480	4.18

下载: 导出CSV

表 3 松散耦合铀溶液平板问题计算案例

Table 3. Cases of Loosely Coupled Uranyl Solution Slabs Problem

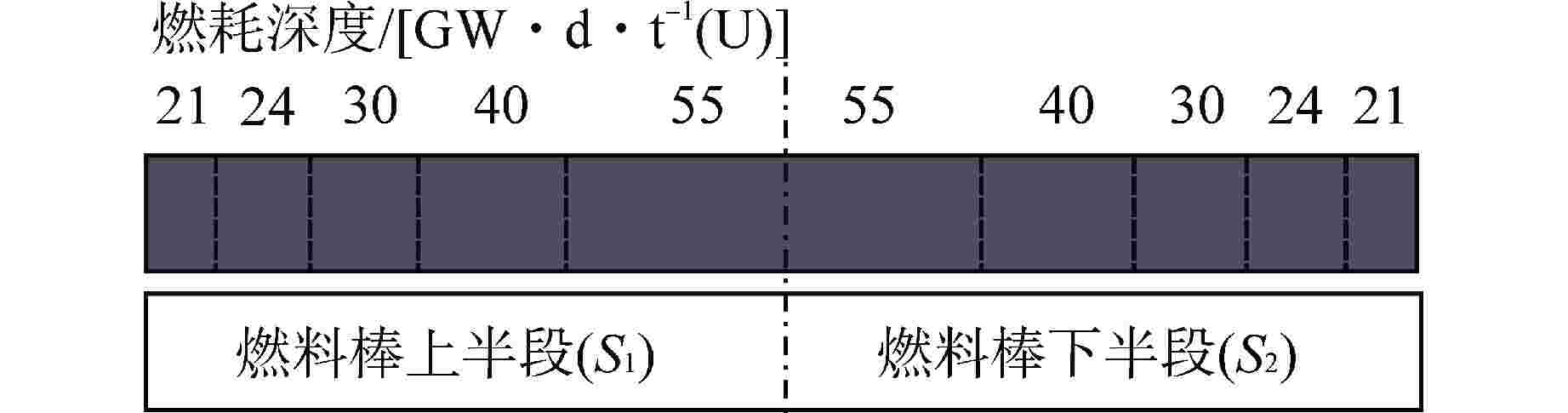
算例	水层厚度/cm	初始裂变源分布
Case 1	30	均匀分布
Case 2	20	均匀分布
Case 3	10	均匀分布

下载: 导出CSV

表 4 松散耦合铀溶液平板算例k_eff计算时间

Table 4. k_eff Calculation Time for Loosely Coupled Uranyl Solution Slabs

算例	标准计算时间/min	改进方法输运耗时/min	改进方法计算耗时/s	改进方法相对引入的额外计算成本/%
Case 1	69.31	71.43	0.760	3.06
Case 2	67.89	70.25	0.760	3.48
Case 3	66.74	68.97	0.760	3.34

下载: 导出CSV

参考文献(8)

[1]	吴晓飞,吴海成,刘振华,等. 蒙特卡罗方法计算特征值问题收敛性研究[J]. 中国原子能科学研究院年报,2006(1): 214.
[2]	NAITO Y, YANG J N. The sandwich method for determining source convergence in Monte Carlo calculation[J]. Journal of Nuclear Science and Technology, 2004, 41(5): 559-568. doi: 10.1080/18811248.2004.9715519
[3]	UEKI T, BROWN F B. Stationarity modeling and informatics-based diagnostics in Monte Carlo criticality calculations[J]. Nuclear Science and Engineering, 2005, 149(1): 38-50. doi: 10.13182/NSE04-15
[4]	WENNER M T, HAGHIGHAT A. A combined diagnostic approach for Monte Carlo source convergence identification, international conference on mathematics[C]//American Nuclear Society. International Conference on Advances in Mathematics, Computational Methods, and Reactor Physics. Saratoga: Springs, 2009.
[5]	X-5 Monte Carlo Team. MCNP – A general Monte Carlo n-particle transport code, Version 5, LA-UR-03-1987[R]. New mexico: Los Alamos National Laboratory, 2003.
[6]	OMAR M R. Numerical evidence on the formulation of the Fourier fundamental mode coefficient as a source convergence indicator[J]. Nuclear Engineering and Design, 2021, 378: 111162. doi: 10.1016/j.nucengdes.2021.111162
[7]	OMAR M R, KARIM J A. Fission source stationarity diagnostics using the Fourier fundamental mode coefficient[J]. Progress in Nuclear Energy, 2022, 146: 104164. doi: 10.1016/j.pnucene.2022.104164
[8]	BLOMQUIST R N, ARMISHAW M, HANLON D, et al. Source convergence in criticality safety analyses, Phase I: results for four test problems[Z]. OECD/NEA, 2006.