Research on Burnup Calculation Method Based on Splicing Fission Matrix
-
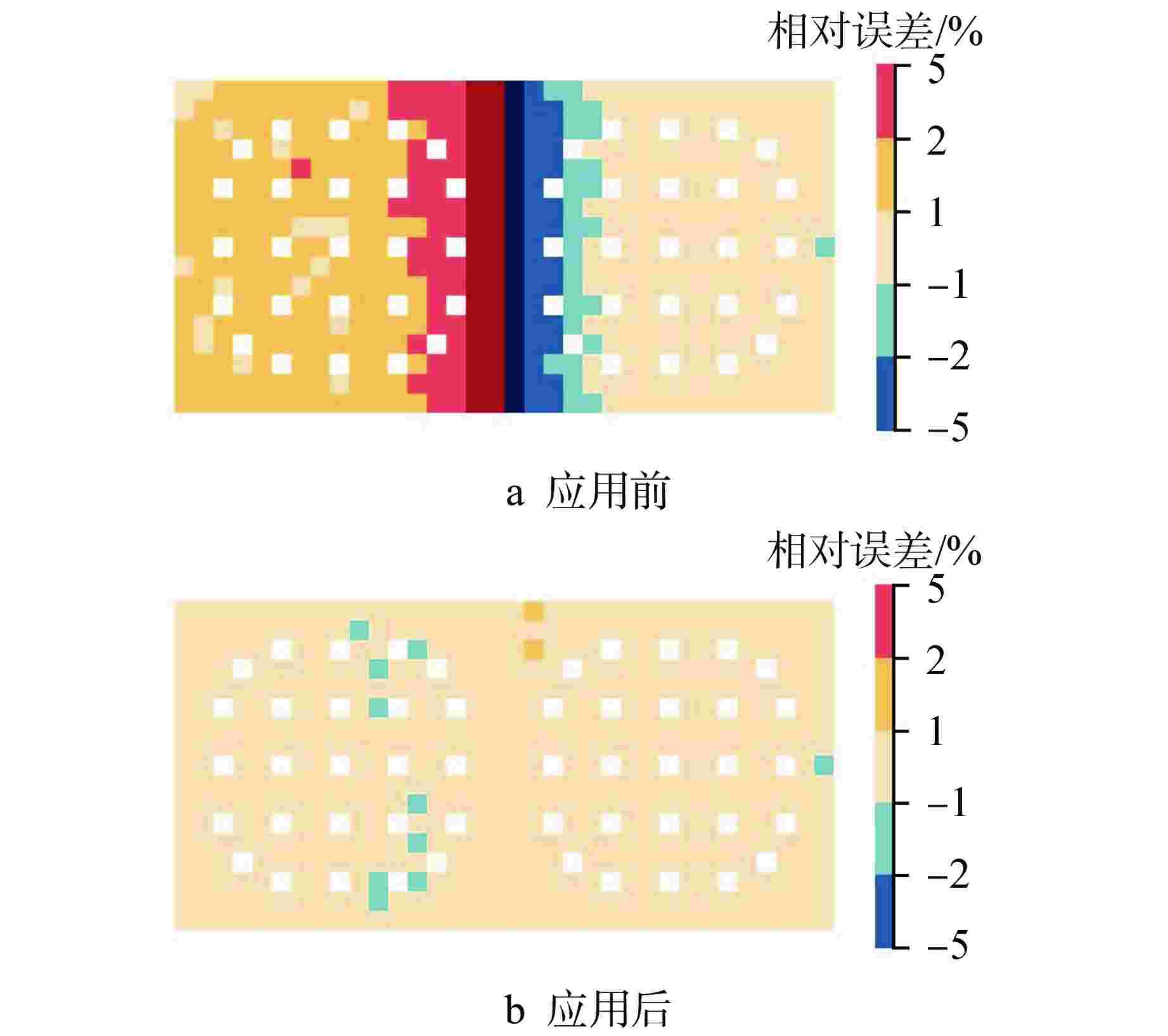
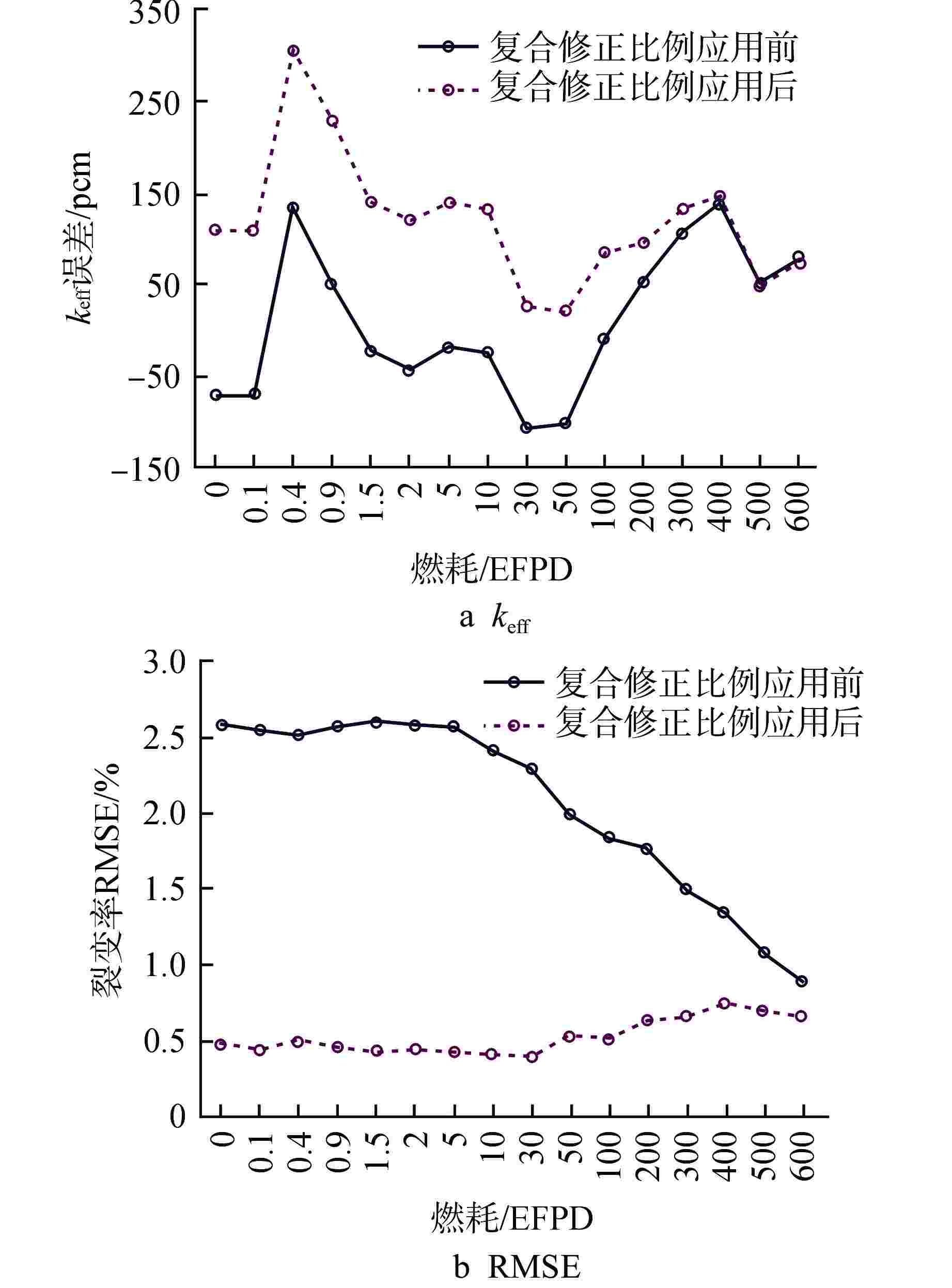
摘要: 为了实现高效率的输运-燃耗耦合计算，本文基于拼接裂变矩阵理论提出了一种新的燃耗计算方法。拼接裂变矩阵方法使系统的裂变矩阵可以通过预先计算的数据库获得，再根据计算模型的实际工况，按照终点区域性质进行拼接。裂变矩阵数据库采用蒙特卡罗固定源计算得到，堆芯计算也不需要蒙特卡洛模拟，因此可避开耗时的临界计算。本文采用新的燃耗计算方法计算了一个典型两组件模型燃耗600有效满功率天（EFPD）的有效增殖因子和裂变源分布，结果表明燃耗-富集度复合修正比例可将裂变源均方根误差控制在0.7%以下，证明该算法的可行性。Abstract: In order to realize efficient transport-burnup coupling calculation, a new calculation method based on splicing fission matrix theory is proposed in this paper. The combined fission matrix method enables to obtain the system fission matrix from a pre-calculated database, and then the database matrices are combined according to the actual conditions of the calculation model and the properties of the terminal area. The fission matrix database is obtained by Monte Carlo fixed source calculation, and the core calculation does not need Monte Carlo simulation, so the time-consuming critical calculation can be avoided. In this paper, the effective multiplication factor and fission source distribution of a typical two-assembly model with a burnup up to 600EFPD are obtained. The burnup-enrichment composite correction ratio can reduce the root-mean-square error of the fission source to less than 0.7%, thereby confirming the feasibility of this algorithm.
-
Key words:
- Splicing fission matrix /
- Monte Carlo /
- Burnup calculation
-
图 2 富集度修正比例应用前后裂变源分布相对误差
Figure 2. Relative Error of Fission Source Distribution before and after Application of Enrichment Correction Ratio
图 4 燃耗-富集度复合修正比例曲线
工况 1—左侧组件燃耗为55 MW·d·kg−1(U)； 工况 2—左侧组件燃耗为0平移至55 MW·d·kg−1(U)； 工况 3—左侧组件燃耗为6.5 MW·d·kg−1(U)； 工况 4—左侧组件燃耗为0平移至6.5 MW·d·kg−1(U)； 工况 5—左侧组件燃耗为0.65 MW·d·kg−1(U)； 工况6—左侧组件燃耗为0平移至0.65 MW·d·kg−1(U)； 工况7—左侧组件燃耗为0
Figure 4. Burnup-Enrichment Correction Ratio Curves
图 5 再修正因子h(i)随右侧燃耗深度的变化与3次多项式拟合
工况1—左侧组件燃耗为0平移至0.65 MW·d·kg−1(U)； 工况 2—工况1下3次多项式拟合； 工况 3—左侧组件燃耗为0 平移至6.5 MW·d·kg−1(U)； 工况 4—工况 3下3次多项式拟合； 工况 5—左侧组件燃耗为0 平移至55 MW·d·kg−1(U)； 工况 6—工况 5下3次多项式拟合
Figure 5. Re-correction Factor and Polynomial Fitting
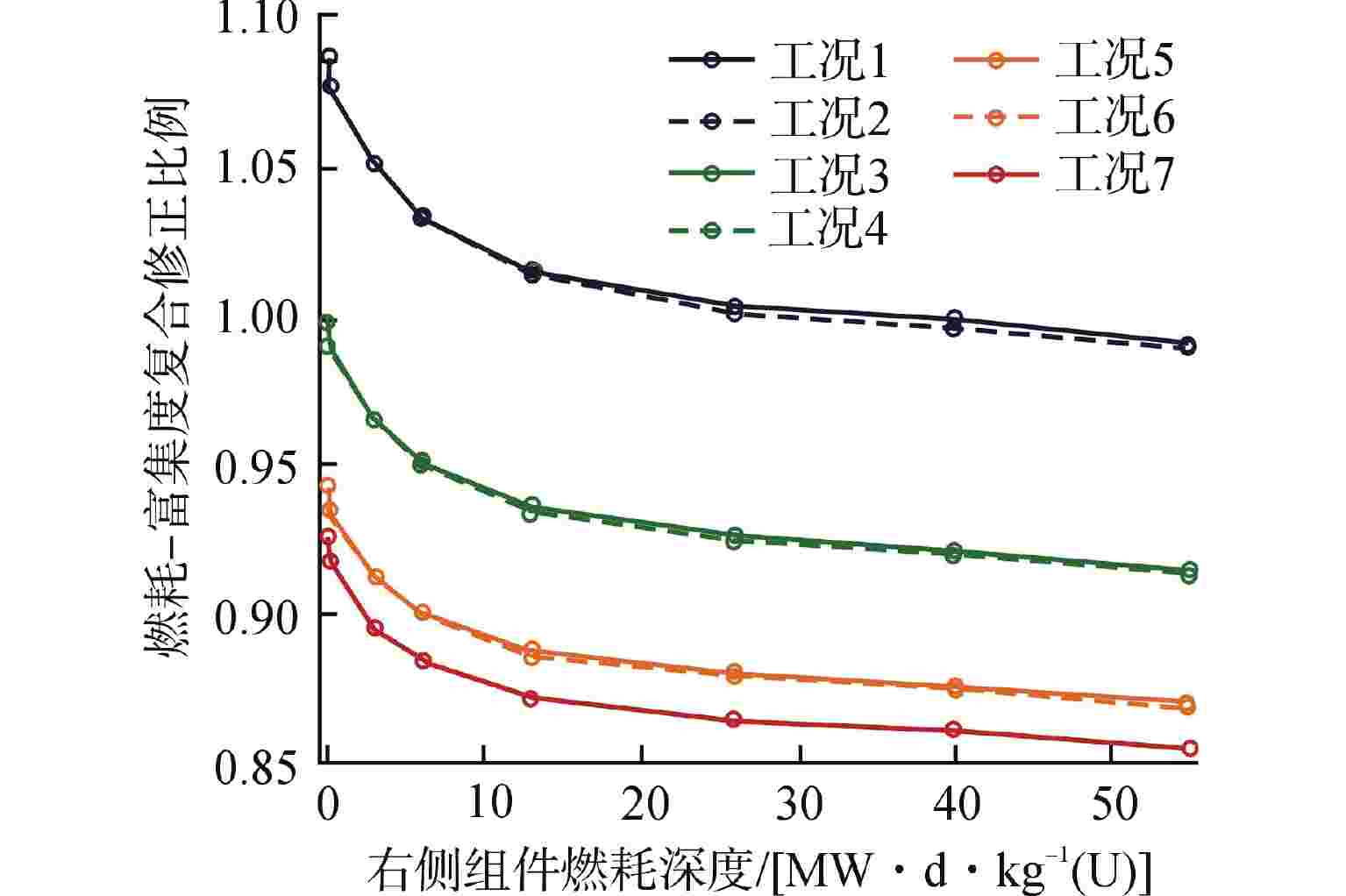
图 6 修正后的燃耗-富集度复合修正比例平移曲线
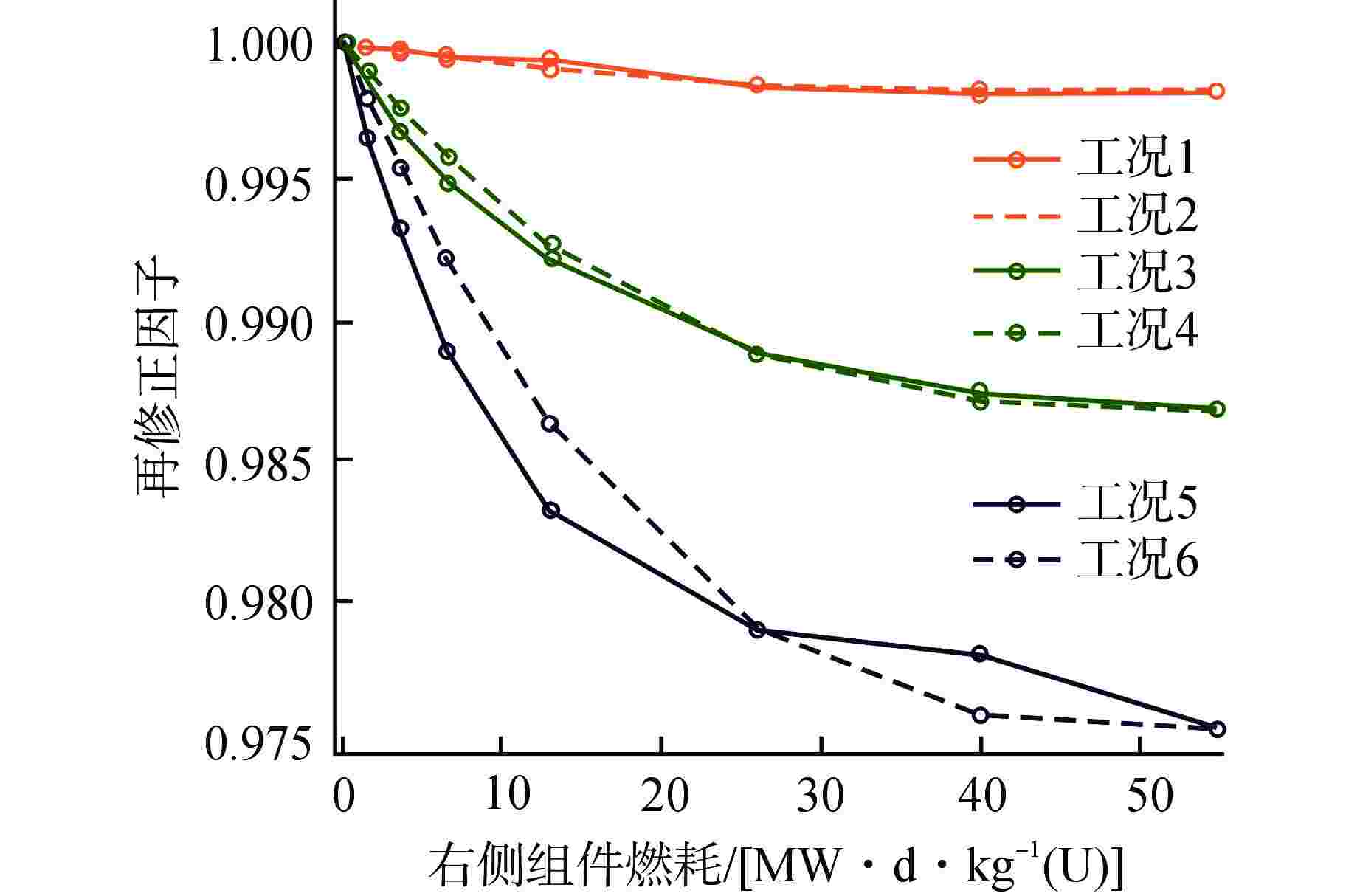
工况 1—左侧组件燃耗为55 MW·d·kg−1(U)；工况 2—左侧组件燃耗为55 MW·d·kg−1(U)平移再修正后；工况 3—左侧组件燃耗为6.5 MW·d·kg−1(U)；工况 4—左侧组件燃耗为6.5 MW·d·kg−1(U)平移再修正后；工况 5—左侧组件燃耗为0.65 MW·d·kg−1(U)；工况 6—左侧组件燃耗为0.65 MW·d·kg−1(U)平移再修正后；工况 7—左侧组件燃耗为0
Figure 6. Translation Curve for Corrected Burnup-Enrichment Composite Correction Ratio
图 7 两组件模型燃耗至600EFPD的keff误差和裂变率分布RMSE变化
EFPD—有效满功率天；1pcm=10−5
Figure 7. keff Error and RMSE Changes of Two-assembly Model with Burnup to 600EFPD
表 1 数据库中各步燃耗
Table 1. Burnups in the Database
步数 燃耗/[MW·d·kg−1(U)] 步数 燃耗/[MW·d·kg−1(U)] 1 5.00×10−3 8 1.50 2 1.50×10−2 9 3.50 3 5.00×10−2 10 6.50 4 0.10 11 13.00 5 0.15 12 26.00 6 0.35 13 40.00 7 0.65 14 55.00 
下载: 导出CSV
-
[1] WENNER M T, HAGHIGHAT A. A combined diagnostic approach for Monte Carlo source convergence identification[C]//Proceedings of the 2009 International Conference on Advances in Mathematics, Computational Methods, and Reactor Physics. New York: Saratoga Springs, 2009. [2] KAPLAN E L. Monte Carlo methods for equilibrium solutions in neutron multiplication: NSA-13-012787[M]. Livermore: University of California Lawrence Radiation Laboratory, 1958: 114-121. [3] CARNEY S, BROWN F, KIEDROWSKI B, et al. Theory and applications of the fission matrix method for continuous-energy Monte Carlo[J]. Annals of Nuclear Energy, 2014, 73: 423-431. doi: 10.1016/j.anucene.2014.07.020 [4] WALTERS W J, ROSKOFF N J, HAGHIGHAT A. The RAPID fission matrix approach to reactor core criticality calculations[J]. Nuclear Science and Engineering, 2018, 192(1): 21-39. doi: 10.1080/00295639.2018.1497395 -
计量
- 文章访问数: 107
- HTML全文浏览量: 26
- PDF下载量: 31
- 被引次数: 0
