Numerical Simulation Method of Boiling Heat Transfer and Its Application Characteristics under Multi-tube Coupled Heat Transfer
-
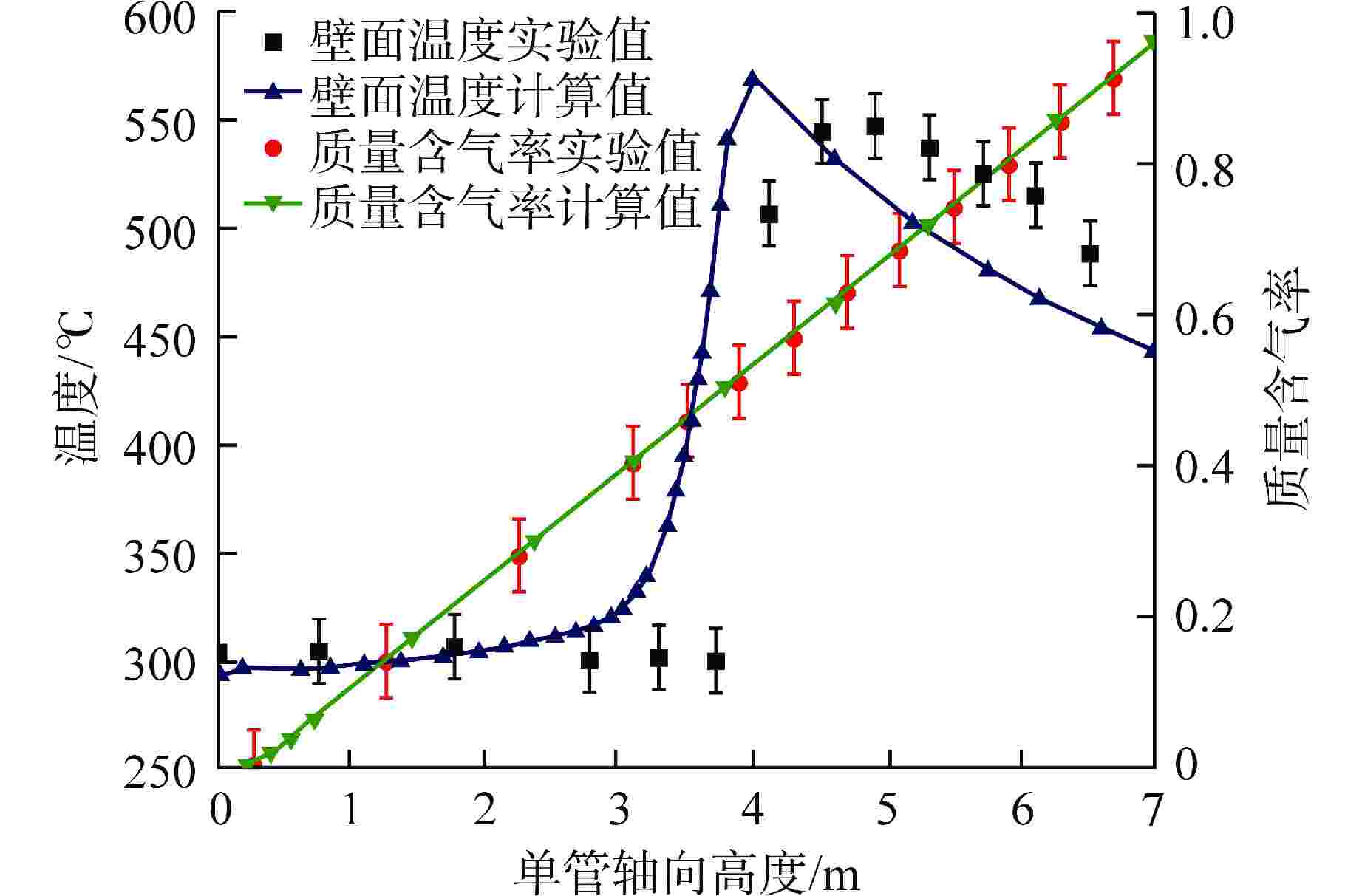
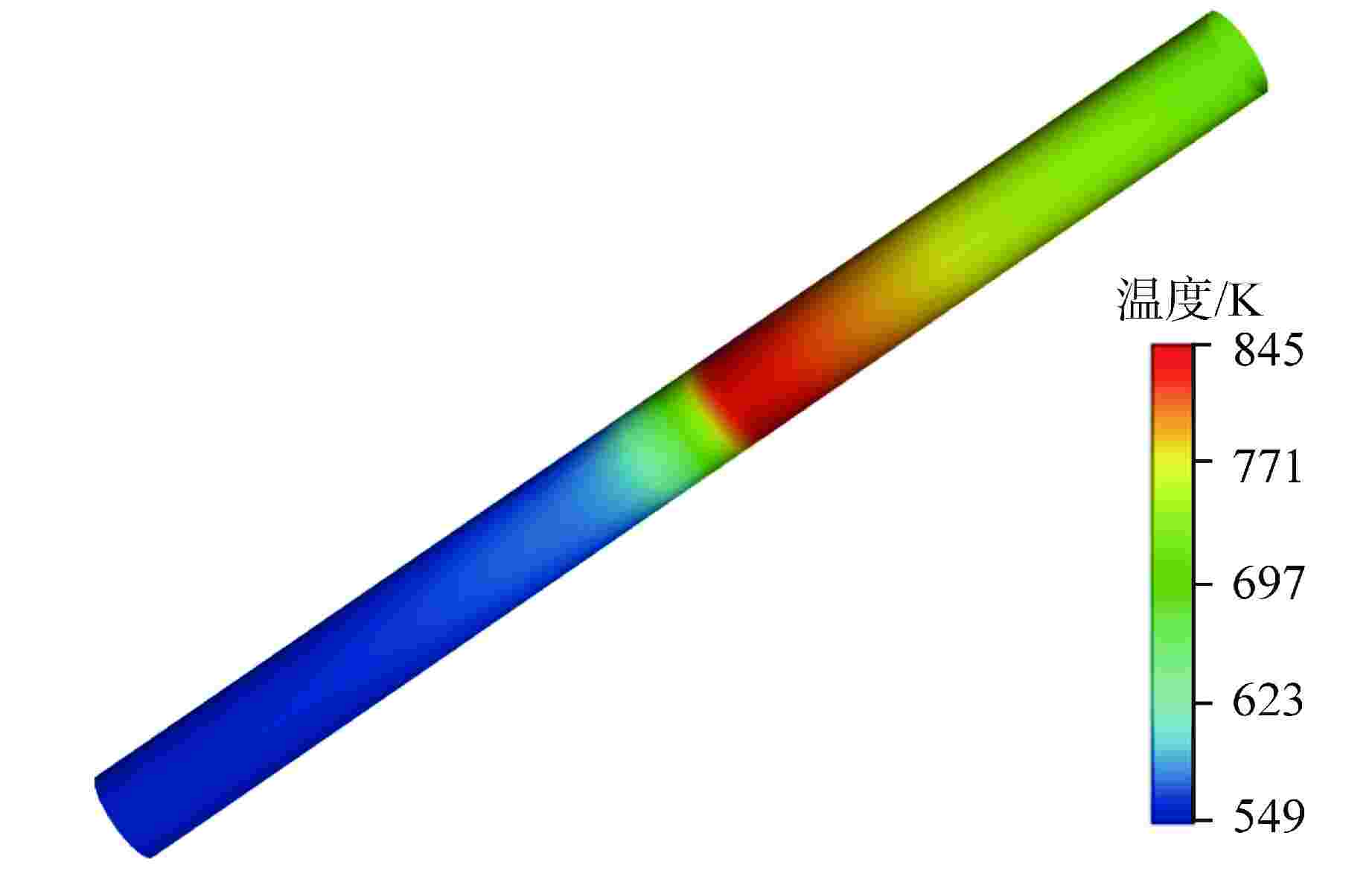
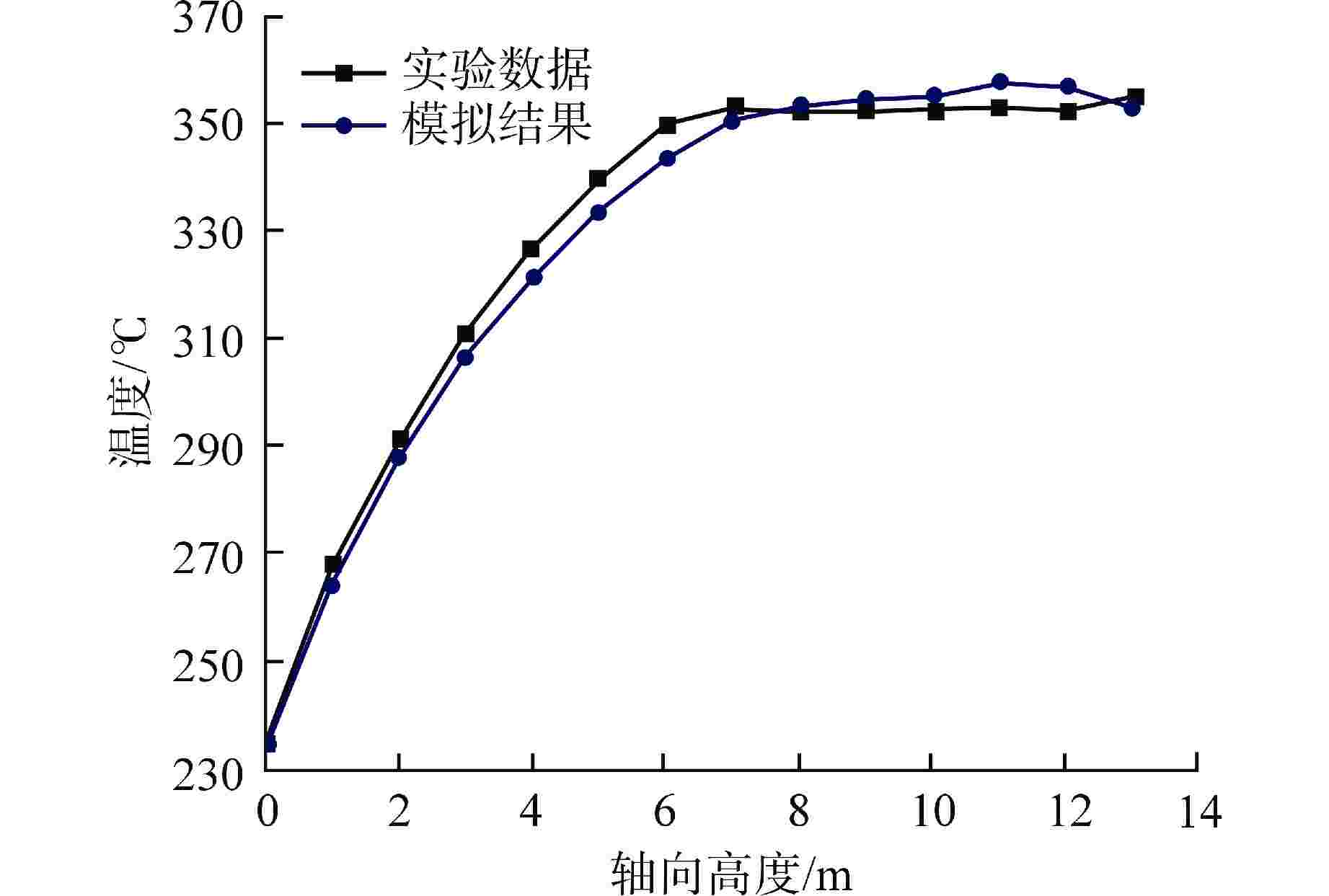
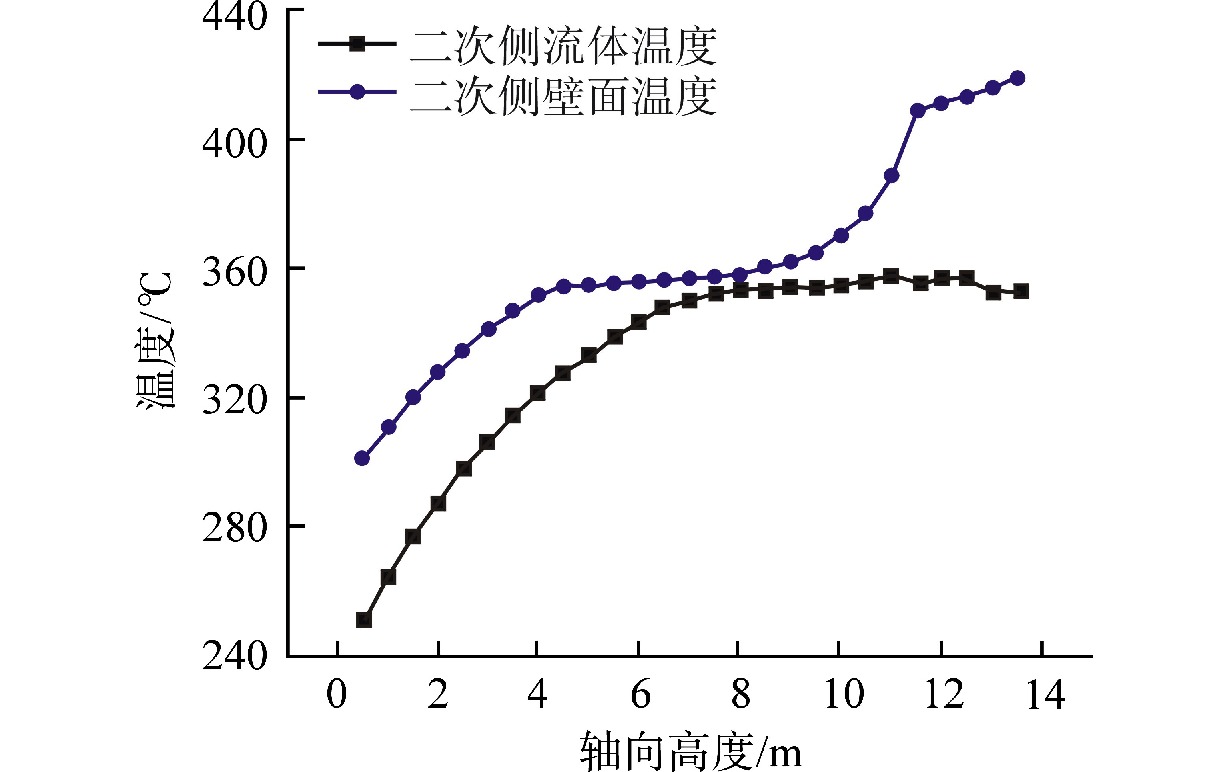
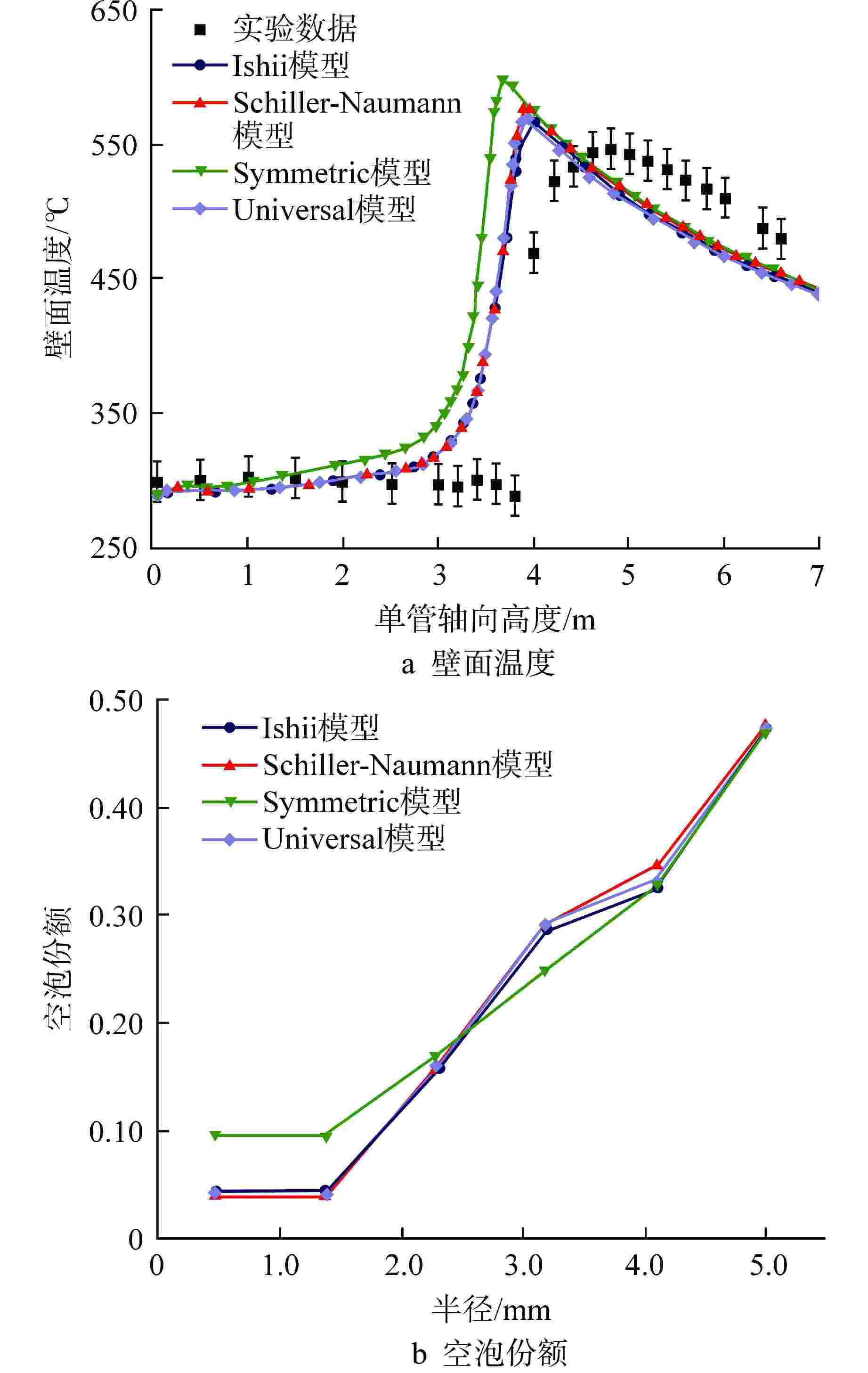
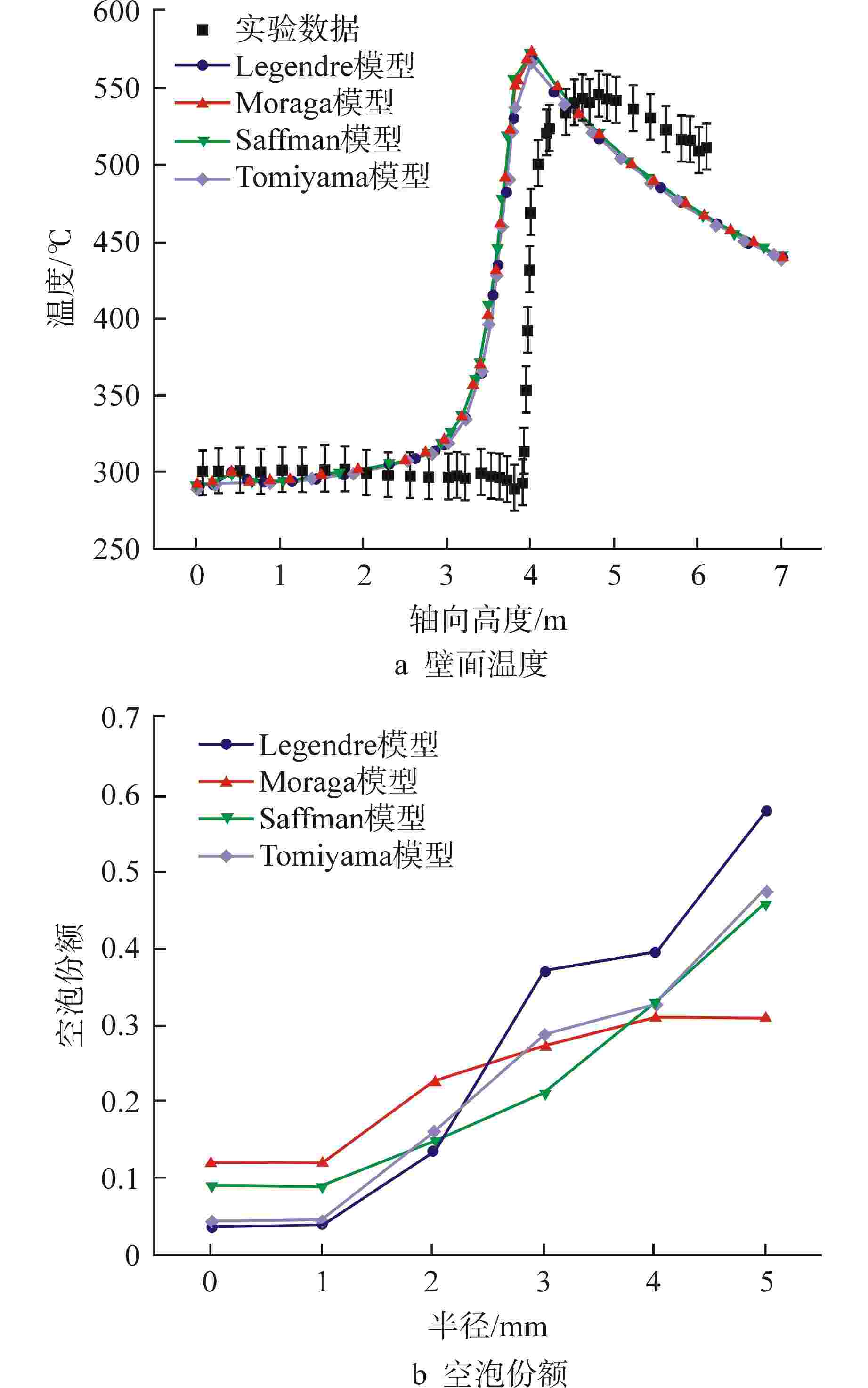
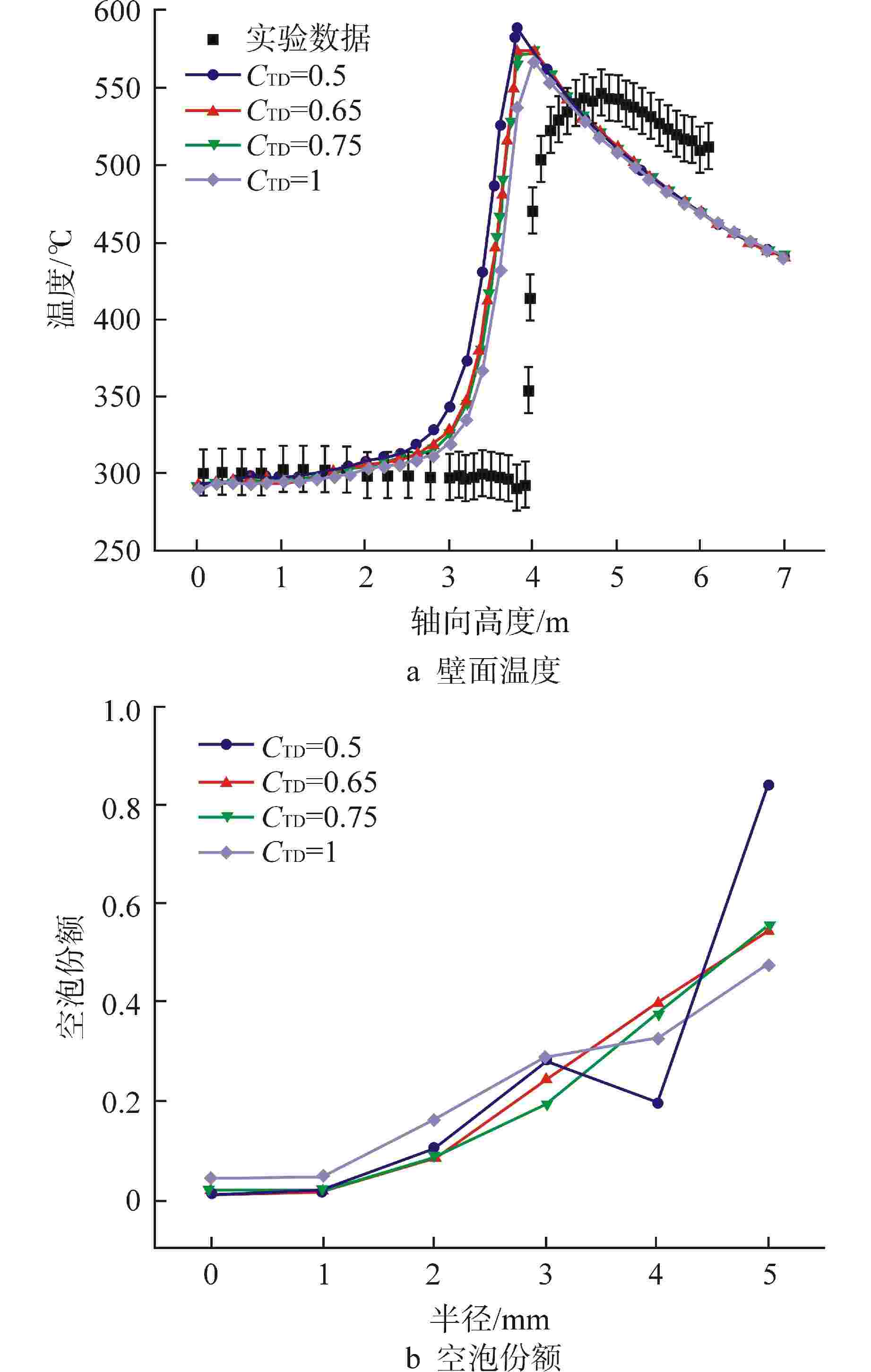
摘要: 针对直流蒸汽发生器（OTSG）中全流型沸腾传热及一、二次侧耦合换热等复杂物理现象，计算流体动力学（CFD）数值分析普遍面临计算难度大、计算效率低及不确定性大等问题。基于欧拉两流体多相流模型与临界热流密度（CHF）壁面沸腾模型，建立了管内全流型流动沸腾传热数值分析模型，并验证了模型的有效性。基于所验证的模型，开展了数值模型在多管耦合传热下的应用特性研究，明确了该数值模拟方法在多管耦合下的可靠性，并对温度与相分布计算结果对相间作用力模型的敏感性进行了数值分析。研究结果表明：基于欧拉两流体多相流模型与CHF壁面沸腾模型，能够较准确地预测管内水介质由过冷到过热的全流型流动沸腾传热过程，计算的“干涸”点位置及壁面峰值温度与实验值符合较好，最大误差小于10%；基于欧拉两流体多相流模型与CHF壁面沸腾模型的数值方法对多管耦合工况有较好的适用性，计算的二次侧温度与实验结果吻合良好；两相间曳力对壁面温度及空泡份额的计算结果有较明显的影响，但非曳力对壁面温度的影响较小，因此对于大规模工程应用计算，可在分析中不考虑部分相间非曳力的影响。本文研究结果可为OSTG的三维精细化数值分析的模型选择提供有益参考。
-
关键词:
- 直流蒸汽发生器（OSTG） /
- 欧拉两流体多相流模型 /
- 流动沸腾 /
- 耦合换热 /
- 数值模拟
Abstract: Aiming at the problems of high difficulty in simulation, low computational efficiency, and large uncertainties when applying the method of computational fluid dynamics (CFD) to the analysis of coupled heat transfer on primary and secondary sides and full-regime flow boiling heat transfer in once-through steam generator (OTSG), based on the Eulerian two-fluid multiphase model and the critical heat flux density (CHF) wall boiling model, a numerical analysis model of the full-regime flow boiling heat transfer in the tube is established, and the effectiveness of the model is verified. Based on the verified model, the application characteristics of the numerical model under multi-tube coupling heat transfer are studied, the reliability of the numerical simulation method under multi-tube coupling is clarified, and the sensitivity of the calculation results of temperature and phase distribution to the interphase force model is numerically analyzed. The results show that based on Euler's two-fluid multiphase flow model and CHF wall boiling model, the full-regime flow boiling heat transfer process of water in the tube from supercooling to overheating can be predicted accurately. The location of dry-out point and the peak temperature of the wall are in good agreement with the experimental values, with a maximum error of less than 10%. The numerical method based on Euler two-fluid multiphase flow model and CHF wall boiling model has good applicability to multi-tube coupling conditions, and the calculated secondary side temperature is in good agreement with the experimental results. The interphase drag force has obvious influence on the calculation results of wall temperature and cavitation share, but the non-drag force has little influence on wall temperature. Therefore, for large-scale engineering application calculation, the influence of some interphase non-drag forces may not be considered in the analysis. The results of this paper can provide useful reference for the model selection of OSTG's three-dimensional refined numerical analysis.-
Key words:
- OSTG /
- Eulerian two-fluid multiphase model /
- Flow boiling /
- Coupled heat transfer /
- Numerical simulation
-
图 2 壁面温度及质量含气率沿轴向高度变化
Figure 2. Variation of Wall Temperature and Mass Quality along Axial Height
图 6 多管耦合情况下二次侧流体温度
Figure 6. Secondary Side Fluid Temperature under Multi-Tube Coupling
图 7 多管耦合下二次侧流体与壁面温度变化
Figure 7. Variation of Secondary Side Fluid and Wall Temperatures under Multi-tube Coupling
图 8 曳力系数模型对计算结果的影响
Figure 8. Influence of Drag Coefficient Model on Calculation Results
图 10 壁面润滑力模型对计算结果的影响
Figure 10. Influence of Wall Lubrication Force Model on Calculation Results
图 11 湍流耗散力系数模型对计算结果的影响
Figure 11. Influence of Turbulent Dispersion Force Model on Calculation Results
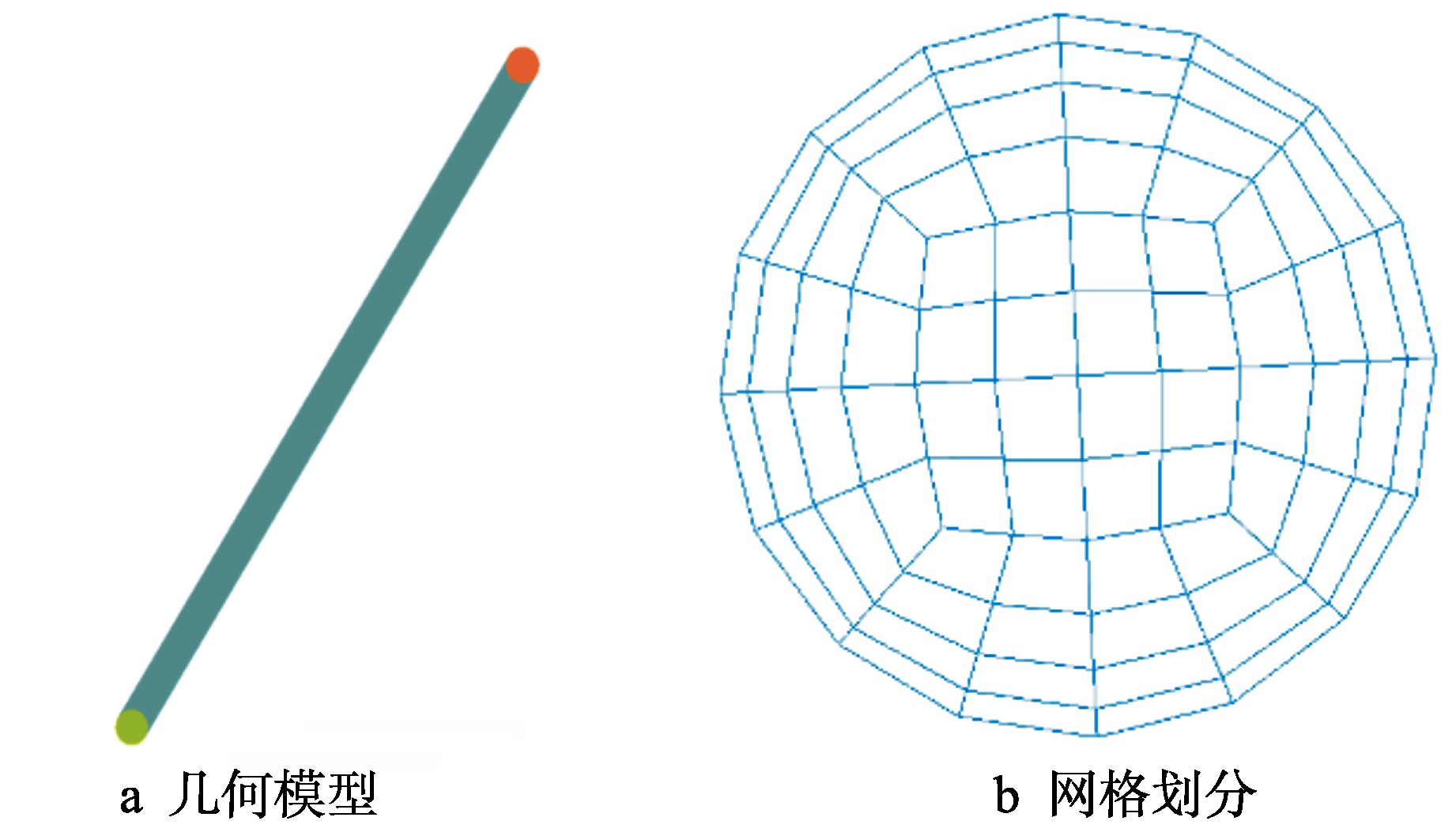
表 1 圆管几何模型与实验工况
Table 1. Geometric Model of Circular Tube and Experimental Conditions
参数 圆管轴
向高度/m管内径/
mm入口过
冷度/K系统压
力/MPa质量流速/
(kg·m−2·s−1)壁面热流密度/
(kW·m−2)数值 7 10 10 7.02 14.95 797 
下载: 导出CSV
表 2 几何模型尺寸与设计参数
Table 2. Geometric Model Size and Design Parameters
参数 设计值 管外径/mm 17.2 壁厚/mm 2.3 管节距/mm 32 轴向高度/m 14 外壳直径/mm 164 钠侧系统压力/MPa 0.1 水侧系统压力/MPa 17.2 钠侧质量流量/(kg·s−1) 25.6 水侧质量流量/(kg·s−1) 2.45
下载: 导出CSV
-
[1] 孙中宁,阎昌琪. 核动力设备[M]. 哈尔滨: 哈尔滨工程大学出版社,2004: 20-23. [2] 王冲. 中国实验快堆蒸汽发生器稳态特性分析及热工水力设计[D]. 大连: 大连理工大学,2013. [3] CONG T L, TIAN W X, QIU S Z, et al. Study on secondary side flow of steam generator with coupled heat transfer from primary to secondary side[J]. Applied Thermal Engineering, 2013, 61(2): 519-530. doi: 10.1016/j.applthermaleng.2013.08.024 [4] 干依燃,孙宝芝,齐洪亮,等. 基于传热分区的直流蒸汽发生器换热性能仿真[J]. 化工学报,2015, 66(Z1): 123-129. [5] 张振国,李小畅,谭思超,等. 钠冷快堆直流蒸汽发生器跨尺度耦合分析[J]. 原子能科学技术,2022, 56(11): 2354-2364. [6] TALEBI S, KAZEMINEJAD H, DAVILU H. Prediction of dryout and post-dryout wall temperatures using film thickness model[J]. Nuclear Engineering and Design, 2012, 244: 73-82. doi: 10.1016/j.nucengdes.2011.12.032 [7] LI H P, ANGLART H. Prediction of dryout and post-dryout heat transfer using a two-phase CFD model[J]. International Journal of Heat and Mass Transfer, 2016, 99: 839-850. doi: 10.1016/j.ijheatmasstransfer.2016.04.021 [8] ZHANG H B, HEWITT G F. Phenomenological modelling of CHF in annular flow in annuli using new models of droplet deposition and entrainment[J]. Nuclear Engineering and Design, 2016, 305: 284-292. doi: 10.1016/j.nucengdes.2016.05.029 [9] ZHANG R, CONG T L, TIAN W X, et al. Prediction of CHF in vertical heated tubes based on CFD methodology[J]. Progress in Nuclear Energy, 2015, 78: 196-200. doi: 10.1016/j.pnucene.2014.10.001 [10] MALI C R, VINOD V, PATWARDHAN A W. Comparison of phase interaction models for high pressure subcooled boiling flow in long vertical tubes[J]. Nuclear Engineering and Design, 2017, 324: 337-359. doi: 10.1016/j.nucengdes.2017.09.010 [11] MALI C R, VINOD V, PATWARDHA A W. New methodology for modeling pressure drop and thermal hydraulic characteristics in long vertical boiler tubes at high pressure[J]. Progress in Nuclear Energy, 2019, 113: 215-229. doi: 10.1016/j.pnucene.2019.01.026 [12] SHI J X, SUN B Z, ZHANG G L, et al. Prediction of dryout and post-dryout wall temperature at different operating parameters for once-through steam generators[J]. International Journal of Heat and Mass Transfer, 2016, 103: 66-76. doi: 10.1016/j.ijheatmasstransfer.2016.07.027 [13] KURUL N, PODOWSKI M Z. On the modeling of multidimensional effects in boiling channels[C]//27th National Heat Transfer Conference. Minneapolis, Minnesota, USA: ANS, 1991: 28-31. [14] IOILEV A, SAMIGULIN M, USTINENKO V, et al. Advances in the modeling of cladding heat transfer and critical heat flux in boiling water reactor fuel assemblies[C]//Proceedings of 12th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH-12). US: Pittsburgh, 2007: 1-16. [15] 李小畅,郜冶. 压水堆子通道欠热沸腾数值验证及交混翼研究[J]. 原子能科学技术,2013, 47(12): 2208-2215. [16] 李小畅. 棒束通道单相及两相流动与传热数值研究[D]. 哈尔滨: 哈尔滨工程大学,2015. [17] 霍飞鹏,陈纲,丁炜堃,等. 用CFD方法评价低压过冷沸腾相间传递模型[J]. 高技术通讯,2015, 25(7): 734-745. [18] DE BERTODANO L. Turbulent bubbly two-phase flow in a triangular duct[D]. Troy: Rensselaer Polytechnic Institute, 1991. [19] ANTAL S P, LAHEY R T JR, FLAHERTY J E. Analysis of phase distribution in fully developed laminar bubbly two-phase flow[J]. International Journal of Multiphase Flow, 1991, 17(5): 635-652. doi: 10.1016/0301-9322(91)90029-3 [20] BECKER K M, LING C H, HEDBERG S, et al. An experimental investigation of post dryout heat transfer: KTH-NEL-33[R]. Sweden: Dept. of Reactor Technology, 1983. [21] MURALLIDHARAN J S, PRASAD B V S S S, PATNAIK B S V, et al. CFD investigation and assessment of wall heat flux partitioning model for the prediction of high pressure subcooled flow boiling[J]. International Journal of Heat and Mass Transfer, 2016, 103: 211-230. doi: 10.1016/j.ijheatmasstransfer.2016.06.050 [22] EGOROV Y, MENTER F. Experimental Implementation of the RPI Wall Boiling Model in CFX-5.6: TR-04-10[R]. Pennsylvania: ANSYS GmbH, 2004. [23] NANDAKUMAR R, SELVARAJ P, ATHMALINGAM S, et al. Thermal simulation of sodium heated once through steam generator for a fast reactor[J]. International Journal of Advances in Engineering Sciences and Applied Mathematics, 2012, 4(3): 127-137. doi: 10.1007/s12572-012-0063-1 [24] VINOD V, SIVAKUMAR L S, KUMAR V A S, et al. Experimental evaluation of the heat transfer performance of sodium heated once through steam generator[J]. Nuclear Engineering and Design, 2014, 273: 412-420. doi: 10.1016/j.nucengdes.2014.03.034 -
计量
- 文章访问数: 441
- HTML全文浏览量: 31
- PDF下载量: 45
- 被引次数: 0
