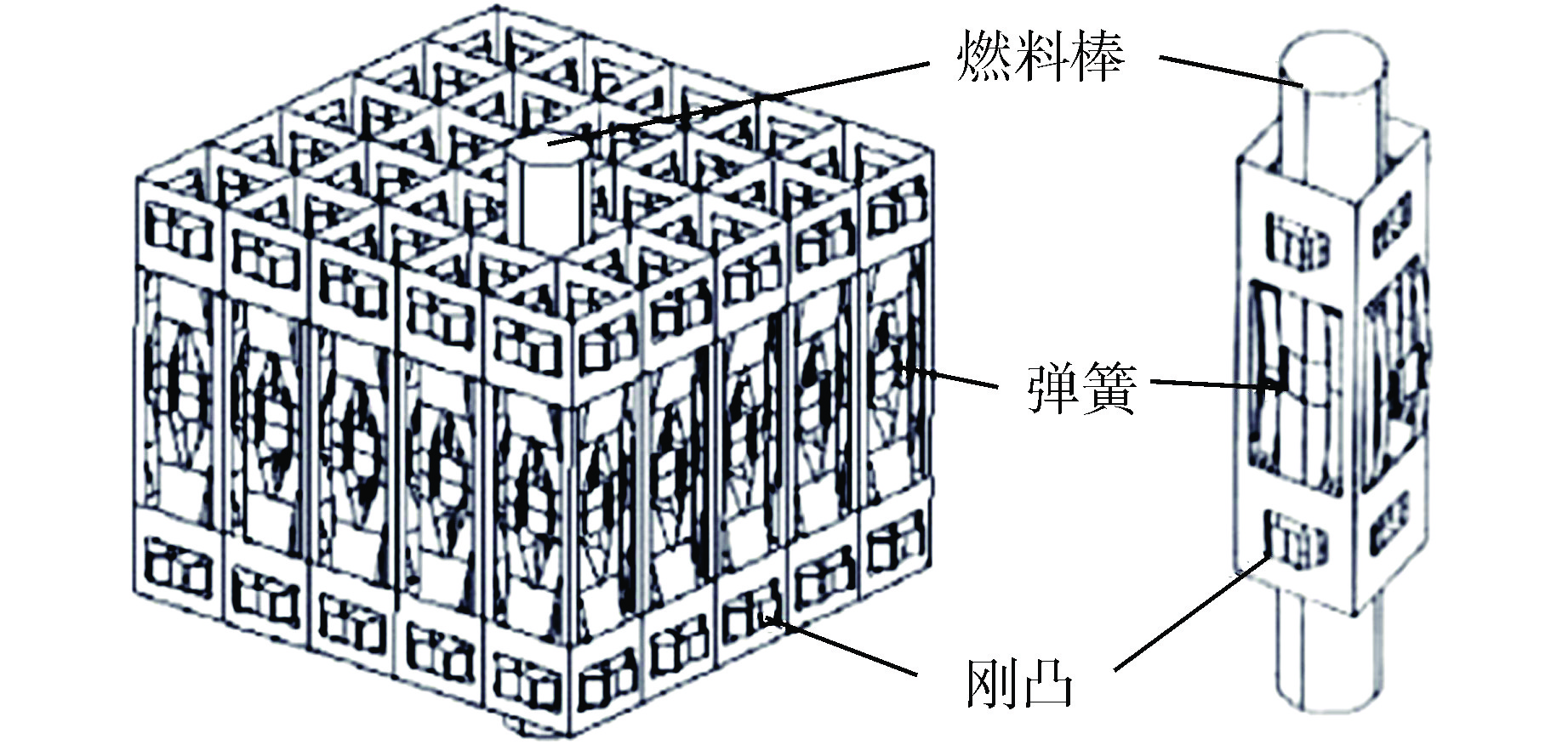
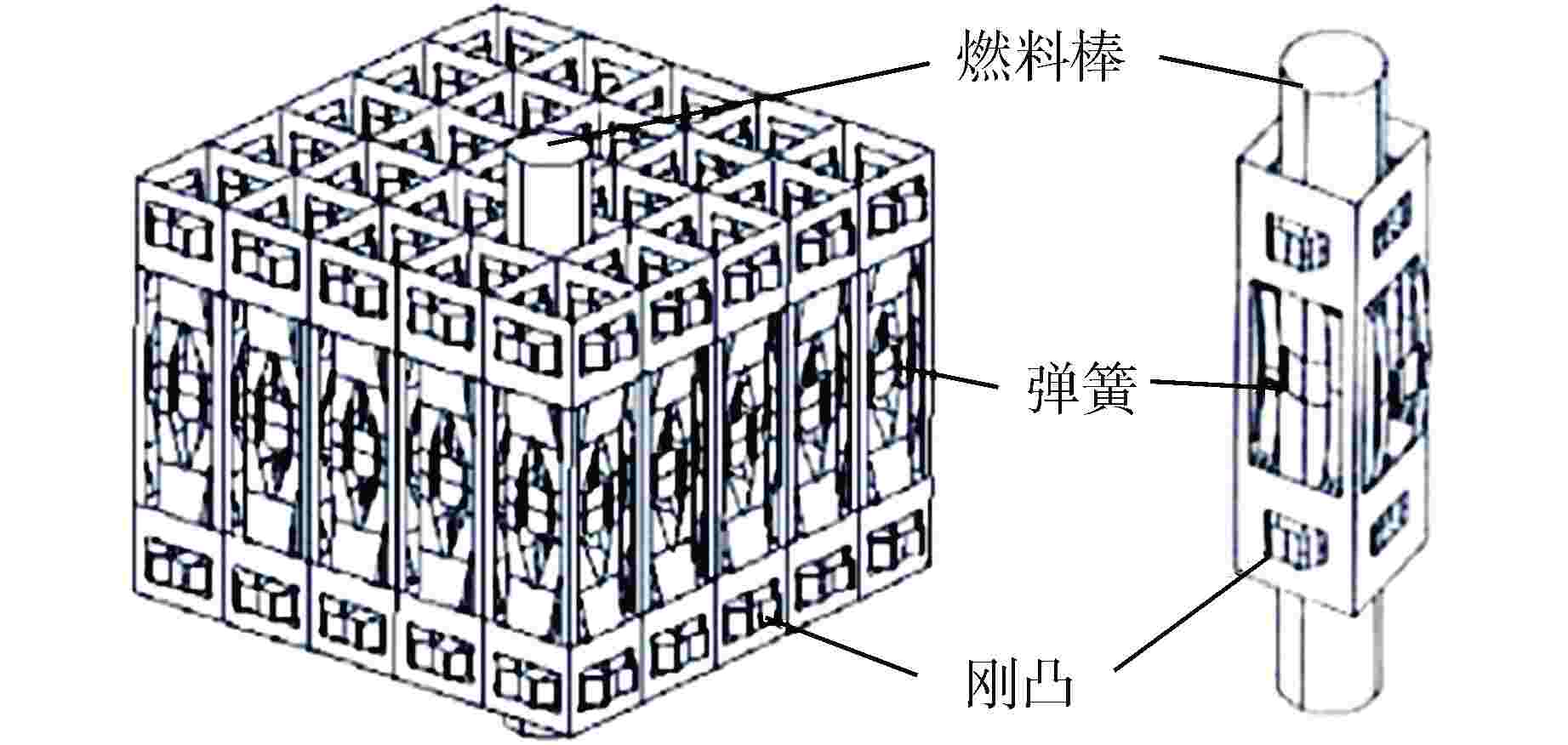
Model Analysis of Fuel Assembly Grid Spring Stiffness
-
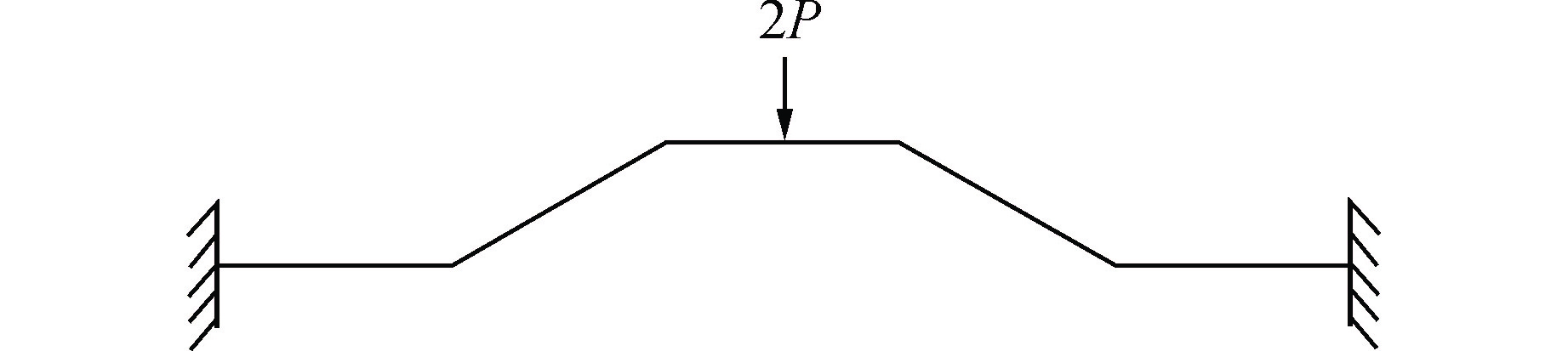
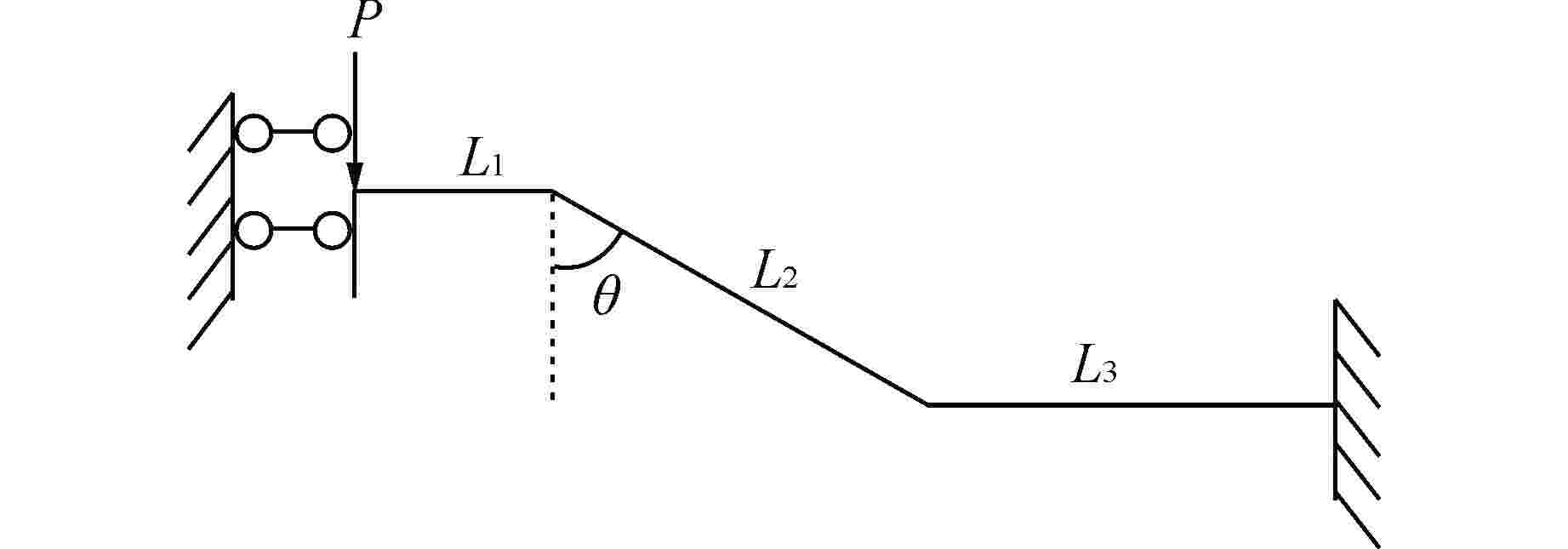
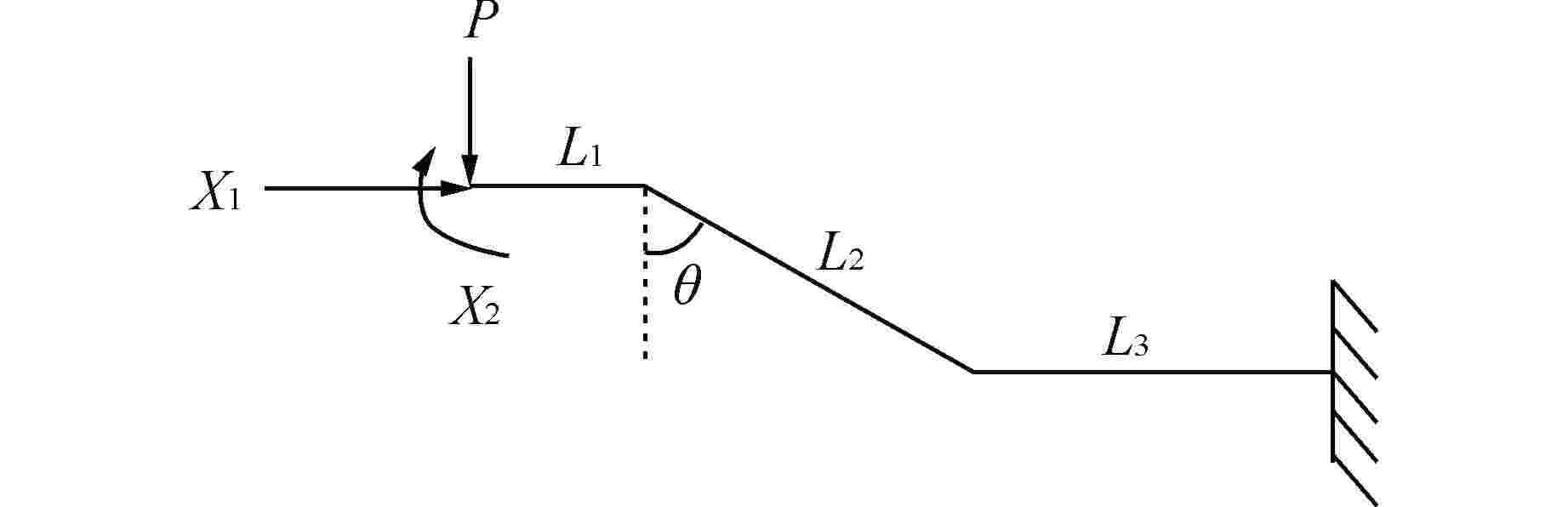
摘要: 格架弹簧是压水堆燃料组件的关键零部件，其为燃料棒提供夹持功能。刚度是格架弹簧的关键特性，其关系到燃料棒的堆内运行性能。本文基于格架弹簧的结构以及受力特点，给出了格架弹簧的受力分析模型，并推导了理论刚度计算公式，即得到了格架弹簧的理论刚度模型。另外，在商业有限元软件ABAQUS中建立了多种尺寸格架弹簧实体结构的有限元刚度模型，并计算获得了格架弹簧的变形量以及刚度曲线。通过有限元结果与理论刚度模型结果的对比，证明了理论刚度模型的合理性，并分析讨论了理论刚度模型的优缺点。本文首次提出的格架弹簧理论刚度模型可用于代替格架方案设计期间的有限元迭代过程，并能快速获得优化方案的主要设计尺寸。但本文分析方法不能替代实验，在方案固化后仍需开展实验确定格架弹簧的刚度。本文得到的格架弹簧理论模型可为燃料组件格架弹簧参数的快速优化设计提供新的思路。Abstract: Grid spring is a critical component of PWR fuel assembly, which provides clamp function for the fuel rod. Stiffness is a critical characteristic of grid spring, which is related to the in-pile operational performance of the fuel rod. According to the grid spring structure and mechanical characteristics, this paper proposes a mechanical analysis model of the grid spring, and the theoretical stiffness calculation formula is obtained through deduction, and the grid spring theoretical stiffness model is also obtained. Furthermore, the finite element stiffness models of grid spring with various sizes are established in the commercial finite element code ABAQUS, and the deformation and stiffness curves of grid spring are obtained by calculation. By comparison between the FEM analysis results and the theoretical calculation ones, the rationality of the theoretical stiffness model is proved, and then the advantages and shortcomings of the theoretical stiffness model are analyzed. The theoretical stiffness model of grid spring proposed for the first time in this paper can be used to replace the finite element iterative process during the design of grid scheme, and the main design dimensions of the optimized scheme can be obtained quickly. However, the theoretical method in this paper cannot replace the experiments, and tests are still needed to determine the stiffness of the grid spring after the scheme is solidified. The grid spring theoretical model in this paper provides a new idea to quickly optimize the fuel assembly grid spring design.
-
Key words:
- Fuel assembly /
- Grid spring /
- Stiffness /
- Theoretical stiffness model /
- Finite element method (FEM)
-
图 4 格架弹簧静定结构受力分析模型
Figure 4. Determinate Structure Mechanical Analysis Model for Grid Spring
图 7 格架弹簧有限元模拟的刚度曲线
Figure 7. Stiffness Curve by Grid Spring Finite Element Method Simulation
表 1 格架弹簧实体模型尺寸参数
Table 1. Dimensional Parameters of Grid Spring Solid Model
参数 2L1/mm L2/mm L3/mm 2P/N θ/rad b/mm h/mm 模型1 2.06 3.65 3.83 40 1.2 5.5 0.3 模型2 4 3.65 3.83 40 1.2 5.5 0.3 模型3 4 3 5 40 1.2 5.5 0.3 模型4 5 3 5 40 1.2 5.5 0.3 b—宽度；h—高度 
下载: 导出CSV
表 2 理论刚度模型与有限元模拟结果对比
Table 2. Comparison of Theoretical Stiffness Model and Finite Element Simulation Results
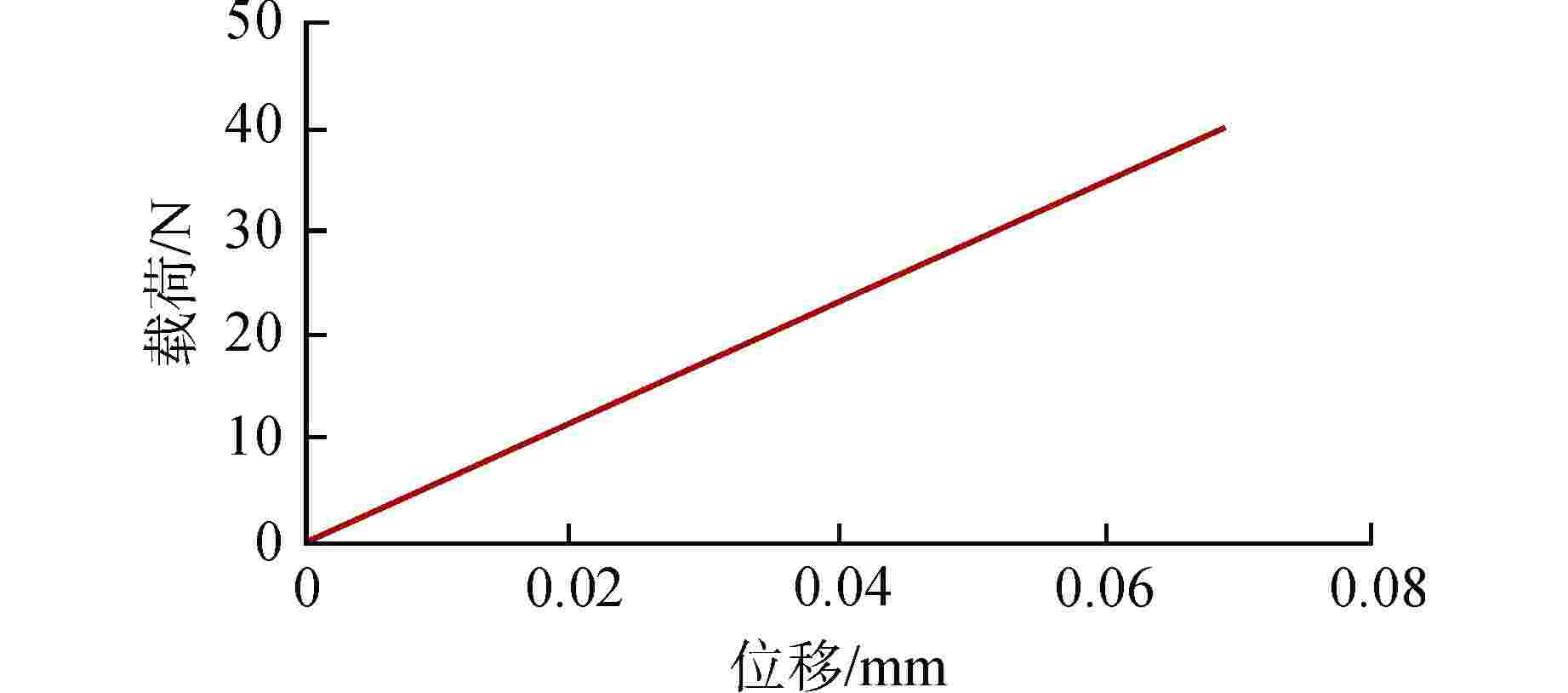
模型 对比参数 有限元模拟结果 理论刚度模型结果 相对偏差/% 1 位移/mm 0.0689 0.0607 11.9 刚度/(N·mm−1) 581 659 13.4 2 位移/mm 0.0756 0.0654 13.5 刚度/(N·mm−1) 529 612 15.7 3 位移/mm 0.1357 0.1225 9.7 刚度/(N·mm−1) 287 326 13.6 4 位移/mm 0.2476 0.2143 13.4 刚度/(N·mm−1) 162 187 15.4
下载: 导出CSV
-
[1] 国家核安全局. 核动力厂设计安全规定: HAF 102-2016[S]. 北京: 环境保护部办公厅,2016: 6. [2] IAEA. Review of fuel failures in water cooled reactors: IAEA Nuclear Energy Series No. NF-T-2.1[R]. Vienna: IAEA, 2010. [3] 杜光彦,张世权. 压水堆燃料组件方形定位格架结构设计、工艺特点和性能评价[J]. 核动力工程,1987, 8(3): 65-73. [4] FERRARI G, KARAZIS K, AMABILI M. Experiments on the localized interaction at the interface fuel rod/spacer grid in pressurized water reactors[J]. Nuclear Engineering and Design, 2022, 399: 111998. doi: 10.1016/j.nucengdes.2022.111998 [5] 任全耀,陈杰,赵瑞瑞,等. 新型定位格架夹持结构的力学特性研究[J]. 原子能科学计算,2020, 54(12): 2411-2417. [6] 蒋跃元,徐勇. NHR-200定位格架的设计研究[J]. 清华大学学报: 自然科学版,1996, 36(11): 6-11. [7] 王淅铖,王鼎渠,蒋跃元,等. NHR200-II燃料组件定位格架简化建模方法研究[J]. 核动力工程,2021, 42(4): 105-111. [8] 吴先洋,蒋跃元,王鼎渠,等. NHR200-II定位格架整体承载能力试验研究[J]. 核科学与工程,2015, 35(3): 424-433. [9] 蒋跃元,施继斌,徐勇. 供热堆格架力学性能试验研究[J]. 核动力工程,2007, 28(1): 22-25,31. [10] SHIN M K, LEE H A, LEE J J, et al. Optimization of a nuclear fuel spacer grid spring using homology constraints[J]. Nuclear Engineering and Design, 2008, 238(10): 2624-2634. doi: 10.1016/j.nucengdes.2008.04.003 [11] KIM K S, YOON K H, SONG K N, et al. Finite element analysis of the optimized H type grid spring by using gap elements[J]. Nuclear Engineering and Design, 2008, 238(9): 2239-2244. doi: 10.1016/j.nucengdes.2008.02.025 [12] NEUPANE H, IBARRA L. Development of a spring model to predict the behavior of fuel rods in a spacer grid assembly[J]. Nuclear Engineering and Design, 2022, 394: 111826. doi: 10.1016/j.nucengdes.2022.111826 -
图(7) / 表(2)
计量
- 文章访问数: 218
- HTML全文浏览量: 56
- PDF下载量: 59
- 被引次数: 0
