Experimental Study on Gas-Liquid Counter Current Flow Limitation in Inclined Pipes
-
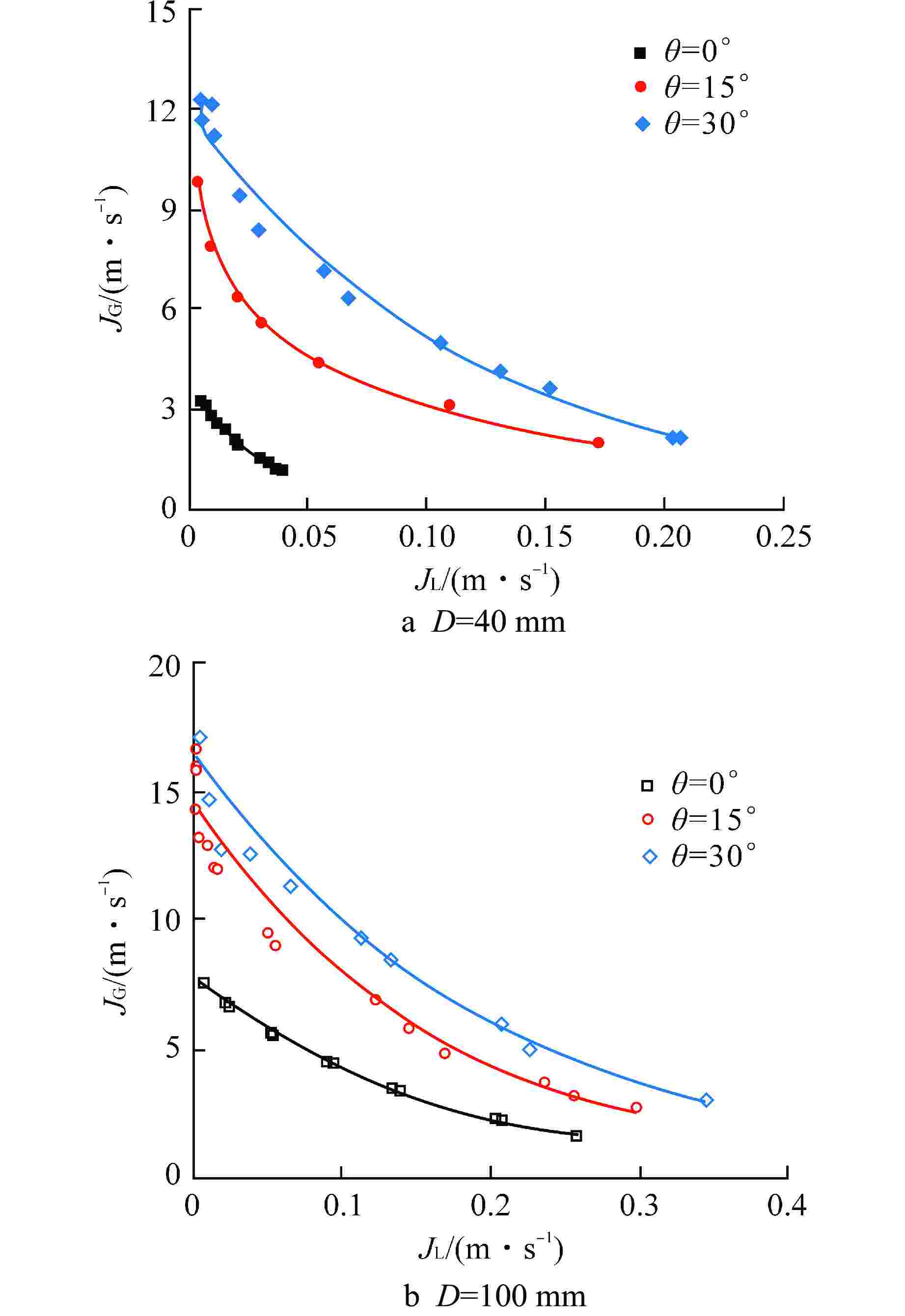
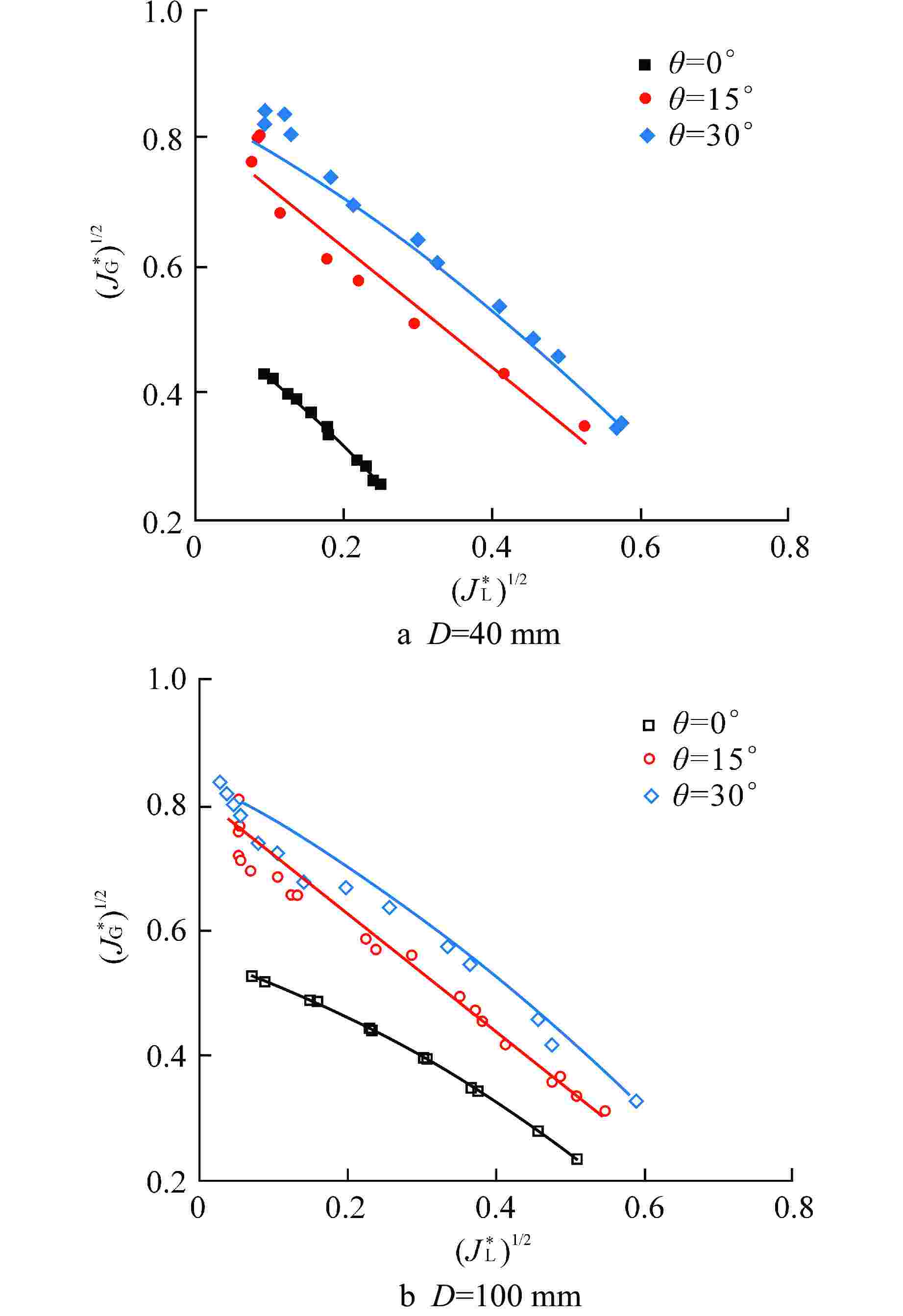
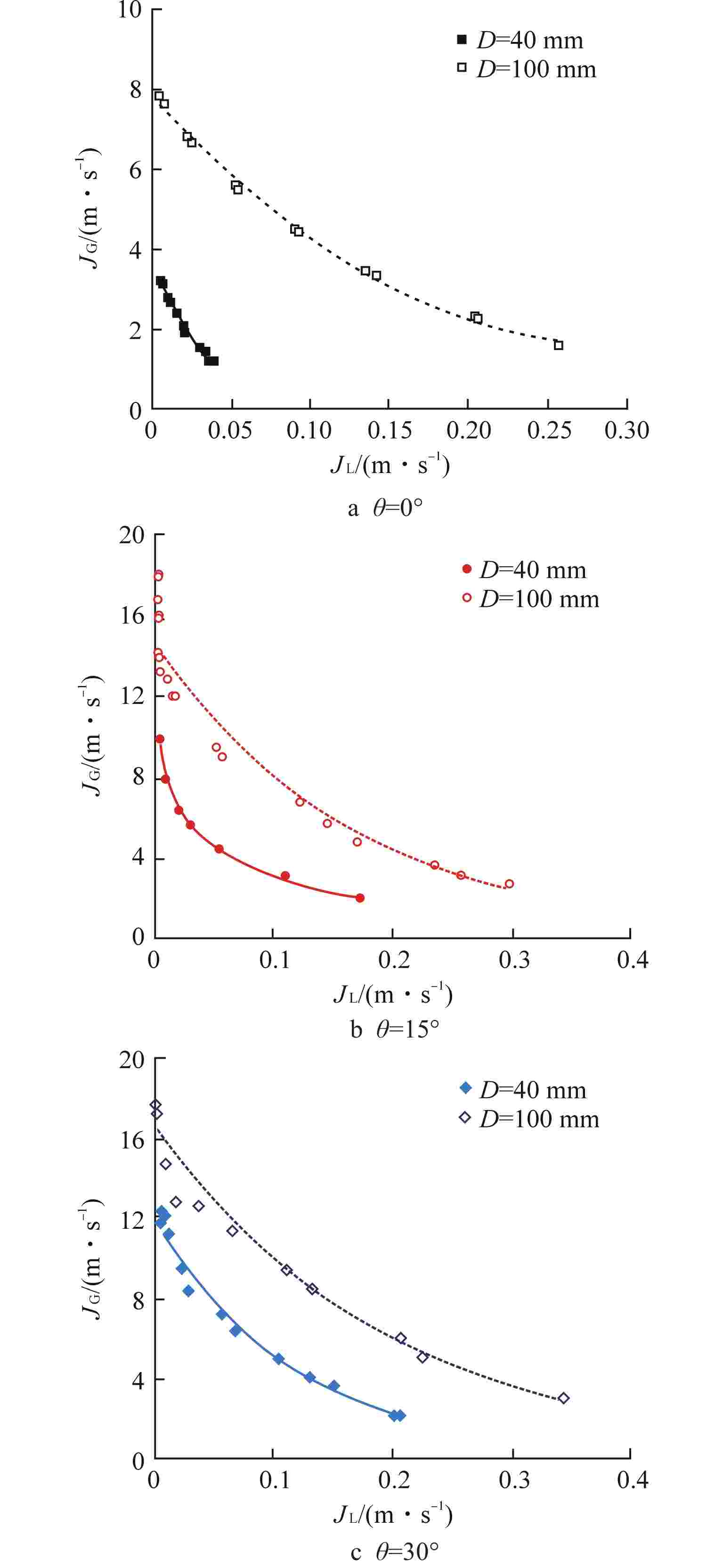
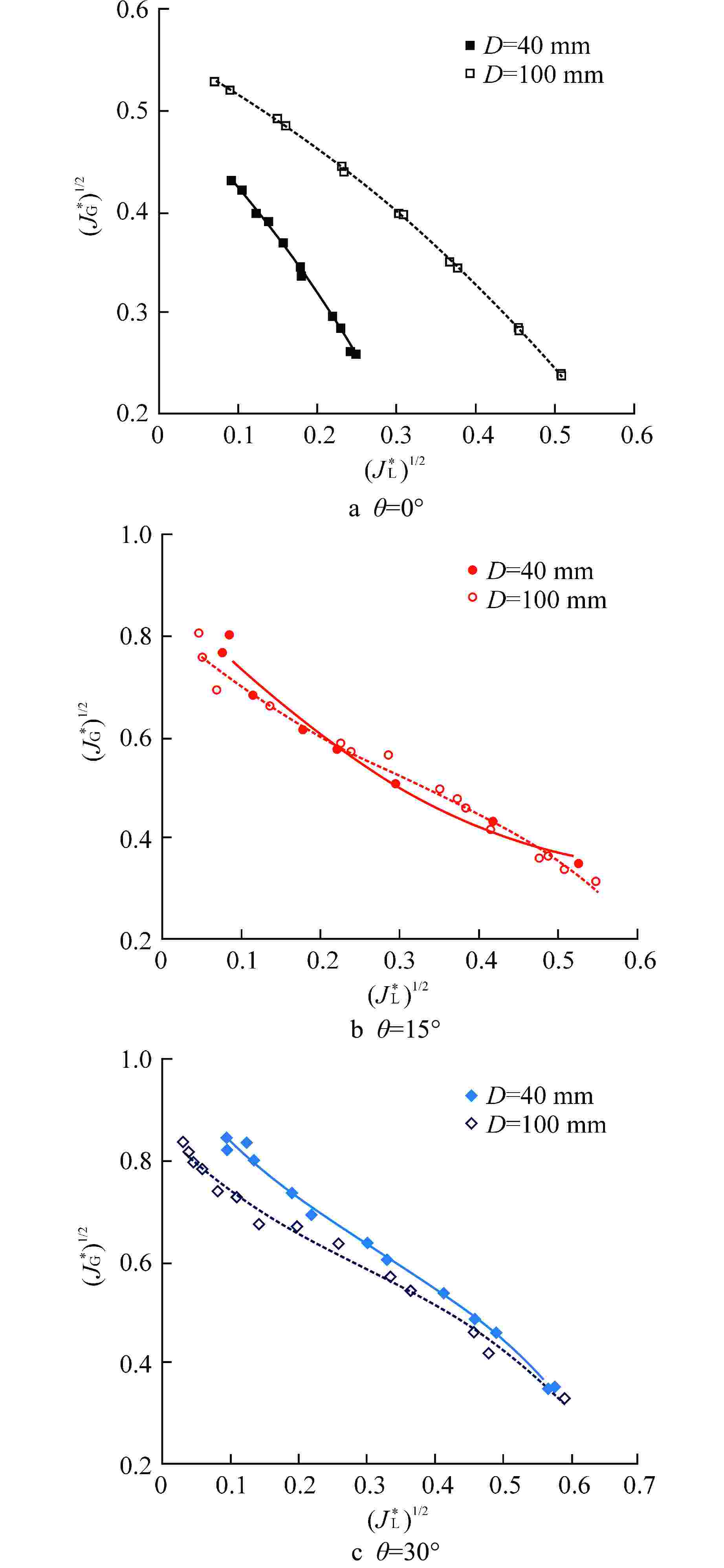
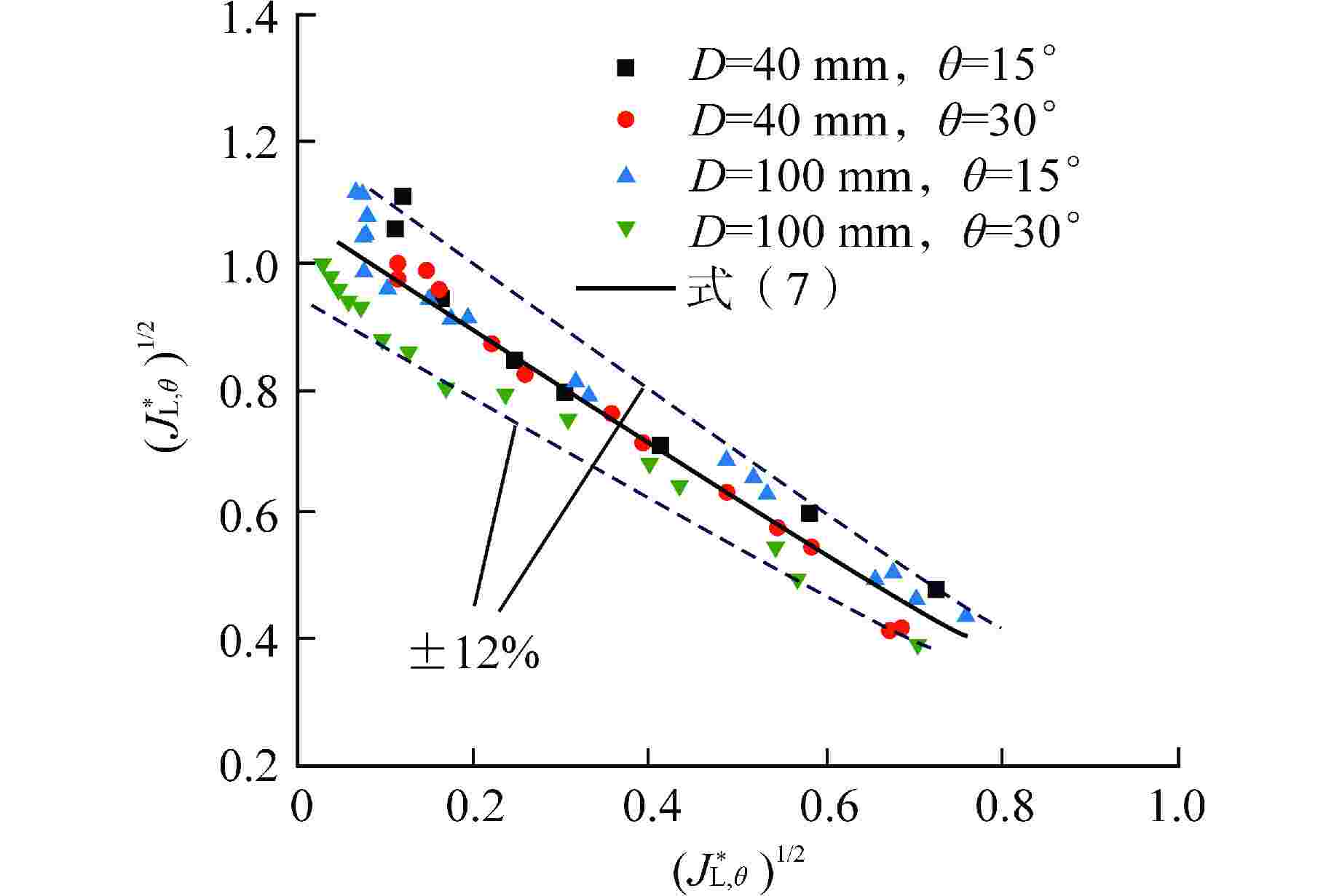
摘要: 失水事故下压水堆热段内气液两相顺利逆流对防止堆芯熔化事故至关重要，而热段是由水平管与倾斜管组合而成。为探明热段内气液逆流的约束机制，以常温空气/水为两相工质对倾斜管与水平管内气液两相逆流极限（CCFL）特性进行实验，研究了管道倾角（0°~30°）和管径（40~100 mm）对管内CCFL的影响。主要结论有：CCFL工况下，水平管内呈分层流；随管道倾角和管径增大，倾斜管内分层流逐渐过渡为雾状流；相同管径下，以表观流速表征的CCFL曲线随管道倾角增大而升高，意味着热段内气液逆流主要受水平段控制；相同管道倾角下，倾斜管与水平管的CCFL表观流速曲线均随管径增大而升高；传统Wallis参数未反映管道倾角对CCFL的影响，也未能准确表征管径对水平管CCFL的影响，但Wallis参数可良好关联管径对倾斜管CCFL的影响；提出了可同时关联管道倾角与管径影响的倾斜管CCFL实验关联式。研究结果对压水堆核电厂的安全性分析提供了基础数据和实验关联式。
-
关键词:
- 压水堆 /
- 失水事故 /
- 气液两相逆流极限（CCFL） /
- 倾斜管 /
- 管径效应
Abstract: The smooth countercurrent of gas and liquid phases in the hot leg of pressurized water reactor (PWR) is very important to prevent the core melting accident, and the hot leg is composed of horizontal pipe and inclined pipe. In order to determine the constraint mechanism of gas-liquid countercurrent in the hot leg, experiments were carried out on the characteristics of countercurrent flow limitation (CCFL) in inclined and horizontal pipes with ambient air/water as two-phase working medium, and the effects of pipe layout inclination angle (0°~30°) and pipe diameter (40~100 mm) on CCFL in the pipes were studied. The main conclusions are as follows: under the CCFL conditions, the flow pattern in the horizontal pipe shows a typical stratified flow; in the inclined pipe, as the inclination angle and diameter of the pipe increase, stratified flow gradually transits to mist flow. At the same pipe diameter, the CCFL curve characterized by superficial velocities increases with the increase of pipe inclination, which indicates that the gas-liquid countercurrent flow in the hot leg is mainly controlled by the horizontal section. At the same pipe inclination angle, the CCFL curves for both inclined and horizontal pipes increase with the increase of pipe diameter. The conventional Wallis parameters do not reflect the effect of pipe inclination on the CCFL, and also fail to accurately characterize the effect of pipe diameter on the CCFL of horizontal pipes; however, they can correlate the effect of pipe diameter on the CCFL of inclined pipes satisfactorily. Finally, an experimental correlation, which can simultaneously correlate the effects of pipe inclination and diameter, was proposed for the CCFL of inclined pipes. The research results provide basic data and experimental correlation for the safety analysis of PWR nuclear power plant.-
Key words:
- Pressurized water reactor /
- Loss of coolant accident /
- CCFL /
- Inclined pipe /
- Diameter effect
-
图 1 实验系统图
QG―空气流量；pG1―流量计处空气压力；pG2―排气管入口空气压力；TG―空气温度；TL―水温度；ΔH―低位水箱水位高度
Figure 1. Schematic of the Experimental System
图 2 倾斜管内气液逆向流动极限实况
Figure 2. Scenes of Gas-liquid Countercurrent Flow Limitation in Inclined Pipes
图 3 不同管道倾角下的表观流速CCFL实验结果
Figure 3. Experimental Results of CCFL Characterized by Superficial Velocities at Different Pipe Inclinations
图 4 不同管道倾角下的Wallis参数CCFL实验结果
Figure 4. Experimental Results of CCFL Characterized by Wallis Parameters at Different Pipe Inclinations
图 5 不同管道直径下的表观流速CCFL实验结果
Figure 5. Experimental Results of CCFL Characterized by Superficial Velocities at Different Pipe Diameters
图 6 不同管道直径下的Wallis参数CCFL实验结果
Figure 6. Experimental Results of CCFL Characterized by Wallis Parameters at Different Pipe Diameters
图 7 本文CCFL实验结果与相关关联式预报结果的比较
Figure 7. Comparison between the Experimental CCFL Results in This Study and the Predictions of Related Correlations
图 8 基于修正的Wallis参数整理倾斜管CCFL实验结果
Figure 8. Expressing Experimental CCFL Results of Inclined Pipes Using Modified Wallis Parameters
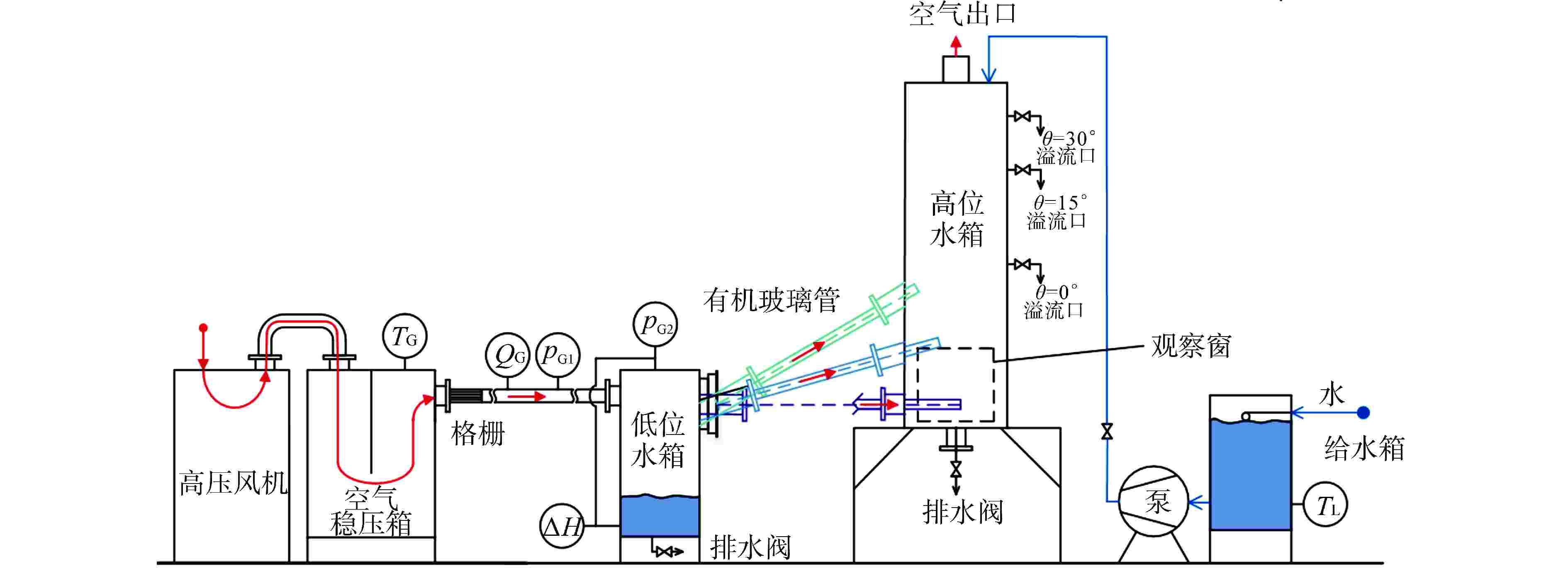
表 1 实验用仪表
Table 1. Instruments Used in the Experiment
测点参数 仪表名称 量程 精度 QG 涡街流量计 199~1990 m3·h−1 1.0级 涡街流量计 35~350 m3·h−1 1.5级 涡街流量计 5~50 m3·h−1 1.0级 pG1 压力变送器 0~100 kPa 0.2级 pG2 绝压变送器 1.3~130 kPa 0.2级 ΔH 差压变送器 0.5~10 kPa 0.2级 HL 液位变送器 0~100 kPa 0.5级 TG、TL 铂电阻 0~100℃ 0.2级 
下载: 导出CSV
表 2 实验结果的不确定度
Table 2. Uncertainties of the Experimental Results
试件编号 D/mm θ QG/(m3·h−1) 不确定度 ${J^{\;*}_{{\rm{G}}}} $/% ${J^{\;*}_{{\rm{L}}}} $/% 1 40 0° 5.2~17.4 0.97~7.17 0.14~0.25 2 40 15° 9.1~42.4 0.90~1.10 0.51~5.81 3 40 30° 9.4~55.6 0.90~8.74 0.53~1.33 4 100 0° 45.2~239.3 0.90~2.34 0.14~0.25 5 100 15° 77.6~508.3 1.93~6.35 0.45~0.88 6 100 30° 85.8~549.6 1.96~5.77 0.32~2.72
下载: 导出CSV
表 3 文献中的倾斜管CCFL关联式
Table 3. CCFL Correlations Reported in the Literature
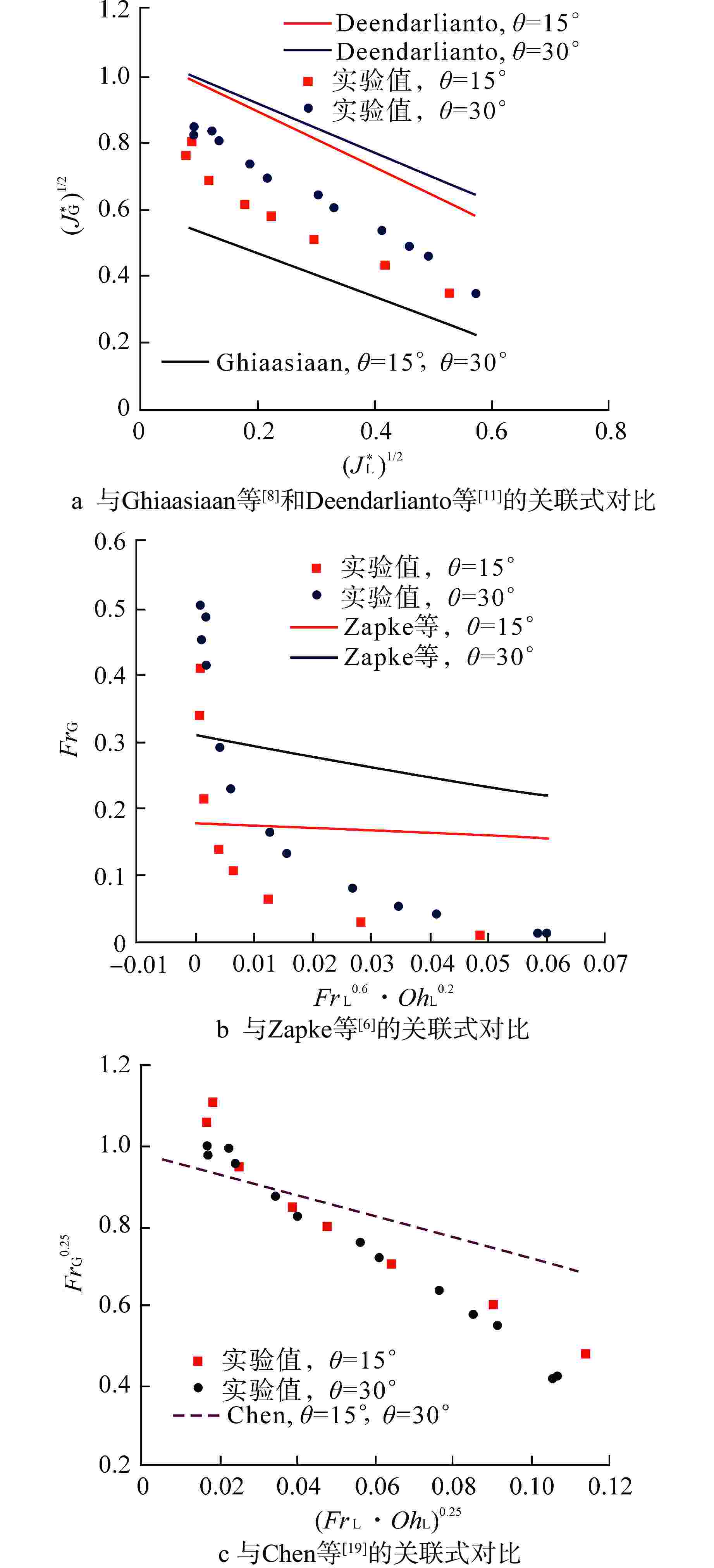
文献来源 管径（D）或流道尺寸（H和W）/mm 关联式 管道倾角 θ 工质 Ghiaasiaane等[8] D=19 $ {\left( {J_G^*} \right)^{1/2}} + 0.66{\left( {J_L^*} \right)^{1/2}} = 0.60 $ θ =30°, 45°, 75°, 90° 空气/水 Deendarlianto等[11] D=16 $ \begin{array}{c} {\left( {J_G^*} \right)^{1/2}} + m{\left( {J_L^*} \right)^{1/2}} = C \\ m = 1.14({\theta ^*})^2 - 1.21{\theta ^*} + 1.01 \\ C = 0.24\left( {{\sigma \mathord{\left/ {\vphantom {\sigma {{\sigma _{W} }}}} \right. } {{\sigma _{W} }}}} \right) + 0.82 \\ {\theta ^*} = {\theta \mathord{\left/ {\vphantom {\theta {90}}} \right. } {90}} \end{array}$ θ=30°, 45°, 60° 空气/水 Zapke等[6] H=50, W=10;
H=50, W=20;
H=100, W=10;
H=150, W=10.$ F{r_{\text{G}}} = {K_0}\exp ( - nF{r_{\text{L}}}^{0.6}O{h_{\text{L}}}^{0.2}) $
$ F{r_{{\rm{G}}}} = \dfrac{{{\rho _{\text{G}}}J_{{\rm{G}}}^2}}{{g{D_{{\mathrm{e}}}}({\rho _{\text{L}}} - {\rho _{\text{G}}})}} $; $ F{r_{\text{L}}} = \dfrac{{{\rho _{\text{L}}}J_{\text{L}}^{\text{2}}}}{{g{D_{{\mathrm{e}}}}({\rho _{\text{L}}} - {\rho _{\text{G}}})}} $; $ O{h_{{\rm{L}}}} = \sqrt {\dfrac{{\mu _{\text{L}}^2}}{{{\rho _{\text{L}}}{D_{{\mathrm{e}}}}\sigma }}}$
$ \begin{aligned} {K_0} =\; & 7.9143 \times {10^{ - 2}} + 4.9705 \times {10^{ - 3}}\theta + \\[-3pt] & 1.5183 \times {10^{ - 4}}{\theta ^2} - 1.9852 \times {10^{ - 6}}{\theta ^3}\end{aligned} $
$ \begin{aligned} n = \; & 1{\text{.8149}} \times {\text{1}}{{\text{0}}^{\text{1}}} - {\text{1}}{\text{.9471}}\theta {\text{ + 6}}{\text{.7058}}\times \\[-3pt] & {\text{1}}{{\text{0}}^{ - {\text{2}}}}{\theta ^{\text{2}}} - {\text{5}}{\text{.3227}} \times {\text{1}}{{\text{0}}^{ - {\text{4}}}}{\theta ^{\text{3}}}\end{aligned} $θ=2°, 5°, 10°, 20°, 40°, 60°, 70°, 80°, 90° 空气/水 Chen等[19] D=20 $ F{r_{{\rm{G}}}}^{1/4} = 0.98 - 2.61{(F{r_{{\rm{L}}}} \cdot O{h_{{\rm{L}}}})^{1/4}} $
$ F{r_{\text{G}}} = \dfrac{{{\rho _{\text{G}}}J_{{\rm{G}}}^2}}{{gD\sin \theta ({\rho _{\text{L}}} - {\rho _{\text{G}}})}} $; $ F{r_{{\rm{L}}}} = \dfrac{{{\rho _{\text{G}}}J_{{\rm{L}}}^2}}{{gD\sin \theta ({\rho _{\text{L}}} - {\rho _{\text{G}}})}} $;
$ O{h_{{\rm{L}}}} = \sqrt {\dfrac{{\mu _{\text{L}}^2}}{{{\rho _{\text{L}}}{D_{{\mathrm{e}}}}\sigma }}} $θ=30°, 45°, 60° 空气/水
氮蒸汽/液氮σ—流体实际表面张力，N·m−1；σw—室温下水的表面张力，N·m−1；H—流道高度，mm；W—流道宽度，mm；De—流道水力直径，m；μL—液相动力黏度，Pa·s
下载: 导出CSV
-
[1] 蔡志明,蔡章生. 核动力装置小破口失水事故的瞬态特性模拟与处置研究[J]. 核动力工程,2001, 22(4): 337-341. [2] 彭云康. 回流流动极限实验研究综述[J]. 核动力工程,1993, 14(6): 556-560. [3] GHIAASIAAN S M, WU X, SADOWSKI D L, et al. Hydrodynamic characteristics of counter-current two-phase flow in vertical and inclined channels: effects of liquid properties[J]. International Journal of Multiphase Flow, 1997, 23(6): 1063-1083. doi: 10.1016/S0301-9322(97)00027-X [4] ASTYANTO A H, INDARTO K, KIRKLAND K V, et al. An experimental study on the effect of liquid properties on the counter-current flow limitation (CCFL) during gas/liquid counter-current two-phase flow in a 1/30 scaled-down of Pressurized Water Reactor (PWR) hot leg geometry[J]. Nuclear Engineering and Design, 2022, 399: 112052. doi: 10.1016/j.nucengdes.2022.112052 [5] ZAPKE A, KRÖGER D G. The influence of fluid properties and inlet geometry on flooding in vertical and inclined tubes[J]. International Journal of Multiphase Flow, 1996, 22(3): 461-472. doi: 10.1016/0301-9322(95)00076-3 [6] ZAPKE A, KRÖGER D G. Countercurrent gas–liquid flow in inclined and vertical ducts-I: Flow patterns, pressure drop characteristics and flooding[J]. International Journal of Multiphase Flow, 2000, 26(9): 1439-1455. doi: 10.1016/S0301-9322(99)00097-X [7] ZAPKE A, KRÖGER D G. Countercurrent gas–liquid flow in inclined and vertical ducts-II: The validity of the Froude–Ohnesorge number correlation for flooding[J]. International Journal of Multiphase Flow, 2000, 26(9): 1457-1468. doi: 10.1016/S0301-9322(99)00098-1 [8] GHIAASIAAN S M, TURK R E, ABDEL-KHALIK S I. Countercurrent flow limitation in inclined channels with bends[J]. Nuclear Engineering and Design, 1994, 152(1-3): 379-388. doi: 10.1016/0029-5493(94)90098-1 [9] 余柳. LN2-VN2液泛过程的数值模拟及实验研究[D]. 杭州: 浙江大学,2019. [10] 陈建业. 倾斜圆管内液氮—氮蒸汽液泛流动特性及临界速度预测方法[D]. 杭州: 浙江大学,2016. [11] DEENDARLIANTO N, OUSAKA A, KARIYASAKI A, et al. Investigation of liquid film behavior at the onset of flooding during adiabatic counter-current air-water two-phase flow in an inclined pipe[J]. Nuclear Engineering and Design, 2005, 235(21): 2281-2294. doi: 10.1016/j.nucengdes.2005.03.006 [12] OUSAKA A, DEENDARLIANTO N, KARIYASAKI A, et al. Prediction of flooding gas velocity in gas–liquid counter-current two-phase flow in inclined pipes[J]. Nuclear Engineering and Design, 2006, 236(12): 1282-1292. doi: 10.1016/j.nucengdes.2005.12.001 [13] MOUZA A A, PARAS S V, KARABELAS A J. Incipient flooding in inclined tubes of small diameter[J]. International Journal of Multiphase Flow, 2003, 29(9): 1395-1412. doi: 10.1016/S0301-9322(03)00124-1 [14] MA Y F, SHAO J, LYU J, et al. Experimental study on the effect of diameter on gas–liquid CCFL characteristics of horizontal circular pipes[J]. Nuclear Engineering and Design, 2020, 364: 110645. doi: 10.1016/j.nucengdes.2020.110645 [15] 马有福,邵杰,陆鹏,等. 垂直管内气液两相逆流极限管径效应实验[J]. 核动力工程,2021, 42(1): 28-34. [16] ASTYANTO A H, NUGROHO A N A, INDARTO N, et al. Statistical characterization of the interfacial behavior captured by a novel image processing algorithm during the gas/liquid counter-current two-phase flow in a 1/3 scaled down of PWR hot leg[J]. Nuclear Engineering and Design, 2023, 404: 112179. doi: 10.1016/j.nucengdes.2023.112179 [17] WALLIS G B. One-dimensional two-phase flow[M]. New York: McGraw-Hill, 1969: 336-345. [18] PUSHKINA O L, SOROKIN Y L. Breakdown of liquid film motion in vertical tubes[J]. Heat Transfer Soviet Research, 1969, 1(5): 56-64. [19] CHEN J Y, XU L, XIONG W, et al. Experimental results of flooding experiments in an inclined tube with liquid nitrogen and its vapor[J]. Cryogenics, 2014, 62: 1-6. doi: 10.1016/j.cryogenics.2014.03.008 [20] LEE S C, BANKOFF S G. Stability of steam-water countercurrent flow in an inclined channel: Flooding[J]. Journal of Heat Transfer, 1983, 105(4): 713-718. doi: 10.1115/1.3245653 -
计量
- 文章访问数: 85
- HTML全文浏览量: 16
- PDF下载量: 42
- 被引次数: 0
