Design and Verification of OTSG Steam Pressure Linear Active Disturbance Rejection Cascade Control for Floating Nuclear Power Plant
-
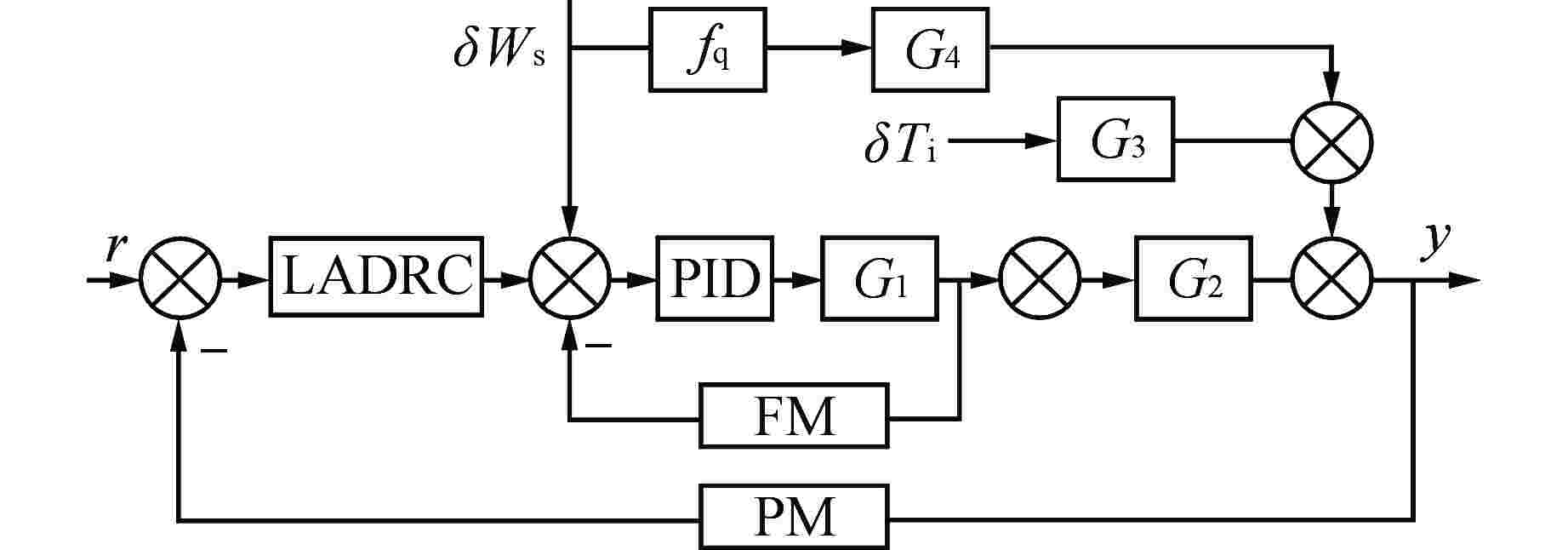
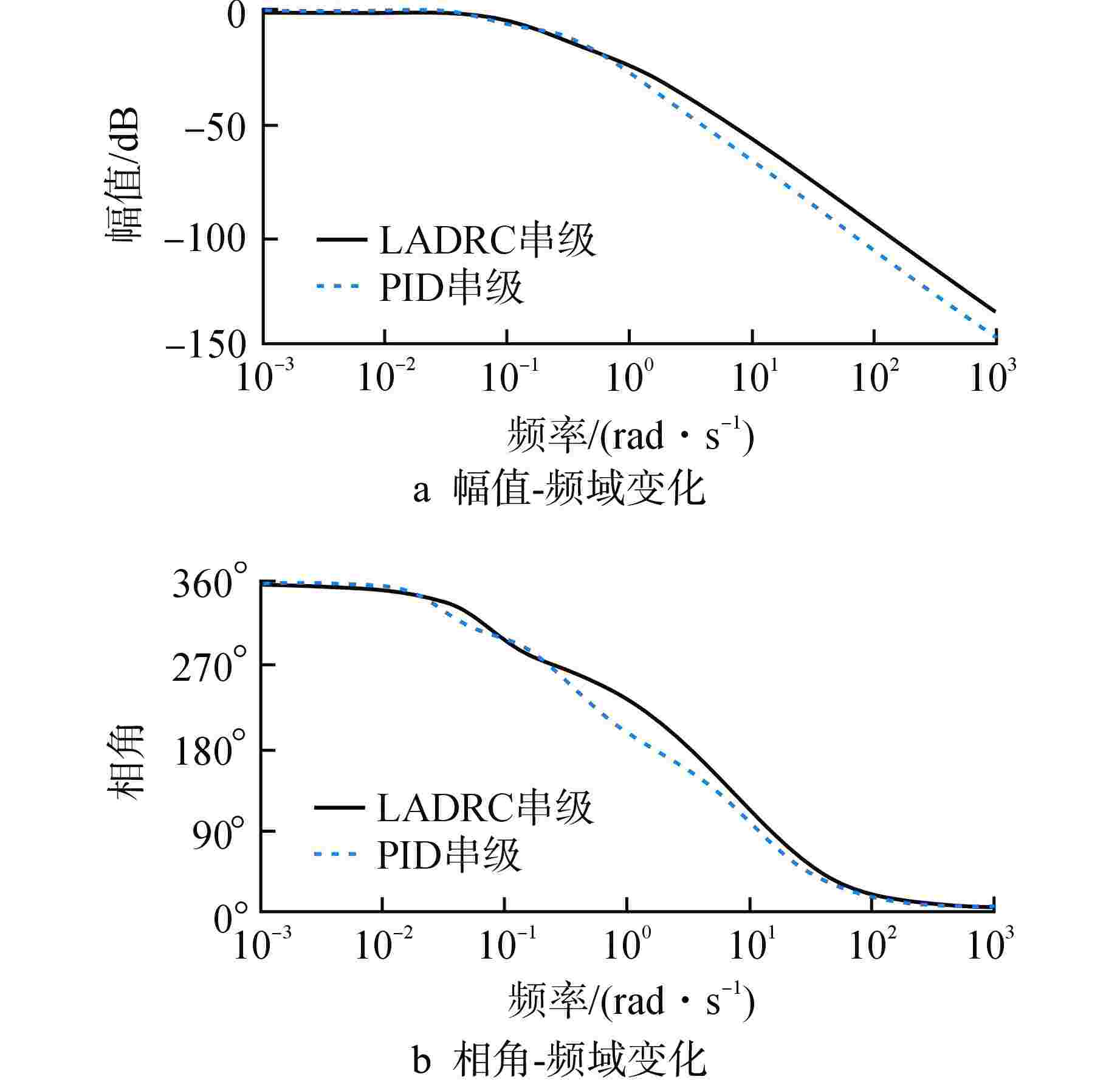
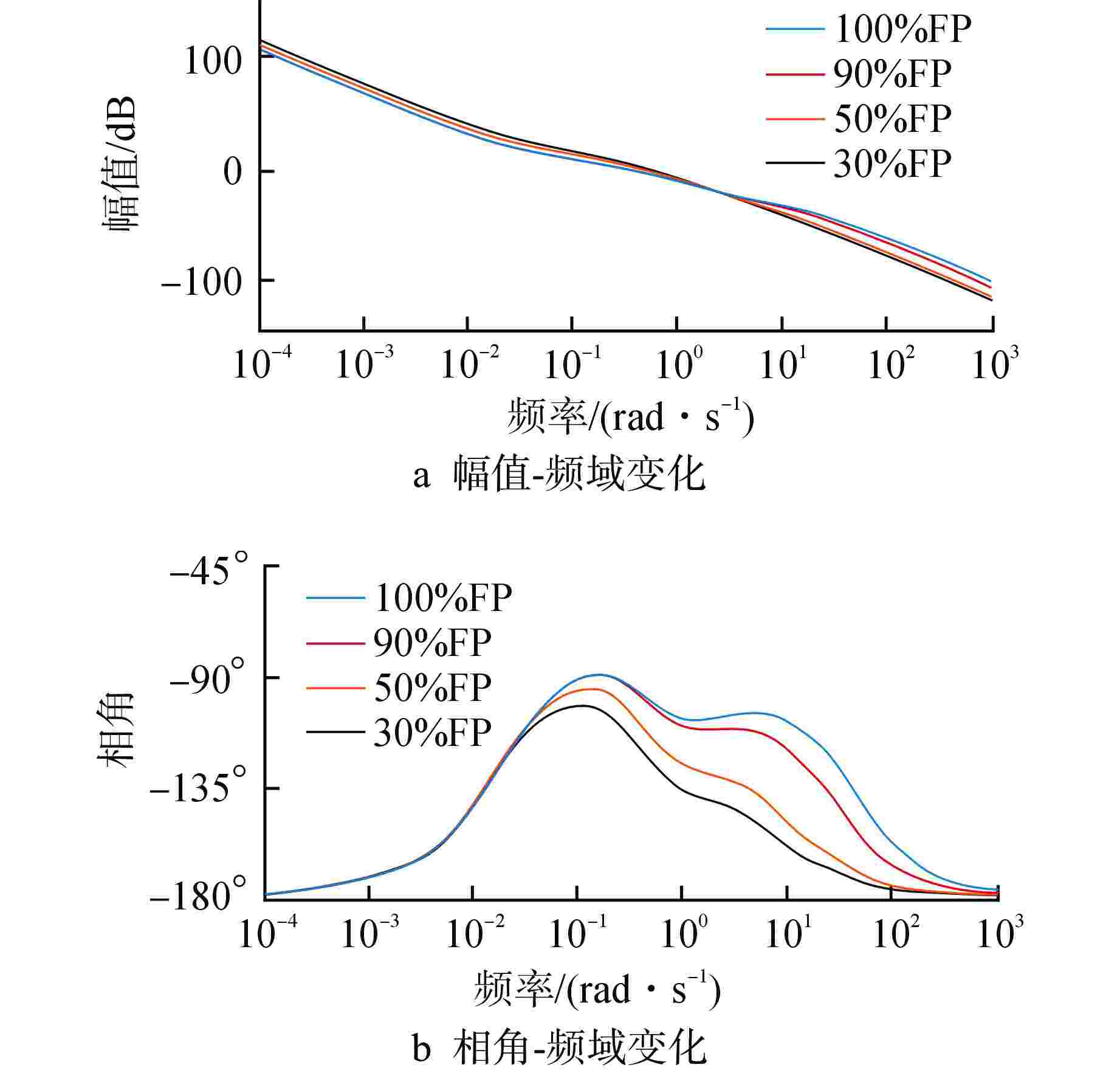
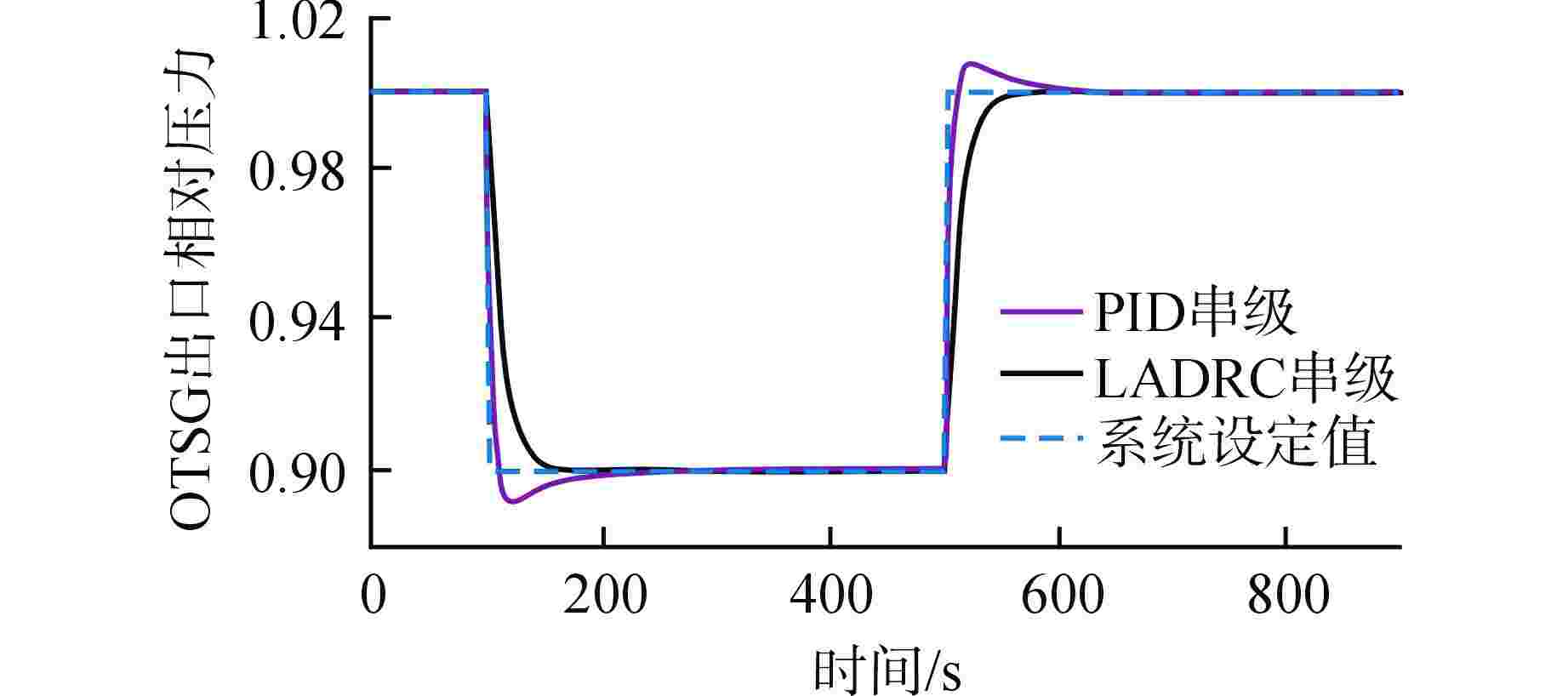
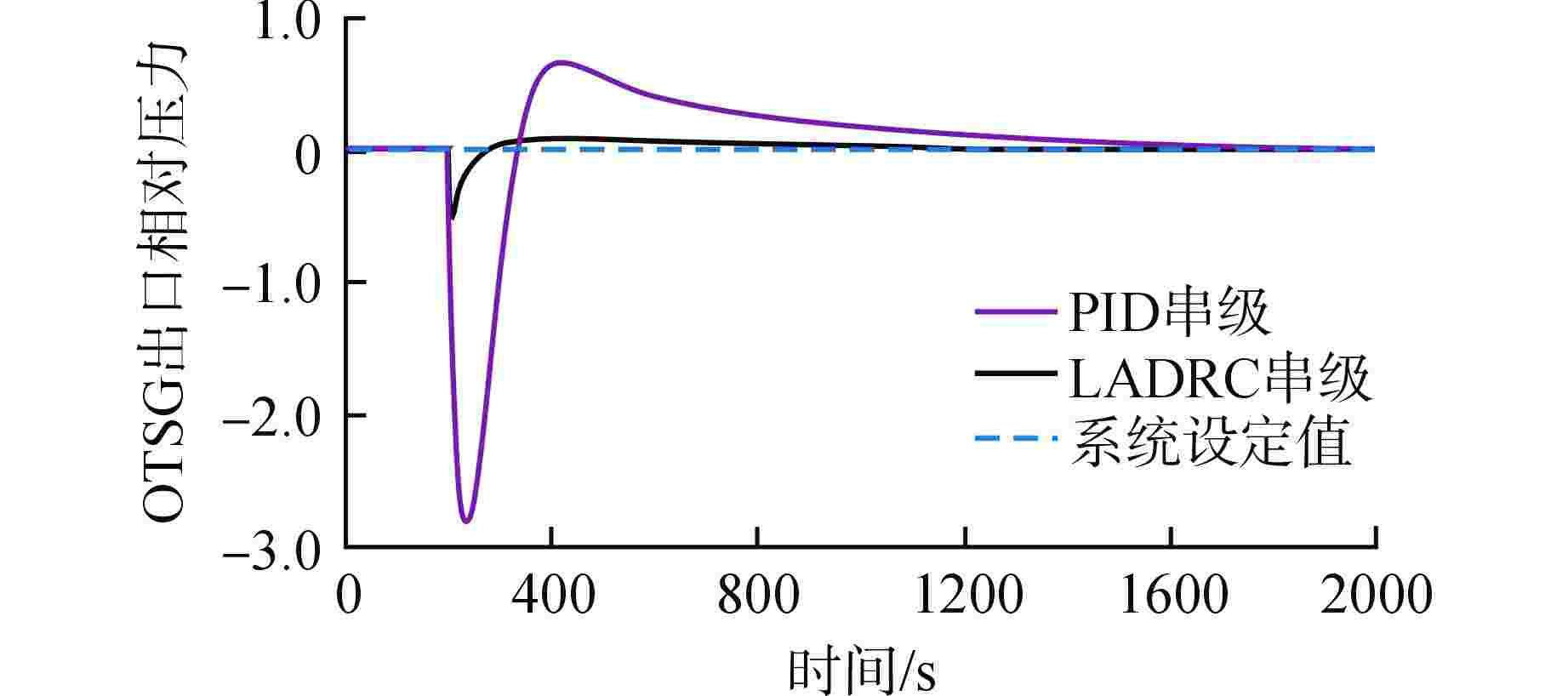
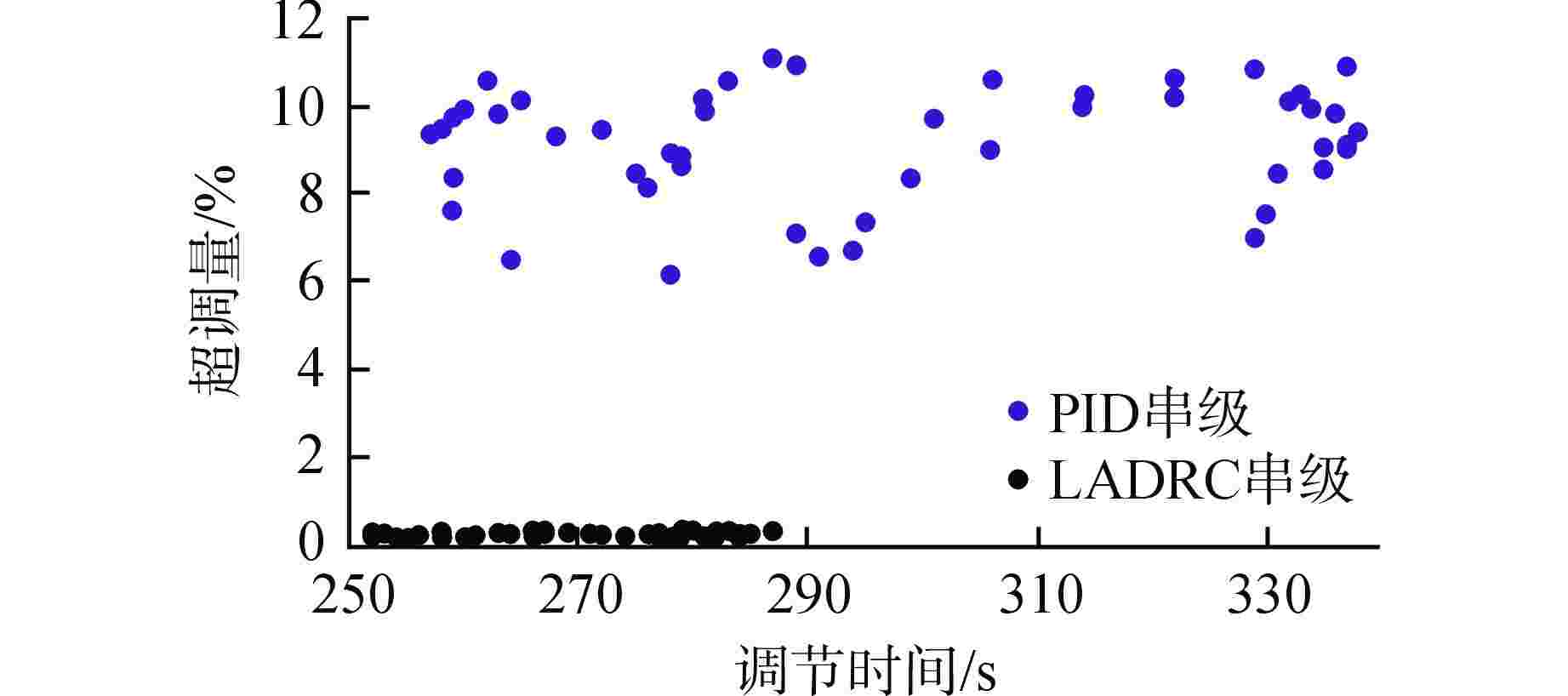
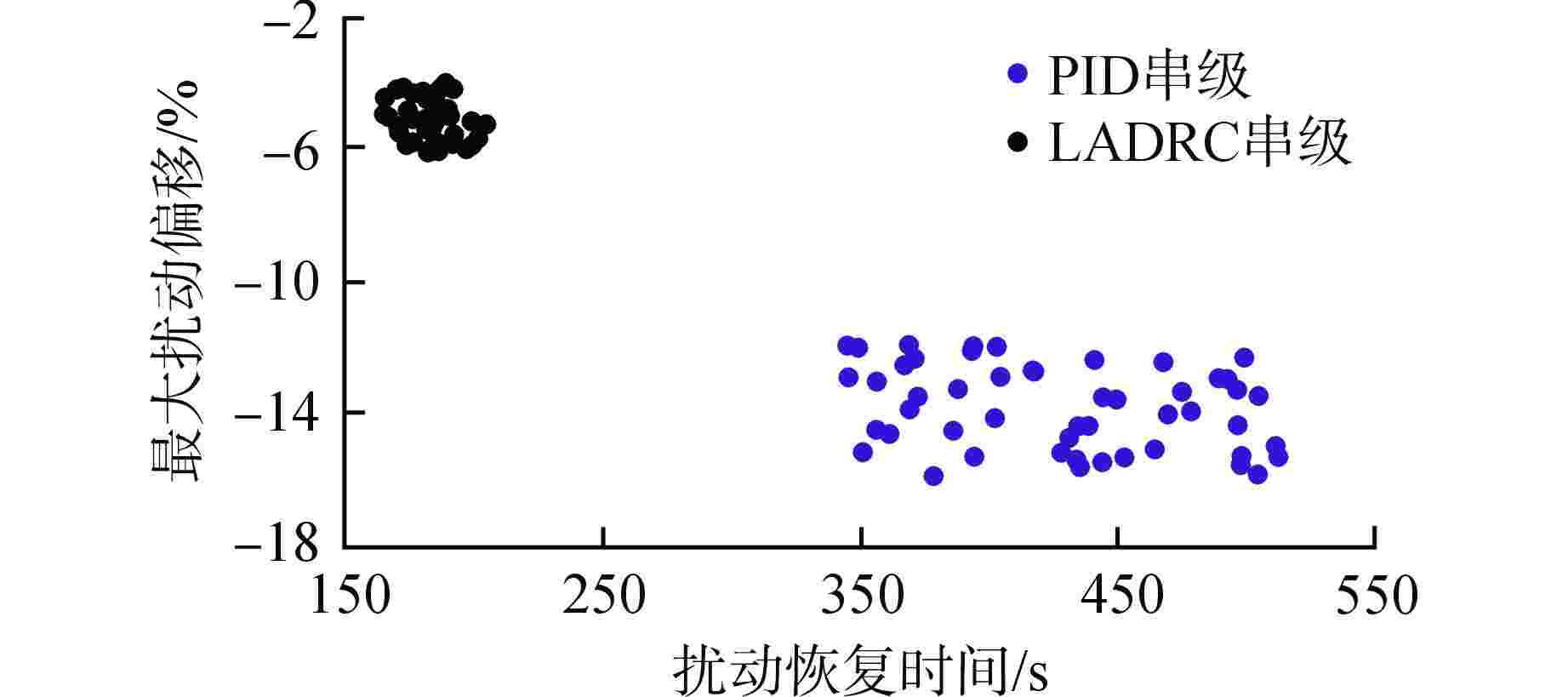
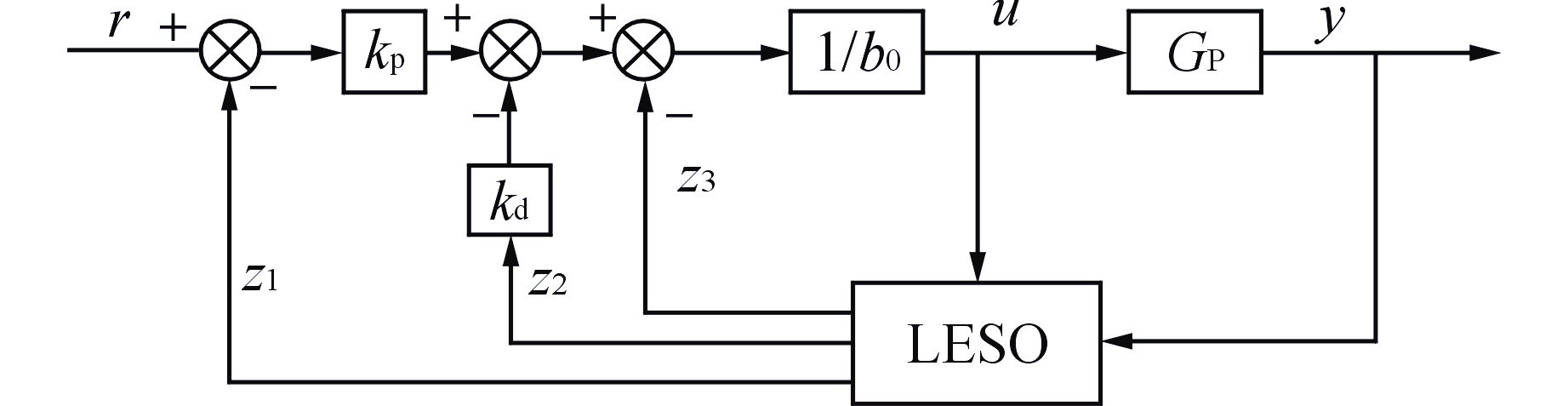
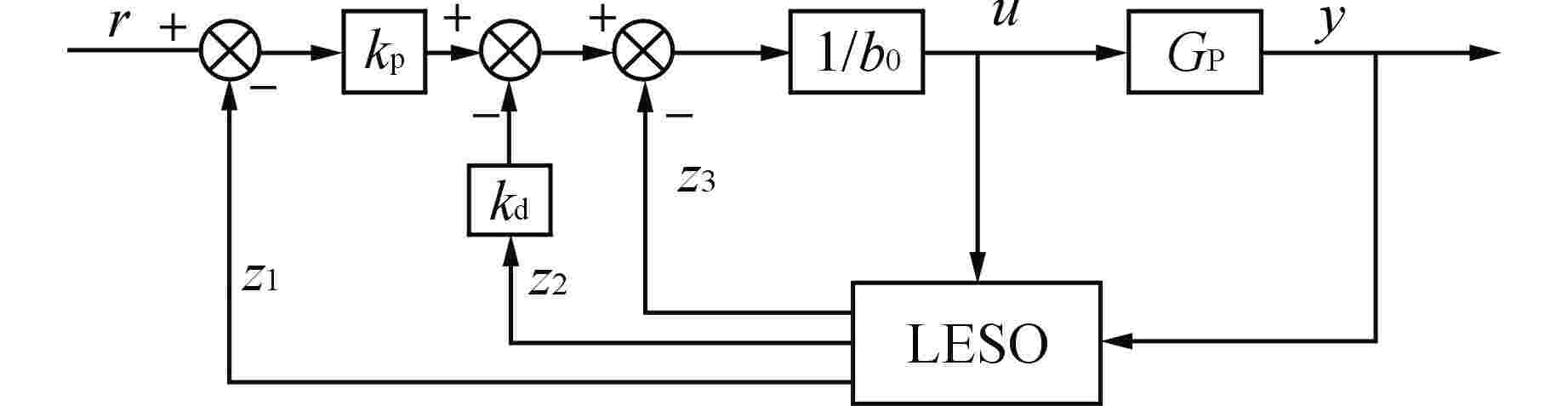
摘要: 浮动核电站的直流蒸汽发生器（OTSG）汽水容积和蓄热量较小，在存在外部扰动及负荷变化时，蒸汽压力波动较大，基于局部模型建立的单一工况水平下的比例-积分-微分（PID）控制器难以实现全工况范围内的良好控制。为此，基于系统辨识方法得到OTSG在不同工况下的传递函数模型，采用梯形隶属度函数进行加权，建立适用于OTSG蒸汽压力控制的全工况模糊模型，并将线性自抗扰控制器（LADRC）应用于OTSG的外回路，设计LADRC串级控制系统。结合频域分析方法给出OTSG稳态运行和变工况运行的LADRC工程参数调整规律，在此基础上进行参数整定，并与PID串级控制系统进行性能对比。仿真结果表明，相比PID串级控制，LADRC串级控制的响应速度更快、控制误差更小、抗干扰性和鲁棒性更强。
-
关键词:
- 浮动核电站 /
- 直流蒸汽发生器（OTSG） /
- 频域分析 /
- 线性自抗扰控制器（LADRC）
Abstract: The once-through steam generator (OTSG) of floating nuclear power plant has a small steam-water volume and heat storage capacity, and the steam pressure fluctuates greatly when there are external disturbances and load changes, so it is difficult for the PID controller based on the local model to achieve good control in the whole operating range. Therefore, based on the system identification method, the transfer function models of OTSG under different operating conditions are obtained. The trapezoidal membership function is used for weighting, and a fuzzy model under all operating conditions suitable for OTSG steam pressure control is established. The linear active disturbance rejection controller (LADRC) is applied to the outer loop of OTSG to form a cascade control system. Combined with frequency domain analysis method, the LADRC engineering parameter adjustment law of OTSG steady-state operation and variable-condition operation is given, and the parameters are adjusted on this basis, and the performance is compared with PID cascade control system. The simulation results show that compared with PID cascade control, LADRC cascade control has faster response speed, smaller control error, stronger anti-interference and robustness.-
Key words:
- Floating nuclear power plant /
- OTSG /
- Frequency domain analysis /
- LADRC
-
图 1 二阶线性自抗扰控制系统结构图
r—系统设定值；y—系统输出值；u—控制量；z1—y的估计值；z2—y微分的估计值；z3—系统扰动的估计值；b0—高频增益；LESO—线性扩张状态观测器；GP—广义被控对象；kp—线性反馈比例系数；kd—为线性反馈微分系数
Figure 1. Second Order Linear Active Disturbance Rejection Control Structure Diagram
图 2 LADRC串级控制系统结构
δTi—一次侧进口温度扰动量；PM—压力测量反馈；FM—流量测量反馈；fq—阀门全开时的蒸汽流量与满负荷时的蒸汽流量修正系数；G1—阀门开度与二次侧进口相对给水流量的传递函数；G2—二次侧进口相对给水流量与二次侧蒸汽压力的传递函数；G3—一次侧进口温度与二次侧蒸汽压力的传递函数；G4—相对蒸汽流量与二次侧蒸汽压力的传递函数
Figure 2. Structure of LADRC Cascade Control System
图 5 不同参数下LADRC串级控制性能时域对比
Figure 5. Time Domain Comparison of LADRC Control Performance with Different Parameters
图 6 100%FP负荷稳态工况下的闭环伯德图对比
Figure 6. Closed-loop Bode Diagram Comparison under 100%FP Load Steady-state Condition
图 8 相对压力阶跃下降10%的时域响应结果对比
Figure 8. Comparison of Time Domain Response Results of Relative Pressure 10% Step Drop
图 9 相对蒸汽流量10%阶跃扰动的响应结果对比
Figure 9. Comparison of Response Results of 10% Step Disturbance of Relative Steam Flow
图 10 设定值跟踪下的蒙特卡洛实验结果对比
Figure 10. Comparison of Monte Carlo Experiment Results under Set Value Tracking
图 11 扰动作用下的蒙特卡洛实验结果对比
Figure 11. Comparison of Monte Carlo Experiment Results under Perturbation
表 1 典型工况下OTSG传递函数模型
Table 1. OTSG Transfer Function Model under Typical Conditions
负荷/
%FPOTSG系统传递函数模型 G2 G3 G4 100 $ \dfrac{{0.14s + 0.16}}{{{s^2} + 31.06s}}{{\text{e}}^{ - 1.1s}} $ $ \dfrac{{0.02s + 0.005}}{{{s^2} + 0.54s + 0.065}}{{\text{e}}^{ - 0.8s}} $ $ - \dfrac{{0.051s + 0.0051}}{{{s^2} + 1.23s}}{{\text{e}}^{ - 0.6s}} $ 90 $ \dfrac{{0.08s + 0.06}}{{{s^2} + 14.47s}}{{\text{e}}^{ - 1.1s}} $ $ \dfrac{{0.018s + 0.002}}{{{s^2} + 0.35s + 0.023}}{{\text{e}}^{ - 0.8s}} $ $ - \dfrac{{0.048s + 0.0044}}{{{s^2} + 1.01s}}{{\text{e}}^{ - 0.6s}} $ 50 $ \dfrac{{0.03s + 0.03}}{{{s^2} + 4.57s}}{{\text{e}}^{ - 1.0s}} $ $ \dfrac{{0.0002s + 0.14}}{{{s^2} + 10.07s + 2.031}}{{\text{e}}^{ - 0.8s}} $ $ - \dfrac{{0.045s + 0.0037}}{{{s^2} + 0.53s}}{{\text{e}}^{ - 0.6s}} $ 30 $ \dfrac{{0.01s + 0.006}}{{{s^2} + 0.17s}}{{\text{e}}^{ - 0.9s}} $ $ \dfrac{{0.0072s + 0.022}}{{{s^2} + 2.03s + 0.326}}{{\text{e}}^{ - 0.8s}} $ $ - \dfrac{{0.044s + 0.0038}}{{{s^2} + 0.34s}}{{\text{e}}^{ - 0.5s}} $ 
下载: 导出CSV
-
[1] 许余,皇甫泽玉,胥建群,等. 直流蒸汽发生器建模与仿真研究[J]. 核动力工程,2021, 42(1): 154-160. [2] QIAN H, ZOU M Y. Design of digital nuclear power small reactor once-through steam generator control system[J]. Nuclear Engineering and Technology, 2022, 54(7): 2435-2443. doi: 10.1016/j.net.2022.01.015 [3] LI C, YU R, YU W M, et al. Pressure control of Once-through steam generator using Proximal policy optimization algorithm[J]. Annals of Nuclear Energy, 2022, 175: 109232. doi: 10.1016/j.anucene.2022.109232 [4] 成守宇,李程,彭敏俊,等. 基于人工免疫的直流蒸汽发生器压力控制研究[J]. 核动力工程,2015, 36(3): 62-65. [5] LI C, YU R, YU W M, et al. Fault-tolerant control system for once-through steam generator based on reinforcement learning algorithm[J]. Nuclear Engineering and Technology, 2022, 54(9): 3283-3292. [6] WU S F, LI Z H, WANG P F, et al. A three-region movable-boundary helical coil once-through steam generator model for dynamic simulation and controller design[J]. Nuclear Engineering and Technology, 2023, 55(2): 460-474. doi: 10.1016/j.net.2022.10.005 [7] 祁鹏展. Levy系统传递函数辨识算法的硬件实现[D]. 南京: 南京大学,2018. [8] 曾文杰,姜庆丰,谢金森,等. 基于模糊多模型的堆芯功率控制[J]. 原子能科学技术,2020, 54(3): 464-469. doi: 10.7538/yzk.2019.youxian.0254 [9] 韩京清. 自抗扰控制器及其应用[J]. 控制与决策,1998, 13(1): 19-23. doi: 10.3321/j.issn:1001-0920.1998.01.005 [10] 黄宇,张伟婷,金秀章,等. SCR脱硝系统的线性自抗扰串级控制研究[J]. 中国电机工程学报,2018, 38(18): 5518-5526. [11] SONG J, SU J C, HU Y L, et al. Stability and performance comparison analysis for linear active disturbance rejection control–based system[J]. Transactions of the Institute of Measurement and Control, 2022, 44(10): 2037-2048. doi: 10.1177/01423312211065918 [12] WAN J S, XIE J Y, WANG P F, et al. Control system design for the once-through steam generator of lead–bismuth cooled reactor based on classical control theory[J]. Annals of Nuclear Energy, 2022, 175: 109214. [13] MIYANI P B, SANT A V. Bode diagram based control system design of three phase grid tied photovoltaic systems with Quasi-Z source inverter[J]. Materials Today: Proceedings, 2022, 62: 7248-7254. [14] ZHANG Q B, GAN D Q, HUANG W, et al. Power system small-disturbance stability analysis and control design: a characteristic locus method[J]. International Journal of Electrical Power & Energy Systems, 2023, 148: 108998. -
计量
- 文章访问数: 99
- HTML全文浏览量: 24
- PDF下载量: 61
- 被引次数: 0
