基于Monte Carlo方法的两相流动参数探测不确定性研究

刘丽; 朱隆祥; 张卢腾; 马在勇; 孙皖; 潘良明; 邓坚

doi:10.13832/j.jnpe.2024.04.0038

基于Monte Carlo方法的两相流动参数探测不确定性研究

doi: 10.13832/j.jnpe.2024.04.0038

刘丽^{1, 2,},
朱隆祥^{1, 2, 3, ,},
张卢腾^{1, 2},
马在勇^{1, 2},
孙皖^{1, 2},
潘良明^{1, 2},
邓坚⁴

1.
重庆大学低品位能源利用技术及系统教育部重点实验室，重庆，400044
2.
重庆大学动力工程及工程热物理博士后科研流动站，重庆，400044
3.
重庆大学核工程与核技术系，重庆，400044
4.
中国核动力研究设计院，成都，610213

基金项目: 国家自然科学基金（U2067210，12205031）；低品位能源利用技术及系统教育部重点实验室基金（LLEUTS-2024002）

详细信息

作者简介:
刘　丽（1999—），女，硕士研究生，现从事动力工程及工程热物理方面的研究，E-mail: lllht@cqu.edu.cn

通讯作者:
朱隆祥，E-mail: lxzhu@cqu.edu.cn

中图分类号: TL334
计量
- 文章访问数: 43
- HTML全文浏览量: 9
- PDF下载量: 14
- 被引次数: 0
出版历程
- 收稿日期: 2023-10-17
- 修回日期: 2024-06-07
- 刊出日期: 2024-08-12

Study on Uncertainty of Two-Phase Flow Parameter Detection Based on Monte Carlo Method

Liu Li^{1, 2
,},
Zhu Longxiang^{1, 2, 3
, ,},
Zhang Luteng^{1, 2},
Ma Zaiyong^{1, 2},
Sun Wan^{1, 2},
Pan Liangming^{1, 2},
Deng Jian⁴

1.
Key Laboratory of Low-grade Energy Utilization Technologies and Systems, Ministry of Education, Chongqing University, Chongqing, 400044, China
2.
Postdoctoral Station of Power Engineering and Engineering Thermophysics, Chongqing University, Chongqing, 400044, China
3.
Department of Nuclear Engineering and Technology, Chongqing University, Chongqing, 400044, China
4.
Nuclear Power Institute of China, Chengdu, 610213, China

摘要

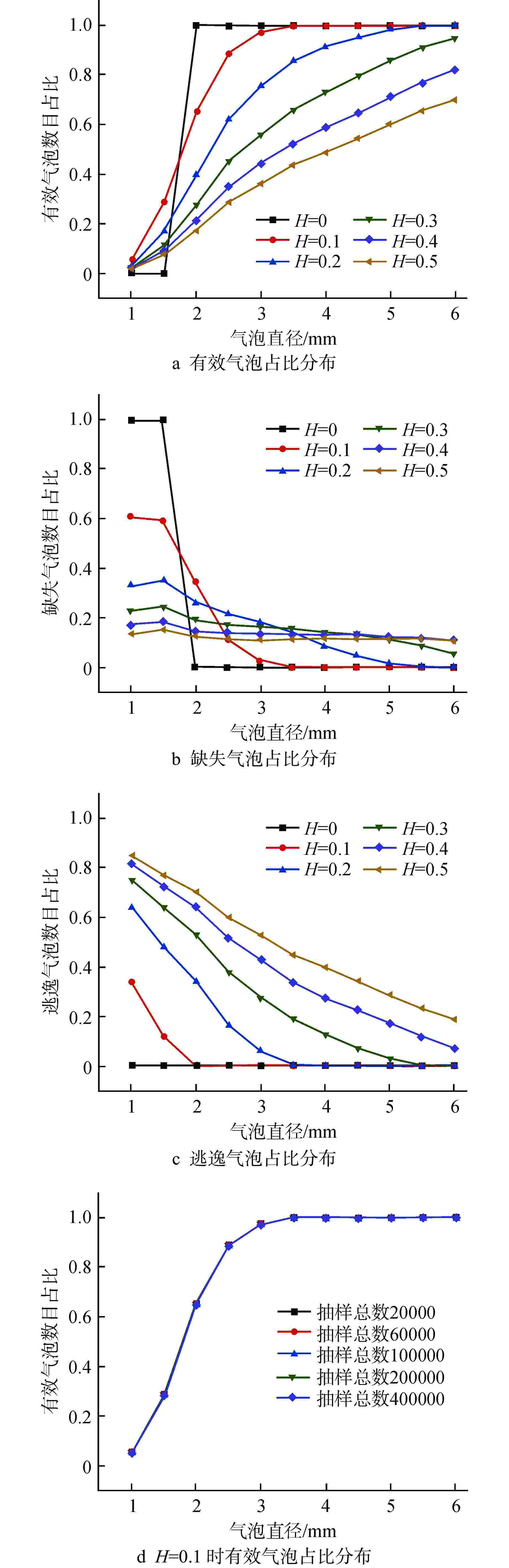
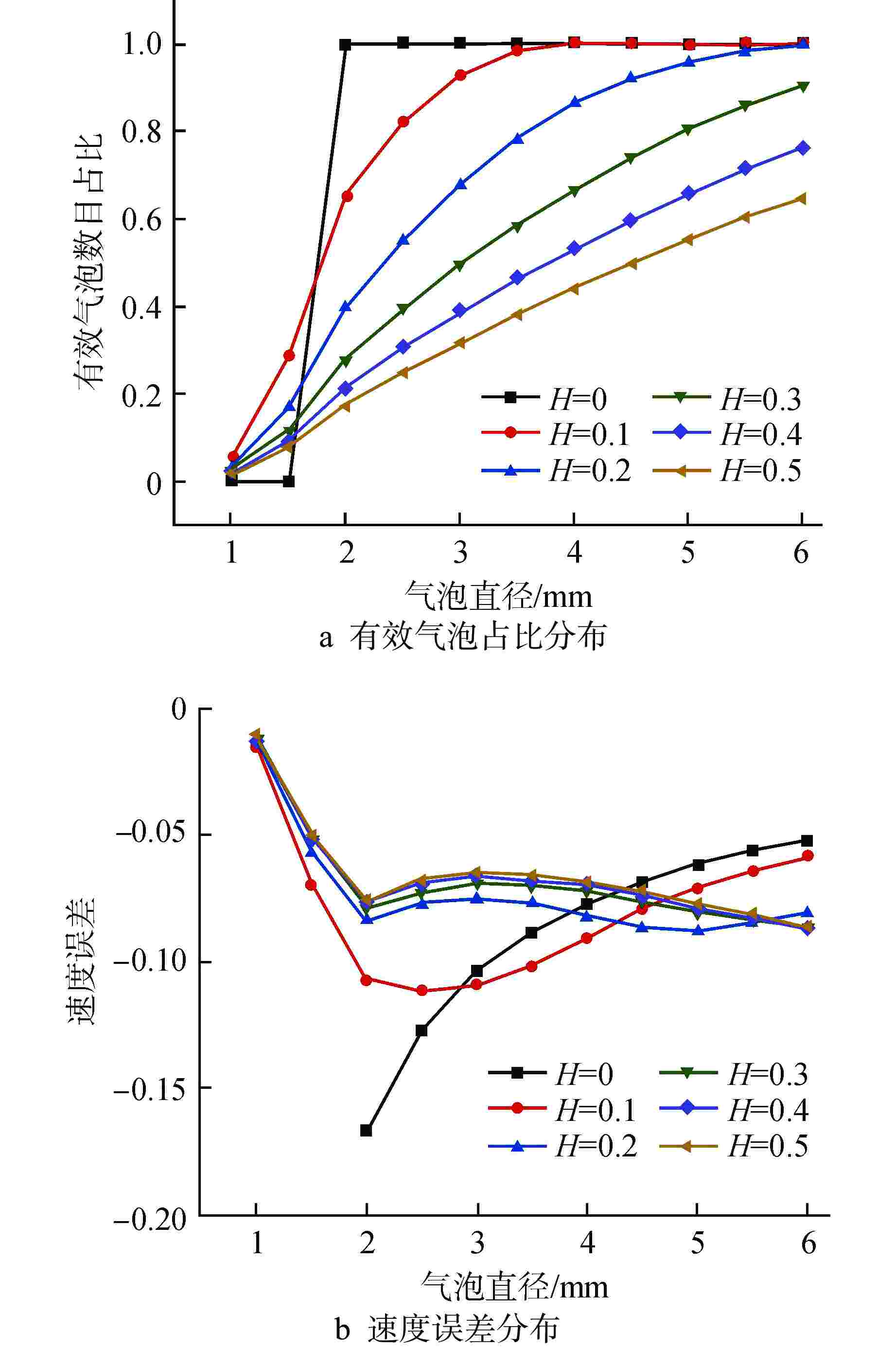
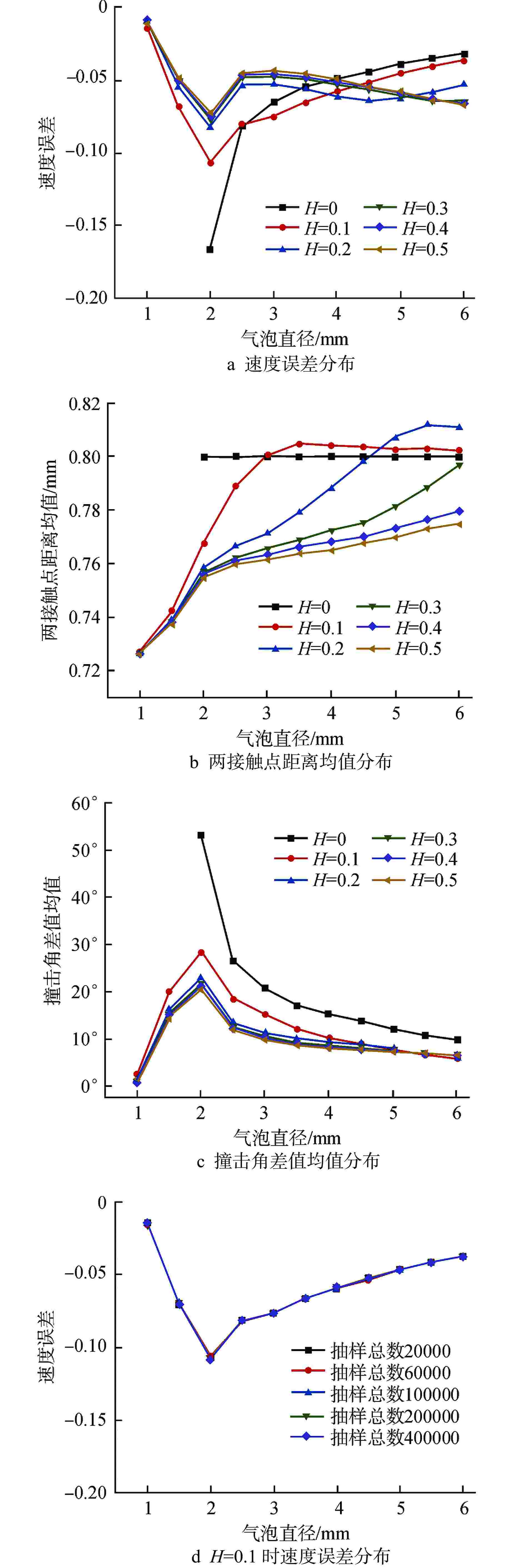
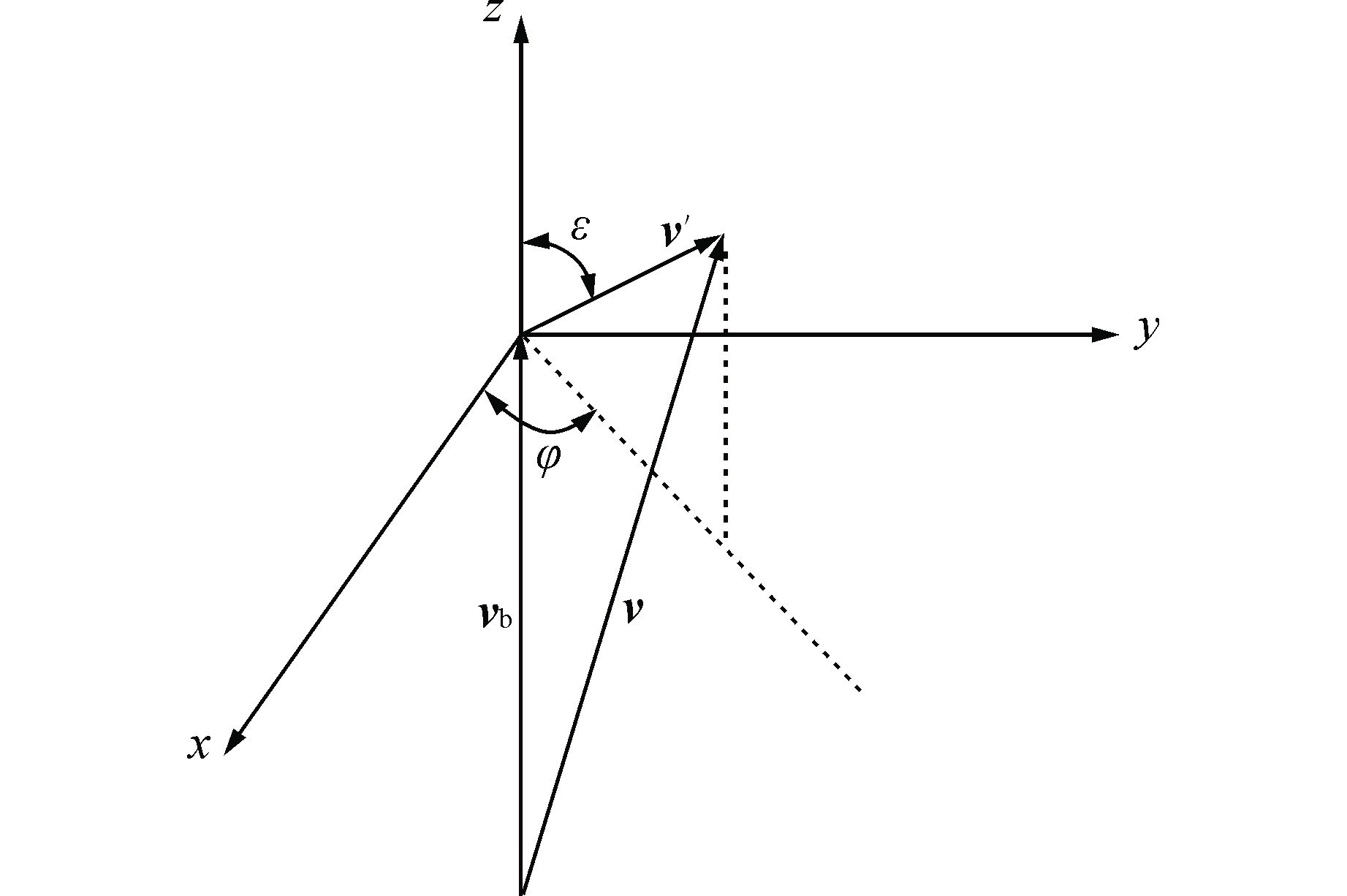
摘要: 气泡速度和气泡数目是计算界面面积浓度等相态特性的关键参数，因此对电导探针测得的气泡速度和数目进行不确定性研究是很有必要的。采用Monte Carlo方法生成大量随机气泡运动样本，得到探针捕获直径1~6 mm气泡的统计规律。通过引入相对速度波动分量H研究了气泡横向速度对有效气泡数目和气泡速度的影响。结果表明，气泡横向速度的存在可缓解由于探针横向间距而无法测量较小气泡的情况；但有效气泡数目随着气泡横向速度的增大显著降低，逃逸气泡数目增加。同时，H=0时，速度误差仅来源于探针横向间距，且速度误差随着气泡直径的增加而减小；H≠0时，对于直径大于3 mm的气泡，气泡向左或向右的横向运动反而使得探针从远离中轴线处穿过气泡，导致气泡实际移动距离增大，速度误差也增大。本文研究可为确定及修正界面面积浓度等两相流动参数不确定度提供参考。
- Monte Carlo方法 /
- 气泡横向速度 /
- 有效气泡数目 /
- 撞击角
Abstract: Bubble velocity and bubble number are key parameters for calculating the phase characteristics such as interfacial area concentration, so it is necessary to study the uncertainty of bubble velocity and number measured by the conductivity probe. The Monte Carlo method is adopted to generate a large number of random bubble motion samples, and the statistical law of1~6 mm bubbles captured by the probe is obtained. By introducing the relative velocity fluctuation component H, the influence of bubble transverse velocity on the effective bubble number and bubble velocity is studied. The results show that the presence of bubble transverse velocity alleviates the inability to measure smaller bubbles due to the probe transverse spacing. However, the number of effective bubbles significantly decreases and the number of escaping bubbles increases with the increase of bubble transverse velocity. Meanwhile, the velocity error only comes from the probe transverse spacing when H=0, and the velocity error decreases with the increase of the bubble diameter. When H≠0, for bubbles with a diameter greater than 3 mm, the transverse movement of the bubbles to the left or right makes the probe pass through the bubbles far from the central axis, which leads to the increase of the actual moving distance of the bubbles and the increase of the velocity error. This study can provide a reference for determining and correcting the uncertainty of two-phase flow parameters such as interfacial area concentration.
- Monte Carlo method /
- Bubble transverse velocity /
- Effective bubble number /
- Hitting angle

HTML全文

图 1 气泡速度矢量示意图

Figure 1. Schematic Diagram of Bubble Velocity Vector

下载: 全尺寸图片幻灯片

图 2 有效气泡信号和3类无效气泡信号

s₀—0#探针采集的电压信号；s₁—1#探针采集的电压信号

Figure 2. Effective Bubble Signal and Three Kinds of Invalid Bubble Signals

下载: 全尺寸图片幻灯片

图 3 各直径有效、缺失、逃逸气泡数目占比分布

Figure 3. Distribution of Effective, Missing and Escaping Bubble Ratios by Diameter

下载: 全尺寸图片幻灯片

图 4 气泡形状全为球形时的有效气泡数目占比和速度误差分布

Figure 4. Distribution of Effective Bubble Ratio and Velocity Error under All Spherical Bubbles

下载: 全尺寸图片幻灯片

图 5 不同H下各直径气泡参数分布

Figure 5. Parameter Distribution of Bubbles by Diameter for Different H

下载: 全尺寸图片幻灯片

参考文献(15)

[1]	KATAOKA I, ISHII M, SERIZAWA A. Local formulation and measurements of interfacial area concentration in two-phase flow[J]. International Journal of Multiphase Flow, 1986, 12(4): 505-529. doi: 10.1016/0301-9322(86)90057-1
[2]	REVANKAR S T, ISHII M. Local interfacial area measurement in bubbly flow[J]. International Journal of Heat and Mass Transfer, 1992, 35(4): 913-925. doi: 10.1016/0017-9310(92)90257-S
[3]	LEUNG W H, REVANKAR S T, ISHII Y, et al. Axial development of interfacial area and void concentration profiles measured by double-sensor probe method[J]. International Journal of Heat and Mass Transfer, 1995, 38(3): 445-453. doi: 10.1016/0017-9310(94)00181-T
[4]	SHEN X Z, NAKAMURA H. Local interfacial velocity measurement method using a four-sensor probe[J]. International Journal of Heat and Mass Transfer, 2013, 67: 843-852. doi: 10.1016/j.ijheatmasstransfer.2013.08.064
[5]	KIM S, FU X Y, WANG X, et al. Development of the miniaturized four-sensor conductivity probe and the signal processing scheme[J]. International Journal of Heat and Mass Transfer, 2000, 43(22): 4101-4118. doi: 10.1016/S0017-9310(00)00046-6
[6]	HIBIKI T, HOGSETT S, ISHII M. Local measurement of interfacial area, interfacial velocity and liquid turbulence in two-phase flow[J]. Nuclear Engineering and Design, 1998, 184(2-3): 287-304. doi: 10.1016/S0029-5493(98)00203-9
[7]	REVANKAR S T, ISHII M. Theory and measurement of local interfacial area using a four sensor probe in two-phase flow[J]. International Journal of Heat and Mass Transfer, 1993, 36(12): 2997-3007. doi: 10.1016/0017-9310(93)90029-6
[8]	KATAOKA I, ISHII M, SERIZAWA A. Sensitivity analysis of bubble size and probe geometry on the measurements of interfacial area concentration in gas-liquid two-phase flow[J]. Nuclear Engineering and Design, 1994, 146(1-3): 53-70. doi: 10.1016/0029-5493(94)90320-4
[9]	SHEN X Z, SAITO Y, MISHIMA K, et al. Methodological improvement of an intrusive four-sensor probe for the multi-dimensional two-phase flow measurement[J]. International Journal of Multiphase Flow, 2005, 31(5): 593-617. doi: 10.1016/j.ijmultiphaseflow.2005.02.003
[10]	SHEN X Z, MISHIMA K, NAKAMURA H. Error reduction, evaluation and correction for the intrusive optical four-sensor probe measurement in multi-dimensional two-phase flow[J]. International Journal of Heat and Mass Transfer, 2008, 51(3-4): 882-895. doi: 10.1016/j.ijheatmasstransfer.2006.01.054
[11]	WU Q, ISHII M. Sensitivity study on double-sensor conductivity probe for the measurement of interfacial area concentration in bubbly flow[J]. International Journal of Multiphase Flow, 1999, 25(1): 155-173. doi: 10.1016/S0301-9322(98)00037-8
[12]	WU Q, WELTER K, MCCREARY D, et al. Theoretical studies on the design criteria of double-sensor probe for the measurement of bubble velocity[J]. Flow Measurement and Instrumentation, 2001, 12(1): 43-51. doi: 10.1016/S0955-5986(00)00041-8
[13]	WANG D W, FU Y C, LIU Y, et al. A comprehensive uncertainty evaluation of double-sensor conductivity probe[J]. Progress in Nuclear Energy, 2021, 136: 103741. doi: 10.1016/j.pnucene.2021.103741
[14]	WANG D, LIU Y, TALLEY J D. Numerical evaluation of the uncertainty of double-sensor conductivity probe for bubbly flow measurement[J]. International Journal of Multiphase Flow, 2018, 107: 51-66. doi: 10.1016/j.ijmultiphaseflow.2018.05.019
[15]	LE CORRE J M, ISHII M. Numerical evaluation and correction method for multi-sensor probe measurement techniques in two-phase bubbly flow[J]. Nuclear Engineering and Design, 2002, 216(1-3): 221-238. doi: 10.1016/S0029-5493(02)00130-9