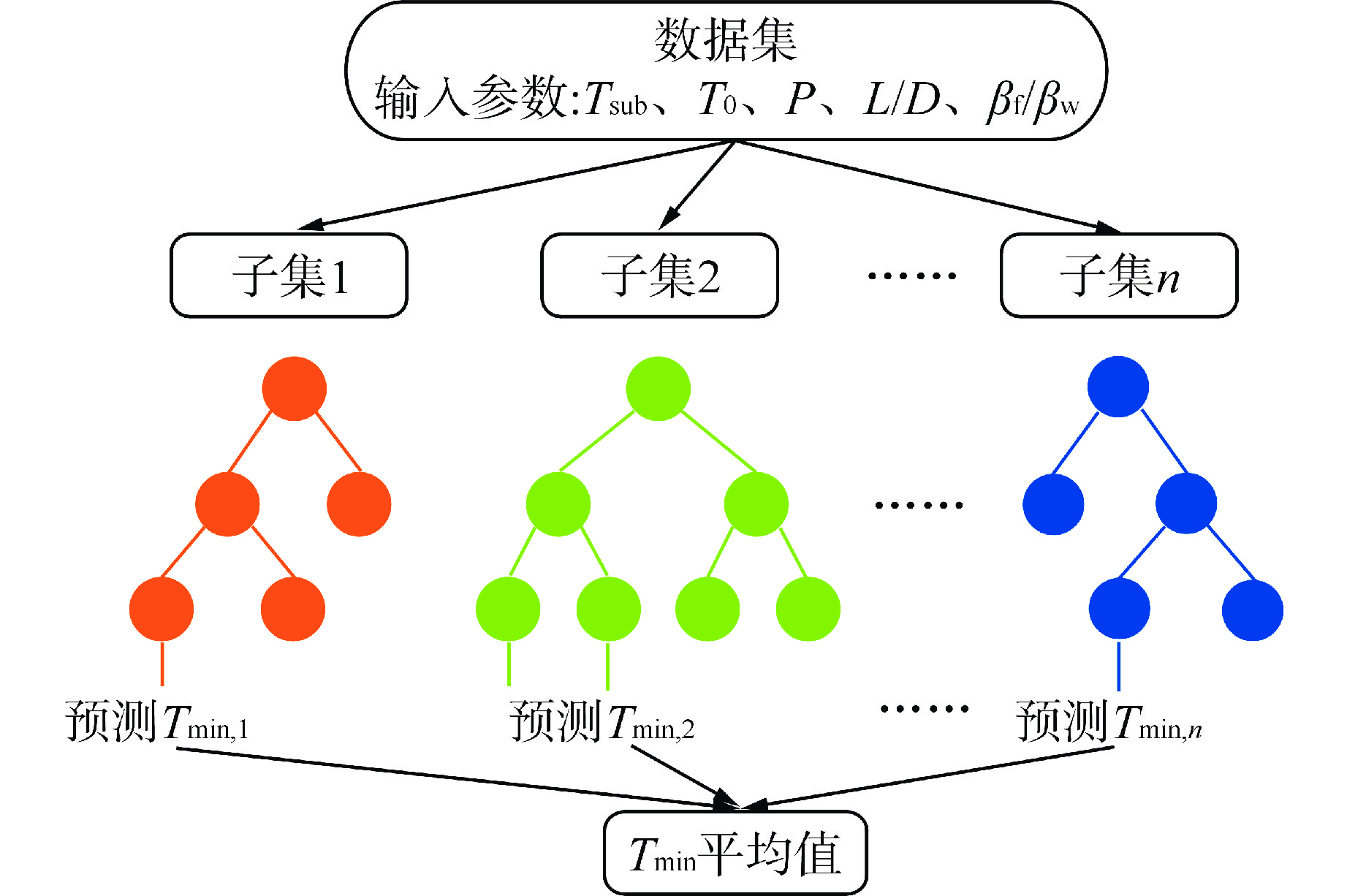
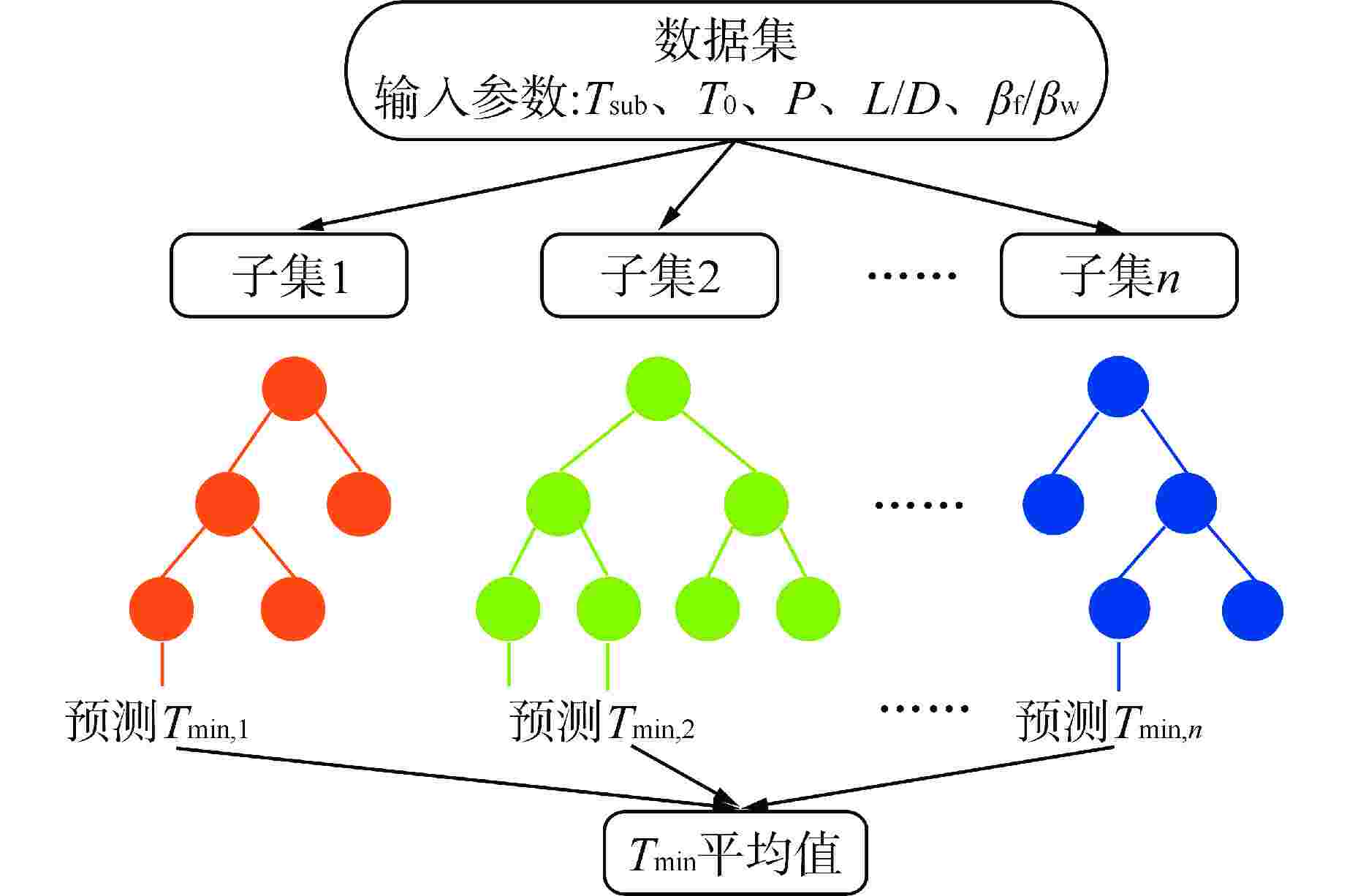
Research on Prediction and Sensitivity Analysis of Minimum Film Boiling Temperature of Quenching Boiling Based on Machine Learning
-
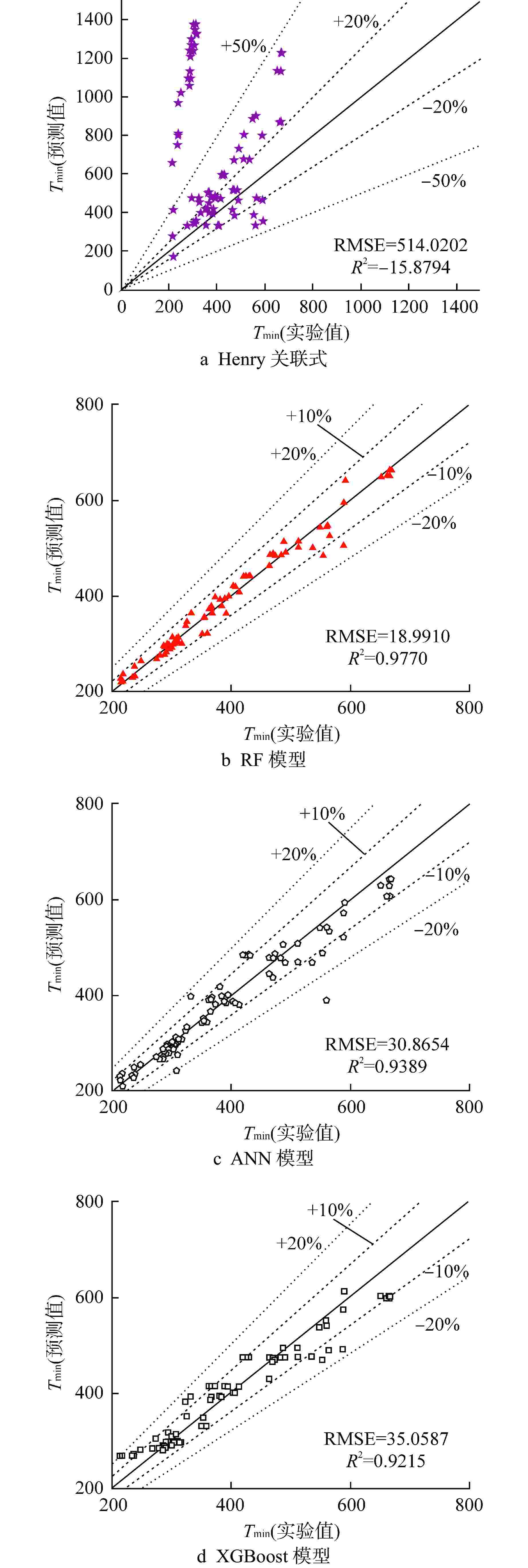
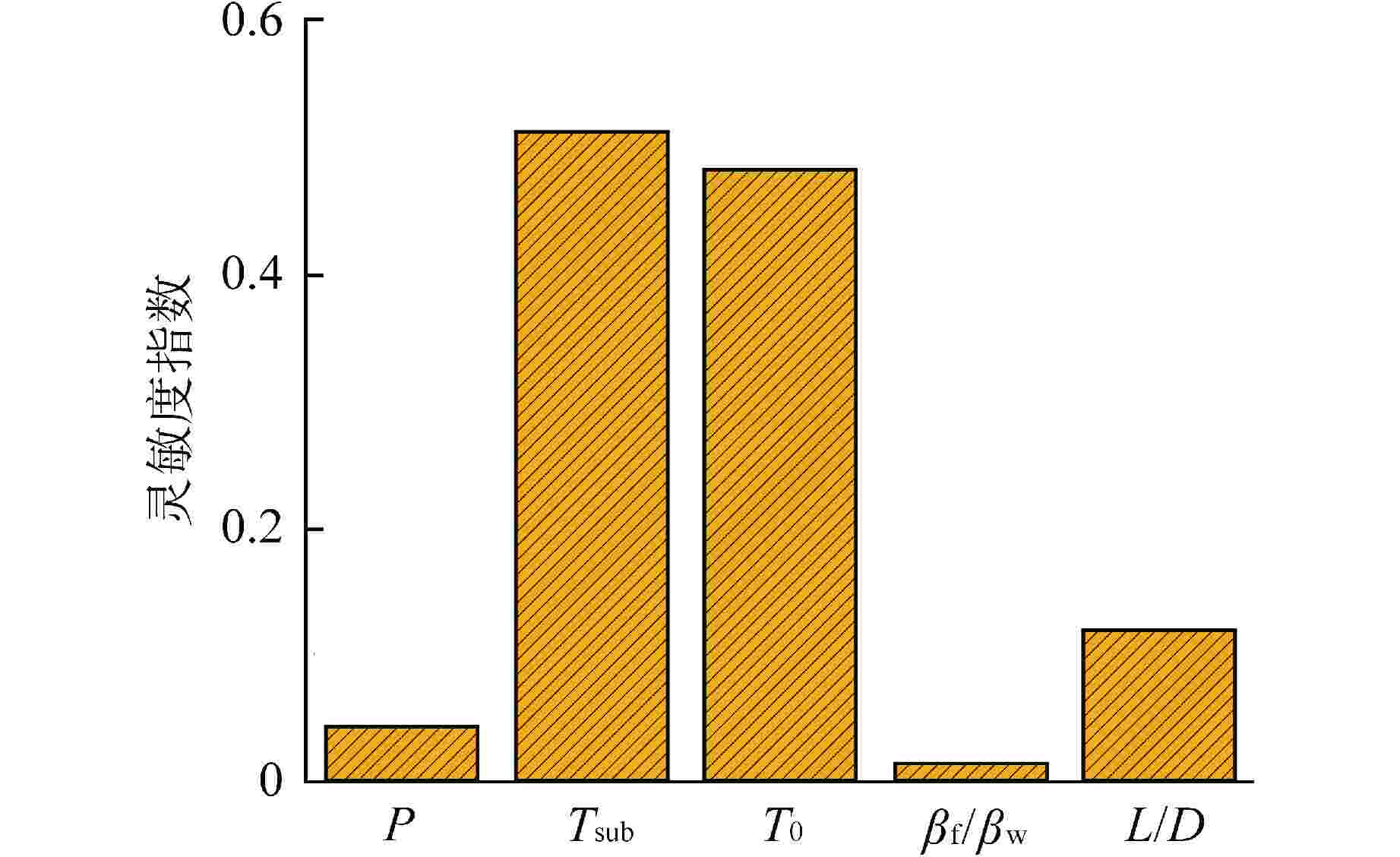
摘要: 淬冷沸腾广泛应用于核反应堆失水事故后燃料棒的冷却过程中，最小膜态沸腾温度（Tmin）的确定对核反应堆的安全运行至关重要。本文基于文献的实验数据，选用了3种典型机器学习模型：随机森林（RF）、人工神经网络（ANN）和极端梯度提升（XGBoost），对淬冷沸腾Tmin进行预测和影响因素灵敏度分析研究。结果表明，机器学习方式能够有效提高淬冷沸腾Tmin预测的准确性，其预测性能相较于传统的经验关联式有大幅提升，其中RF模型预测效果最优，决定系数R2为0.9770；通过结合RF模型和Sobol’全局灵敏度方法，得到对淬冷沸腾Tmin影响最大的参数为冷却剂过冷度，其次为初始壁温，长径比、压力、热物性对其影响较小。本文研究成果将为提高核反应堆的安全性提供理论指导。Abstract: Quenching boiling is widely used in the cooling process of fuel rods after the loss of coolant accident in nuclear reactor. The determination of the minimum film boiling temperature (Tmin) is very important for the safe operation of nuclear reactors. Based on the experimental data in the literature, this paper selects three typical machine learning models: Random Forest (RF), Artificial Neural Network (ANN) and eXtreme Gradient Boosting (XGBoost) to predict Tmin during quenching boiling and conduct a sensitivity analysis of influencing factors. The results show that the machine learning method can effectively improve the accuracy of Tmin prediction compared to the traditional empirical correlation. Among the models, the RF model exhibits the best predictive performance with a coefficient of determination R2 of 0.9770. By combining the RF model with the Sobol’ global sensitivity method, the study identifies the coolant subcooling as the most influential parameter on Tmin, followed by initial wall temperature, while length-diameter ratio, pressure and thermophysical properties have a smaller impact. The findings of this research will provide theoretical guidance for improving the safety of nuclear reactors.
-
图 4 机器学习和Henry模型预测淬冷沸腾Tmin的准确度对比
Figure 4. Comparison of Accuracy between Machine Learning and Henry Model in Predicting Tmin for Quenching Boiling
图 5 基于RF模型的淬冷沸腾Tmin影响因素全局灵敏度分析结果
Figure 5. Global Sensitivity Analysis Results of Influencing Factors of Quench Boiling Tmin Based on RF Model
表 1 文献中的Tmin数据集
Table 1. Tmin Dataset in Literature
作者 Tsub/℃ T0/℃ P/MPa L/D βf/βw 包壳材料 数据点数量 Li等[7] 0~40.0 750 0.1 5 0.057 不锈钢 5 Lee and Kim[8] 0 600 0.1 5 0.002~0.057 铜，不锈钢，锆合金 3 Yeom等[9-10] 0~30.0 650 0.1~0.623 5.1~5.15 0.115~0.531 锆合金，氧化锆 35 Ho等[11] 0~30.0 600 0.1 4.67 0.012 黄铜 2 Sakurai等[3] 0 526 0.1~2.063 16.67~41.6 0.015 铂 121 Peterson and Bajorek[12] 0~30.85 675 0.1~3.003 6.35~6.68 0.017~0.119 锆合金，碳钢，不锈钢 129 Ebrahim等[13] 2.0~20.0 450~650 0.1 26.7 0.032~0.066 锆合金，镍铁合金，不锈钢 84 Xiong等[14] 0~20.0 600 0.1 5.75 0.03 铁铬铝合金 5 Lee等[4] 0 400 0.1 6 0.002~0.057 铜，不锈钢 2 Hurley and Duarte[15] 2.0~12.0 510 0.1 31.58 0.026~0.053 镍铜合金，镍铁合金，不锈钢 11 张琪琪等[16] 5.0~20.0 620 0.1 6.5 0.057 不锈钢 4 王泽锋等[17] 5.0~20.0 600 0.1 5.75 0.102 锆合金 5 Xiong等[18] 5.0~25.0 600 0.1 6.5 0.03~0.102 锆合金，铁铬铝合金 10 
下载: 导出CSV
表 2 不同决策树数量条件下RF模型预测性能对比
Table 2. Comparison of Prediction Performance of RF Model under Different Decision Tree Numbers
决策树数量 RMSE R2 10 20.1431 0.9725 20 19.9435 0.9746 30 19.7747 0.9750 40 19.8531 0.9748 50 19.3697 0.9760 60 18.9910 0.9770 70 19.2617 0.9763 80 19.3298 0.9761 90 19.5394 0.9756 100 19.6504 0.9753
下载: 导出CSV
表 3 不同隐藏层架构条件下ANN模型预测性能对比
Table 3. Comparison of Prediction Performance of ANN Model under Different Hidden Layer Architectures
架构 RMSE R2 5-60-1 34.7980 0.9221 5-40-40-1 33.5517 0.9277 5-50-50-1 31.7392 0.9354 5-60-60-1 31.0522 0.9383 5-40-40-40-1 32.0389 0.9339 5-50-50-50-1 30.8654 0.9389 5-60-60-60-1 31.0644 0.9374
下载: 导出CSV
表 4 不同弱学习器数量条件下XGBoost模型预测性能对比
Table 4. Comparison of Prediction Performance of XGBoost Model under Different Weak Learner Numbers
弱学习器数量 RMSE R2 50 36.12307 0.9166 100 35.05868 0.9215
下载: 导出CSV
-
[1] 熊平. 圆柱骤冷沸腾表面热流密度反演及沸腾传热特性研究[D]. 北京: 北京化工大学,2021. [2] IN W K, LEE K G. Quenching experiments with CrAl-coated zircaloy cladding in reflooding water flows[J]. Energies, 2021, 14(7): 1859. doi: 10.3390/en14071859 [3] SAKURAI A, SHIOTSU M, HATA K. Effect of system pressure on film-boiling heat transfer, minimum heat flux, and minimum temperature[J]. Nuclear Science and Engineering, 1984, 88(3): 321-330. doi: 10.13182/NSE84-A18586 [4] LEE C Y, CHUN T H, IN W K. Effect of change in surface condition induced by oxidation on transient pool boiling heat transfer of vertical stainless steel and copper rodlets[J]. International Journal of Heat and Mass Transfer, 2014, 79: 397-407. doi: 10.1016/j.ijheatmasstransfer.2014.08.030 [5] ZHAO X G, SHIRVAN K, SALKO R K, et al. On the prediction of critical heat flux using a physics-informed machine learning-aided framework[J]. Applied Thermal Engineering, 2020, 164: 114540. doi: 10.1016/j.applthermaleng.2019.114540 [6] ZHANG J F, ZHONG D W, SHI H P, et al. Machine learning prediction of critical heat flux on downward facing surfaces[J]. International Journal of Heat and Mass Transfer, 2022, 191: 122857. doi: 10.1016/j.ijheatmasstransfer.2022.122857 [7] LI J Q, MOU L W, ZHANG H Y, et al. Pool boiling heat transfer and quench front velocity during quenching of a rodlet in subcooled water: effects of the degree of subcooling[J]. Experimental Heat Transfer, 2018, 31(2): 148-160. doi: 10.1080/08916152.2017.1397819 [8] LEE C Y, KIM S. Parametric investigation on transient boiling heat transfer of metal rod cooled rapidly in water pool[J]. Nuclear Engineering and Design, 2017, 313: 118-128. doi: 10.1016/j.nucengdes.2016.12.005 [9] YEOM H, JO H, JOHNSON G, et al. Transient pool boiling heat transfer of oxidized and roughened Zircaloy-4 surfaces during water quenching[J]. International Journal of Heat and Mass Transfer, 2018, 120: 435-446. doi: 10.1016/j.ijheatmasstransfer.2017.12.060 [10] YEOM H. High temperature corrosion and heat transfer studies of zirconium-silicide coatings for light water reactor cladding applications[D]. Madison: Univ. of Wisconsin-Madison, 2017. [11] HO Y H, HO M X, PAN C. The effects of subcooling on quenching of a vertical brass cylinder with heating power[C]//International Conference on Nuclear Engineering. Arlington: American Society of Mechanical Engineers, 2015, 56864: V001T04A001HO Y H, HO M X, PAN C. The effects of subcooling on quenching of a vertical brass cylinder with heating power[C]//International Conference on Nuclear Engineering. Arlington: American Society of Mechanical Engineers, 2015, 56864: V001T04A001 [12] PETERSON L J, BAJOREK S M. Experimental investigation of minimum film boiling temperature for vertical cylinders at elevated pressure[C]//10th International Conference on Nuclear Engineering. Arlington: American Society of Mechanical Engineers, 2002: 883-892. [13] EBRAHIM S A, CHANG S, CHEUNG F B, et al. Parametric investigation of film boiling heat transfer on the quenching of vertical rods in water pool[J]. Applied Thermal Engineering, 2018, 140: 139-146. doi: 10.1016/j.applthermaleng.2018.05.021 [14] XIONG J B, WANG Z F, XIONG P, et al. Experimental investigation on transient boiling heat transfer during quenching of fuel cladding surfaces[J]. International Journal of Heat and Mass Transfer, 2020, 148: 119131. doi: 10.1016/j.ijheatmasstransfer.2019.119131 [15] HURLEY P, DUARTE J P. Implementation of fiber optic temperature sensors in quenching heat transfer analysis[J]. Applied Thermal Engineering, 2021, 195: 117257. doi: 10.1016/j.applthermaleng.2021.117257 [16] 张琪琪,熊平,周佳樾,等. 不锈钢棒材形状对淬冷沸腾的影响研究[J]. 工程热物理学报,2023, 44(2): 463-467. [17] 王泽锋,邓坚,王嘉庚,等. 锆-4在冷却水中的骤冷沸腾传热实验研究[J]. 核动力工程,2021, 42(1): 186-191. [18] XIONG P, LU T, LUO Y, et al. Study on liquid–vapor interface oscillation characteristics and heat transfer of film boiling during quenching of fuel cladding surfaces[J]. Applied Thermal Engineering, 2023, 219: 119615. doi: 10.1016/j.applthermaleng.2022.119615 [19] SALTELLI A, RATTO M, TARANTOLA S, et al. Sensitivity analysis practices: strategies for model-based inference[J]. Reliability Engineering & System Safety, 2006, 91(10-11): 1109-1125. [20] SOBOL' I M. On the distribution of points in a cube and the approximate evaluation of integrals[J]. USSR Computational Mathematics and Mathematical Physics, 1967, 7(4): 784-802. [21] 杨龙,严振华,王明哲. QFD与Sobol’法在武器装备需求分析中的应用[J]. 舰船电子工程,2012, 32(3): 107-109,116. doi: 10.3969/j.issn.1627-9730.2012.03.040 [22] ZADEH F K, NOSSENT J, SARRAZIN F, et al. Comparison of variance-based and moment-independent global sensitivity analysis approaches by application to the SWAT model[J]. Environmental Modelling & Software, 2017, 91: 210-222. [23] HENRY R E. A correlation for the minimum film boiling temperature[J]. AIChE Symposium Series, 1974, 70(138): 81-90. [24] FOX E W, VER HOEF J M, OLSEN A R. Comparing spatial regression to random forests for large environmental data sets[J]. PLoS One, 2020, 15(3): e0229509. doi: 10.1371/journal.pone.0229509 [25] MEYER H, PEBESMA E. Predicting into unknown space? Estimating the area of applicability of spatial prediction models[J]. Methods in Ecology and Evolution, 2021, 12(9): 1620-1633. doi: 10.1111/2041-210X.13650 [26] TAKOUTSING B, HEUVELINK G B M. Comparing the prediction performance, uncertainty quantification and extrapolation potential of regression kriging and random forest while accounting for soil measurement errors[J]. Geoderma, 2022, 428: 116192. doi: 10.1016/j.geoderma.2022.116192 [27] MUCKLEY E S, SAAL J E, MEREDIG B, et al. Interpretable models for extrapolation in scientific machine learning[J]. Digital Discovery, 2023, 2(5): 1425-1435. doi: 10.1039/D3DD00082F [28] BOOKER D J, WHITEHEAD A L. Inside or outside: quantifying extrapolation across river networks[J]. Water Resources Research, 2018, 54(9): 6983-7003. doi: 10.1029/2018WR023378 -
图(5) / 表(4)
计量
- 文章访问数: 69
- HTML全文浏览量: 13
- PDF下载量: 16
- 被引次数: 0
