堆内构件正方形布置开圆孔平板结构辐照效应温升半解析解

林炳炽; 徐晓; 孔小飞; 刘攀; 金挺; 聂照宇; 鲁治诚; 姚博维

doi:10.13832/j.jnpe.2024.04.0096

堆内构件正方形布置开圆孔平板结构辐照效应温升半解析解

doi: 10.13832/j.jnpe.2024.04.0096

中广核工程有限公司核电安全技术与装备全国重点实验室，广东深圳，518172

详细信息

作者简介:
林炳炽（1992—），男，工程师，硕士研究生，现从事核岛设备力学分析研究，E-mail: 1498278415@qq.com

中图分类号: TL351⁺.1
计量
- 文章访问数: 55
- HTML全文浏览量: 19
- PDF下载量: 14
- 被引次数: 0
出版历程
- 收稿日期: 2023-08-15
- 修回日期: 2024-01-29
- 刊出日期: 2024-08-12

Semi-Analytical Solution of Temperature Rise Caused by Irradiation Effect for Perforated Plates with Square Penetration Patterns in Reactor Vessel Internals

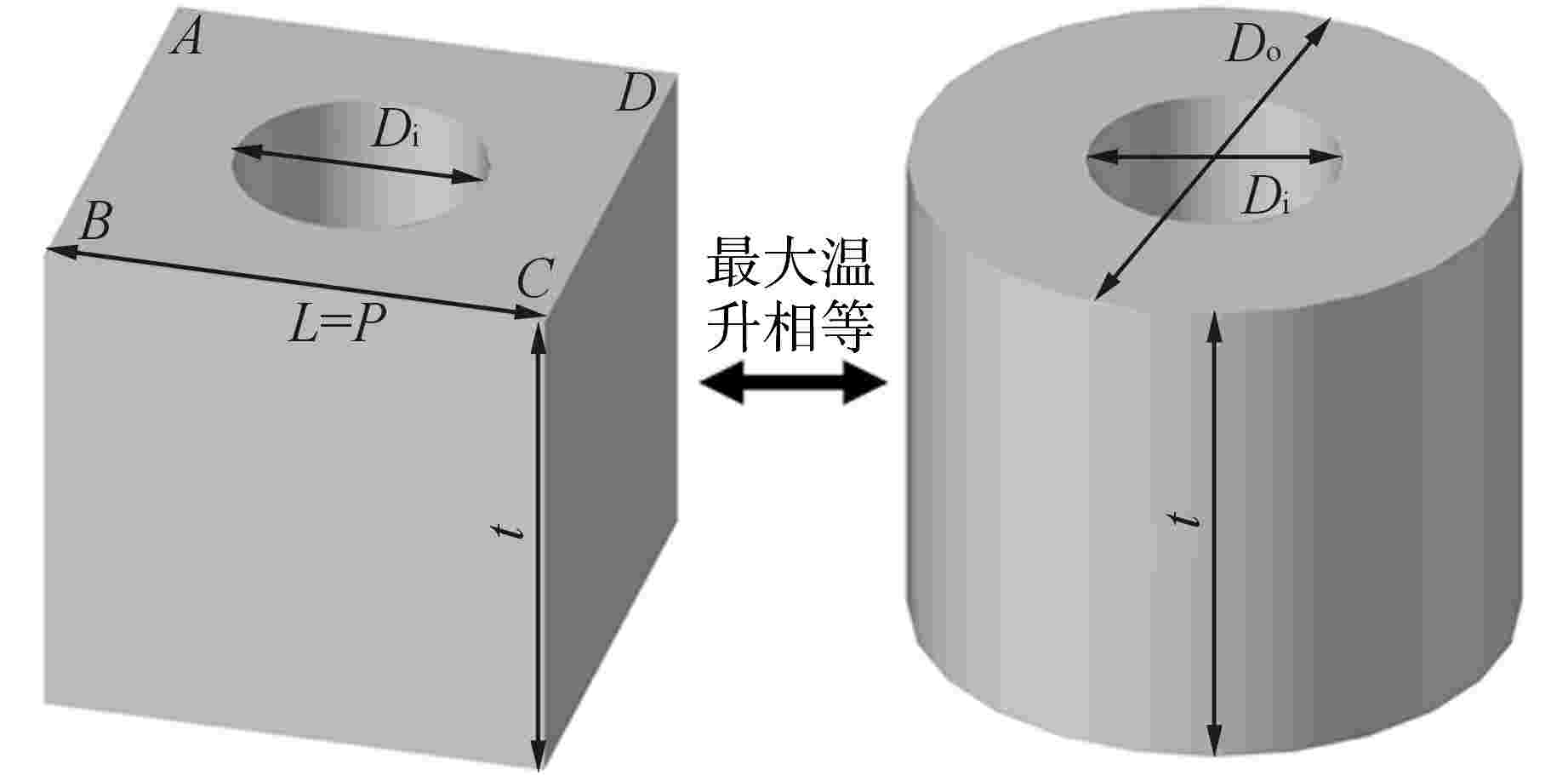
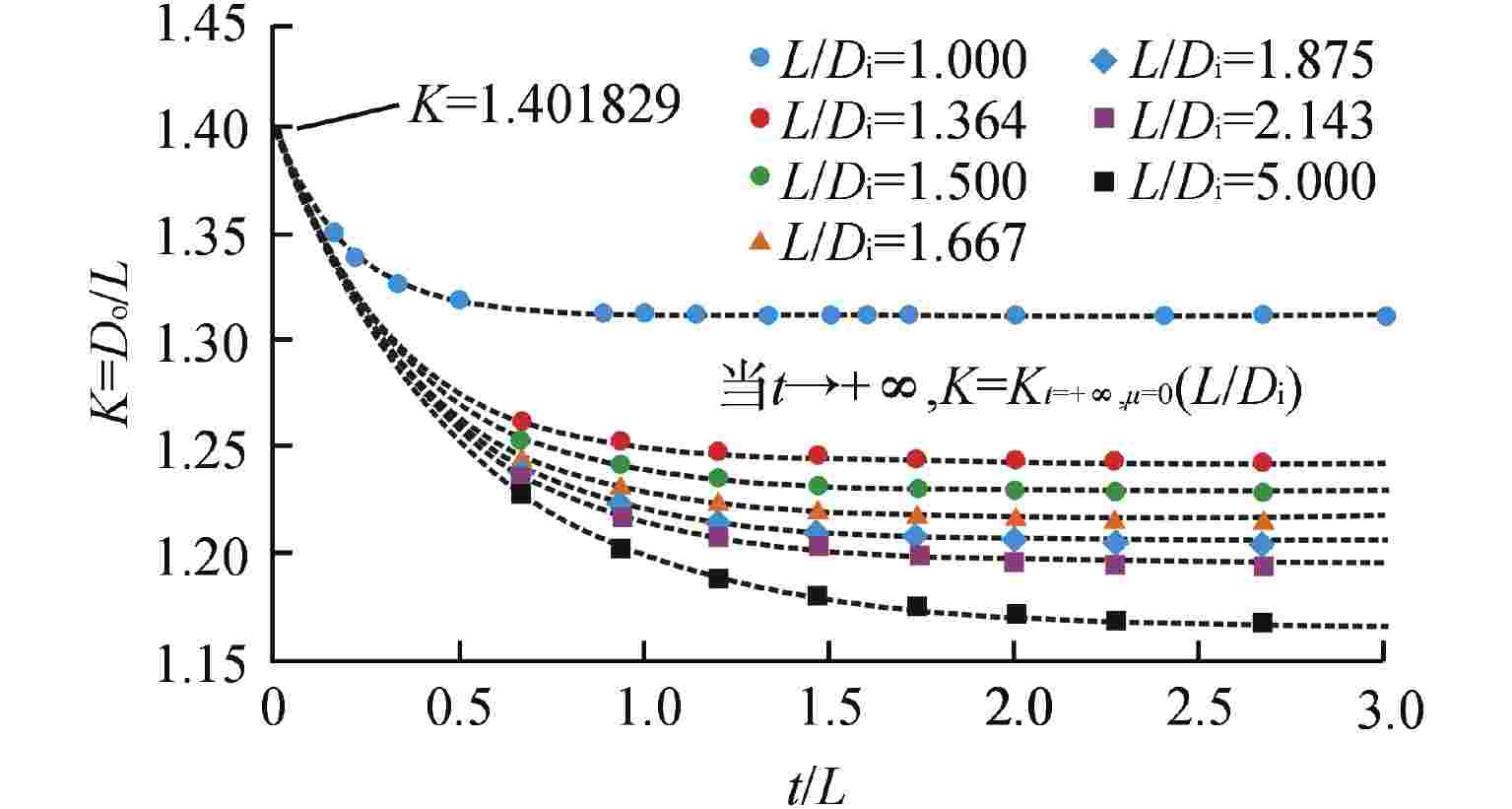
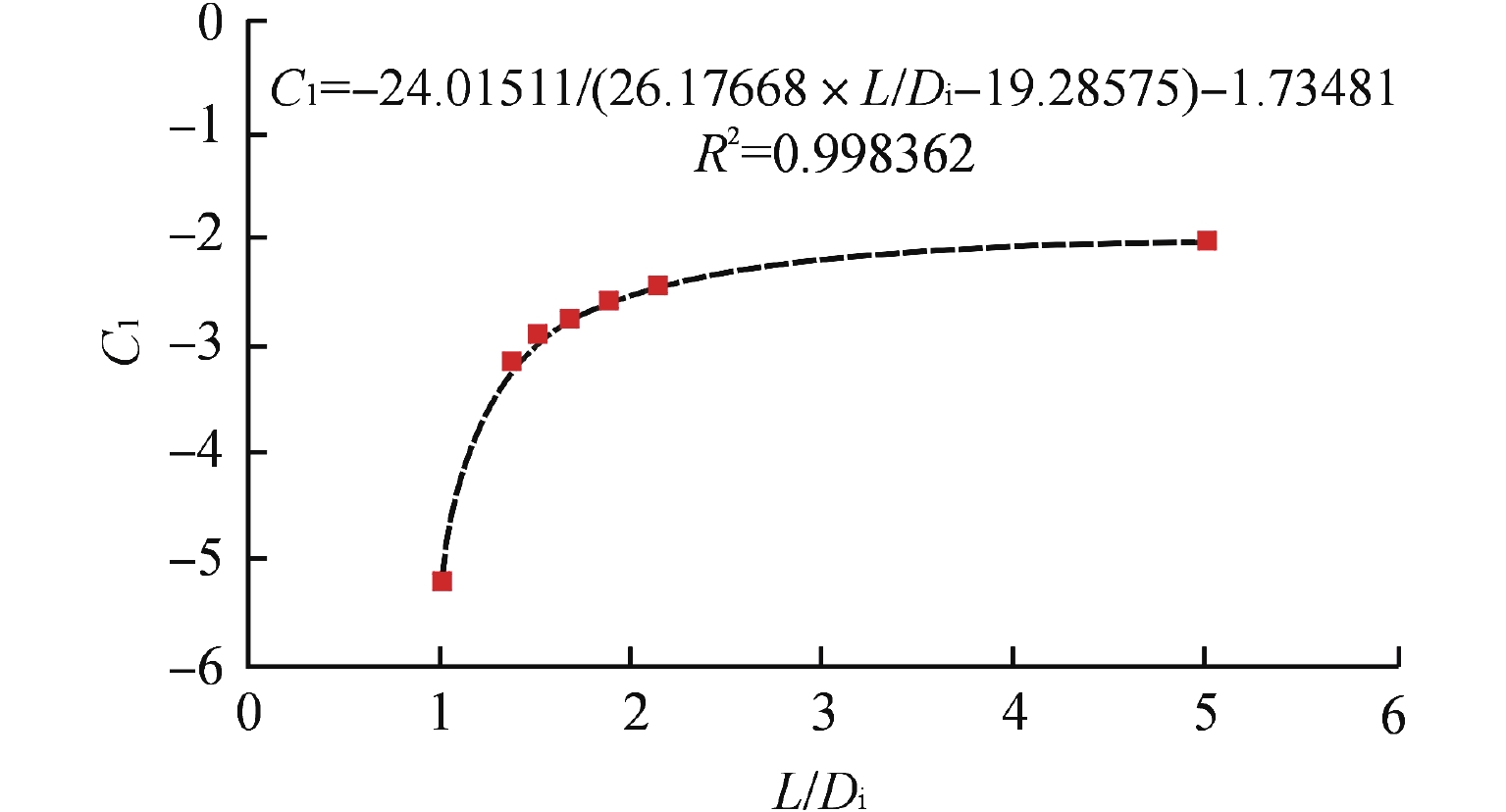
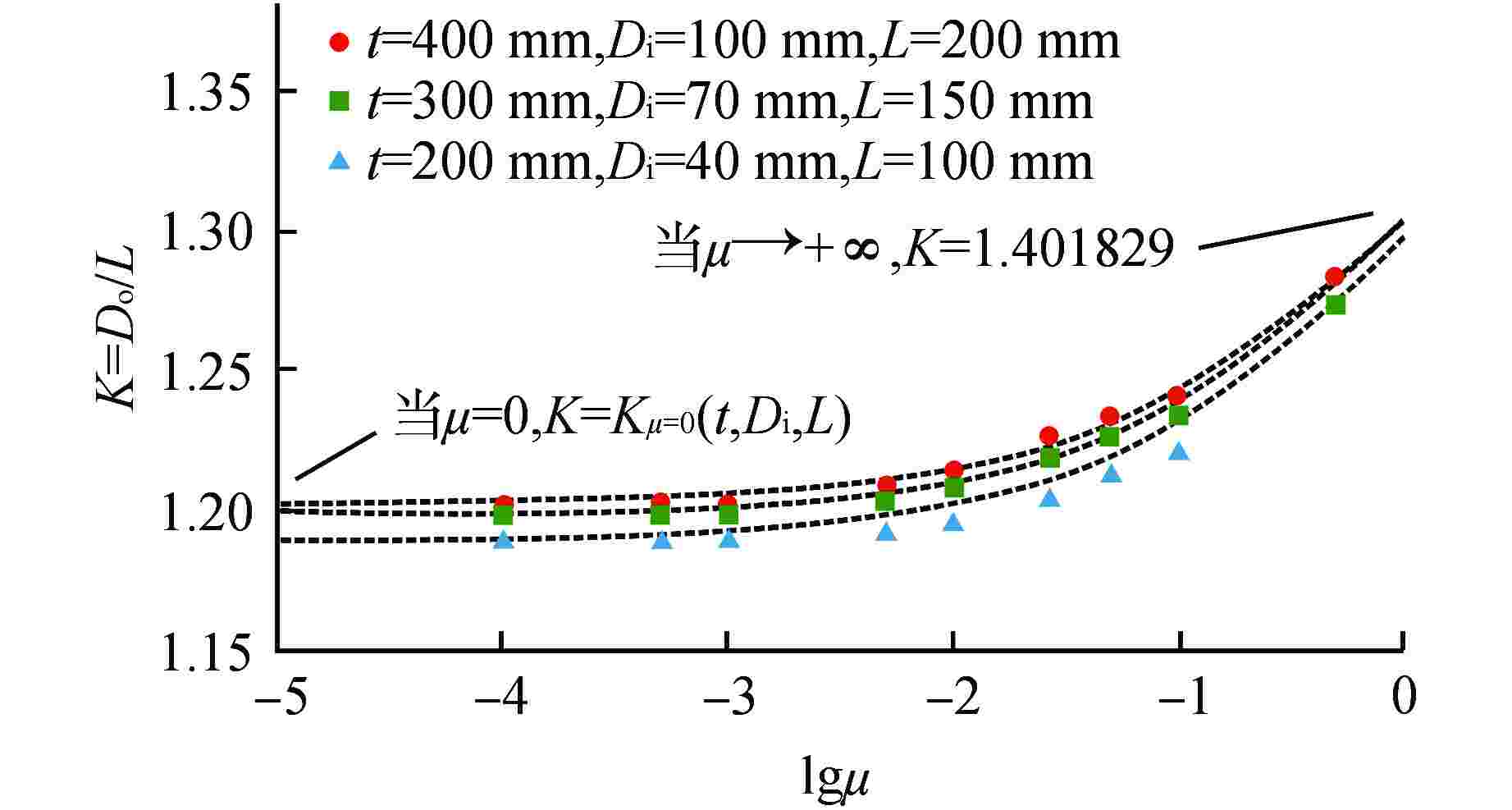
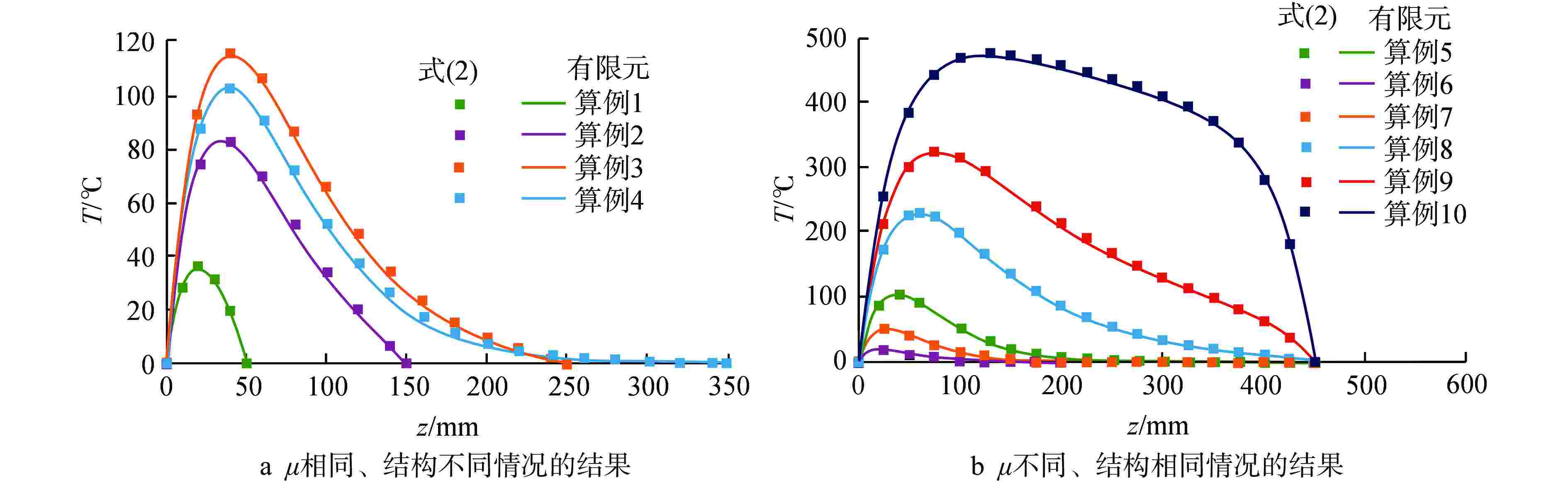
State Key Laboratory of Nuclear Power Safety Technology and Equipment, China Nuclear Power Engineering Co., Ltd., Shenzhen, Guangdong, 518172, China

摘要

摘要: 压水堆堆内构件中存在较厚的多孔板结构，其辐照效应带来的温升比较显著。由于结构的复杂性，其温升一般通过有限元方法计算得到。针对堆内构件正方形布置开圆孔平板结构，本文采用半解析方法计算其在辐照效应下的最大温升，得到了该结构的温升计算公式，并将其计算结果与有限元结果进行对比，结果表明：当γ释热率峰值的径向范围大于4倍孔心间距时，公式计算的最大温升与有限元结果偏差在2%以内，且公式计算的最大温升所在位置厚度方向的温度分布与有限元结果比较吻合。
- 辐照效应 /
- 堆内构件 /
- 多孔板 /
- 温升 /
- 半解析解
Abstract: In Reactor Vessel Internals (RVI), the temperature rise caused by the irradiation effect is significant for the thick perforated plates. Due to the complexity of the structure, its temperature rise is generally calculated by finite element method. In this paper, the semi-analytical method is used to calculate the maximum temperature rise of the perforated plate with square penetration patterns under irradiation effect. The calculation formula of the temperature rise of the structure is obtained, and the calculation results are compared with the finite element results. The results show that the deviation between the maximum temperature rise calculated by the formula and the finite element results is less than 2% when the radial range of the peak value of γ heat release rate is greater than 4 times the spacing between holes, and the temperature distribution in the thickness direction where the maximum temperature rise is calculated by the formula is in good agreement with the finite element results.
- Irradiation effect /
- Reactor vessel internals /
- Perforated plate /
- Temperature rise /
- Semi-analytical solution

HTML全文

图 1 正方形布置开圆孔平板结构示意

Figure 1. Perforated Plate with Square Penetration Patterns

下载: 全尺寸图片幻灯片

图 2 正方形圆孔结构和圆环结构示意图

D_o—圆环外直径

Figure 2. Square Structure of Circular Aperture and Ring Structure　　

下载: 全尺寸图片幻灯片

图 3 边长对外径的影响

Figure 3. Effect of Square Side Length on Outer Diameter

下载: 全尺寸图片幻灯片

图 4 厚度对外径的影响

Figure 4. Effect of Plate Thickness on Outer Diameter

下载: 全尺寸图片幻灯片

图 5 内径对外径的影响

Figure 5. Effect of Inner Diameter on Outer Diameter

下载: 全尺寸图片幻灯片

图 6 导热系数对外径的影响

Figure 6. Effect of Thermal Conductivity on Outer Diameter

下载: 全尺寸图片幻灯片

图 7 板表面的γ释热率对外径的影响

Figure 7. Effect of γ Generation Heat on Outer Diameter

下载: 全尺寸图片幻灯片

图 8 衰减系数对外径的影响

Figure 8. Effect of γ Attenuation Coefficient on Outer Diameter

下载: 全尺寸图片幻灯片

图 9 K与L/D_i的数据分布

Figure 9. Relation Curve of K and L/D_i

下载: 全尺寸图片幻灯片

图 10 不同的L/D_i下K与t/L的关系

Figure 10. Relation Curve of K and t/L with Different L/D_i

下载: 全尺寸图片幻灯片

图 11 C₁与L/D_i的关系

Figure 11. Relation Curve of C₁ and L/D_i

下载: 全尺寸图片幻灯片

图 12 K与lgμ的关系

Figure 12. Relation Curve of K and lgμ

下载: 全尺寸图片幻灯片

图 13 有限元模型示意图

Figure 13. Finite Element Models

下载: 全尺寸图片幻灯片

图 14 不同算例的厚度方向温度分布结果

Figure 14. Distribution of Temperature Rise Along Thickness for Different Cases

下载: 全尺寸图片幻灯片

表 1 算例列表

Table 1. List of Calculating Cases

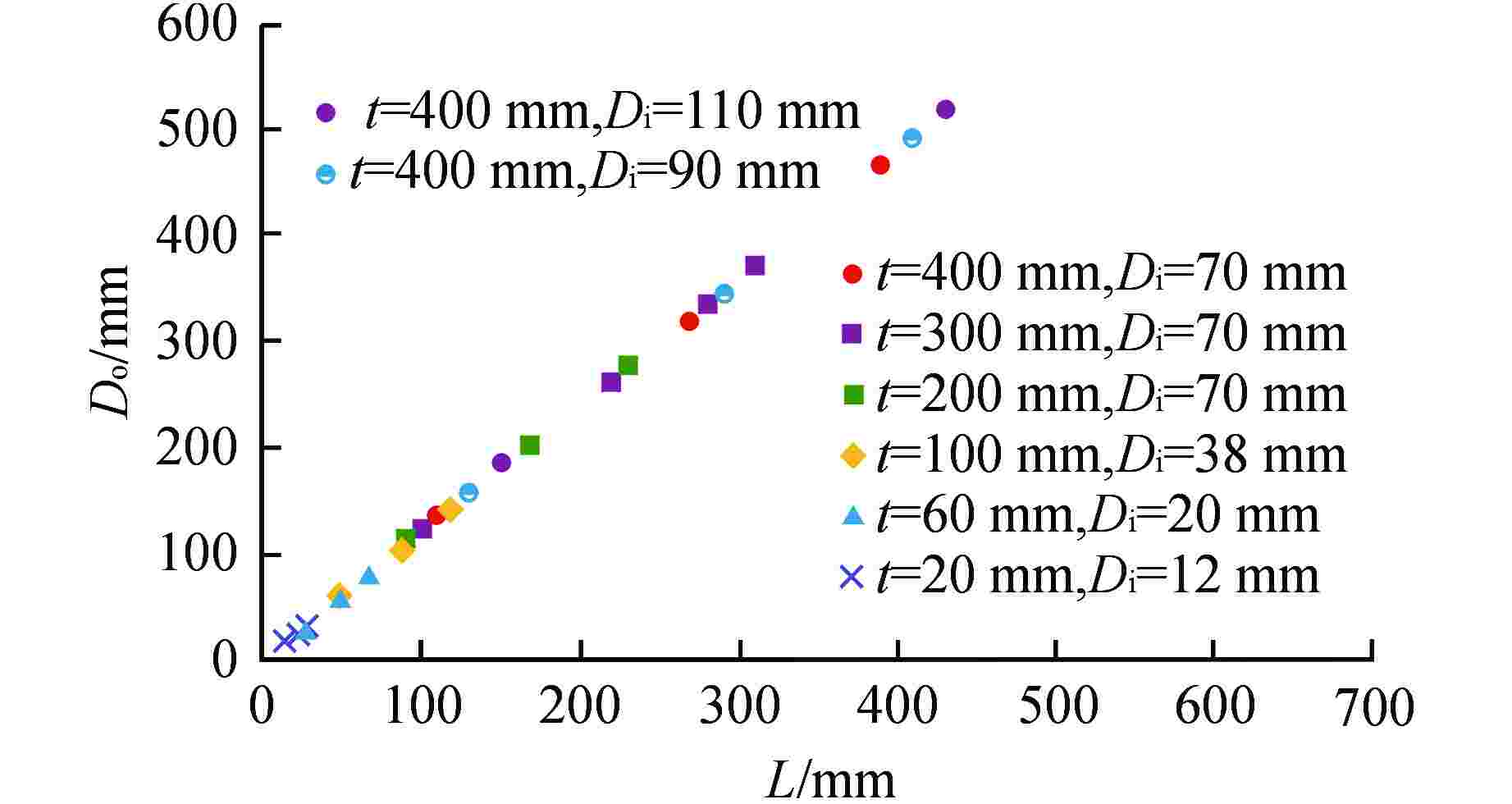
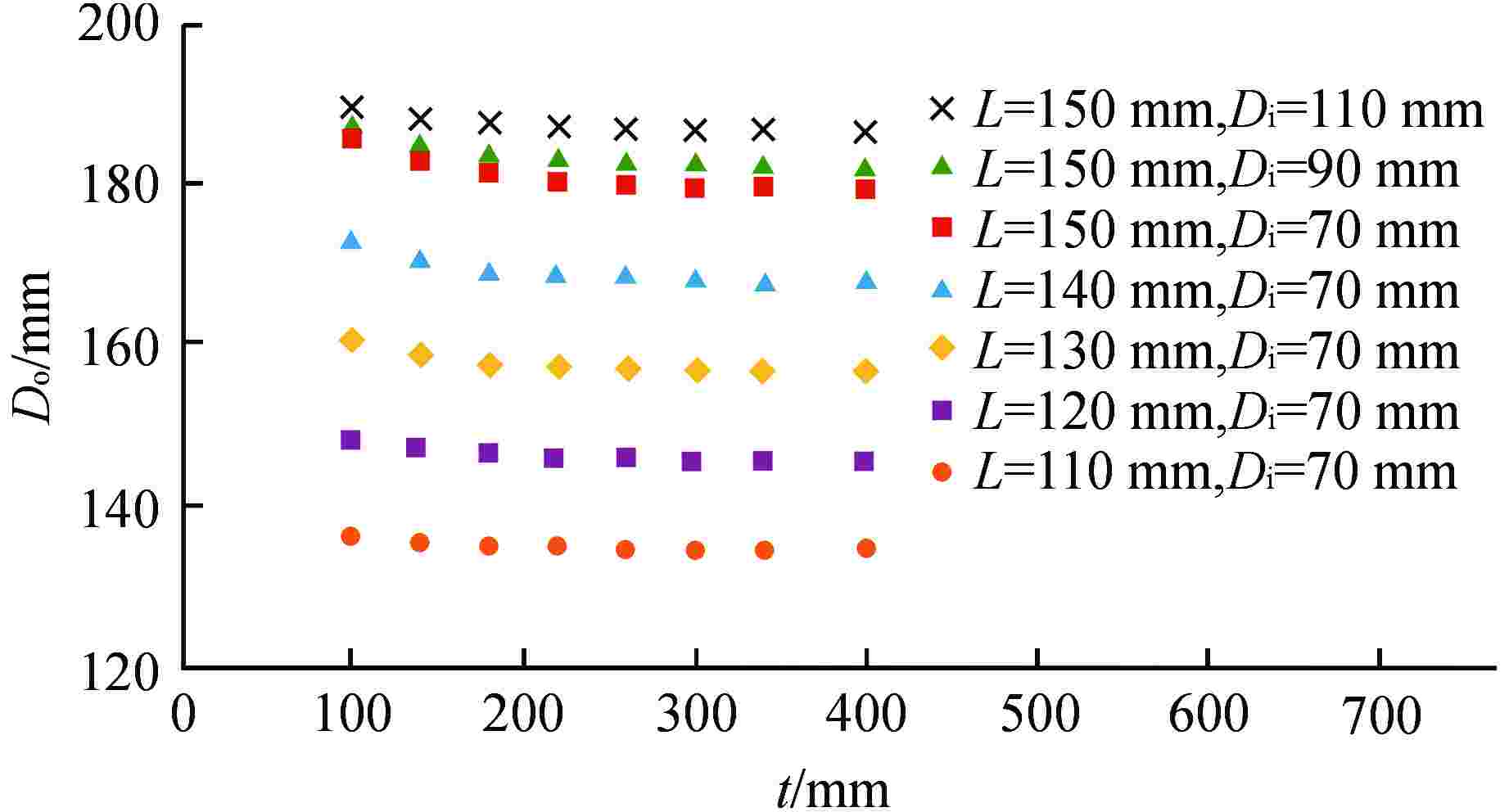
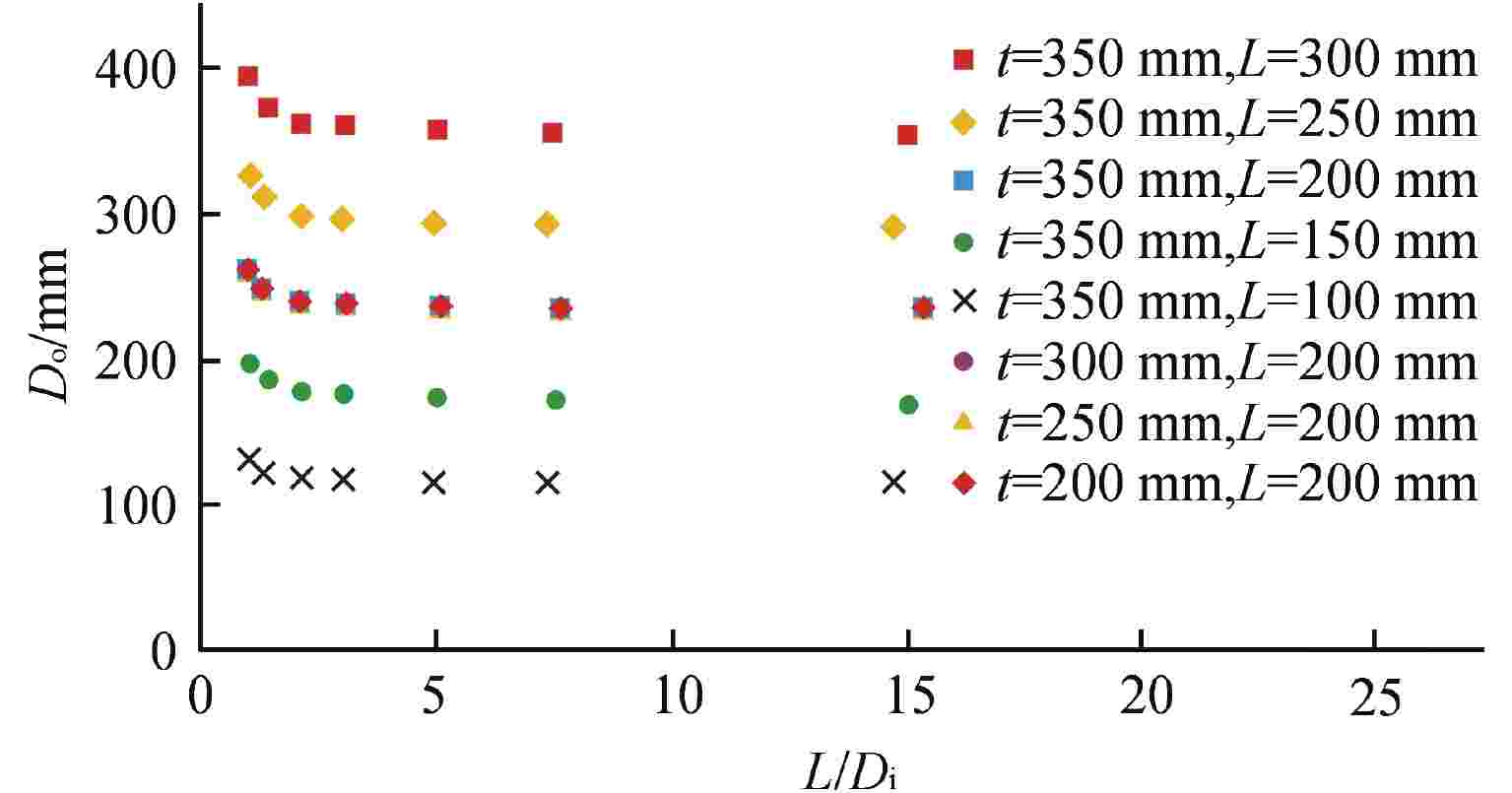
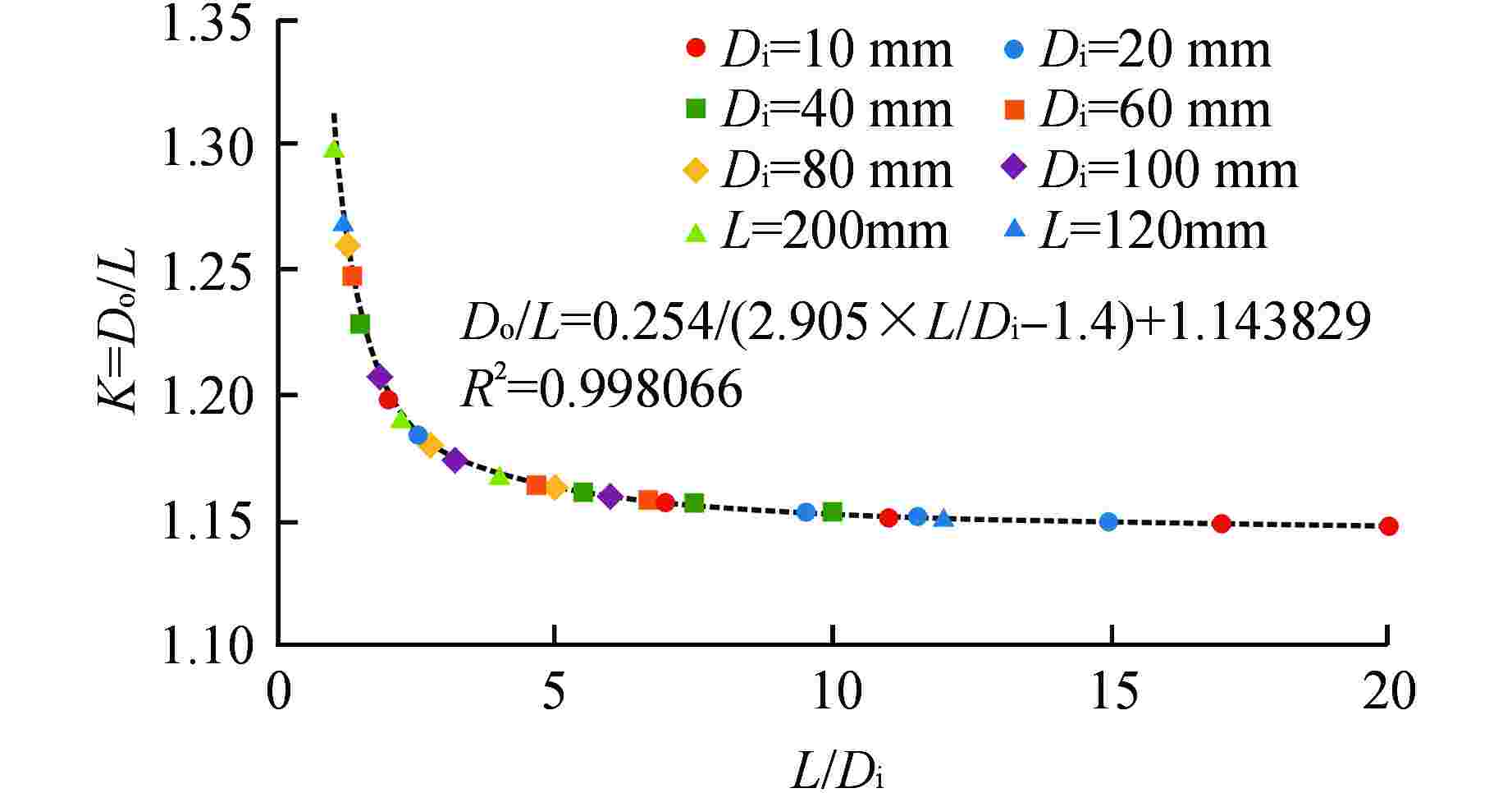
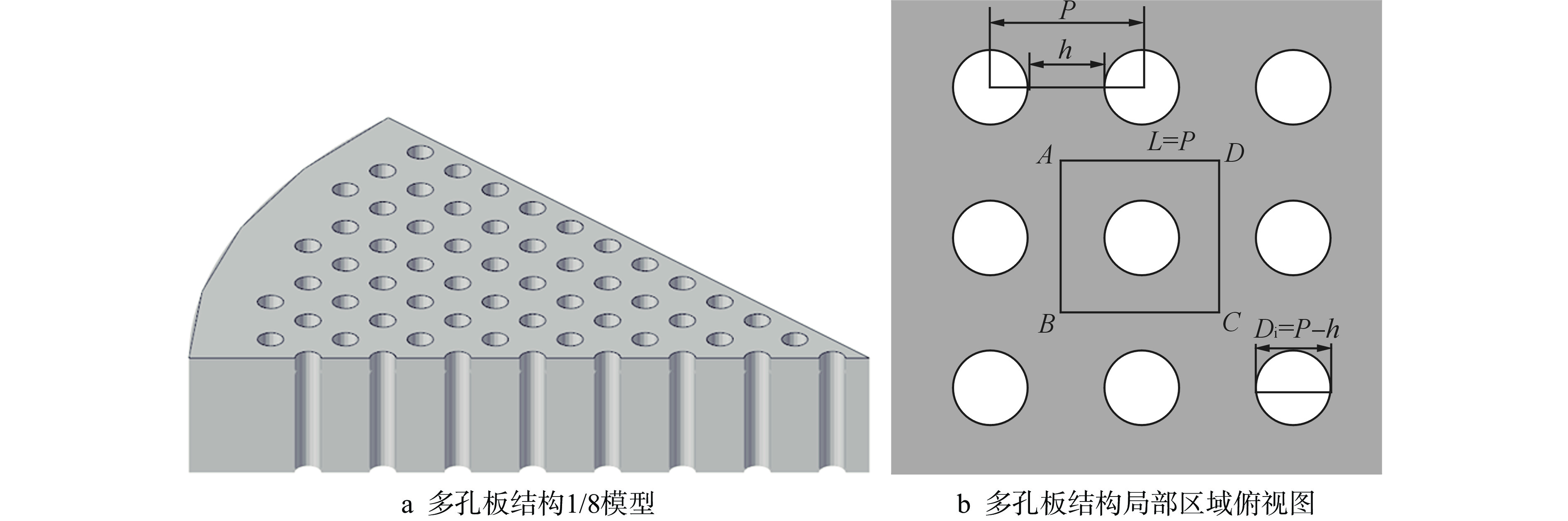
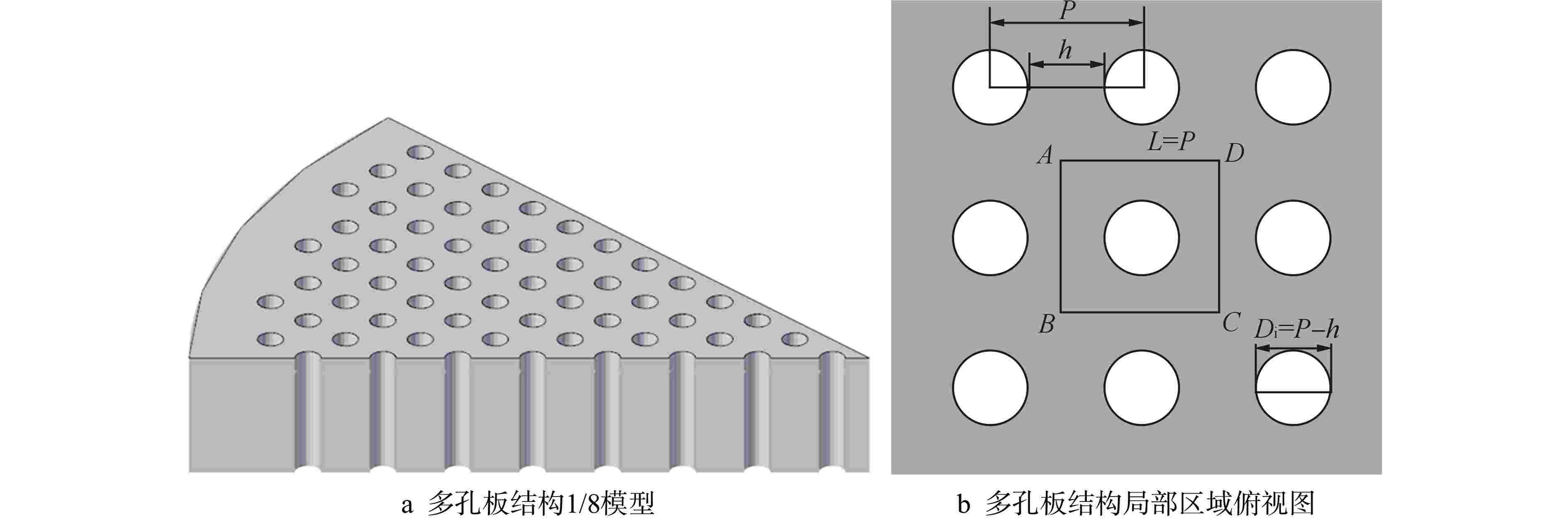
算例	P/mm	h/mm	t/mm	μ/mm⁻¹	D_o式(18)/mm
1	100	20	50	0.027	129.488
2	125	55	150	0.027	154.782
3	150	80	250	0.027	183.197
4	140	70	350	0.027	171.177
5	140	70	450	0.027	171.133
6	140	70	450	0.100	173.960
7	140	70	450	0.050	172.269
8	140	70	450	0.010	169.887
9	140	70	450	0.005	169.333
10	140	70	450	0.001	168.643

下载: 导出CSV

表 2 算例最大温升结果

Table 2. Maximum Temperature Rise for Each Calculating Case

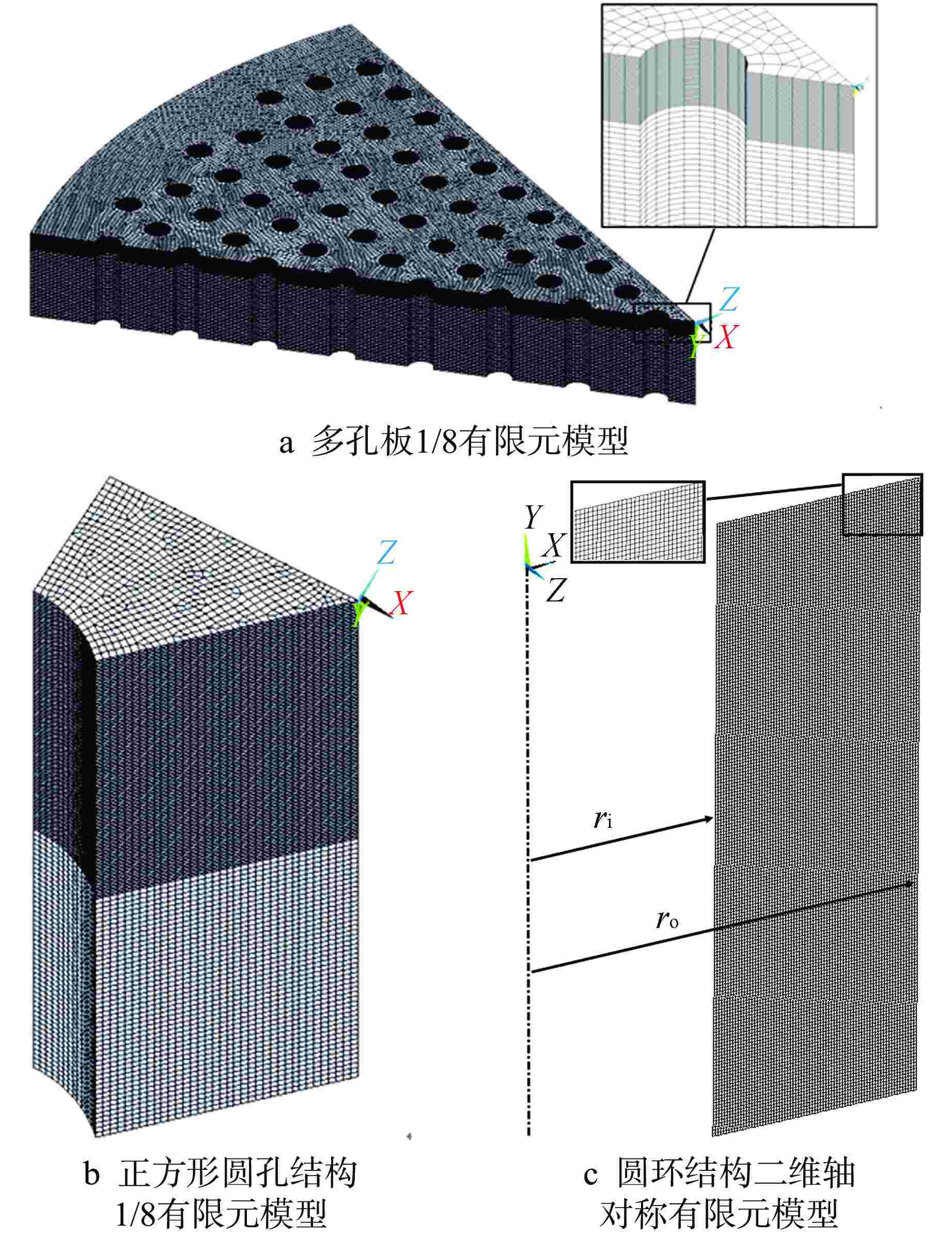
算例	最大温升/℃
	多孔板1/8 有限元模型		正方形圆孔结构 1/8有限元模型		圆环结构轴对称有限元模型		式（2）
	一阶单元	二阶单元	一阶单元	二阶单元	一阶单元	二阶单元	式（2）
1	36.32	35.55	35.50	35.40	36.08	36.44	36.08
2	83.63	83.70	83.30	83.27	84.34	84.34	84.33
3	115.14	115.46	115.06	115.04	115.42	115.41	115.41
4	103.05	103.22	102.82	102.79	102.84	102.84	102.83
5	103.09	103.22	102.82	102.79	102.80	102.79	102.78
6	18.97	18.94	18.93	18.91	18.98	18.97	18.97
7	50.73	50.71	50.58	50.55	50.58	50.57	50.57
8	228.97	230.02	228.71	228.65	229.47	229.48	229.48
9	322.37	324.54	322.31	322.30	324.39	324.41	324.41
10	471.56	476.01	472.07	472.02	476.62	476.66	476.66

下载: 导出CSV

表 3 算例结果相对偏差

Table 3. Relative Variation for Each Calculating Case

算例	相对偏差/%
	一阶单元相对二阶单元有限元结果			正方形圆孔结构相对多孔板有限元结果		圆环结构相对正方形圆孔结构有限元结果		式（2）相对圆环结构有限元结果		式（2）相对多孔板有限元结果
	多孔板	正方形圆孔结构	圆环结构	一阶单元	二阶单元	一阶单元	二阶单元	一阶单元	二阶单元	一阶单元	二阶单元
1	2.2	0.3	−1.0	−2.2	−0.4	1.6	2.9	0	−1.0	−0.6	1.5
2	−0.1	0	0	−0.4	−0.5	1.2	1.3	0	0	0.8	0.8
3	−0.3	0	0	−0.1	−0.4	0.3	0.3	0	0	0.2	0
4	−0.2	0	0	−0.2	−0.4	0	0	0	0	−0.2	−0.4
5	−0.1	0	0	−0.3	−0.4	0	0	0	0	−0.3	−0.4
6	0.1	0.1	0.1	−0.2	−0.2	0.3	0.3	0	0	0	0.1
7	0	0	0	−0.3	−0.3	0	0	0	0	−0.3	−0.3
8	−0.5	0	0	−0.1	−0.6	0.3	0.4	0	0	0.2	−0.2
9	−0.7	0	0	0	−0.7	0.6	0.7	0	0	0.6	0
10	−0.9	0	0	0.1	−0.8	1.0	1.0	0	0	1.1	0.1
注：A相对B的偏差=(A−B)/B×100%

下载: 导出CSV

参考文献(6)

[1]	李浩,李燕,何培峰,等. 华龙一号堆内构件设计方法研究[J]. 核动力工程,2022, 43(S2): 182-188.
[2]	束德林. 工程材料力学性能[M]. 第二版. 北京: 机械工业出版社,2007: 177.
[3]	梁昆淼. 数学物理方法[M]. 第四版. 北京: 高等教育出版社,2010: 143-178, 263-302.
[4]	凌备备,杨延洲. 核反应堆工程原理[M]. 北京: 原子能出版社,1982: 219.
[5]	刘玉坤,邢立国. 基于TensorFlow的线性回归模拟及Python实现[J]. 现代计算机,2018(29): 92-94. doi: 10.3969/j.issn.1007-1423.2018.29.020
[6]	陈豪,吴健. 基于神经网络的正弦波函数拟合实现研究[J]. 现代信息科技,2019, 3(21): 4-6. doi: 10.3969/j.issn.2096-4706.2019.21.003