A Reduced-Order Model of Mode Characteristics and Flow-Induced Vibration Response of Fuel Rod Based on POD Method
-
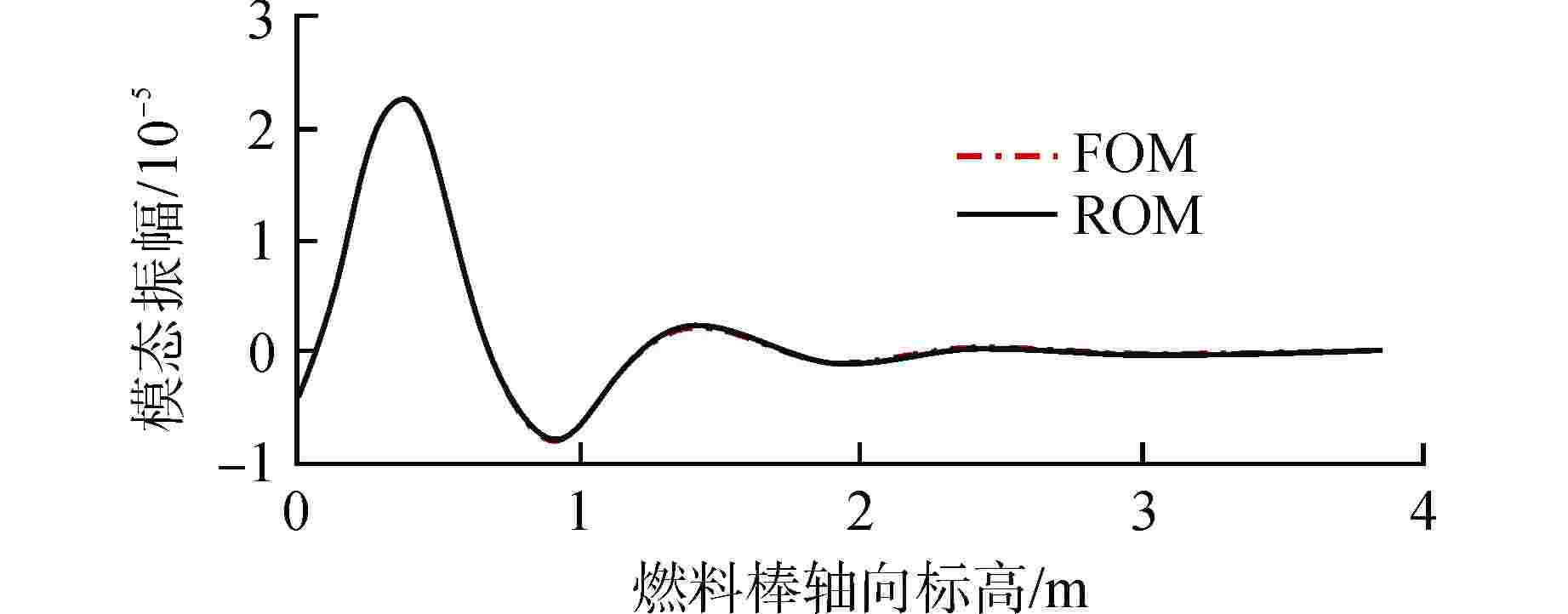
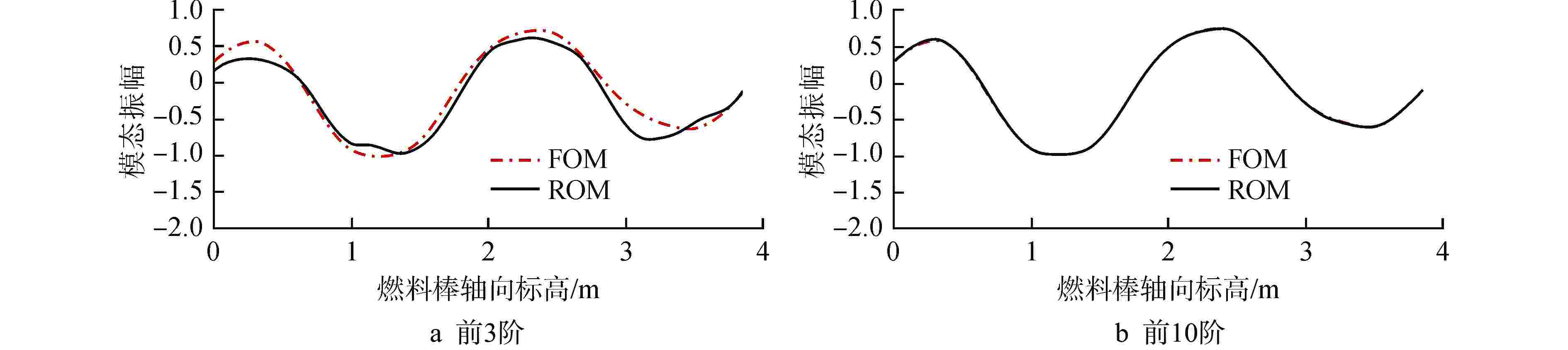
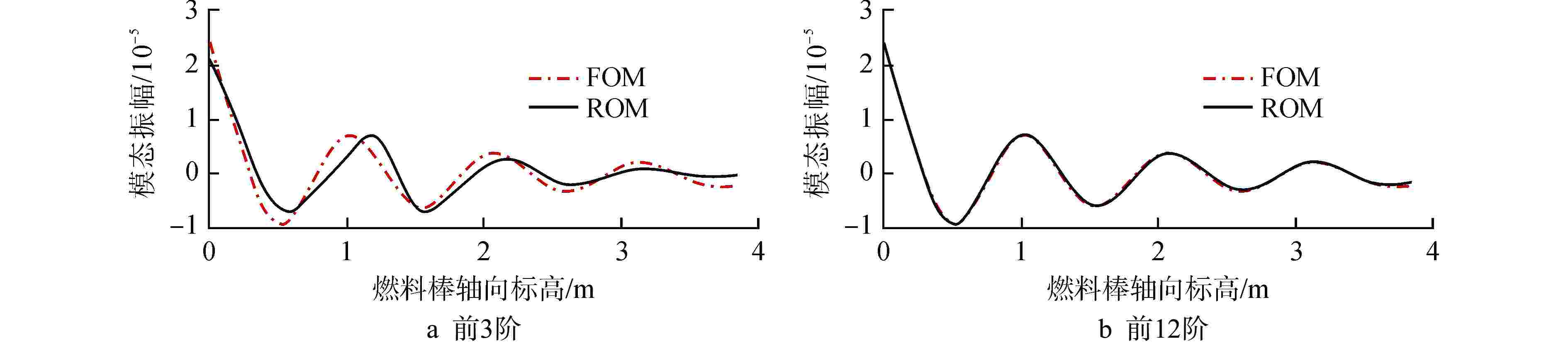
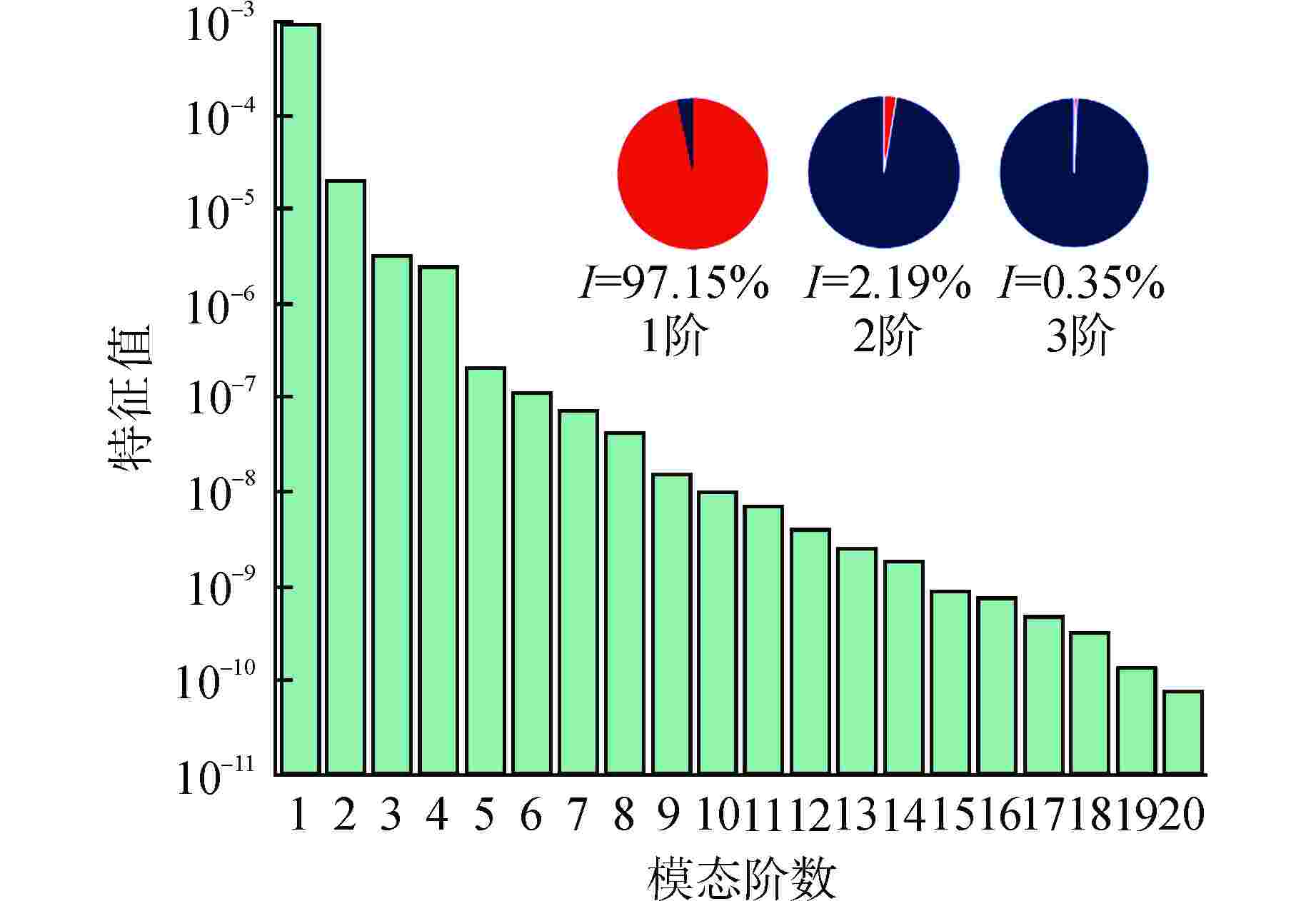
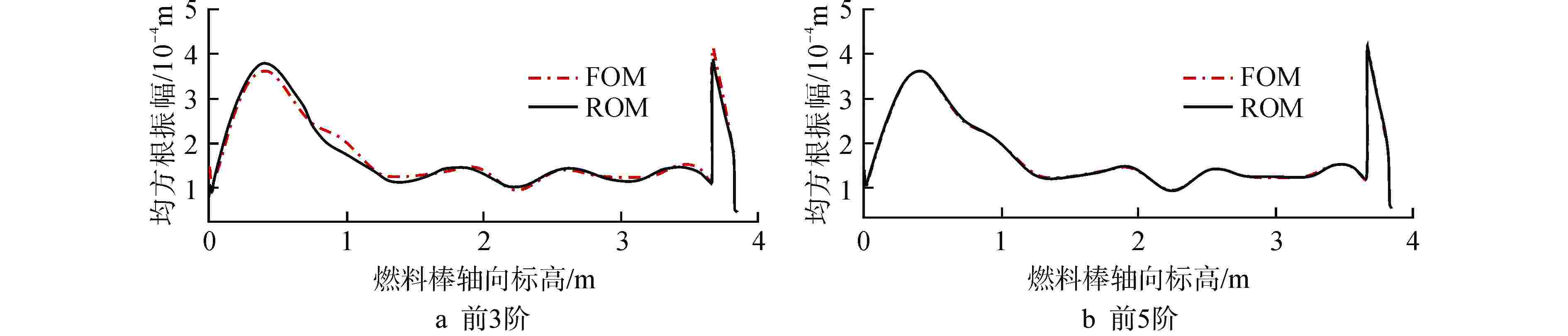
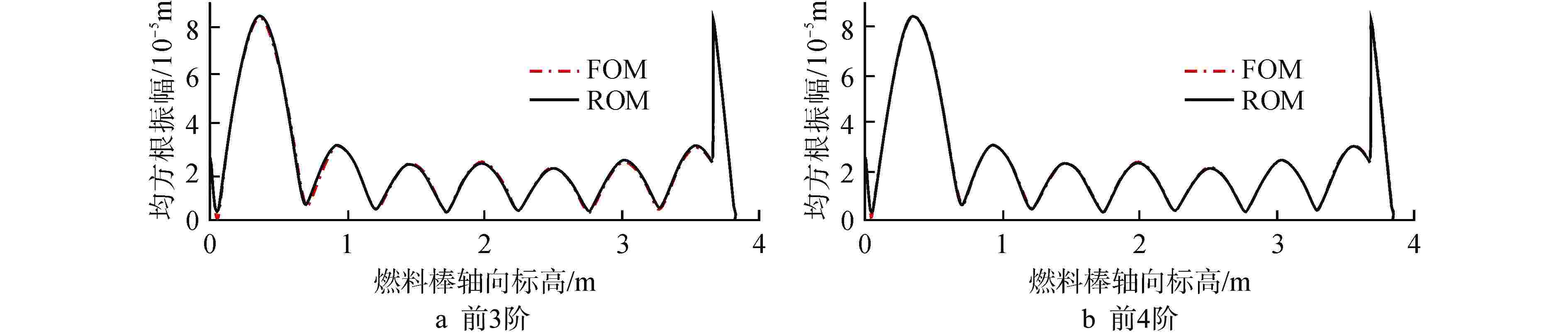
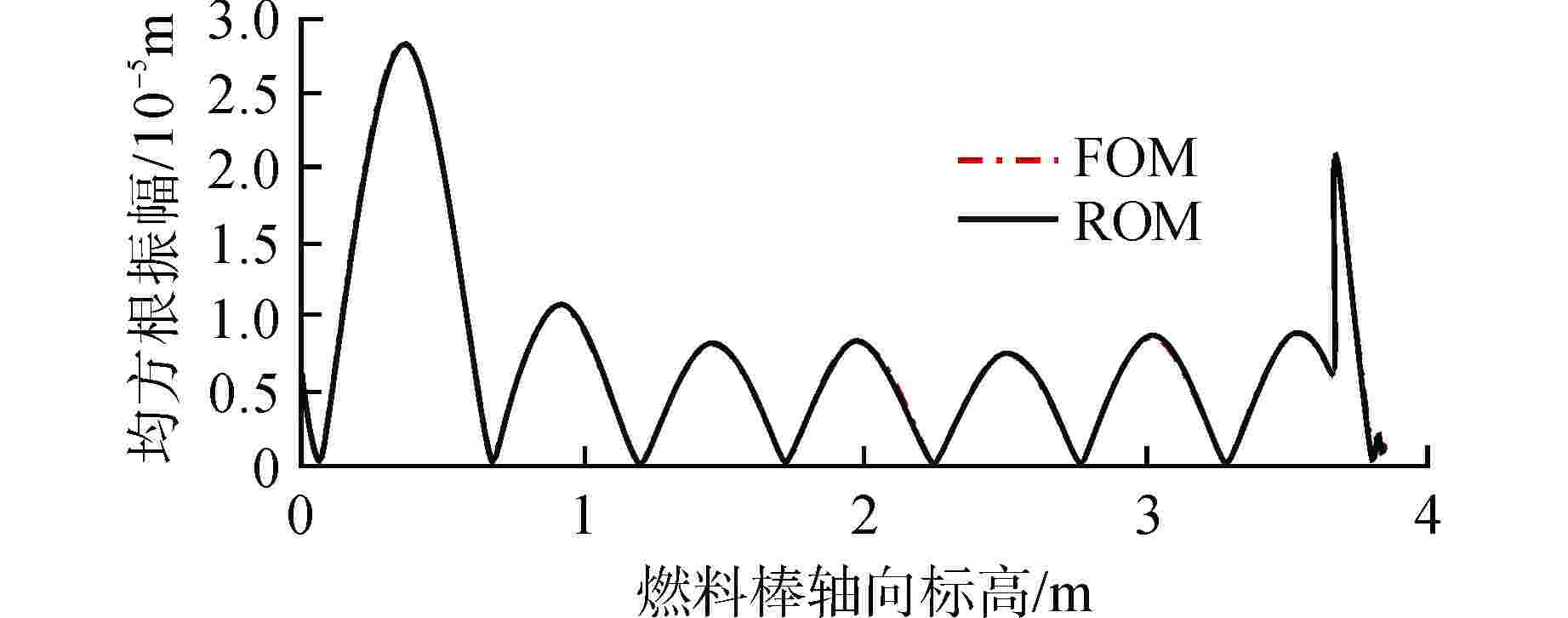
摘要: 本文搭建了一个快速预测燃料棒模态特征及流致振动响应的降阶模型（ROM）。首先，基于有限元分析软件ANSYS的批处理功能得到不同刚度下燃料棒的模态数据，将模态数据组装成快照矩阵。接着，基于商用数学软件MATLAB和半经验公式批量计算燃料棒的流致振动响应，将流致振动响应数据组装成快照矩阵。然后，采用本征正交分解（POD）方法将快照矩阵投影到低维空间，并根据特征值大小选出能量占比最高的POD模态。基于选出的POD模态将快照矩阵重构回物理空间，实现了模态和流致振动响应的快速计算。研究发现：对于1阶模态和流致振动响应的重构，刚度越小所需要的POD模态数量越多；对于相同刚度下不同阶模态的重构，模态阶次越高，所需要的POD模态数量越多。本文研究结果对于燃料棒模态特征和流致振动响应的快速计算具有一定的意义。
-
关键词:
- 本征正交分解(POD)方法 /
- 燃料棒 /
- 降阶模型(ROM) /
- 模态特征 /
- 流致振动响应
Abstract: A Reduced-Order Model (ROM) for swiftly predicting both the modes and flow-induced vibration response of fuel rods is introduced in this study. Firstly, modes for fuel rods with varying stiffness are obtained using ANSYS-Batch, and these modes are then compiled into a Snapshots matrix. Subsequently, leveraging MATLAB and semi-empirical formulas, the flow-induced vibration responses of fuel rods are batch-calculated, and the resulting data is assembled into another Snapshots matrix. The Proper Orthogonal Decomposition (POD) method is then applied to project the Snapshots matrix into a lower-dimensional space, with the POD modes having the highest energy contribution being selected based on the magnitude of eigenvalues. Finally, the Snapshots matrix is reconstructed back into physical space using the selected POD modes, enabling the rapid calculation of both mode and flow-induced vibration responses. Our study reveals that for reconstructing the first-order mode and flow-induced vibration responses, a smaller stiffness necessitates a greater number of POD modes. Furthermore, in the reconstruction of different-order modes with the same stiffness, higher-order modes require a greater number of POD modes. The findings of this study hold significance for the swift calculation of fuel rod mode characteristics and flow-induced vibration responses. -
图 3 模态特征ROM前 20 阶 POD 模态对应特征值
Figure 3. Eigenvalues of First 20 Order POD Modes of Mode Characteristics ROM
图 6 刚度977.24 N/mm下的1阶模态（前3阶）
Figure 6. 1st Order Mode with a Stiffness of 977.24 N/mm (First 3 Orders)
图 9 流致振动响应ROM前 20 阶 POD 模态对应特征值
Figure 9. Eigenvalues of First 20 Order POD Modes of Flow-induced Vibration Responses ROM
图 10 刚度1 N/mm下的流致振动响应
Figure 10. Flow-induced Vibration Response with a Stiffness of 1 N/mm
图 11 刚度9.77 N/mm下的流致振动响应
Figure 11. Flow-induced Vibration Response with a Stiffness of 9.77 N/mm
图 12 刚度977.24 N/mm下的流致振动响应（前3阶）
Figure 12. Flow-induced Vibration Response with a Stiffness of 977.24 N/mm (First 3 Orders)
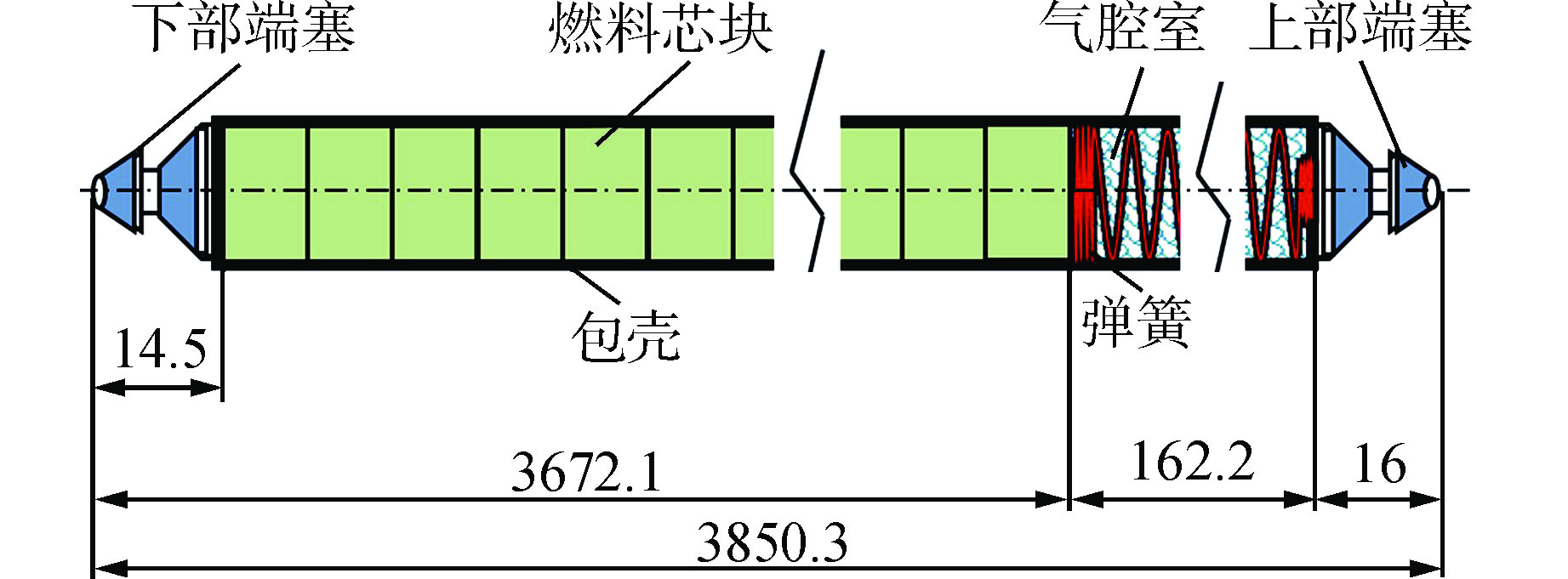
表 1 质量密度参数
Table 1. Mass Density Parameter
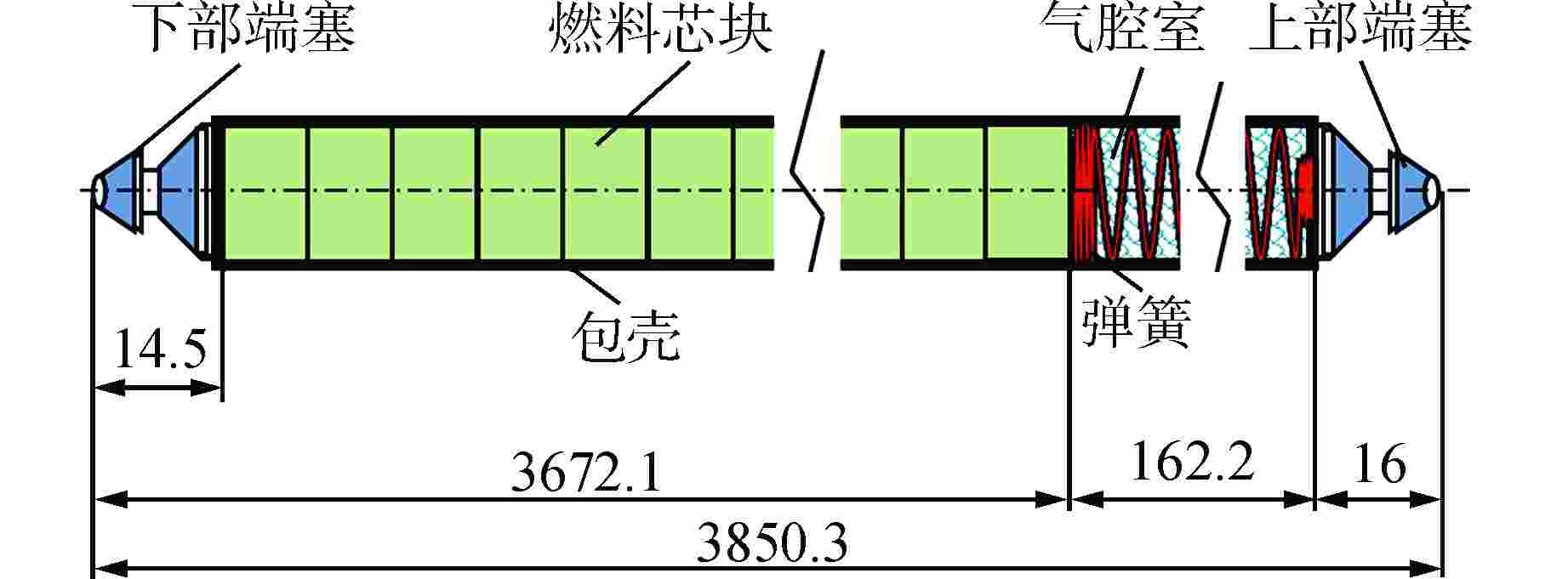
部位 质量密度/(kg·m−1) 端塞段 0.5792 芯块段 0.7936 气腔段 0.2224 
下载: 导出CSV
表 2 模态特征模型计算效率
Table 2. Computing Efficiency of Mode Characteristics Model
模型 时间/s FOM 60 ROM 1.2
下载: 导出CSV
表 3 流致振动响应模型计算效率
Table 3. Computing Efficiency of Flow-induced Vibration Response ROM
模型 时间/s FOM 560 ROM 60
下载: 导出CSV
-
[1] 赖姜,杨杰,席志德,等. 反应堆堆内构件流致振动特性研究[J]. 核动力工程,2016, 37(S2): 28-31. [2] KIM H K, LEE Y H, LEE K H. On the geometry of the fuel rod supports concerning a fretting wear failure[J]. Nuclear Engineering and Design, 2008, 238(12): 3321-3330. doi: 10.1016/j.nucengdes.2008.08.010 [3] KIM K T. The study on grid-to-rod fretting wear models for PWR fuel[J]. Nuclear Engineering and Design, 2009, 239(12): 2820-2824. doi: 10.1016/j.nucengdes.2009.08.018 [4] JIANG N B, MIN G Y, FANG Z Y, et al. Investigation on vibration response characteristics and influencing factors of the fuel rods of EPR[J]. Frontiers in Energy Research, 2022, 10: 990525. doi: 10.3389/fenrg.2022.990525 [5] 黄恒,刘彤,周跃民. 压水堆燃料棒在轴向流作用下的随机振动响应研究[J]. 原子能科学技术,2015, 49(3): 468-472. doi: 10.7538/yzk.2014.youxian.0006 [6] 黑宝平,高付海,李晓轩. 轴向流动液态钠中燃料元件的振动响应分析[J]. 地震工程与工程振动,2017, 37(4): 189-193. [7] 齐欢欢,冯志鹏,姜乃斌,等. 格架夹持失效对燃料棒流弹稳定性及漩涡脱落影响的数值研究[J]. 核动力工程,2018, 39(4): 182-186. [8] 齐欢欢,冯志鹏,姜乃斌,等. 格架松弛对燃料棒湍流激励及微振磨损的影响研究[J]. 原子能科学技术,2018, 52(10): 1810-1816. doi: 10.7538/yzk.2018.youxian.0066 [9] 齐欢欢,冯志鹏,吴万军,等. 压水堆燃料棒包壳微振磨损计算方法[J]. 核动力工程,2017, 38(5): 54-57. [10] 赵书峰,孙靖雅,徐时吟,等. 寿期末全尺寸燃料棒振动特性研究与验证[J]. 噪声与振动控制,2022, 42(3): 122-126. doi: 10.3969/j.issn.1006-1355.2022.03.021 [11] 朱勇,秦加明,任红兵,等. 基于ANSYS的蒸汽发生器传热管流致振动分析程序[J]. 核动力工程,2014, 35(4): 17-20. [12] SIROVICH L. Turbulence and the dynamics of coherent structures. III. Dynamics and scaling[J]. Quarterly of Applied Mathematics, 1987, 45(3): 583-590. doi: 10.1090/qam/910464 [13] 谢海润,吴亚东,欧阳华,等. 基于本征正交分解和动态模态分解的尾涡激振现象瞬态过程的模态分析[J]. 上海交通大学学报,2020, 54(2): 176-185. [14] 姜乃斌,冯志鹏,臧峰刚,等. 核工程中的流致振动理论与应用[M]. 上海: 上海交通大学出版社,2018: 183-229. -
计量
- 文章访问数: 32
- HTML全文浏览量: 9
- PDF下载量: 22
- 被引次数: 0
