Application of Green Function Method Considering Thermal Stratification Effect in Rapid Calculation of Fatigue Monitoring System
-
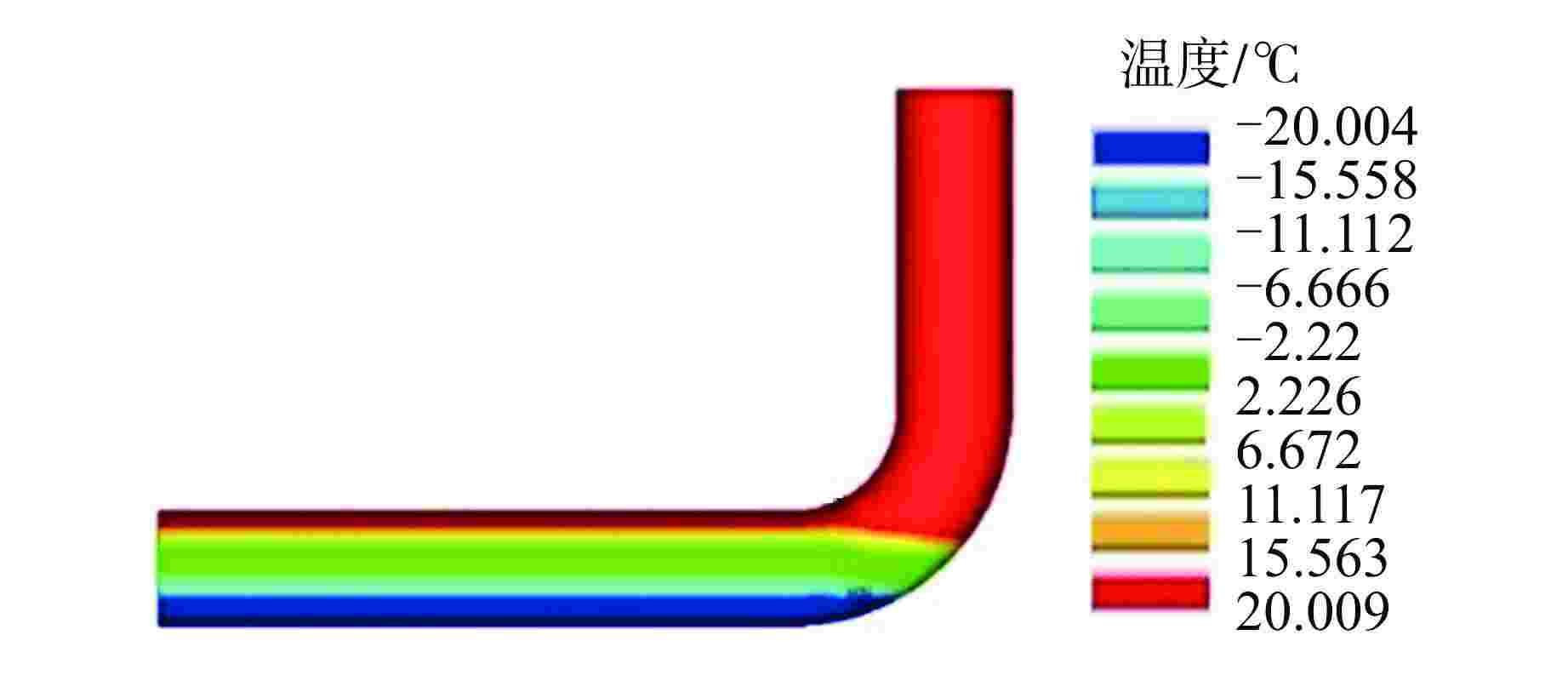
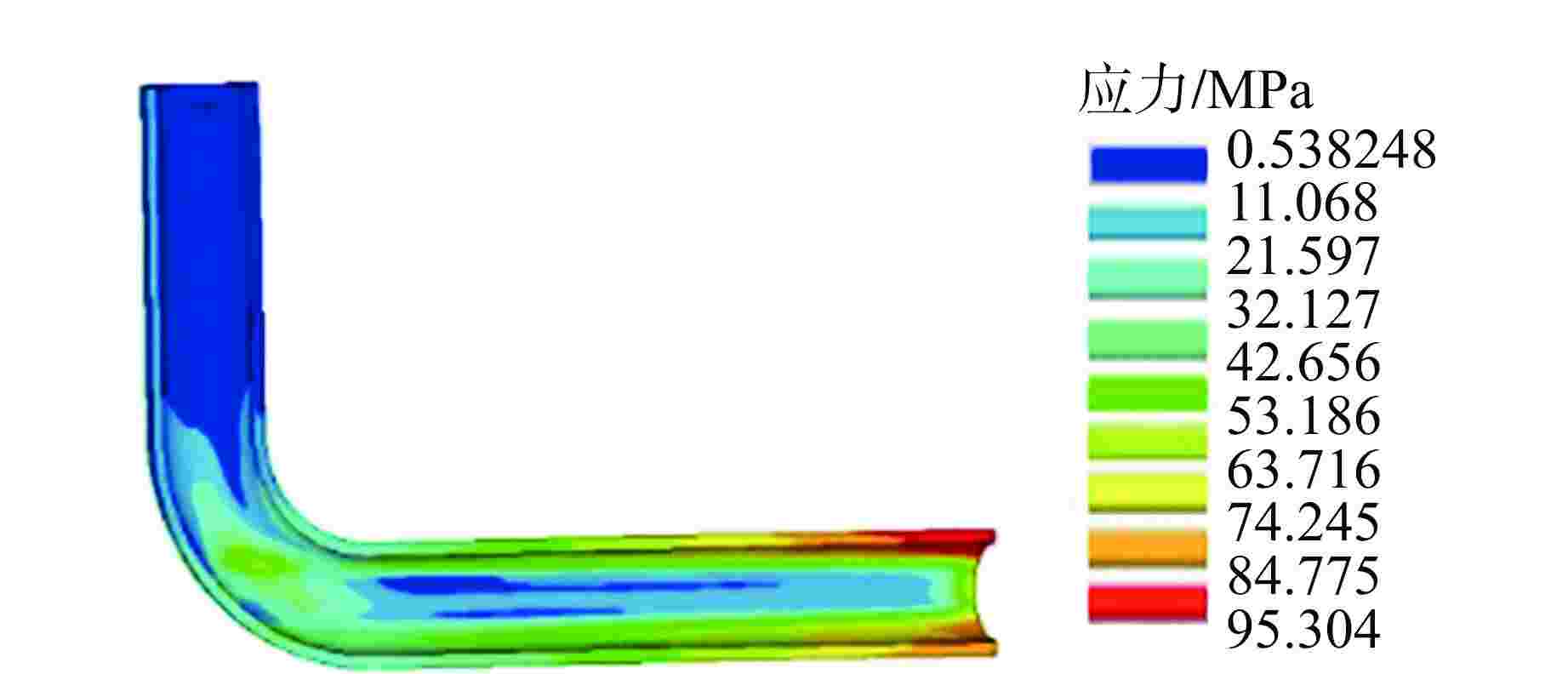
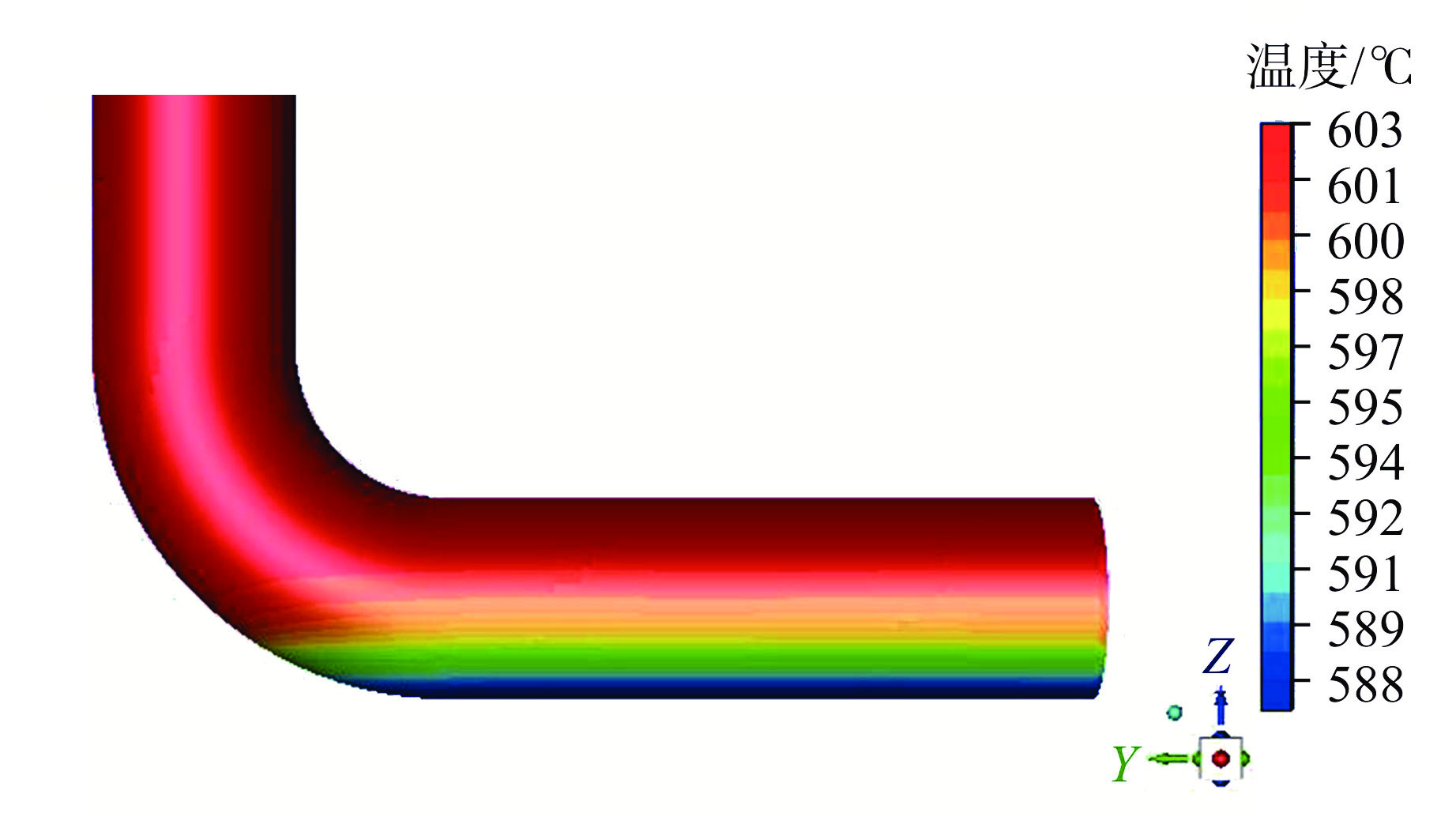
摘要: 针对在疲劳监测系统中考虑热分层效应的情况下如何实现快速计算展开了分析。提出了一种考虑热分层效应的格林函数计算方法，同时使用该方法针对波动管弯头模型在假定瞬态下的热分层应力进行了计算研究并与有限元方法进行了对比，验证本文方法的合理性和准确性。结果表明，本文提出的在格林函数基础上叠加考虑热分层效应的计算方法具有高效、快速、准确的特点，可应用于弯头拐角处的应力苛刻位置。目前该方法已应用于核电厂设备的疲劳监测系统。Abstract: This paper analyzes how to realize fast calculation when thermal stratification effect is considered in fatigue monitoring system. A new Green's function considering thermal stratification effect is proposed. At the same time, the thermal stratification stress of elbow model under assumed transient state is calculated by this method and compared with the finite element method, which shows that this method is reasonable and accurate. The results show that the calculation method based on Green's function and considering thermal stratification is efficient, fast and accurate, and can be applied to the stress servere position at the corner of elbow. At present, the method has been applied to the fatigue monitoring system of nuclear power plant equipment.
-
Key words:
- Thermal stratification /
- Green’s function /
- Fatigue monitoring system
-
图 1 波动管弯头热分层温度云图
Figure 1. Temperature Distribution of Thermal Stratification of Fluctuating Pipe Elbow
图 2 波动管热分层形式示意图
Figure 2. Schematic Diagram of Thermal Stratification of Fluctuating Pipe Elbow
图 4 热分层情形下的测点布置示意图
T1~T7—温度测点位置
Figure 4. Measuring Point Arrangement under Thermal Stratification
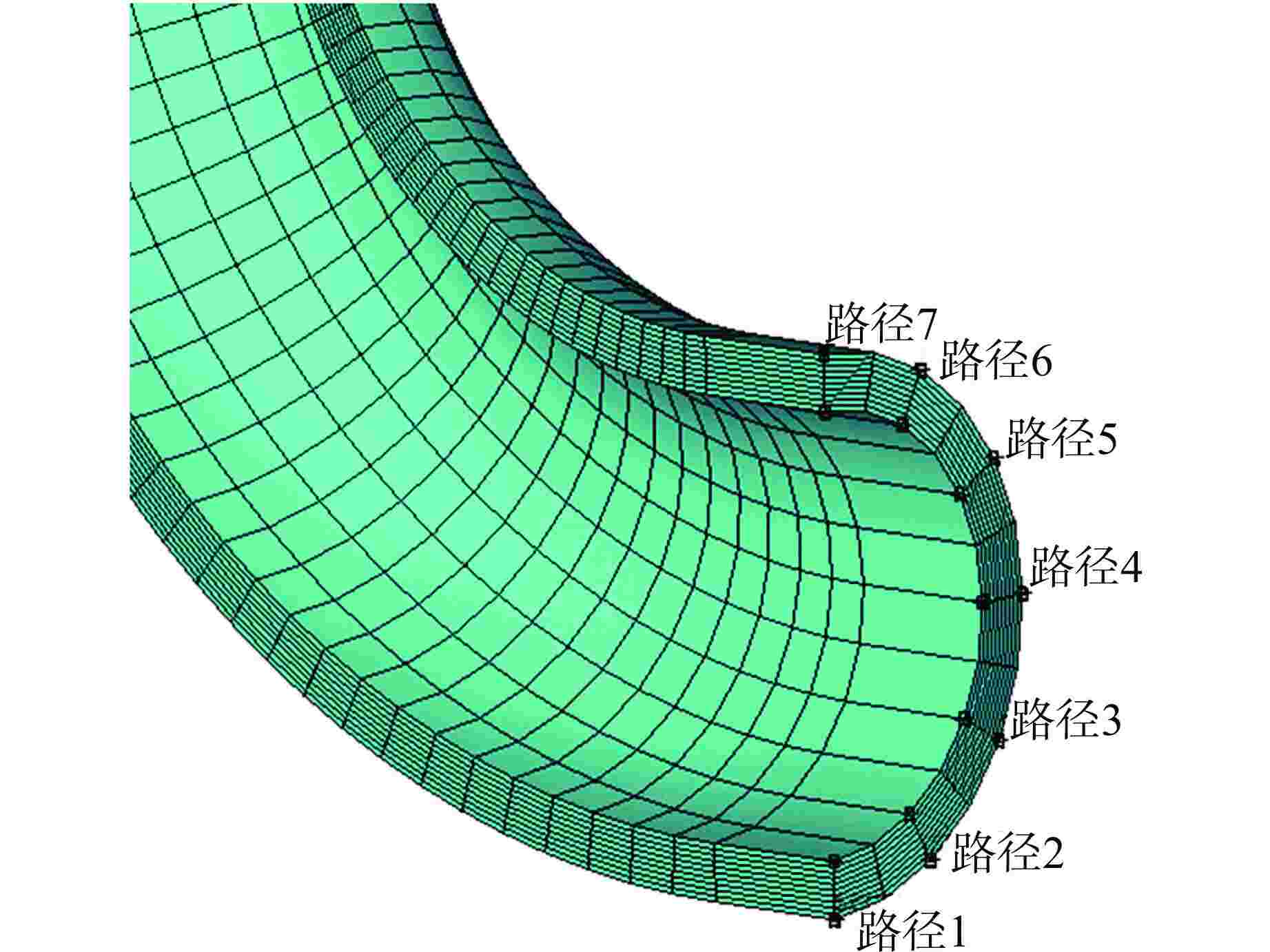
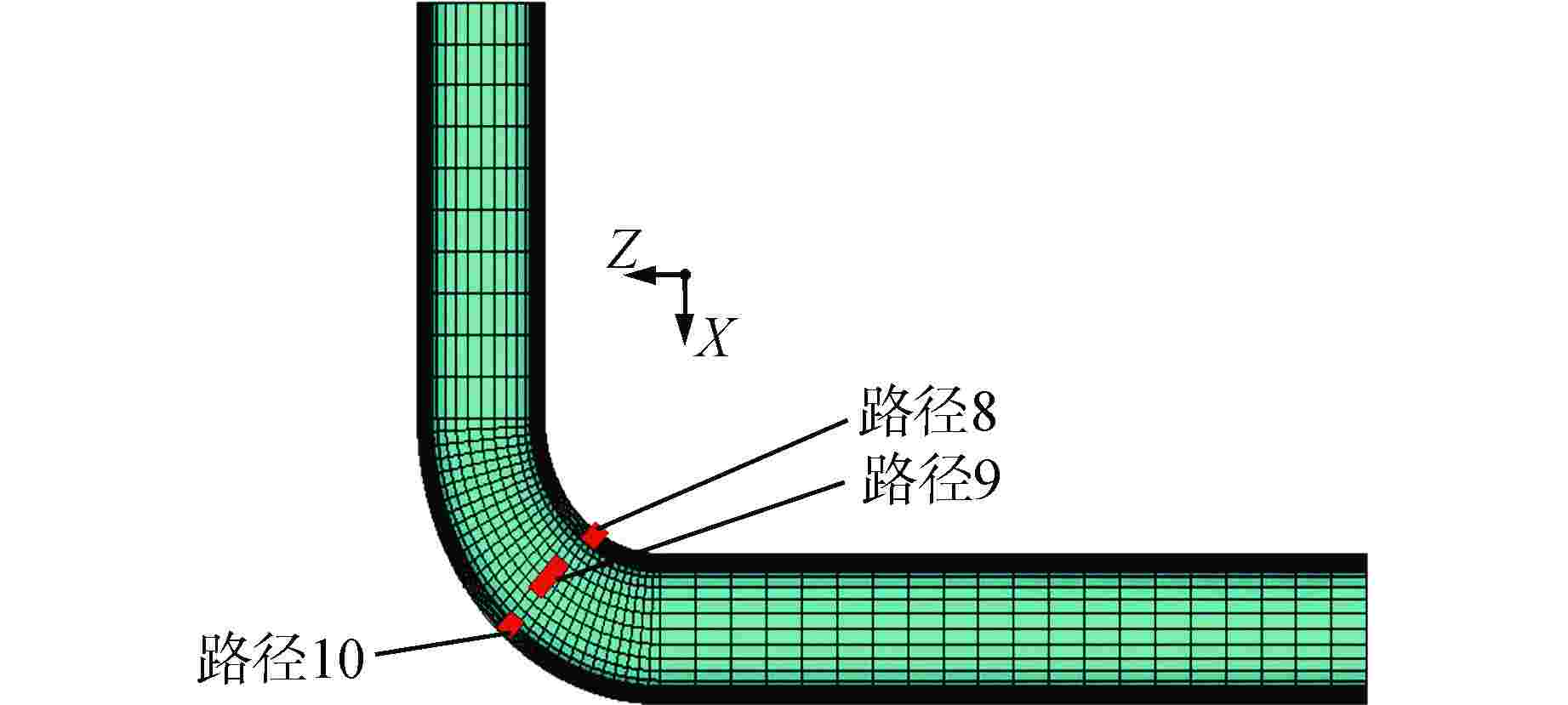
表 1 热应力幅值计算结果对比
Table 1. Comparison of Thermal Stress Amplitude
位置 应力分
量方向热应力幅值/MPa
（方法1：有限元方法）热应力幅值/MPa
（方法2：格林函数法）偏差①/% 路径1 X 59.151492 59.19166024 0.07 Y 220.148191 220.1738027 0.01 Z 220.213435 220.1644805 0.02 路径2 X 96.992859 99.47449043 2.56 Y 178.260045 180.1284378 1.05 Z 222.767364 220.2830805 1.12 路径3 X 179.091094 180.384704 0.72 Y 99.313388 99.49663339 0.18 Z 221.276937 220.3696414 0.41 路径4 X 221.378805 221.2208884 0.07 Y 58.984428 59.07562057 0.15 Z 221.203351 220.7701871 0.20 路径5 X 180.799335 180.3243118 0.26 Y 99.626172 99.46155576 0.17 Z 221.108225 220.8021094 0.14 路径6 X 99.483305 99.40346461 0.08 Y 180.265169 179.9402105 0.18 Z 220.883591 220.9359426 0.02 路径7 X 59.153544 59.17833812 0.04 Y 220.230311 219.8501928 0.17 Z 220.752571 220.8534525 0.05 路径8 X 154.869694 154.8035405 0.04 Y 216.225674 216.1278005 0.05 Z 121.436037 121.3968069 0.03 路径9 X 217.930556 217.9731243 0.02 Y 67.74353 67.74260812 0.00 Z 216.055493 216.1244956 0.03 路径10 X 157.411528 157.3650227 0.03 Y 220.783008 220.7122373 0.03 Z 123.904046 123.8428216 0.05 注：①偏差计算方法为：偏差=ǀ(方法2热应力幅值−方法1热应力幅值)/方法1热应力幅值ǀ。 
下载: 导出CSV
-
[1] 刘彤,王雪彩,衣书宾. 压水堆稳压器波动管热分层现象的流固耦合传热数值模拟[J]. 中国电机工程学报,2013, 33(2): 79-85. [2] 梁兵兵,李岗,王高阳. 稳压器波动管考虑热分层影响的疲劳分析[J]. 原子能科学技术,2008, 42(S2): 448-453. [3] 章贵和,段远刚,徐晓,等. 格林函数法在快速计算热应力中的应用研究[J]. 核动力工程,2013, 34(5): 45-47. doi: 10.3969/j.issn.0258-0926.2013.05.011 [4] 陈蓉,刘新,章贵和. 快速疲劳分析方法在核电厂疲劳监测系统中的应用[J]. 核动力工程,2018, 39(6): 59-63. [5] YU Y J, PARK S H, SOHN G H, et al. Structural evaluation of thermal stratification for PWR surge line[J]. Nuclear Engineering and Design, 1997, 178(2): 211-220. doi: 10.1016/S0029-5493(97)00224-0 [6] XU X, LIU P, ZHANG G H, et al. Thermal stratification analysis and fatigue evaluation for pressurizer surge line in nuclear power plant[C]//Proceedings of the 2017 25th International Conference on Nuclear Engineering. Shanghai: ASME, 2017. [7] AFCEN. Design and construction rules for mechanical components of PWR nuclear islands[S]. France: AFCEN. 2004: 37-40. [8] 刘浪,凌君,曹雷生,等. 单位瞬态法在核电厂疲劳监测系统中的应用[J]. 原子能科学技术,2017, 51(6): 1051-1058. -
计量
- 文章访问数: 41
- HTML全文浏览量: 15
- PDF下载量: 14
- 被引次数: 0
