Study on Orthogonal Experiments of Jet Breakup and its Modeling Based on MPS Method
-
摘要: 为了研究堆芯熔融物射流破裂过程中射流破裂长度的主要影响因素及其作用程度评级，基于正交实验法设计了3因素5水平的25组实验，采用移动粒子半隐式仿真（MPS）得到各工况下的射流破裂长度，并对模拟结果进行极差与方差分析，结果表明，影响射流破裂长度的主要因素为射流与冷却剂密度比、射流速度和射流直径，三者的显著性均为二级（**），在同级别中的作用程度大小依次为：射流速度>射流与冷却剂密度比>射流直径。在此基础上使用模拟数据拟合出了新的预测射流破裂长度经验关系式，当射流与冷却剂密度比为1.1~13.6时，该关系式的预测误差控制在±30%范围内。Abstract: In order to study the primary influencing factors of jet breakup length during the core melt jet breakup process and their ranking, 25 sets of experiments with 3 factors and 5 levels were designed based on the orthogonal experimental method, and the jet breakup lengths were obtained for each condition by using the Moving Particle Semi-implicit method (MPS). The simulation results were analyzed by polarity and variance analysis, and it was concluded that the primary influencing factors of jet breakup length were jet to coolant density ratio, jet velocity and jet diameter, and all of them have a second level of significance (**). Their ranking in the same level was in the following order: jet velocity > jet to coolant density ratio > jet diameter. Moreover, a new empirical relationship for predicting jet breakup length was fitted using simulated data, and the error margin of the model was kept within ±30% when the ratio of jet to coolant density was 1.1~13.6.
-
Key words:
- Jet breakup length /
- Influencing factors /
- Orthogonal experiments /
- Empirical correlation
-
图 2 不同粒子直径和参考实验的射流穿透深度
Figure 2. Jet Penetration Depth for Different Particle Diameter Sizes and Reference Experiments
图 3 数值模拟和参考实验的伍德合金射流形态
红色区域—数值模拟结果，灰色区域—参考实验结果
Figure 3. Morphology of Wood’s Alloy Jet for Value Simulation and Reference Experiments
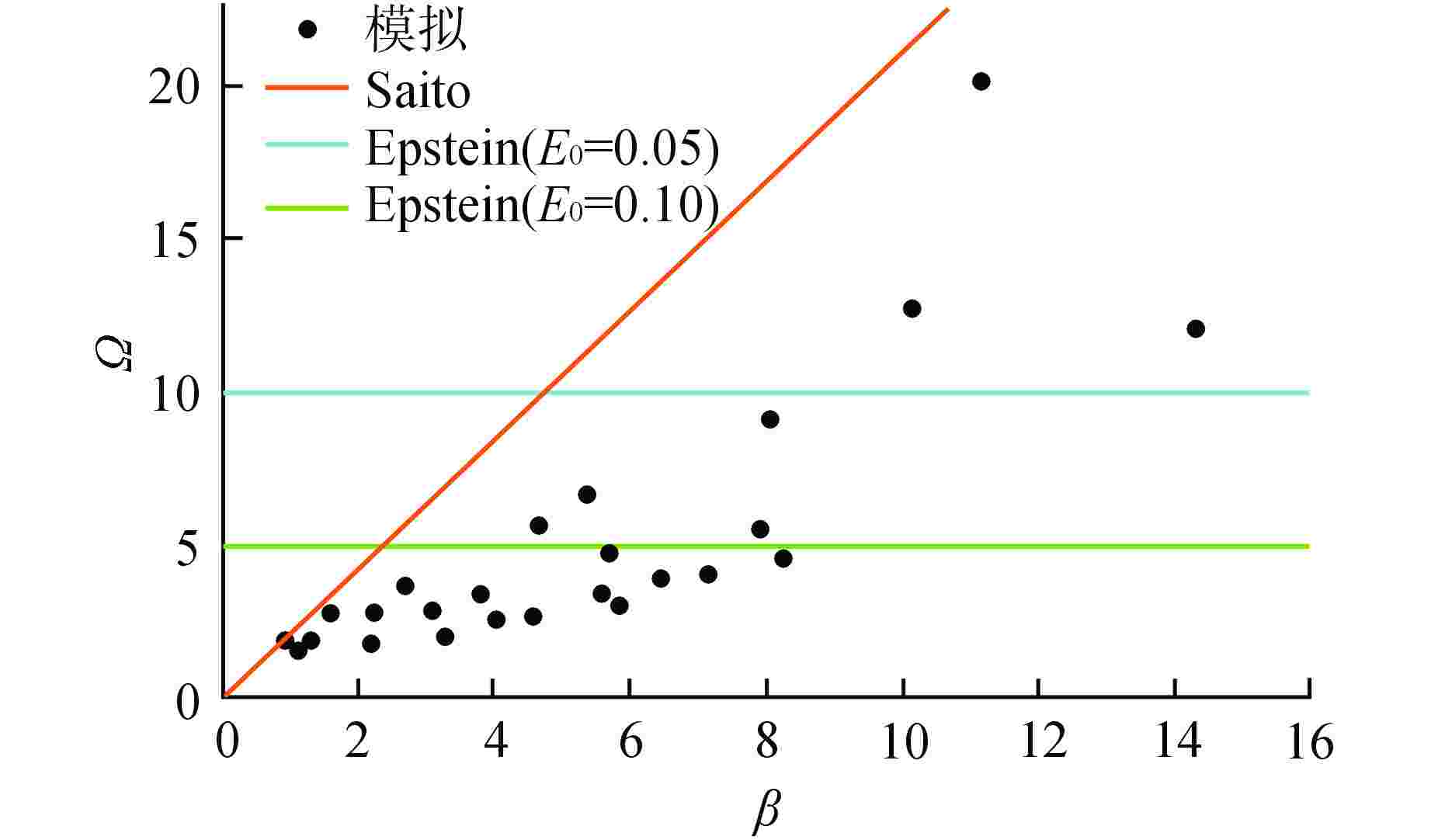
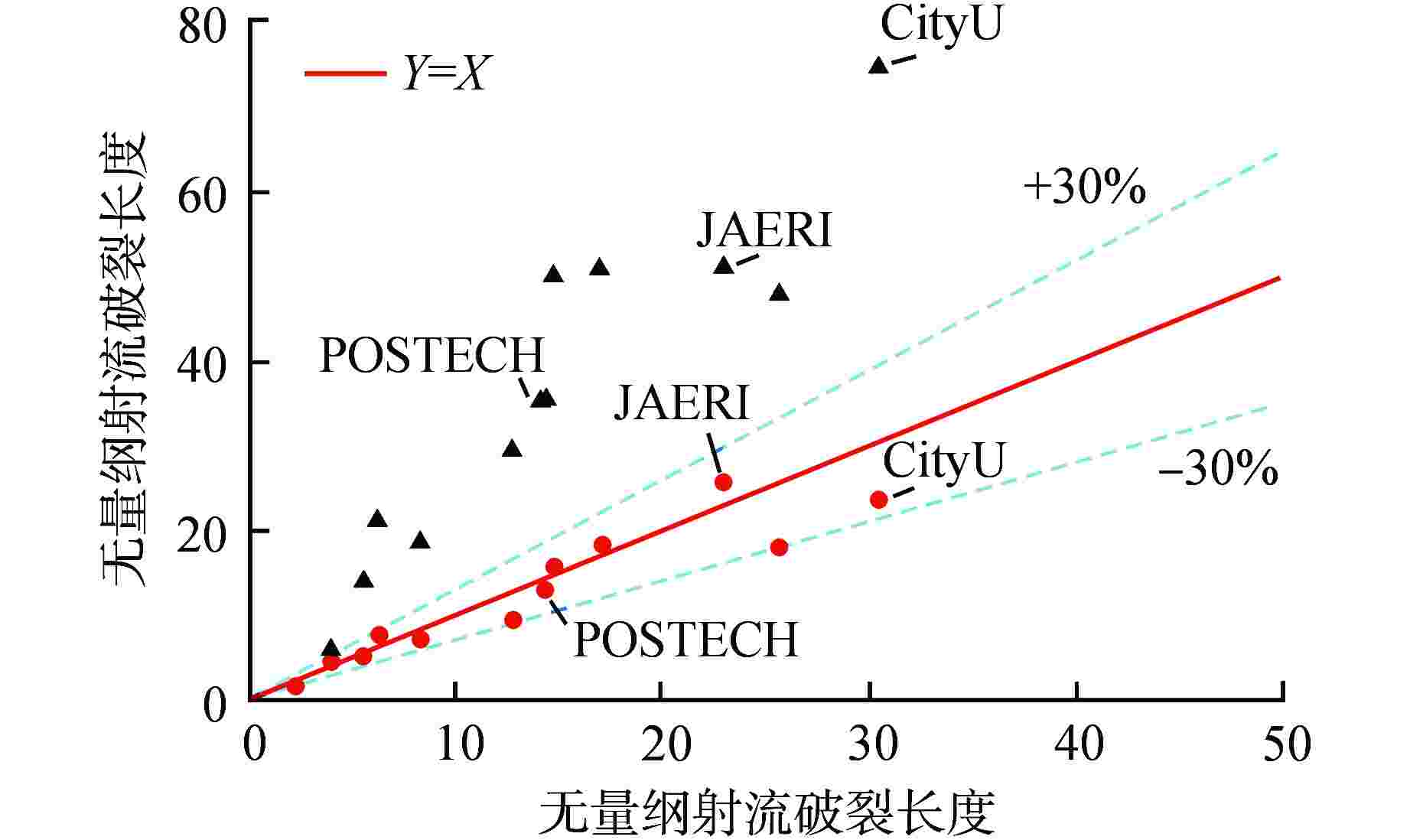
图 4 模拟数据与先前经验关系式的对比
$ \varOmega = {{\left( {{{{L_{{\text{brk}}}}} \mathord{\left/ {\vphantom {{{L_{{\text{brk}}}}} {{D_{{\text{jet}}}}}}} \right. } {{D_{{\text{jet}}}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{L_{{\text{brk}}}}} \mathord{\left/ {\vphantom {{{L_{{\text{brk}}}}} {{D_{{\text{jet}}}}}}} \right. } {{D_{{\text{jet}}}}}}} \right)} {{{\left( {{{{\rho _{{\mathrm{jet}}}}} \mathord{\left/ {\vphantom {{{\rho _{{\mathrm{jet}}}}} {{\rho _{\mathrm{c}}}}}} \right. } {{\rho _{\mathrm{c}}}}}} \right)}^{0.5}}}}} \right. } {{{\left( {{{{\rho _{{\mathrm{jet}}}}} \mathord{\left/ {\vphantom {{{\rho _{{\mathrm{jet}}}}} {{\rho _{\mathrm{c}}}}}} \right. } {{\rho _{\mathrm{c}}}}}} \right)}^{0.5}}}} \text{；} \beta = {\left( {{{V_{{\mathrm{jet}}}^2} \mathord{\left/ {\vphantom {{{V_{{\mathrm{jet}}}}^2} {g{D_{{\mathrm{jet}}}}}}} \right. } {g{D_{{\mathrm{jet}}}}}}} \right)^{0.5}} $
Figure 4. Comparison of Simulated Data with Previous Empirical Correlations
表 1 参考实验的材料物性参数
Table 1. Physical Parameters of Materials for Reference Experiment
参数 伍德合金 水 二氧化铀 钠 密度/(kg·m−3) 9400 1000 8756 856 参考温度/K 473.15 293.15 3273.15 673.15 表面张力/(N·m−1) 0.430 0.072 0.484 0.179 运动粘度/(m2·s−1) 2.95×10−7 1.09×10−6 7.41×10−7 3.24×10−7 射流与冷却剂的密度比 9.4 10.1 
下载: 导出CSV
表 2 数值模拟的材料物性参数
Table 2. Physical Parameters of Materials for Numerical Simulation
实验材料 密度/
(kg·m−3)参考温
度/K运动粘度/
(m2·s−1)表面张力/
(N·m−1)原型材料
（UO2∶ZrO2=80%∶20%）7960 3273.15 5.65×10−7 0.450 二氧化铀 8756 3273.15 7.41×10−7 0.484 苯甲酸苄酯 1118 293.15 7.56×10−6 0.044 汞 13600 293.15 1.14×10−7 0.510 伍德合金 9400 493.15 2.95×10−7 0.430 水 1000 293.15 1.09×10−6 0.072
下载: 导出CSV
表 3 研究因素和水平
Table 3. Research Factors and Levels
密度比（因素A） 速度（ 因素 B）/(m·s−1) 直径（因素 C）/mm 1(8.0) ① 1(0.5) 1(10.0) 2(1.1) 2(1.2) 2(20.0) 3(13.6) 3(2.5) 3(15.0) 4(8.8) 4(3.2) 4(5.0) 5(9.4) 5(1.8) 5(30.0) 注：① 1(8.0)表示水平数为1，密度比为8.0，下同
下载: 导出CSV
表 4 L25(56)正交实验结果
Table 4. Results of L25(56) Orthogonal Experiments
密度比
（因素A）速度（因素B）/
(m·s−1)直径（因素C）/
mmD E F 射流破
裂长度/m1(8.0) 1(0.5) 1(10) 1 1 1 0.080 1(8.0) 2(1.2) 3(15) 4 5 2 0.122 1(8.0) 3(2.5) 5(30) 2 4 3 0.228 1(8.0) 4(3.2) 2(20) 5 3 4 0.230 1(8.0) 5(1.8) 4(5) 3 2 5 0.128 2(1.1) 1(0.5) 5(30) 4 3 5 0.062 2(1.1) 2(1.2) 2(20) 2 2 1 0.078 2(1.1) 3(2.5) 4(5) 5 1 2 0.107 2(1.1) 4(3.2) 1(10) 3 5 3 0.135 2(1.1) 5(1.8) 3(15) 1 4 4 0.090 3(13.6) 1(0.5) 4(5) 2 5 4 0.052 3(13.6) 2(1.2) 1(10) 5 4 5 0.126 3(13.6) 3(2.5) 3(15) 3 3 1 0.219 3(13.6) 4(3.2) 5(30) 1 2 2 0.338 3(13.6) 5(1.8) 2(20) 4 1 3 0.190 4(8.8) 1(0.5) 3(15) 5 2 3 0.085 4(8.8) 2(1.2) 5(30) 3 1 4 0.161 4(8.8) 3(2.5) 2(20) 1 5 5 0.202 4(8.8) 4(3.2) 4(5) 4 4 1 0.179 4(8.8) 5(1.8) 1(10) 2 3 2 0.142 5(9.4) 1(0.5) 2(20) 3 4 2 0.095 5(9.4) 2(1.2) 4(5) 1 3 3 0.103 5(9.4) 3(2.5) 1(10) 4 2 4 0.170 5(9.4) 4(3.2) 3(15) 2 1 5 0.214 5(9.4) 5(1.8) 5(30) 5 5 1 0.185
下载: 导出CSV
表 5 正交实验结果的极差分析
Table 5. Polar Analysis of Results of Orthogonal Experiments
项目 密度比
（因素A）射流速度（因素B）/
(m·s−1)射流直径
（因素C）/mmD E F K1 0.788 0.374 0.653 0.813 0.752 0.741 K2 0.472 0.590 0.795 0.714 0.799 0.804 K3 0.925 0.926 0.730 0.738 0.756 0.741 K4 0.769 1.096 0.569 0.723 0.718 0.703 K5 0.767 0.735 0.974 0.733 0.696 0.732 R 0.453 0.722 0.405 0.099 0.103 0.101
下载: 导出CSV
表 6 正交实验结果的方差分析
Table 6. Variance Analysis of Results of Orthogonal Experiments
方差来源 离差平方和 自由度 均方 统计量 显著性 A 0.0220 4 0.0055 18.39 ** B 0.0635 4 0.0159 53.21 ** C 0.0189 4 0.0047 15.84 ** 误差 0.0036 12 0.0003
下载: 导出CSV
表 7 拟合组数据
Table 7. Fitting Group Data
密度比
（因素A）速度（因素B）/
(m·s−1)直径（因素C）/mm 射流破裂
长度/m1(8.0) 1(0.5) 1(10) 0.080 1(8.0) 3(2.5) 5(30) 0.228 1(8.0) 4(3.2) 2(20) 0.230 2(1.1) 3(2.5) 4(5) 0.107 2(1.1) 4(3.2) 1(10) 0.135 2(1.1) 5(1.8) 3(15) 0.090 3(13.6) 1(0.5) 4(5) 0.052 3(13.6) 4(3.2) 5(30) 0.338 3(13.6) 5(1.8) 2(20) 0.190 4(8.8) 1(0.5) 3(15) 0.085 4(8.8) 3(2.5) 2(20) 0.202 4(8.8) 4(3.2) 4(5) 0.179 5(9.4) 1(0.5) 2(20) 0.095 5(9.4) 2(1.2) 4(5) 0.103 5(9.4) 4(3.2) 3(15) 0.214
下载: 导出CSV
表 8 验证组数据
Table 8. Validation Group Data
密度比
（因素A）速度（因素B）/
(m·s−1)直径（因素C）/mm 射流破裂
长度/m1(8.0) 2(1.2) 3(15) 0.122 1(8.0) 5(1.8) 4(5) 0.128 2(1.1) 1(0.5) 5(30) 0.062 2(1.1) 2(1.2) 2(20) 0.078 3(13.6) 2(1.2) 1(10) 0.126 3(13.6) 3(2.5) 3(15) 0.219 4(8.8) 2(1.2) 5(30) 0.161 4(8.8) 5(1.8) 1(10) 0.142 5(9.4) 3(2.5) 1(10) 0.170 5(9.4) 5(1.8) 5(30) 0.185
下载: 导出CSV
表 9 参考实验信息
Table 9. Reference Experiment Information
研究机构 实验材料 密度比 速度/
（m·s−1）射流直
径/mm射流破裂
长度/mCityU 汞/水 13.6 2.16 5 0.152 POSTECH 伍德合金/水 8.8 3.35 35 0.490 JAERI ZAO/水① 3.4 7.80 35 0.800 注：①ZAO为ZrO2-Al2O3(49%∶51%)合金
下载: 导出CSV
-
[1] THEOFANOUS T G, SAITO M. An assessment of Class-9 (core-melt) accidents for PWR dry-containment systems[J]. Nuclear Engineering and Design, 1981, 66(3): 301-332. doi: 10.1016/0029-5493(81)90162-X [2] BRAYER C, LE MONNIER A, CHIKHI N. Impact of corium thermophysical properties on fuel-coolant interaction[J]. Annals of Nuclear Energy, 2020, 147: 107613. doi: 10.1016/j.anucene.2020.107613 [3] 彭程,邓坚. 蒸汽夹带作用下高温颗粒表面拖曳力模型研究[J]. 核动力工程,2022, 43(6): 61-65. [4] SUN R Y, WU L P, DING W, et al. From melt jet break-up to debris bed formation: a review of melt evolution model during fuel-coolant interaction[J]. Annals of Nuclear Energy, 2022, 165: 108642. doi: 10.1016/j.anucene.2021.108642 [5] CORRADINI M L, KIM B J, OH M D. Vapor explosions in light water reactors: a review of theory and modeling[J]. Progress in Nuclear Energy, 1988, 22(1): 1-117. doi: 10.1016/0149-1970(88)90004-2 [6] TAYLOR G I. Scientific papers. Vol. Ⅲ: aerodynamics and the mechanics of projectiles and explosions [M]. New York: Cambridge University Press, 1963: 287-303. [7] EPSTEIN M, FAUSKE H K. Applications of the turbulent entrainment assumption to immiscible gas-liquid and liquid-liquid systems[J]. Chemical Engineering Research and Design, 2001, 79(4): 453-462. doi: 10.1205/026387601750282382 [8] MATSUO E, ABE Y, CHITOSE K, et al. Study on jet breakup behavior at core disruptive accident for fast breeder reactor[J]. Nuclear Engineering and Design, 2008, 238(8): 1996-2004. doi: 10.1016/j.nucengdes.2007.11.011 [9] SAITO M, SATO K, IMAHORI S. Experimental study on penetration behaviors of water jet into Freon-11 and liquid nitrogen [C]. Houston: Proceeding of 1988 National Heat Transfer Conference, 1988. [10] KOSHIZUKA S, NOBE A, OKA Y. Numerical analysis of breaking waves using the moving particle semi-implicit method[J]. International Journal for Numerical Methods in Fluids, 1998, 26(7): 751-769. doi: 10.1002/(SICI)1097-0363(19980415)26:7<751::AID-FLD671>3.0.CO;2-C [11] PARK S, PARK H S, JANG B I, et al. 3-D simulation of plunging jet penetration into a denser liquid pool by the RD-MPS method[J]. Nuclear Engineering and Design, 2016, 299: 154-162. doi: 10.1016/j.nucengdes.2015.08.003 [12] CAI Q H, CHEN R H, GUO K L, et al. An enhanced moving particle semi-implicit method for simulation of incompressible fluid flow and fluid-structure interaction[J]. Computers & Mathematics with Applications, 2023, 145: 41-57. [13] BRACKBILL J U, KOTHE D B, ZEMACH C. A continuum method for modeling surface tension[J]. Journal of Computational Physics, 1992, 100(2): 335-354. doi: 10.1016/0021-9991(92)90240-Y [14] DING W, XIAO X K, CAI Q H, et al. Numerical investigation of fluid–solid interaction during debris bed formation based on MPS-DEM[J]. Annals of Nuclear Energy, 2022, 175: 109244. doi: 10.1016/j.anucene.2022.109244 [15] TIAN W X, QIU S Z, SUI G H, et al. Numerical solution on spherical vacuum bubble collapse using MPS method[J]. Journal of Engineering for Gas Turbines and Power, 2010, 132(10): 102920. doi: 10.1115/1.4001058 [16] CHEN R H, CAI Q H, ZHANG P H, et al. Three-dimensional numerical simulation of the HECLA-4 transient MCCI experiment by improved MPS method[J]. Nuclear Engineering and Design, 2019, 347: 95-107. doi: 10.1016/j.nucengdes.2019.03.024 [17] CAI Q H, ZHU D H, CHEN R H, et al. Three-dimensional numerical study on the effect of sidewall crust thermal resistance on transient MCCI by improved MPS method[J]. Annals of Nuclear Energy, 2020, 144: 107525. doi: 10.1016/j.anucene.2020.107525 [18] 陈荣华, 田文喜, 左娟莉, 等. 基于MPS方法的液态铅铋合金内气泡上升流数值模拟[J]. 核动力工程,2011,32(5): 96-99.陈荣华, 田文喜, 左娟莉, 等. 基于MPS方法的液态铅铋合金内气泡上升流数值模拟[J]. 核动力工程, 2011,32(5): 96-99. [19] MEIGNEN R, RAVERDY B, PICCHI S, et al. The challenge of modeling fuel-coolant interaction: Part II -Steam explosion[J]. Nuclear Engineering and Design, 2014, 280: 528-541. doi: 10.1016/j.nucengdes.2014.08.028 [20] CHENG H, ZHAO J Y, WANG J. Experimental investigation on the characteristics of melt jet breakup in water: the importance of surface tension and Rayleigh-Plateau instability[J]. International Journal of Heat and Mass Transfer, 2019, 132: 388-393. doi: 10.1016/j.ijheatmasstransfer.2018.12.026 [21] NISHIMURA S, SUGIYAMA K I, KINOSHITA I, et al. Fragmentation mechanisms of a single molten copper jet penetrating a sodium pool-transition from thermal to hydrodynamic fragmentation in instantaneous contact interface temperatures below its freezing point[J]. Journal of Nuclear Science and Technology, 2010, 47(3): 219-228. doi: 10.1080/18811248.2010.9711948 [22] CHU C C, SIENICKI J J, SPENCER B W, et al. Ex-vessel melt-coolant interactions in deep water pool: studies and accident management for Swedish BWRs[J]. Nuclear Engineering and Design, 1995, 155(1-2): 159-213. doi: 10.1016/0029-5493(94)00874-X [23] DINH T N, BUI V A, NOURGALIEV R R, et al. Experimental and analytical studies of melt jet-coolant interactions: a synthesis[J]. Nuclear Engineering and Design, 1999, 189(1-3): 299-327. doi: 10.1016/S0029-5493(98)00275-1 [24] THAKRE S, MANICKAM L, MA W M. A numerical simulation of jet breakup in melt coolant interactions[J]. Annals of Nuclear Energy, 2015, 80: 467-475. doi: 10.1016/j.anucene.2015.02.038 [25] 李云雁,胡传荣. 试验设计与数据处理[M]. 第三版. 北京: 化学工业出版社,2017: 68-75. [26] CHEN J T, ZHOU Y, ZHAO J Y, et al. Experimental and theoretical study of jet hydrodynamic breakup behavior with air entrainment[J]. Annals of Nuclear Energy, 2021, 151: 107900. doi: 10.1016/j.anucene.2020.107900 [27] JUNG W H, PARK H S, MORIYAMA K, et al. Analysis of experimental uncertainties in jet breakup length and jet diameter during molten fuel-coolant interaction[J]. Nuclear Engineering and Design, 2019, 344: 183-194. doi: 10.1016/j.nucengdes.2019.01.018 [28] MORIYAMA K, MARUYAMA Y, USAMI T, et al. Coarse break-up of a stream of oxide and steel melt in a water pool: JAERI-Research-2005-017[R]. Kashiwa: Japan Atomic Energy Research Institute, 2005. -
计量
- 文章访问数: 37
- HTML全文浏览量: 10
- PDF下载量: 14
- 被引次数: 0
