非结构网格变分节块法在氦氙冷却小型反应堆中的应用

孙启政; 刘晓晶; 张滕飞

doi:10.13832/j.jnpe.2024.05.0026

非结构网格变分节块法在氦氙冷却小型反应堆中的应用

doi: 10.13832/j.jnpe.2024.05.0026

上海交通大学核科学与工程学院，上海，200240

基金项目: 国家重点研发计划（2020YFB1901900）；国家自然科学基金面上项目（12175138）

详细信息

作者简介:
孙启政（1997—），男，博士研究生，现主要从事中子输运算法相关研究，E-mail: qizhengsun@sjtu.edu.cn

通讯作者:
张滕飞，E-mail: zhangtengfei@sjtu.edu.cn

中图分类号: TL329
计量
- 文章访问数: 27
- HTML全文浏览量: 8
- PDF下载量: 15
- 被引次数: 0
出版历程
- 收稿日期: 2023-10-30
- 修回日期: 2024-01-13
- 刊出日期: 2024-10-14

Application of Unstructured Mesh Variational Nodal Method in He-Xe Cooled Micro Reactor

School of Nuclear Science and Engineering, Shanghai Jiao Tong University, Shanghai, 200240, China

摘要

摘要: 先进小型反应堆设计方案具有复杂的几何结构和较强的中子泄漏特征。为更准确地对复杂几何的先进小型反应堆设计的中子学特性进行分析，本研究提出了一种基于离散纵标（S_N）的非结构网格变分节块法（UVNM-S_N）。UVNM-S_N从二阶偶对称输运方程的泛函形式出发，在空间上采用任意三角形非结构网格以及坐标变换技术，角度上则采用S_N将原方程进行解耦；选取了氦氙（He-Xe）冷却小型反应堆SIMONS作为分析对象，验证了UVNM-S_N在实际应用对象中的性能。计算结果表明，UVNM-S_N在复杂几何的非均匀问题中具有良好的几何适应性以及计算精度，可为先进反应堆数值模拟提供新的计算思路。
- 变分节块法（VNM） /
- 非结构网格 /
- 氦氙冷却小型反应堆 /
- 离散纵标（S_N）
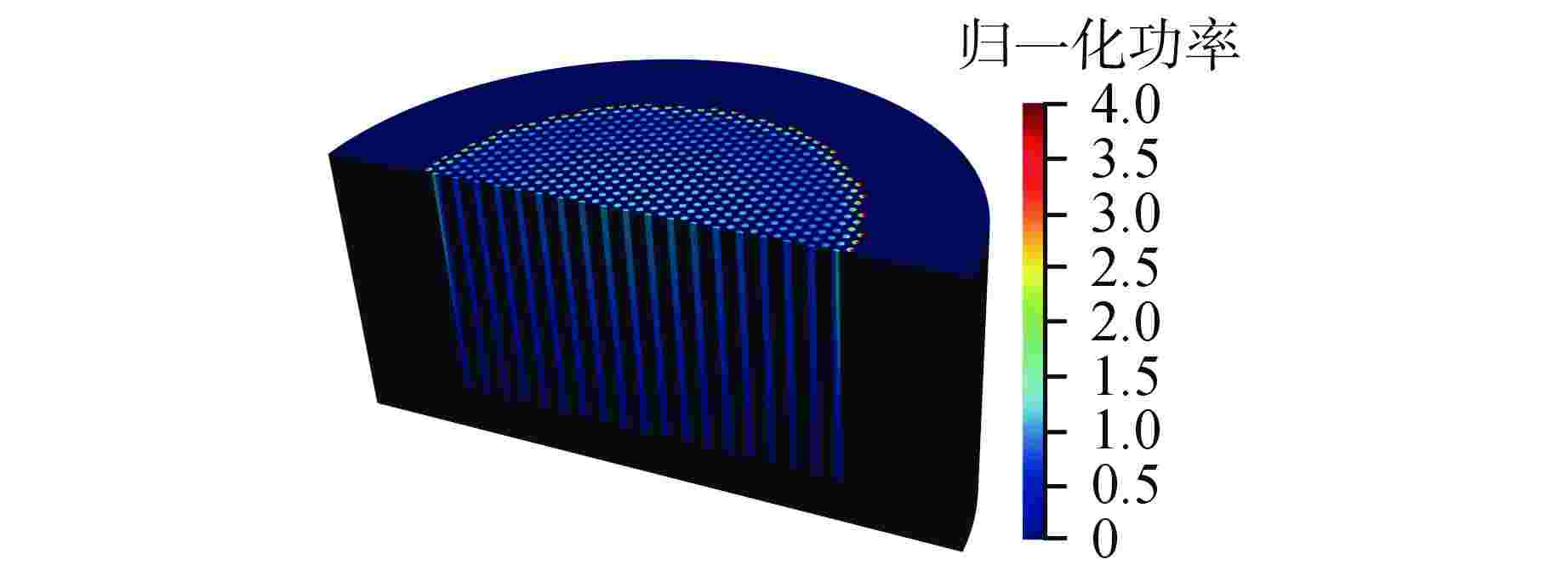
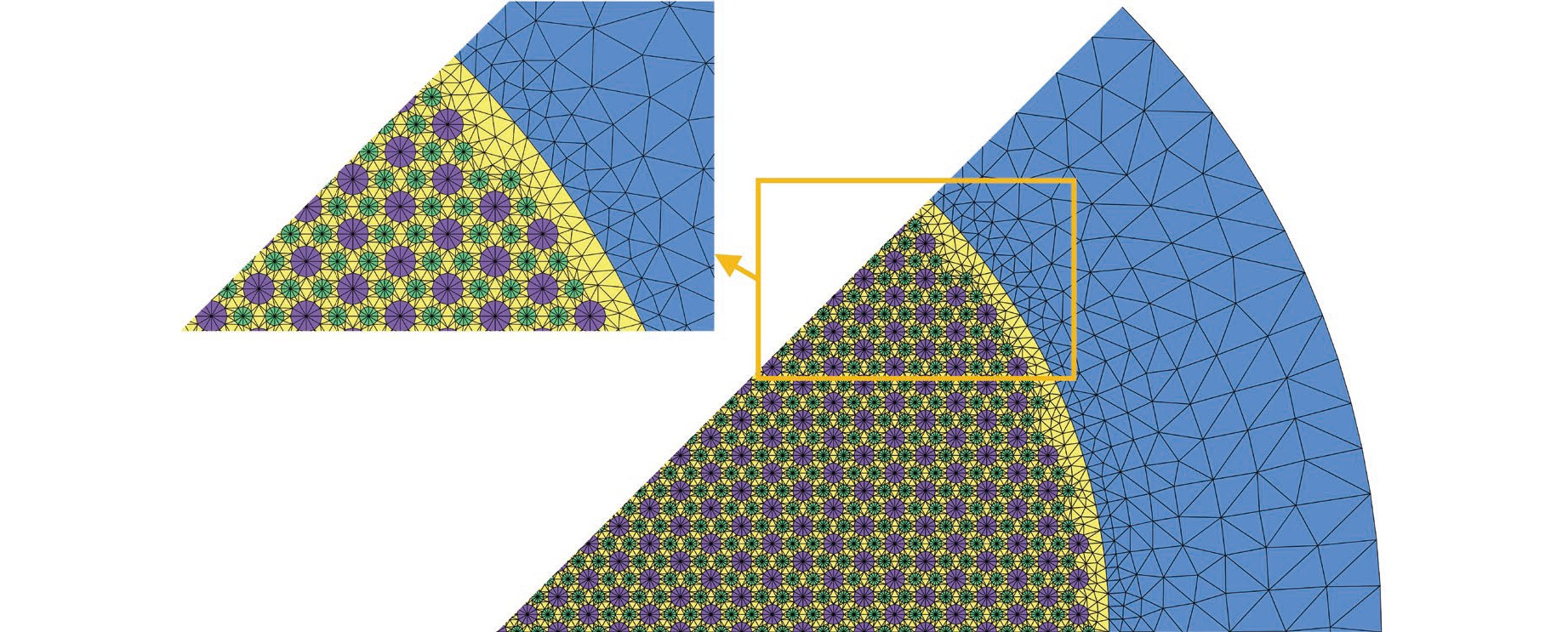
Abstract: Advanced designs of micro reactors are distinguished by intricate geometries and pronounced neutron leakage. To enhance the precision of neutron property analysis in these complex geometrical designs, this study introduces an Unstructured Mesh Variational Nodal Method (UVNM-S_N). The UVNM-S_N method initiates from the functional formulation of the second-order even-parity neutron transport equation. Spatially, arbitrary triangular unstructured meshes and coordinate mapping techniques are employed. Besides, angular decoupling of the original equations is achieved through the application of the discrete-ordinate (S_N) method. Furthermore, the SIMONS design, a helium-xenon (He-Xe)-cooled micro reactor, is chosen as the analytical subject to verify the performance of the UVNM-S_N. Numerical results demonstrate that UVNM-S_N exhibits geometric adaptability and computational precision in heterogeneous problems with complex geometries. Consequently, it is concluded that UVNM-S_N can stand as an innovative strategy for numerical simulations in advanced micro-reactor designs.
- Variational nodal method (VNM) /
- Unstructured mesh /
- He-Xe cooled micro reactor /
- Discrete ordinates method（S_N）

HTML全文

图 1 SIMONS算例八分之一堆芯网格剖分示意图

Figure 1. One-eighth of the Radial Meshes Used for the SIMONS Test Case

下载: 全尺寸图片幻灯片

图 2 SIMONS算例的三维功率分布示意图

Figure 2. Schematic Diagram of 3-D Power Distribution for the SIMONS Test Problem

下载: 全尺寸图片幻灯片

图 3 SIMONS算例归一化相对功率误差分布

Figure 3. Distribution of Normalized Relative Power Error between UVNM-S_N and MGMC for the SIMONS Test Problem

下载: 全尺寸图片幻灯片

图 4 SIMONS算例多群蒙卡功率标准差分布

Figure 4. Standard Deviation Distribution of MGMC Pin Power for the SIMONS Test Problem

下载: 全尺寸图片幻灯片

表 1 SIMONS算例的主要参数

Table 1. Main Parameters of the SIMONS Test Problem

参数名	参数值
燃料棒直径/cm	1.5
He-Xe冷却剂通道直径/cm	0.8
包壳厚度/cm	0.05
燃料-He-Xe冷却剂通道中心距/cm	1.5
燃料棒数目/根	1015
基体半径/cm	45
基体高度/cm	100
径向反射层厚度/cm	20
轴向反射层厚度/cm	10

下载: 导出CSV

表 2 不同数值方法在SIMONS算例中的数值结果

Table 2. Solutions of Different Numerical Methods for the SIMONS Test Problem.

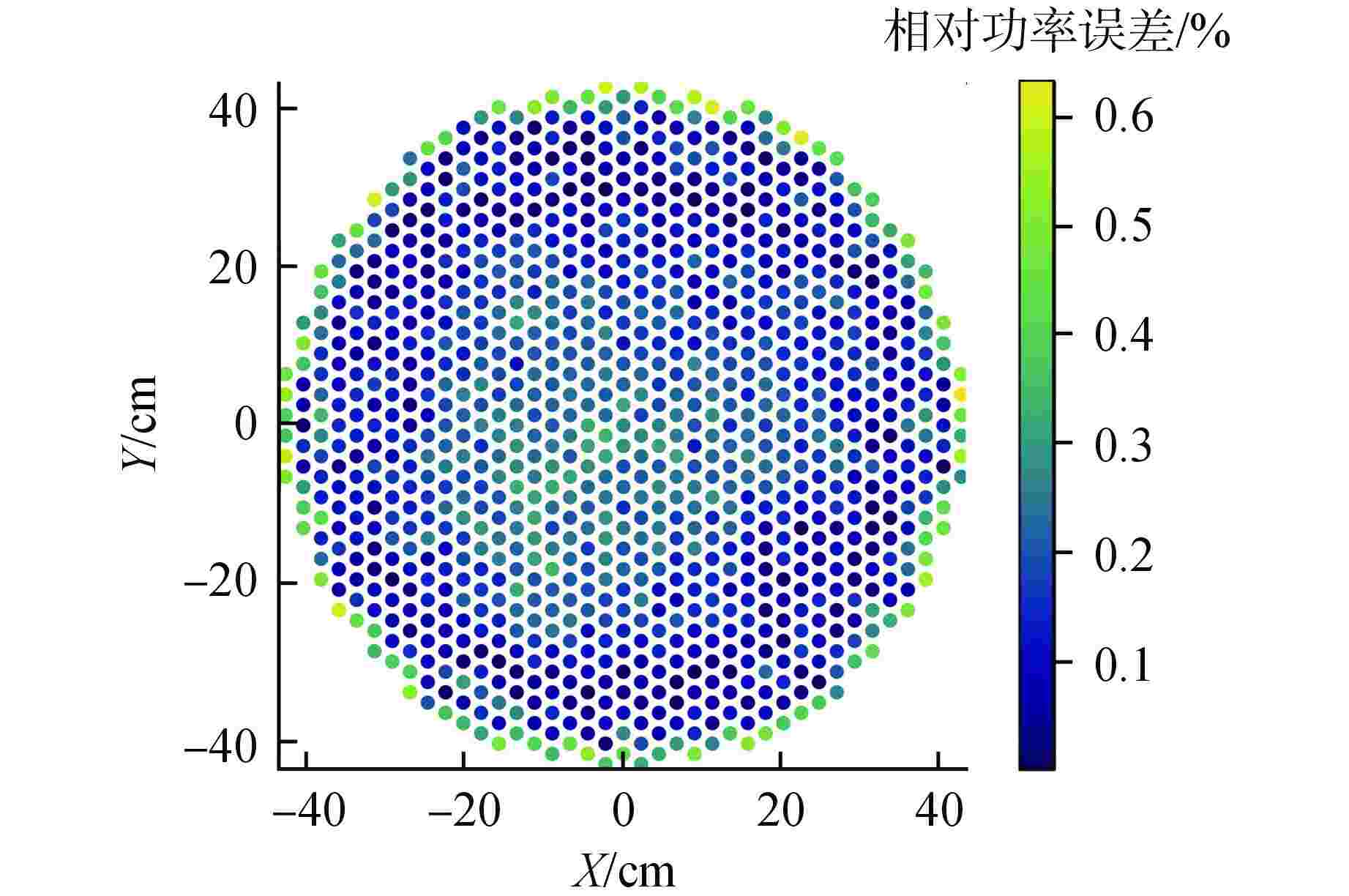
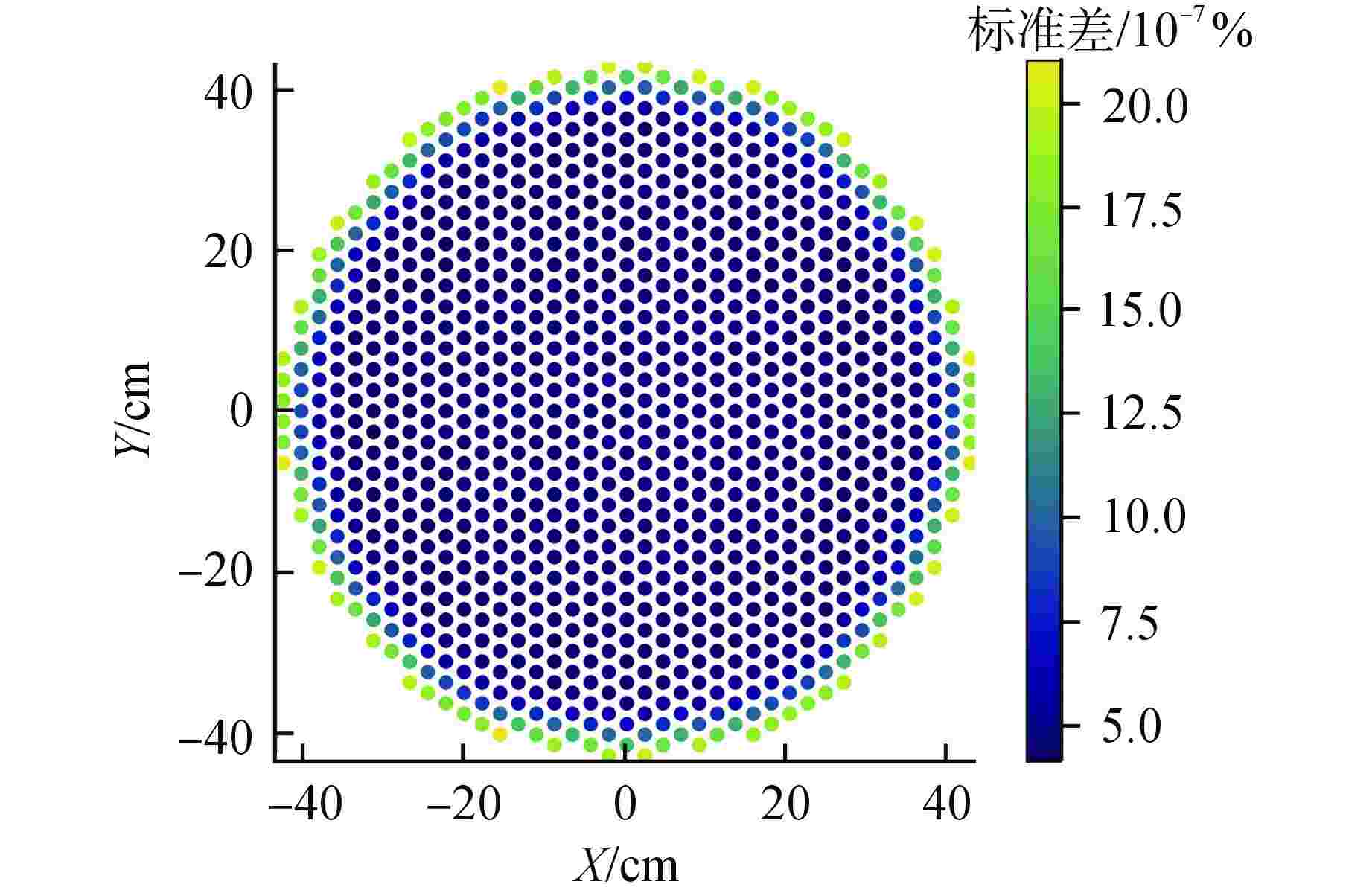
数值方法	多群蒙卡	UVNM-S_N	扩散近似
k_eff	1.15380±0.00002	1.15450	1.12966
k_eff误差/pcm		70	−2414
最大积分棒功率误差/%		0.63	7.20
平均积分棒功率误差/%		0.16	1.72

下载: 导出CSV

参考文献(19)

[1]	STERBENTZ J W, WERNER J E, MCKELLAR M G, et al. Special purpose nuclear reactor (5 MW) for reliable power at remote sites assessment report: INL/EXT-16-40741[R]. Idaho Falls: Idaho National Laboratory, 2017.
[2]	XIAO W, LI X Y, LI P J, et al. High-fidelity multi-physics coupling study on advanced heat pipe reactor[J]. Computer Physics Communications, 2022, 270: 108152. doi: 10.1016/j.cpc.2021.108152
[3]	EKLUND M D, DUPONT M, CARACAPPA P F, et al. Neutronics simulations of the RPI Walthousen Reactor Critical Facility (RCF) using Proteus-SN[J]. Transactions of the American nuclear society, 2017, 117: 114-115.
[4]	WANG Y Q, SCHUNERT S, ORTENSI J, et al. Rattlesnake: a MOOSE-based multiphysics multischeme radiation transport application[J]. Nuclear Technology, 2021, 207(7): 1047-1072. doi: 10.1080/00295450.2020.1843348
[5]	FIORINA C, HURSIN M, PAUTZ A. Extension of the GeN-Foam neutronic solver to SP₃ analysis and application to the CROCUS experimental reactor[J]. Annals of Nuclear Energy, 2017, 101: 419-428. doi: 10.1016/j.anucene.2016.11.042
[6]	JARETEG K, VINAI P, SASIC S, et al. Coupled fine-mesh neutronics and thermal-hydraulics – modeling and implementation for PWR fuel assemblies[J]. Annals of Nuclear Energy, 2015, 84: 244-257. doi: 10.1016/j.anucene.2015.01.037
[7]	WANG J P, MARTIN W R, DOWNAR T J, et al. Code verification and solution verification framework in pin-resolved neutron transport code MPACT[J]. Annals of Nuclear Energy, 2022, 178: 109365. doi: 10.1016/j.anucene.2022.109365
[8]	HSIEH A, ZHANG G C, YANG W S. Consistent transport transient solvers of the high-fidelity transport code PROTEUS-MOC[J]. Nuclear Science and Engineering, 2020, 194(7): 508-540. doi: 10.1080/00295639.2020.1746619
[9]	CHEN J, LIU Z Y, ZHAO C, et al. A new high-fidelity neutronics code NECP-X[J]. Annals of Nuclear Energy, 2018, 116: 417-428. doi: 10.1016/j.anucene.2018.02.049
[10]	ZHAO C, PENG X J, ZHANG H B, et al. A new numerical nuclear reactor neutronics code SHARK[J]. Frontiers in Energy Research, 2021, 9: 784247. doi: 10.3389/fenrg.2021.784247
[11]	ZHANG T F, LI Z P. Variational nodal methods for neutron transport: 40 years in review[J]. Nuclear Engineering and Technology, 2022, 54(9): 3181-3204. doi: 10.1016/j.net.2022.04.012
[12]	SMITH M A, TSOULFANIDIS N, LEWIS E E, et al. A finite subelement generalization of the variational nodal method[J]. Nuclear Science and Engineering, 2003, 144(1): 36-46. doi: 10.13182/NSE144-36
[13]	ZHANG T F, WANG Y P, LEWIS E E, et al. A three-dimensional variational nodal method for pin-resolved neutron transport analysis of pressurized water reactors[J]. Nuclear Science and Engineering, 2017, 188(2): 160-174. doi: 10.1080/00295639.2017.1350002
[14]	ZHANG T F, LEWIS E E, SMITH M A, et al. A variational nodal approach to 2D/1D pin resolved neutron transport for pressurized water reactors[J]. Nuclear Science and Engineering, 2017, 186(2): 120-133. doi: 10.1080/00295639.2016.1273023
[15]	WANG Y Q, RABITI C, PALMIOTTI G. Krylov solvers preconditioned with the low-order red-black algorithm for the PN hybrid FEM for the INSTANT code[C]//Proceedings of the International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering (M&C 2011). Rio de Janeiro, RJ, Brazil: CD-ROM, Latin American Section (LAS), American Nuclear Society (ANS), 2011.
[16]	LI X Y, LIU X J, CHAI X, et al. Multi-physics coupling simulation of small mobile nuclear reactor with finite element-based models[J]. Computer Physics Communications, 2023, 293: 108900. doi: 10.1016/j.cpc.2023.108900
[17]	ROMANO P K, HORELIK N E, HERMAN B R, et al. OpenMC: a state-of-the-art Monte Carlo code for research and development[J]. Annals of Nuclear Energy, 2015, 82: 90-97. doi: 10.1016/j.anucene.2014.07.048
[18]	GEUZAINE C, REMACLE J F. Gmsh: a 3-D finite element mesh generator with built-in pre-and post-processing facilities[J]. International Journal for Numerical Methods in Engineering, 2009, 79(11): 1309-1331. doi: 10.1002/nme.2579
[19]	SUN Q Z, XIAO W, LI X Y, et al. A variational nodal formulation for multi-dimensional unstructured neutron diffusion problems[J]. Nuclear Engineering and Technology, 2023, 55(6): 2172-2194. doi: 10.1016/j.net.2023.02.021