Study on Treatment Method of Environmental Effect of Hexagonal Assembly PWR
-
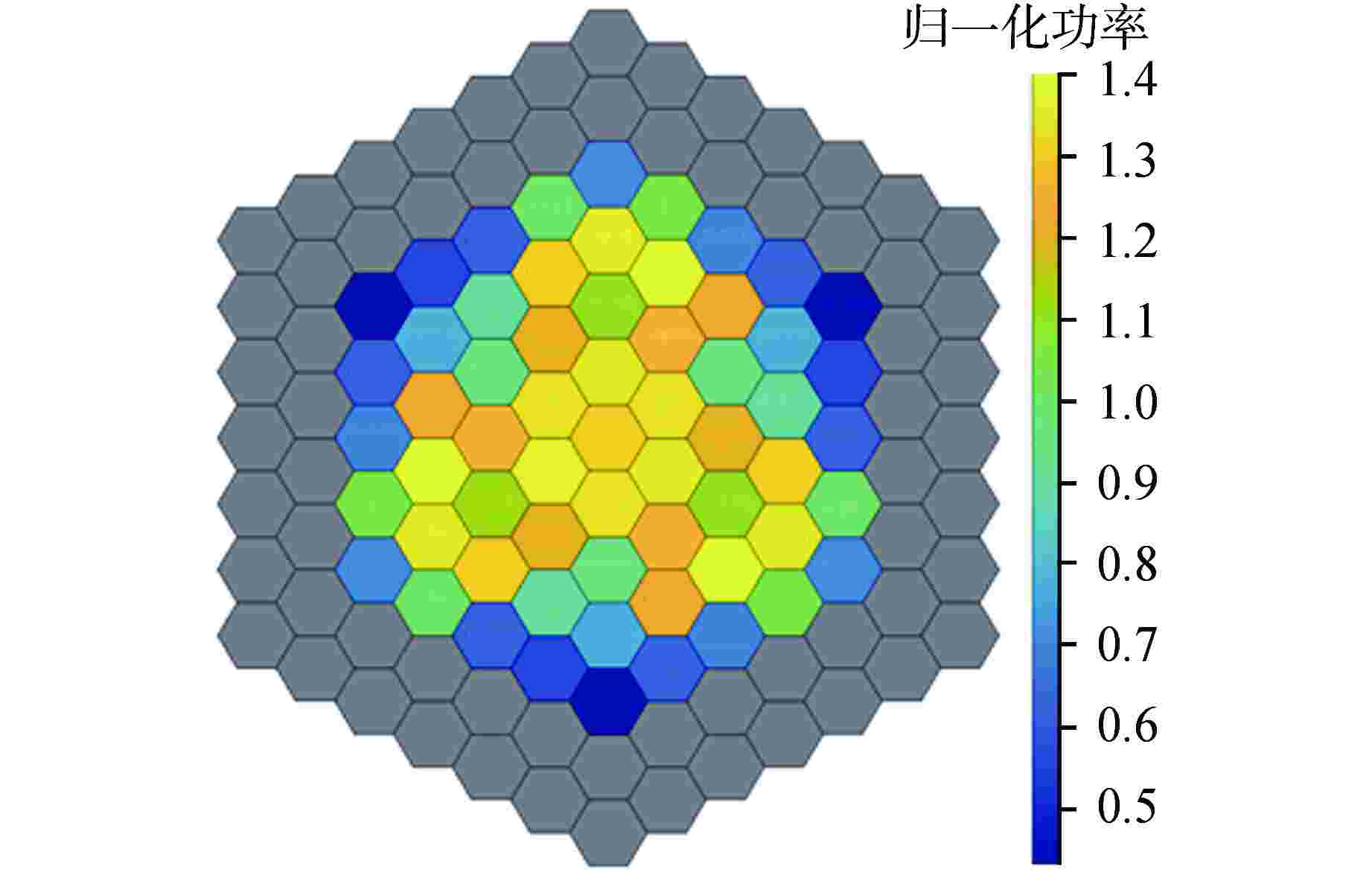
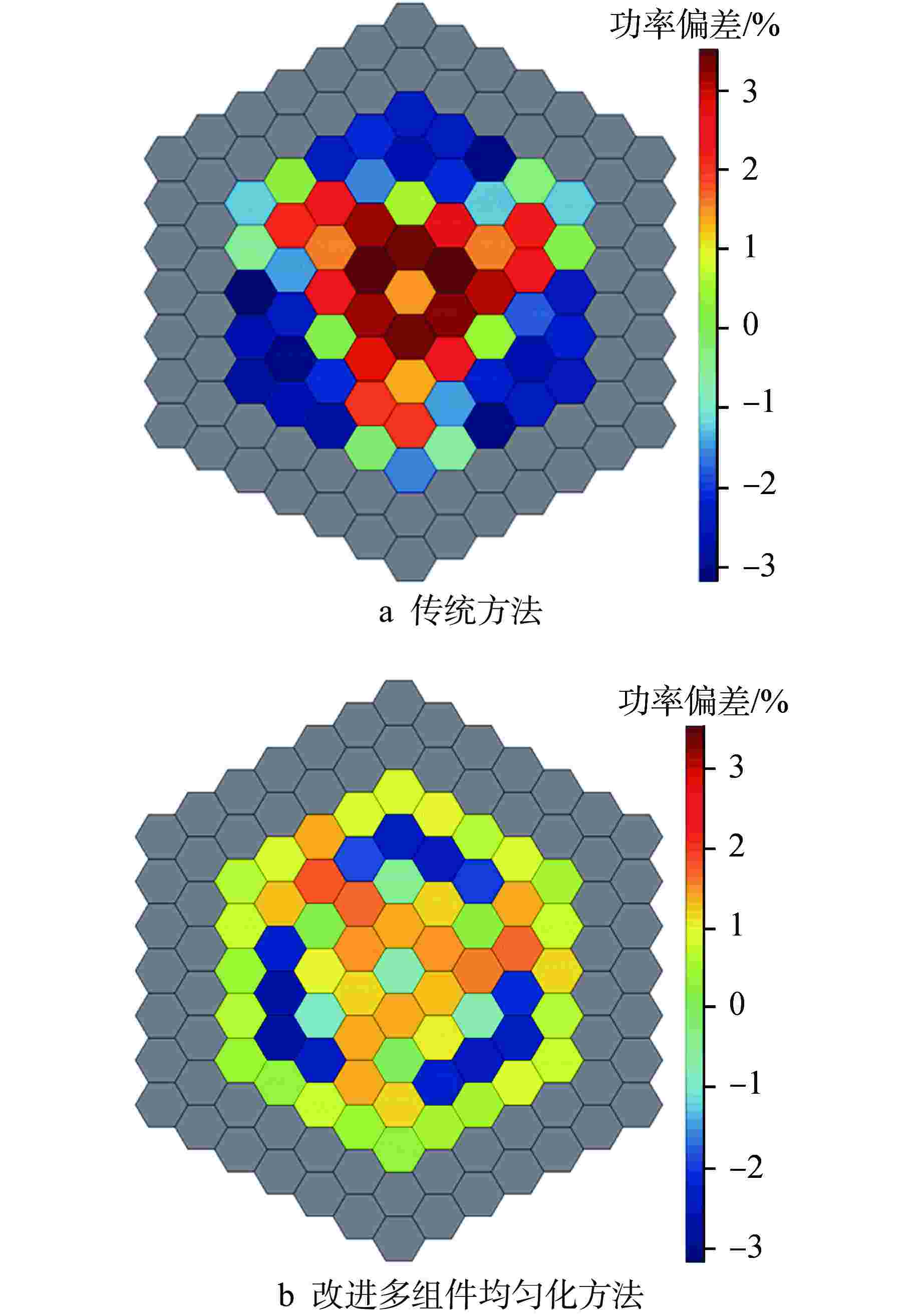
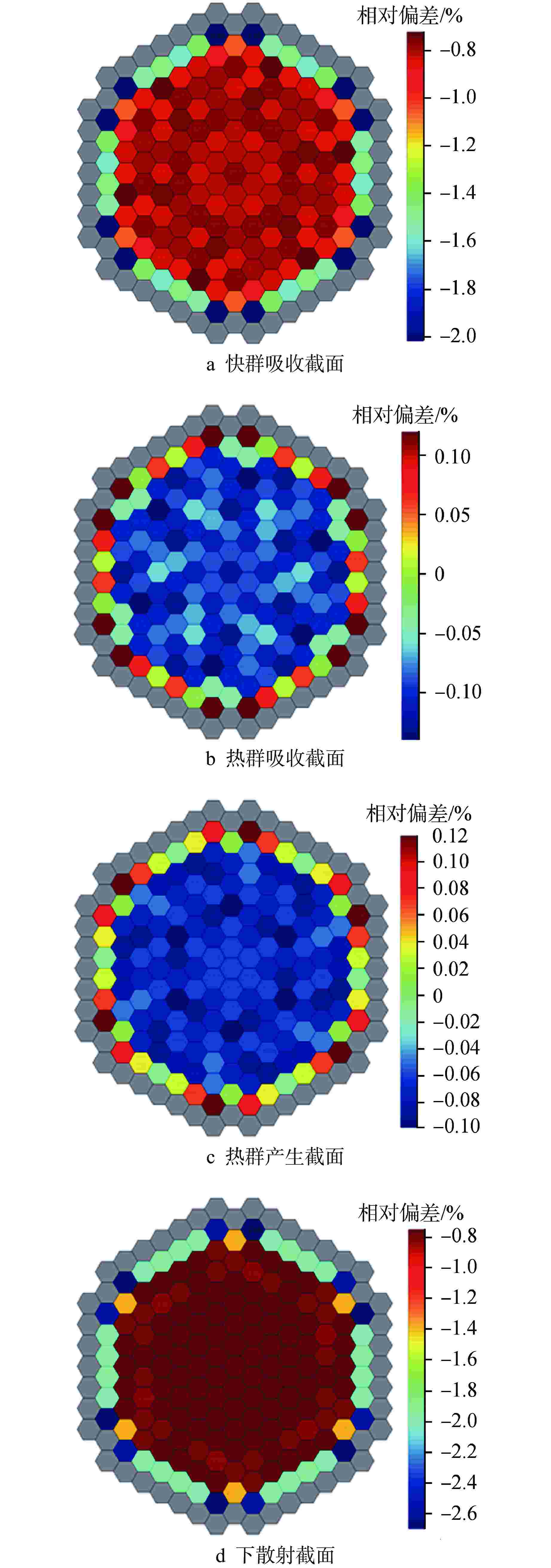
摘要: 针对六角形组件压水堆，提出一种改进多组件均匀化方法，以降低燃料组件环境效应对两步法计算精度的影响，并从燃耗深度这一状态变量出发，开展了敏感性分析，拓展了该方法的实用性。该方法通过构建多组件模型近似获取毗邻反射层燃料组件的真实堆芯能谱，采用非均匀修正因子减少由于环境效应对单组件全反射边界模型少群常数计算的偏差，同时仅对传统两步法计算策略进行微调，对整体程序框架影响较小。计算结果表明，该方法可有效改善传统两步法的计算精度，特征值偏差由−341pcm（1pcm=10−5）降低至−111pcm，组件功率均方根偏差也由2.28%减小到1.38%。
-
关键词:
- 六角形组件压水堆 /
- 环境效应 /
- 改进多组件均匀化 /
- NECP-Bamboo-H
Abstract: An improved multi-assembly homogenization method is raised to deal with the environmental effect of the hexagonal fuel assembly in PWRs. In order to reduce the influence of environmental effect of fuel assembly on the calculation accuracy of two-step method, sensitivity analysis is carried out from the state variable of burnup depth, which expands the practicability of this method. In this method, the real core energy spectrum of the fuel assembly adjacent to the reflector is approximately obtained by establishing a multi-assembly model, and the heterogeneous correction factor is adopted to reduce the deviation of the calculation of few-group constants of the single-assembly model with reflective boundary due to environmental effects. At the same time, the traditional two-step calculation strategy is fine-tuned, which has little impact on the overall code framework. The calculation results show that this method can effectively improve the calculation accuracy of the traditional two-step method, and the eigenvalue deviation is reduced from −341pcm (1pcm=10−5) to −111pcm, and the root mean square deviation of assembly power is also reduced from 2.28% to 1.38%. -
图 2 基于二维模型的不连续因子求解流程示意图
Figure 2. Flow Chart of the Solution of DFs Based on 2-D Model
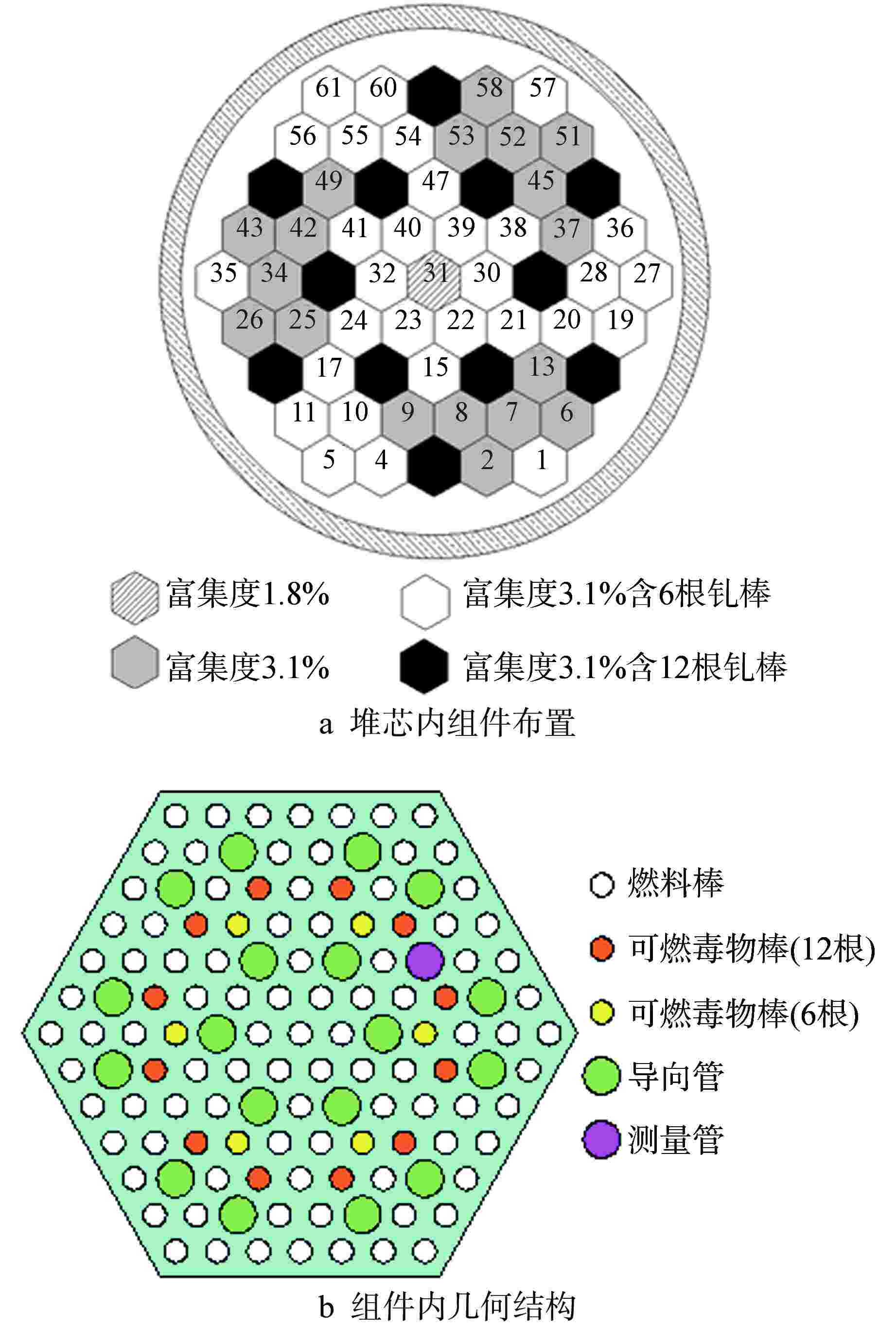
表 1 CAREM-25堆芯参数
Table 1. CAREM-25 Core Parameters
参数名 参数值 热功率/MW 100 燃料富集度/% 1.8~3.1 堆芯内燃料组件总数 61 组件对边距/mm 160 燃料棒中心距/mm 13.8 燃料棒直径/mm 7.6 燃料棒气隙宽度/mm 0.075 燃料棒包壳厚度/mm 0.625 燃料芯块材料 UO2/UO2-Gd2O3(8%) 控制棒材料 AISI316L 
下载: 导出CSV
表 2 特征值计算结果
Table 2. Results of Eigenvalue
计算方法 特征值 偏差/pcm 参考解 1.11521±0.00004 传统方法 1.11180 −341 改进多组件均匀化方法 1.11410 −111
下载: 导出CSV
表 3 组件功率分布计算均方根偏差
Table 3. Root Mean Square Biases of Assembly Power Distribution
计算方法 均方根偏差/% 传统方法 2.28 改进多组件均匀化方法 1.38
下载: 导出CSV
表 4 不同计算模式说明
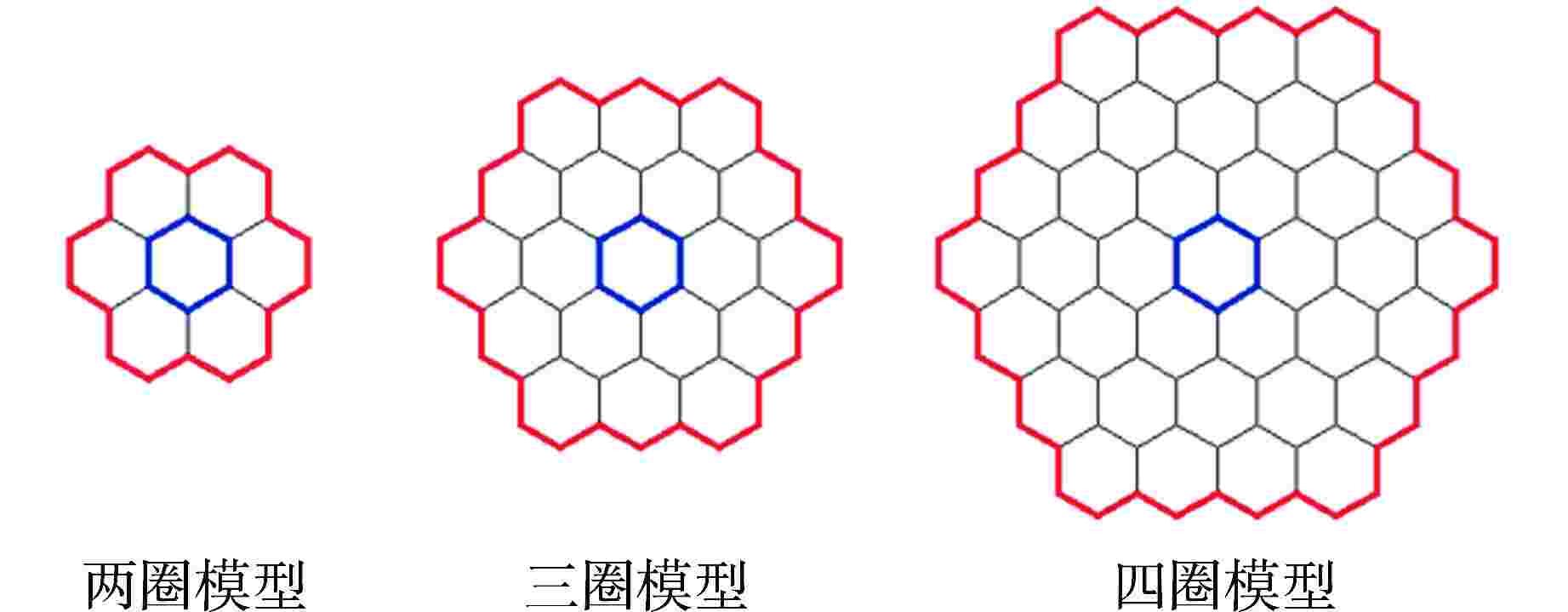
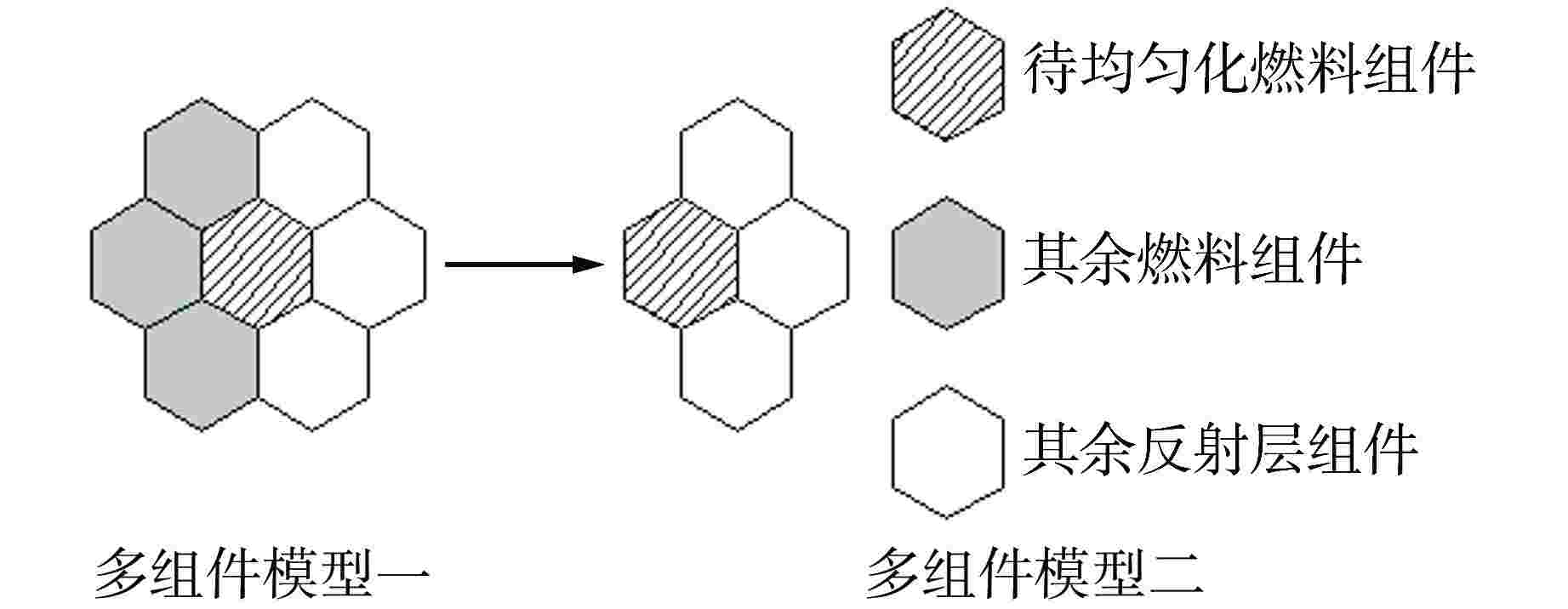
Table 4. Description of Different Calculation Modes
计算模式编号 模型类型 是否考虑修正因子
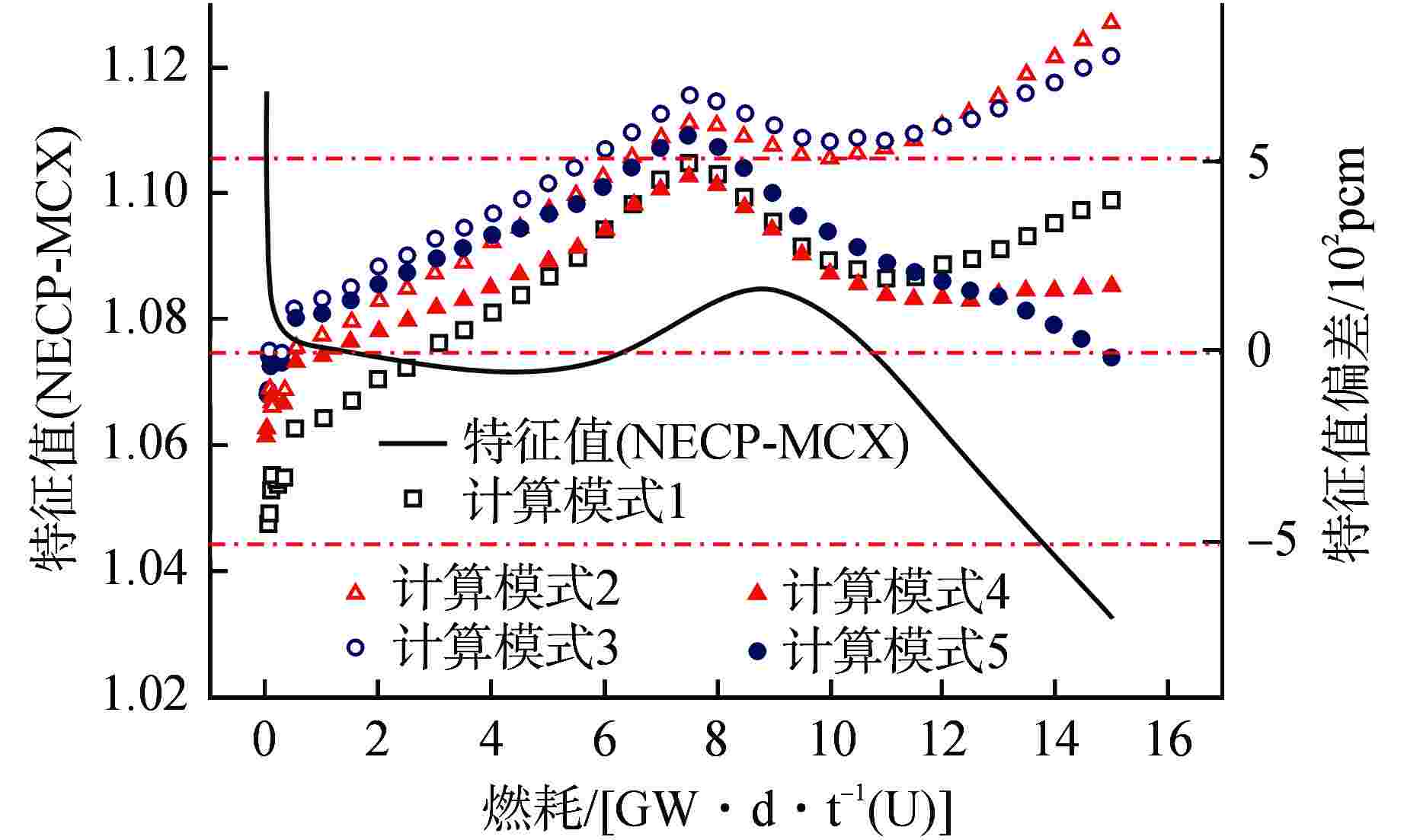
随燃耗的变化1 不采用多组件均匀化方法 2 多组件模型一 否 3 多组件模型二 否 4 多组件模型一 是 5 多组件模型二 是
下载: 导出CSV
表 5 组件功率分布计算偏差统计
Table 5. Summary of Calculation Biases of Assembly Power Distribution
组件功率偏差统计 燃耗深度/[GW·d·t−1(U)] 0 3 6 15 均方根偏差/% 计算模式1 2.282 1.546 1.396 2.609 计算模式2 1.388 1.330 1.592 4.290 计算模式3 1.771 2.476 1.479 3.173 计算模式4 1.393 1.095 1.259 0.725 计算模式5 1.774 1.677 1.872 3.235 最大正偏差/% 计算模式1 3.535 2.402 2.467 4.807 计算模式2 1.811 2.335 3.278 7.817 计算模式3 3.262 2.476 2.166 5.687 计算模式4 1.833 1.556 2.260 1.251 计算模式5 3.275 2.329 2.322 5.085 最小负偏差/% 计算模式1 −3.192 −2.157 −2.115 −5.824 计算模式2 −2.809 −2.194 −2.784 −7.288 计算模式3 −4.344 −4.479 −4.135 −6.433 计算模式4 −2.824 −2.206 −2.151 −3.781 计算模式5 −4.321 −5.130 −5.785 −7.331
下载: 导出CSV
-
[1] KOEBKE K. A new approach to homogenization and group condensation[C]//IAEA Technical Comittee Meeting on Homogenization Methods in Reactor Physics. Lugano, 1978. [2] KOEBKE K. Advances in homogenization and dehomogenization[C]//Proceedings of the International Topical Meeting on Advances in Mathematical Methods for the Solution of Nuclear Engineering Problems. Munich, 1981. [3] YAMAMOTO T. Monte Carlo method with complex weights for neutron leakage-corrected calculations and anisotropic diffusion coefficient generations[J]. Annals of Nuclear Energy, 2012, 50: 141-149. doi: 10.1016/j.anucene.2012.06.025 [4] 汤春桃,黄灏,张少泓. 改进现行轻水堆组件均匀化方法的必要性[J]. 核科学与工程,2007, 27(4): 327-332. doi: 10.3321/j.issn:0258-0918.2007.04.007 [5] 李文淮,刘志宏. 组件均匀化中的边界条件误差修正方法研究[J]. 核科学与工程,2011, 31(3): 199-206. [6] 张斌. 压水堆全堆芯Pin-by-pin均匀化计算方法研究[D]. 西安: 西安交通大学,2017. [7] 汤春桃. 中子输运方程特征线解法及嵌入式组件均匀化方法的研究[D]. 上海: 上海交通大学,2009. [8] SHEN W, ALTIPARMAKOV D. Multicell correction method for treatment of heterogeneities in full-core calculation of CANDU-type Reactors[J]. Nuclear Science and Engineering, 2013, 174(2): 109-134. doi: 10.13182/NSE12-42 [9] BILODID Y, FRIDMAN E, LÖTSCH T. X2 VVER-1000 benchmark revision: Fresh HZP core state and the reference Monte Carlo solution[J]. Annals of Nuclear Energy, 2020, 144: 107558. doi: 10.1016/j.anucene.2020.107558 [10] SMITH K S. Spatial homogenization methods for light water reactor analysis[D]. Cambridge: Massachusetts Institute of Technology, 1980. [11] TAHARA Y, KANAGAWA T, SEKIMOTO H. Two-dimensional baffle/reflector constants for nodal code in PWR core design[J]. Journal of Nuclear Science and Technology, 2000, 37(11): 986-995. doi: 10.1080/18811248.2000.9714982 [12] MITTAG S, PETKOV P T, GRUNDMANN U. Discontinuity factors for non-multiplying material in two-dimensional hexagonal reactor geometry[J]. Annals of Nuclear Energy, 2003, 30(13): 1347-1364. doi: 10.1016/S0306-4549(03)00070-7 [13] 张程. 六角形组件压水堆堆芯物理计算改进方法及其应用[D]. 西安: 西安交通大学,2022. [14] ZHANG C, WAN C H, CAO L Z, et al. Method research and engineering validation of the improved homogenization for the heavy reflector in VVER[J]. Annals of Nuclear Energy, 2022, 173: 109119. doi: 10.1016/j.anucene.2022.109119 [15] LI Y Z, ZHANG B, HE Q M, et al. Development and verification of PWR-core fuel management calculation code system NECP-Bamboo: Part I Bamboo-Lattice[J]. Nuclear Engineering and Design, 2018, 335: 432-440. doi: 10.1016/j.nucengdes.2018.05.030 [16] YANG W, WU H C, LI Y Z, et al. Development and verification of PWR-core fuel management calculation code system NECP-Bamboo: Part II Bamboo-Core[J]. Nuclear Engineering and Design, 2018, 337: 279-290. doi: 10.1016/j.nucengdes.2018.07.017 [17] HE Q M, ZHENG Q, LI J, et al. NECP-MCX: a hybrid Monte-Carlo-Deterministic particle-transport code for the simulation of deep-penetration problems[J]. Annals of Nuclear Energy, 2021, 151: 107978. doi: 10.1016/j.anucene.2020.107978 [18] TASHAKOR S, ZARIFI E, NAMINAZARI M. Neutronic simulation of CAREM-25 small modular reactor[J]. Progress in Nuclear Energy, 2017, 99: 185-195. doi: 10.1016/j.pnucene.2017.05.016 -
图(8) / 表(5)
计量
- 文章访问数: 26
- HTML全文浏览量: 9
- PDF下载量: 7
- 被引次数: 0
