Method Research on Neutron-diffusion Solution Based on Arbitrary Quadrilateral Mesh and Conformal Mapping
-
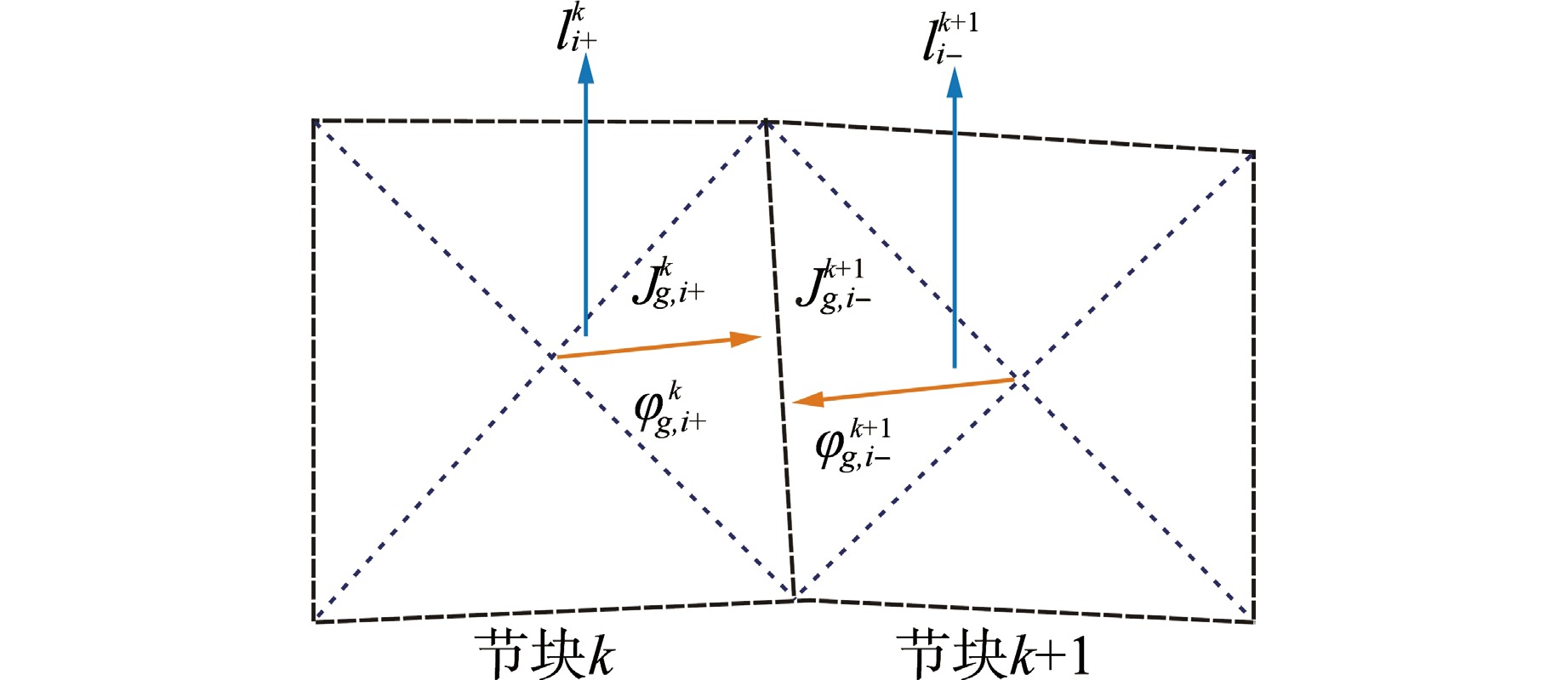
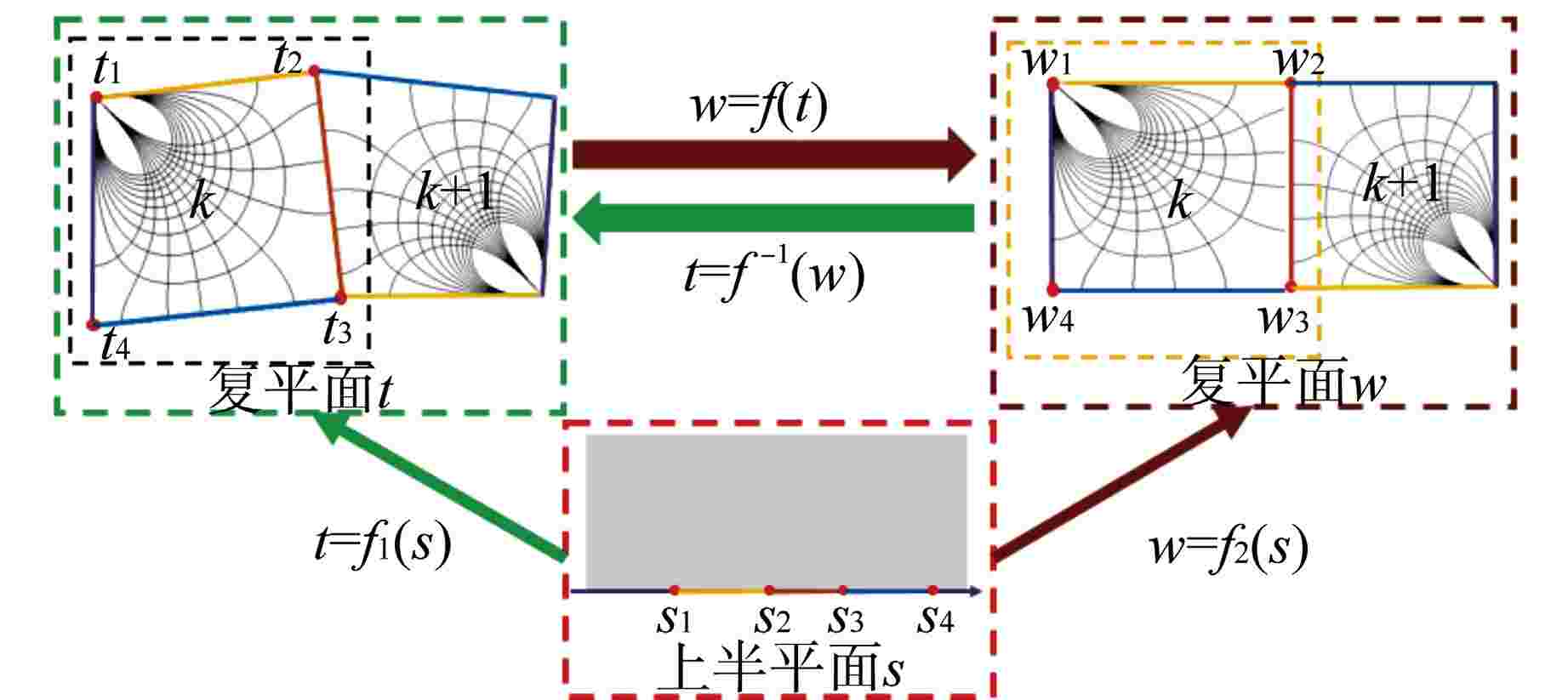
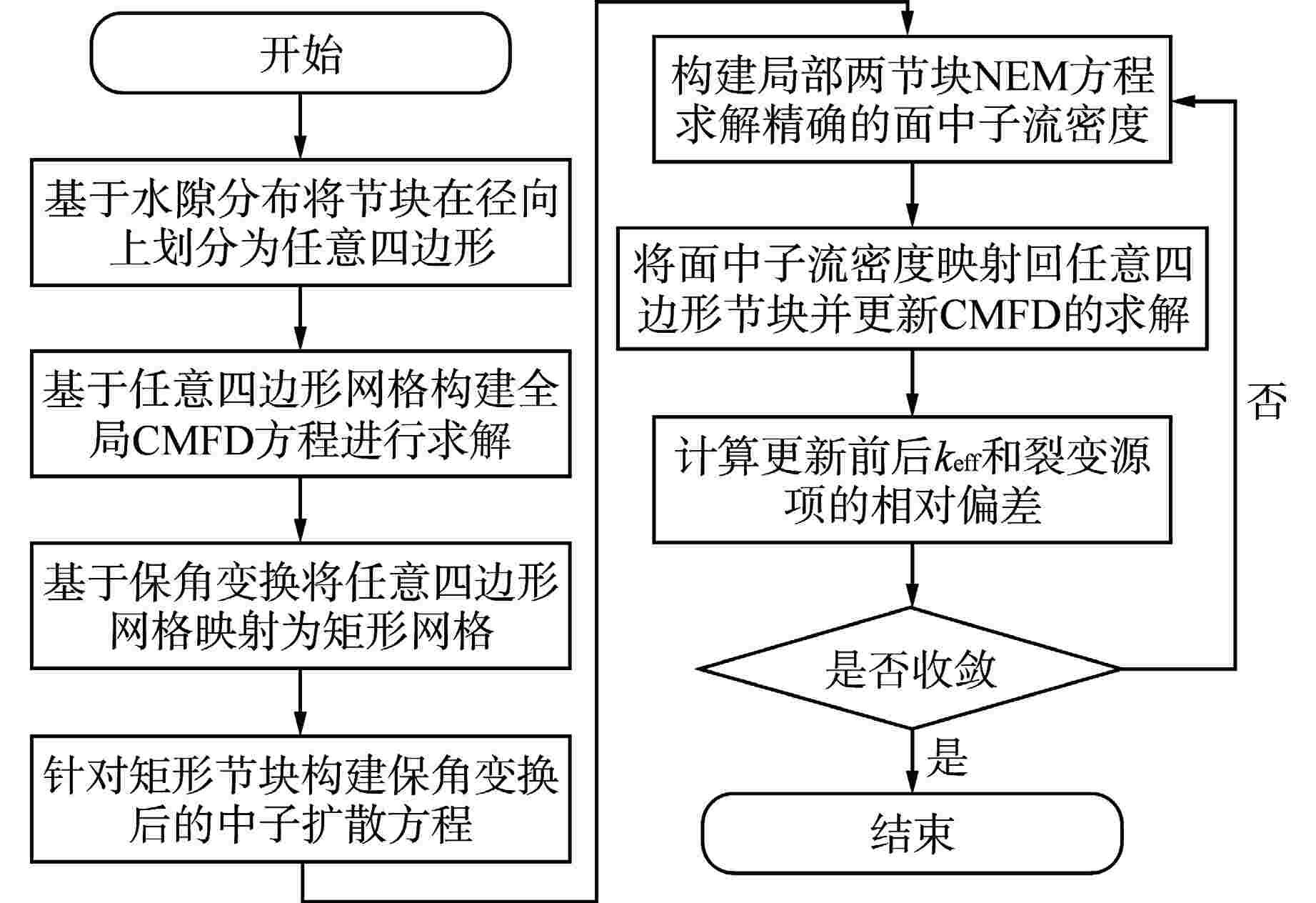
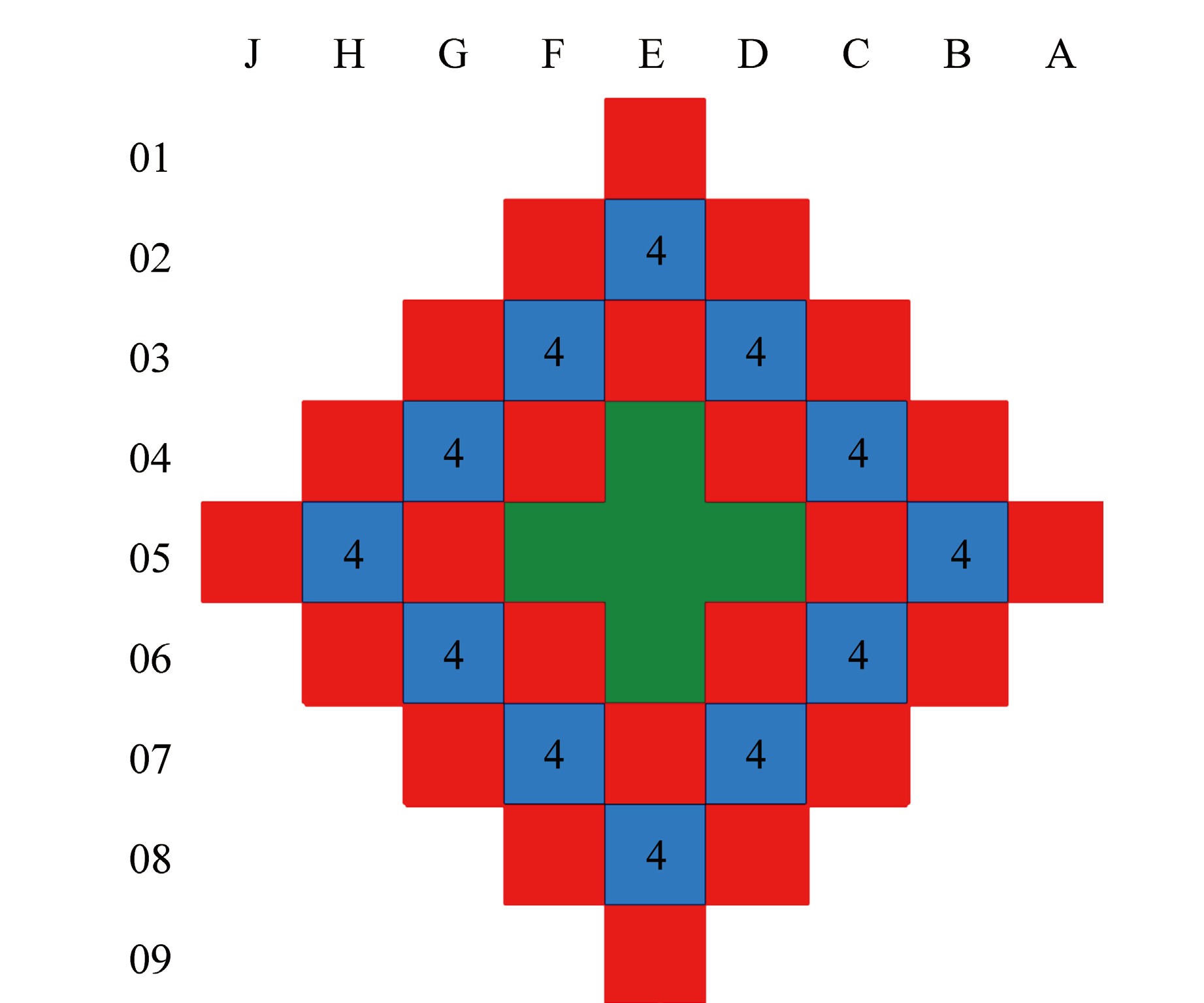
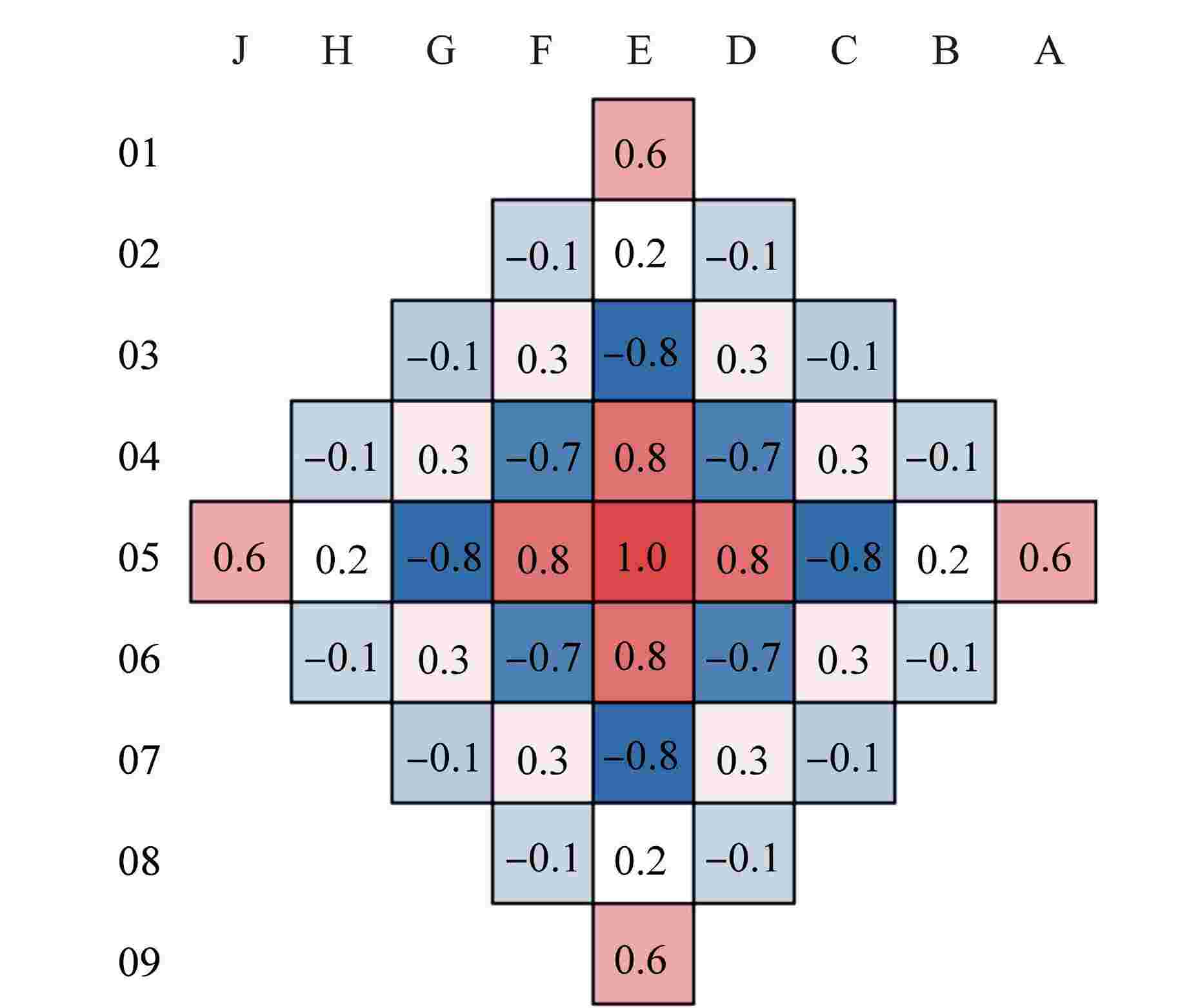
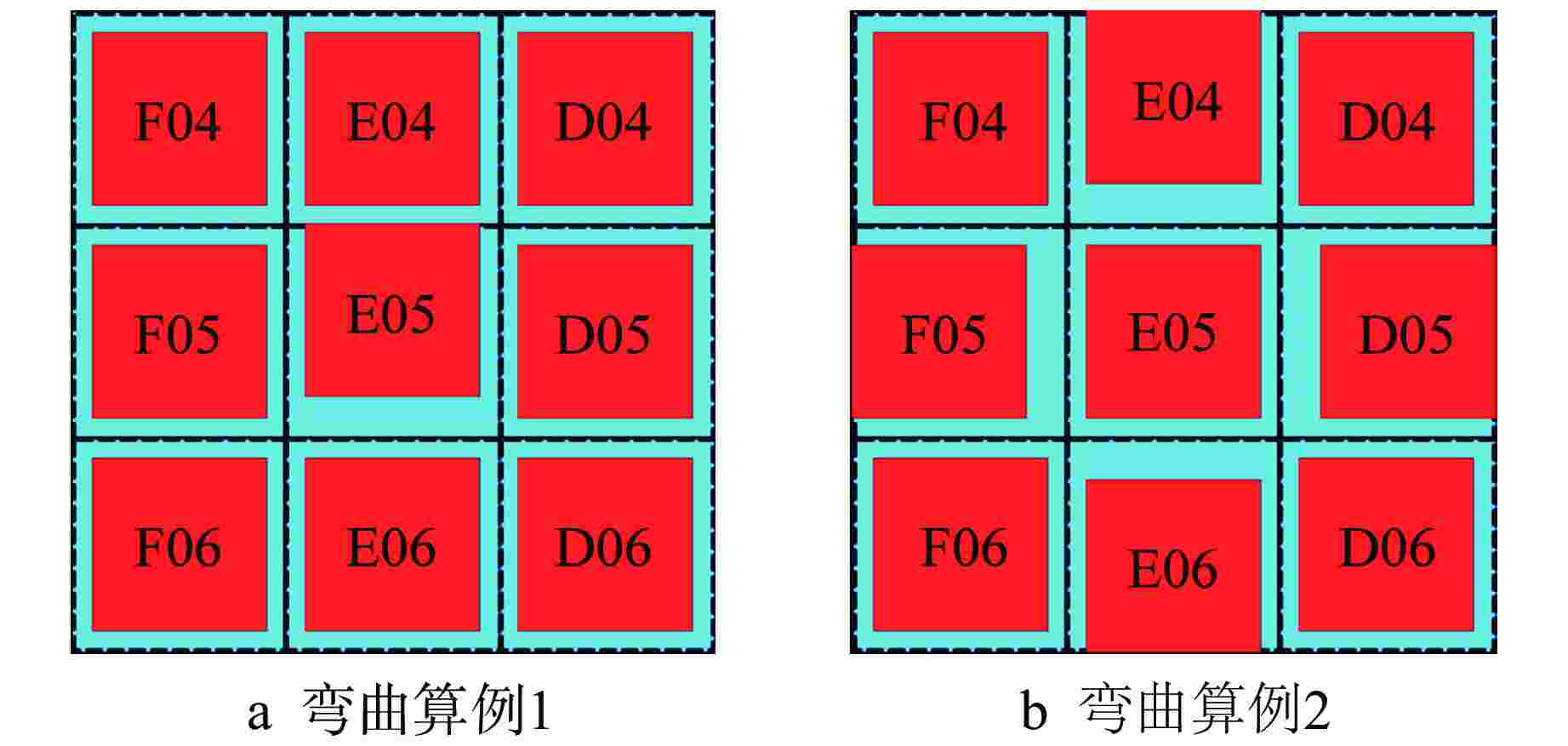
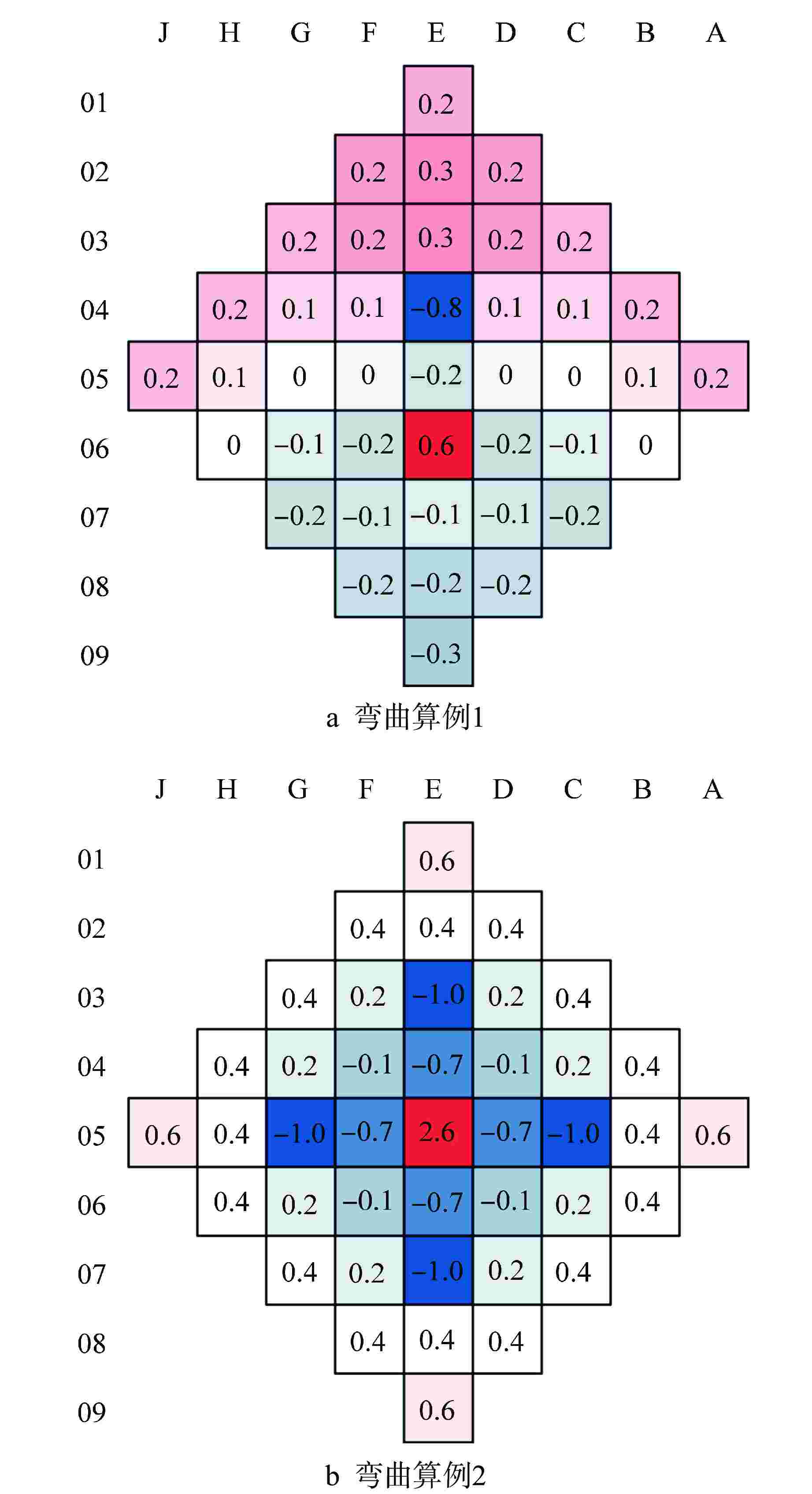
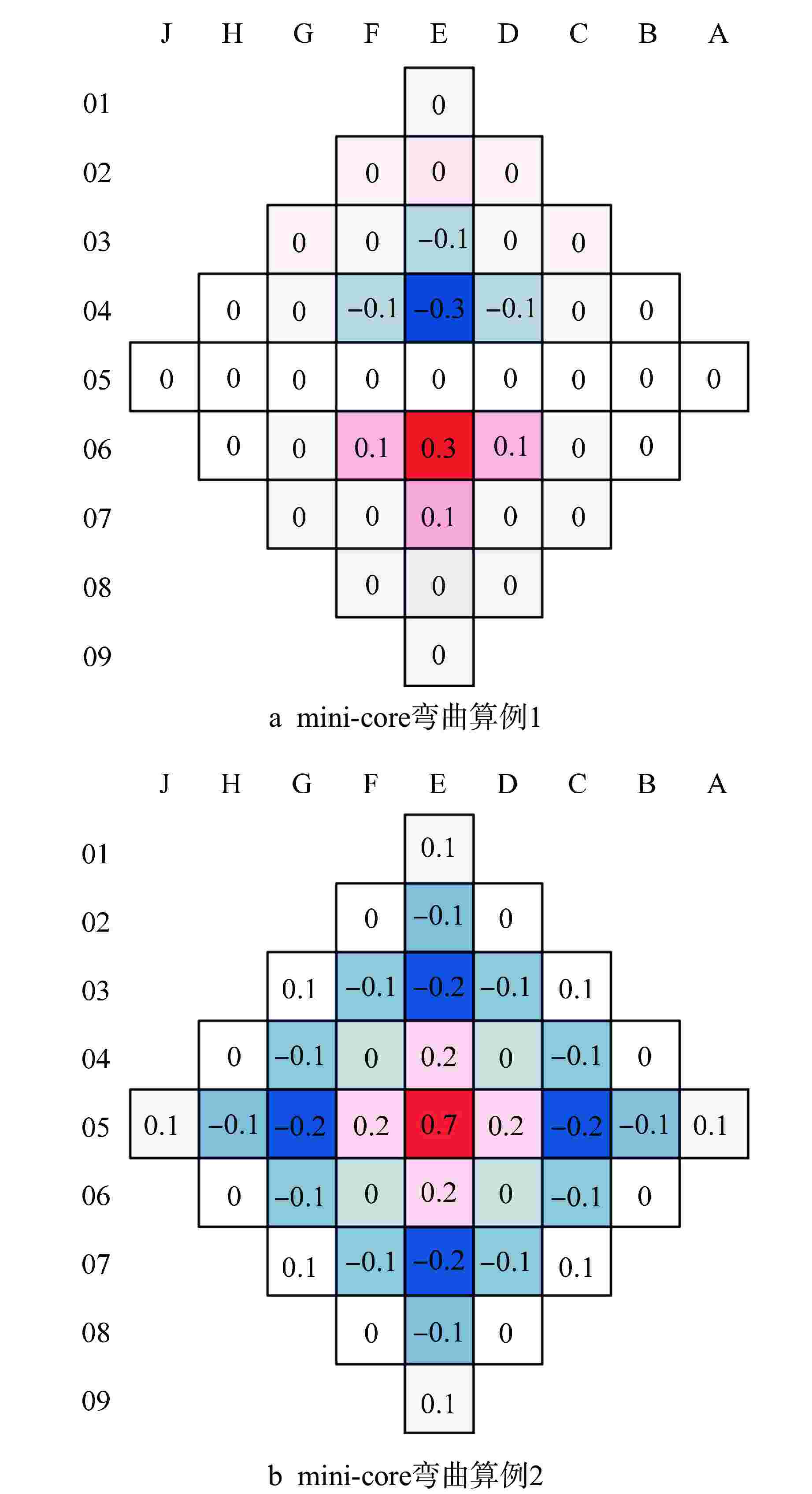
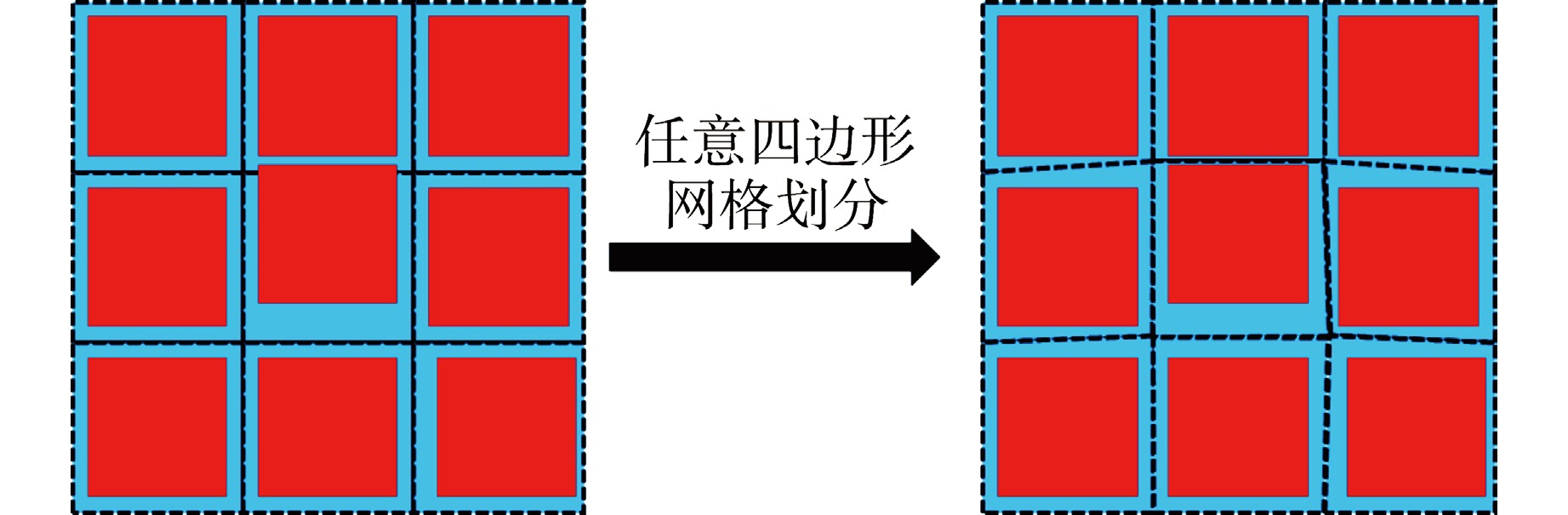
摘要: 为解决传统“横平竖直”的节块网格难以处理压水堆燃料组件弯曲导致的节块网格变形问题，本文根据非线性迭代中子扩散求解思路，开展了基于任意四边形网格和保角变换的中子扩散求解方法研究。采用任意四边形网格刻画燃料组件弯曲导致的节块网格变形现象，建立基于任意四边形网格的全局粗网差分有限方程；采用保角变换将任意四边形变换为矩形，建立基于保角变换的局部两节块展开方程。基于二维mini-core堆芯和华龙一号堆芯构造弯曲算例的计算结果表明：本文所提方法计算弯曲算例的堆芯有效增殖系数（keff）和功率分布结果与NECP-MCX参考解符合较好。因此，本文提出的方法能够较为准确地模拟燃料组件弯曲现象。Abstract: In order to solve the problem that the traditional "horizontal and vertical" nodal grid is difficult to deal with the deformation of nodal grid caused by the bowing of PWR fuel assembly, this paper studies the neutron diffusion solution method based on arbitrary quadrilateral mesh and conformal mapping according to the nonlinear iterative neutron diffusion solution idea. Arbitrary quadrilateral mesh is used to characterize the deformation of nodal grid caused by fuel assembly bowing, and the global coarse mesh difference finite equation based on arbitrary quadrilateral mesh is established. The arbitrary quadrilateral is transformed into rectangle by conformal mapping, and a local two-node expansion equation based on conformal mapping is established. The numerical results of bowing cases based on two-dimensional mini-core and HPR1000 core indicate that, the core effective multiplication factor (keff) and power distribution calculated by the proposed method are in good agreement with the reference NECP-MCX. Therefore, the method proposed in this paper could accurately characterize and simulate the fuel-assembly bowing.
-
Key words:
- Arbitrary quadrilateral mesh /
- Conformal mapping /
- Neutron-diffusion /
- HPR1000
-
图 2 任意四边形网格边界连续
${{l}}_{i+}^k $—第k个节块中心到i正方向面的距离；${{l}}_{i-}^{k+1} $—第(k+1)个节块中心到i负方向面的距离
Figure 2. Continuous Boundary between Quadrilateral Mesh
图 4 结合保角变换的中子扩散非线性迭代流程
Figure 4. Nonlinear Iteration Process for Neutron-diffusion Combined with Conformal Mapping
图 6 二维 mini-core常规模型功率分布相对偏差 %
Figure 6. Relative Bias of Power Distribution for 2D mini-core Normal Model
图 8 NECP-MCX计算二维 mini-core弯曲算例功率分布相对变化 %
Figure 8. Relative Bias of Power Distribution for 2D Mini-core Bowing Cases by NECP-MCX
图 9 改进前的Bamboo-C计算2D mini-core弯曲算例功率分布相对变化 %
Figure 9. Relative Bias of Power Distribution for 2D Mini-core Bowing Cases by Previous Bamboo-C
图 10 改进后的Bamboo-C计算2D mini-core弯曲算例功率分布相对变化 %
Figure 10. Relative Bias of Power Distribution for 2D Mini-core Bowing Cases by Improved Bamboo-C
图 12 华龙一号堆芯常规模型功率分布相对偏差 %
Figure 12. Relative Bias of Power Distribution for HPR1000 Normal Model
图 14 NECP-MCX计算华龙一号弯曲算例功率分布相对变化 %
Figure 14. Relative Bias of Power Distribution for HPR1000 Bowing Cases by NECP-MCX
图 15 改进前的Bamboo-C计算华龙一号弯曲算例功率分布相对变化 %
Figure 15. Relative Bias of Power Distribution for HPR1000 Bowing Cases by Previous Bamboo-C
图 16 改进后的Bamboo-C计算华龙一号弯曲算例功率分布相对变化 %
Figure 16. Relative Bias of Power Distribution for HPR1000 Bowing Cases by Improved Bamboo-C
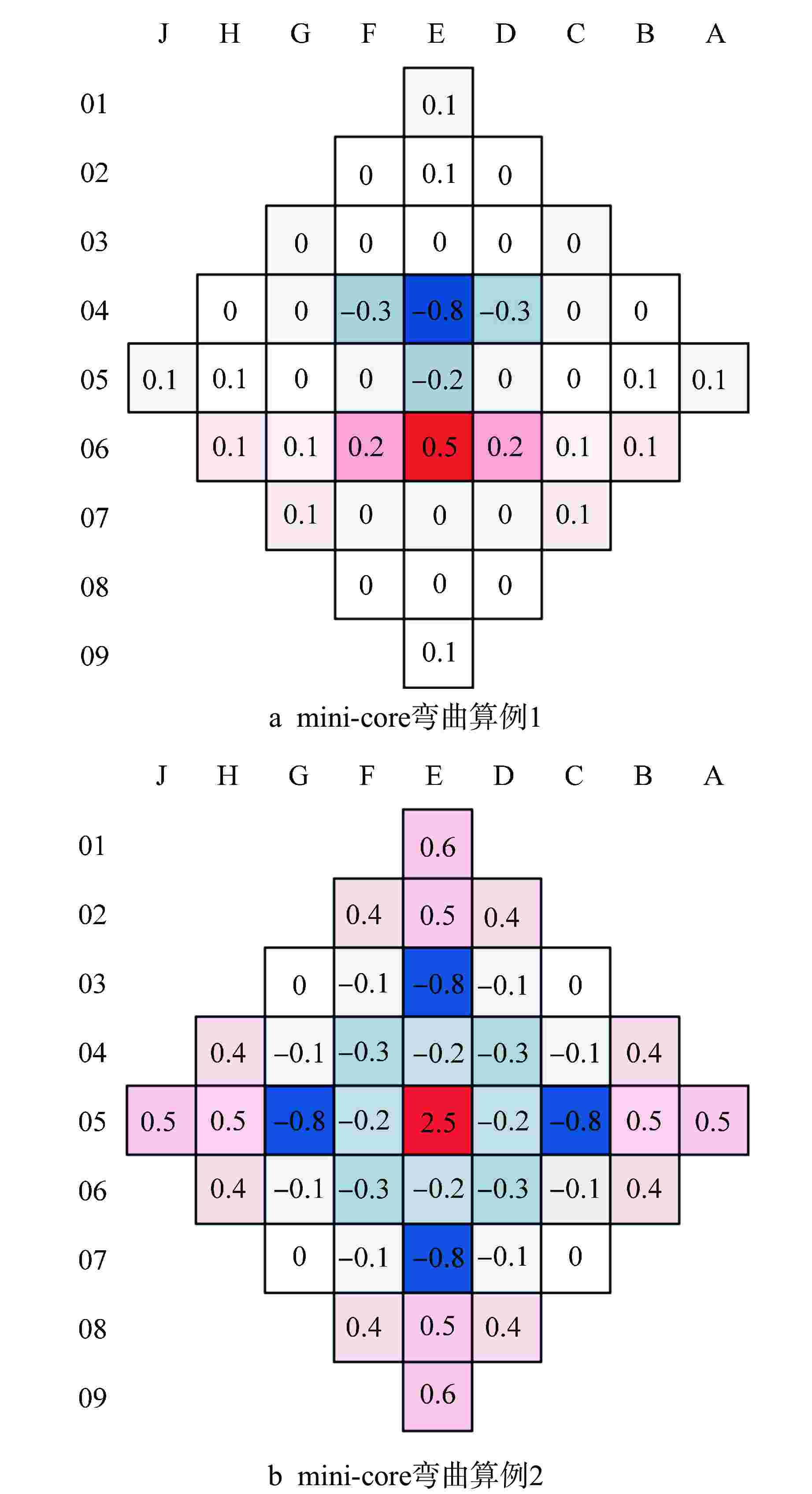
表 1 二维 mini-core弯曲算例keff的对比
Table 1. Comparison of keff for 2D Mini-core Bowing Cases
程序 keff相较于常规模型的变化/pcm 弯曲算例1 弯曲算例2 NECP-MCX −6 −70 改进前的Bamboo-C −0.1 −15 改进后的Bamboo-C −7.3 −44 
下载: 导出CSV
表 2 华龙一号堆芯弯曲算例keff的对比
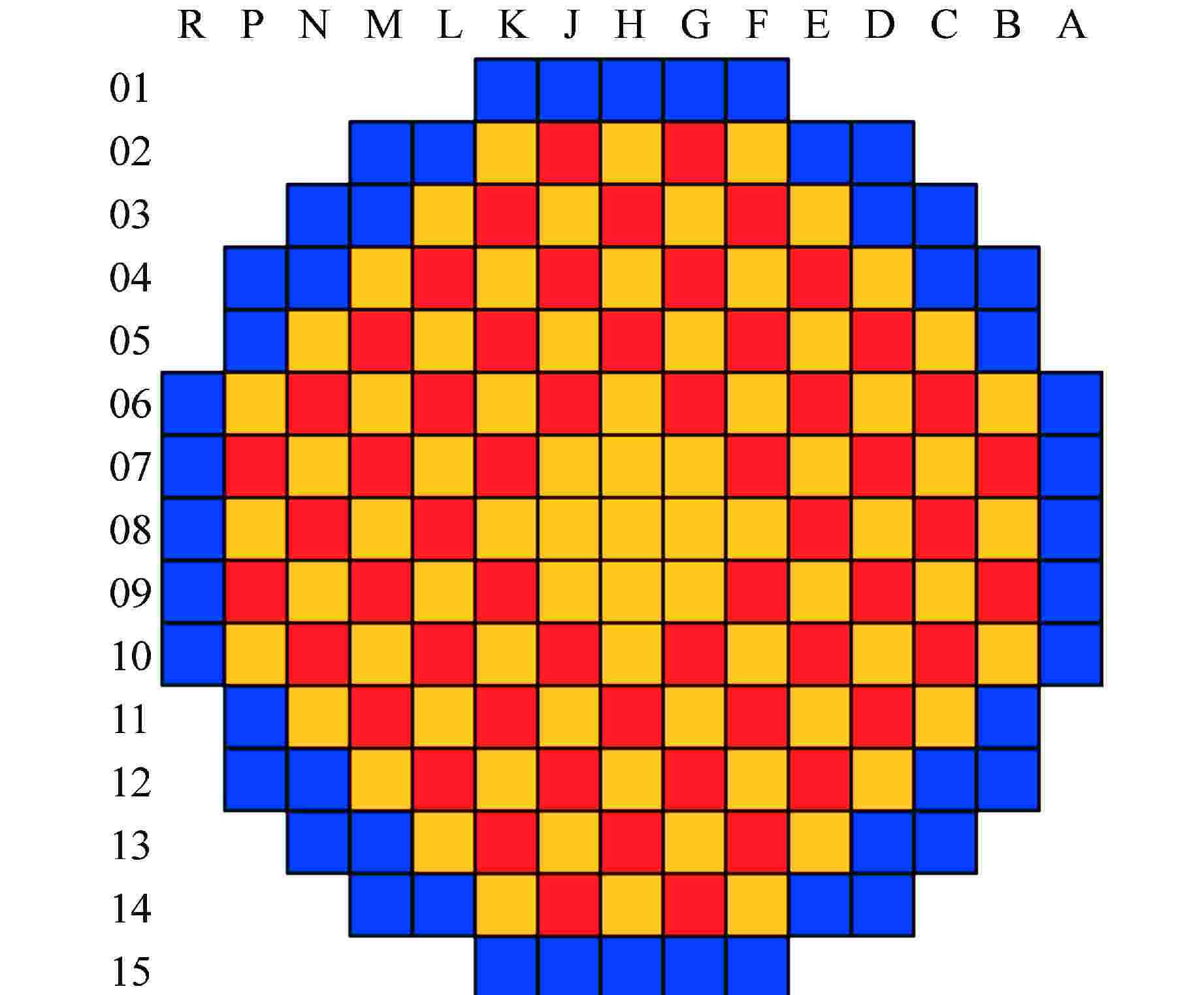
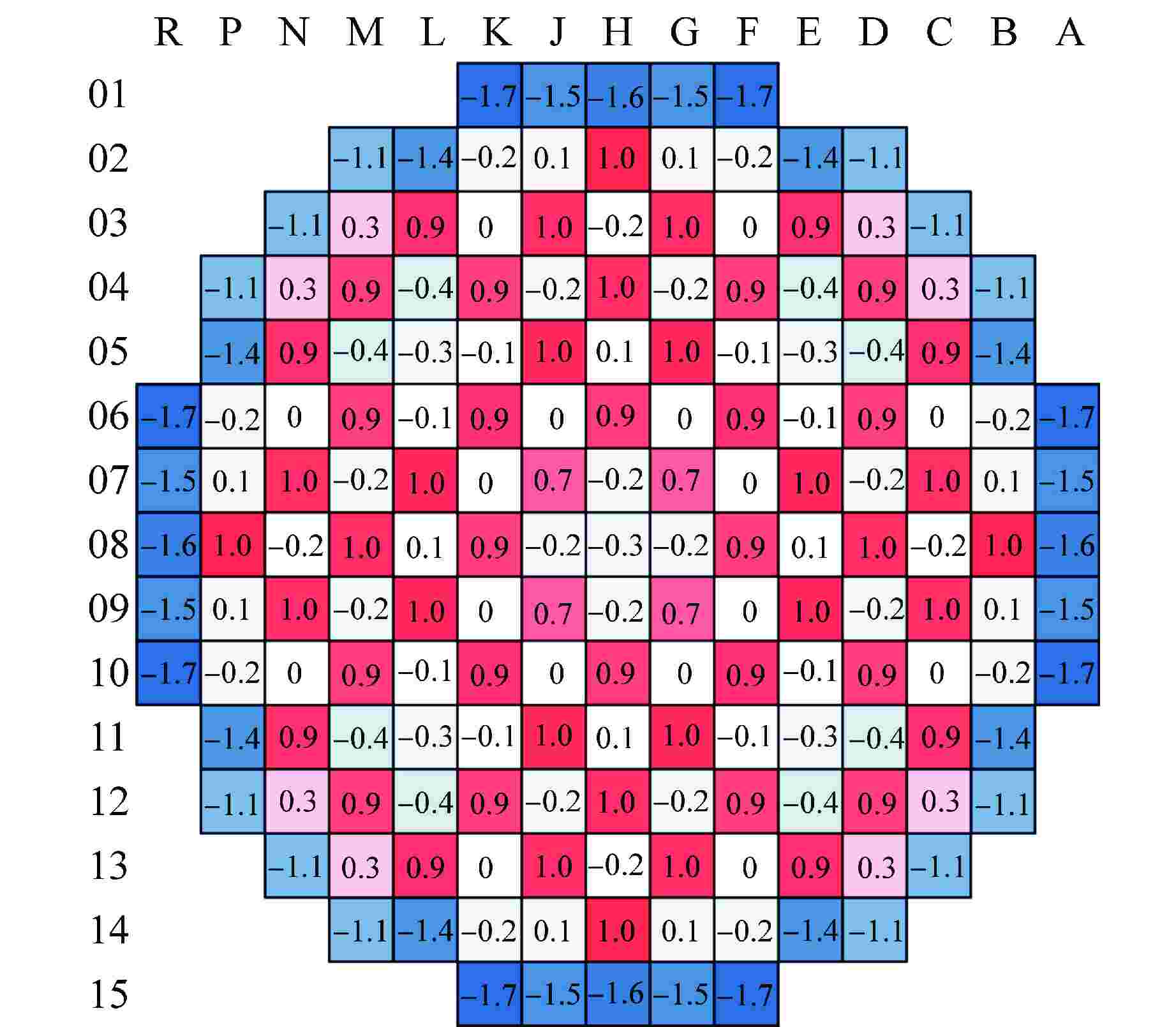
Table 2. Comparison of keff for HPR1000 Bowing Cases
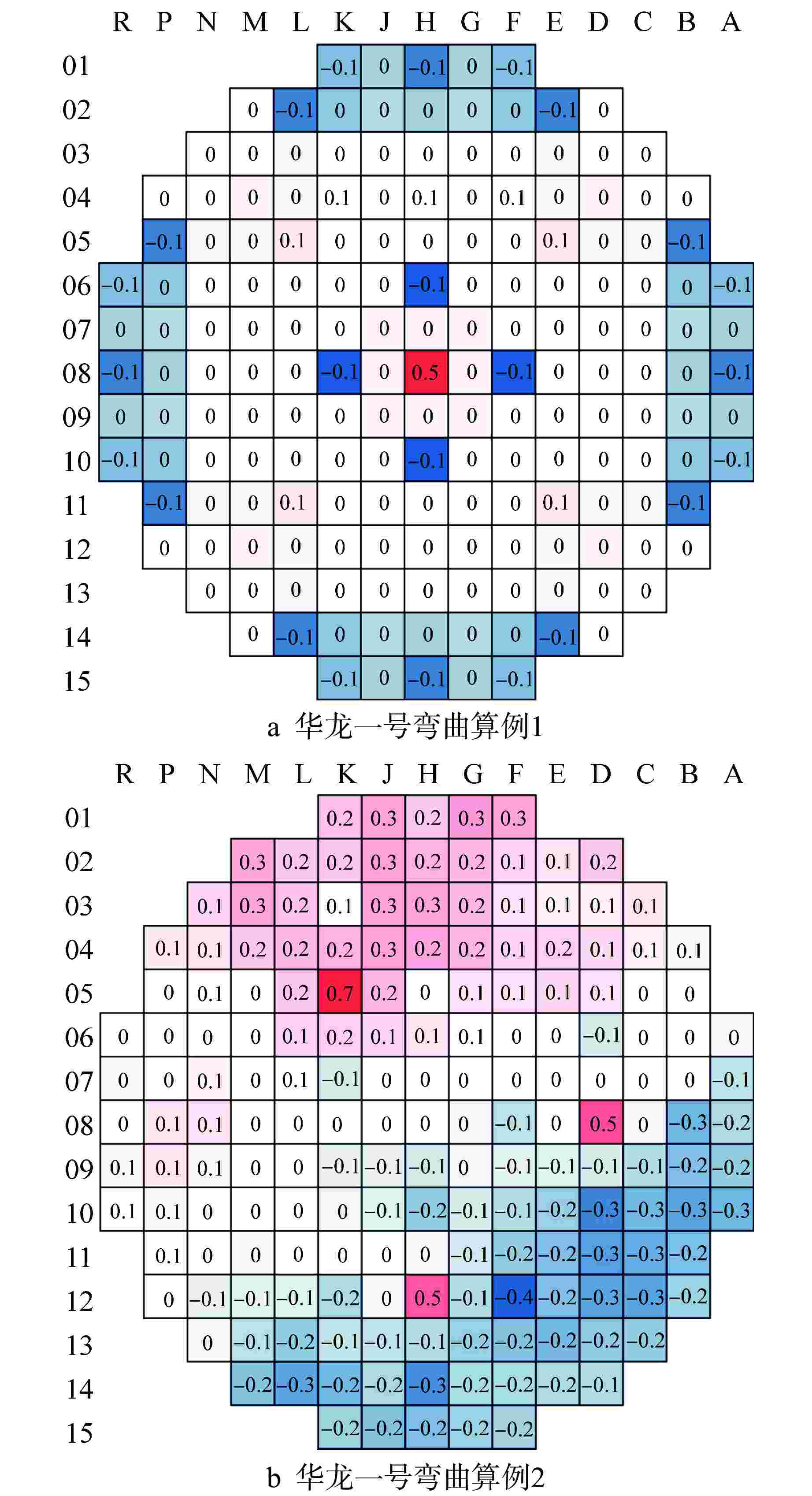
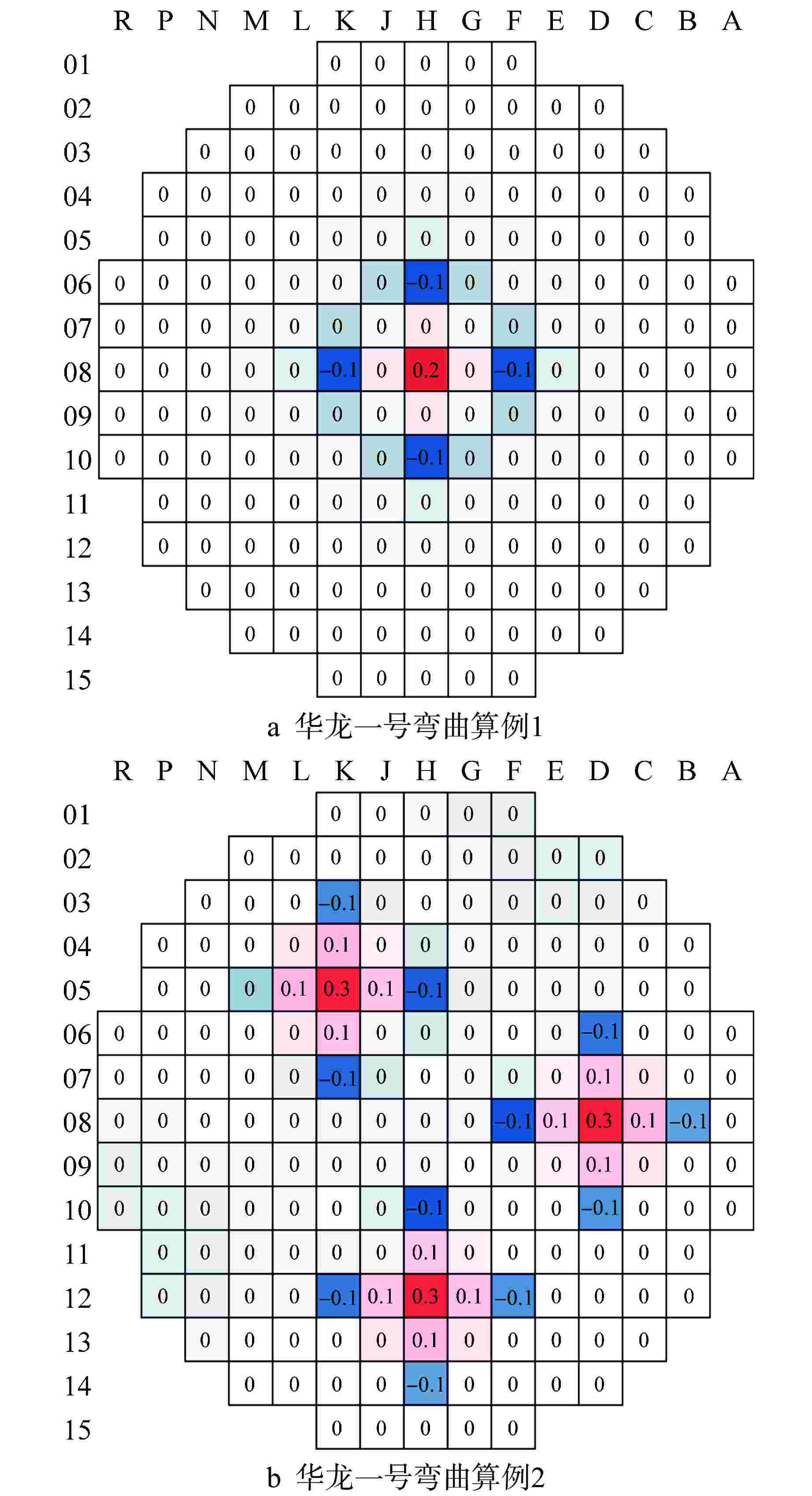
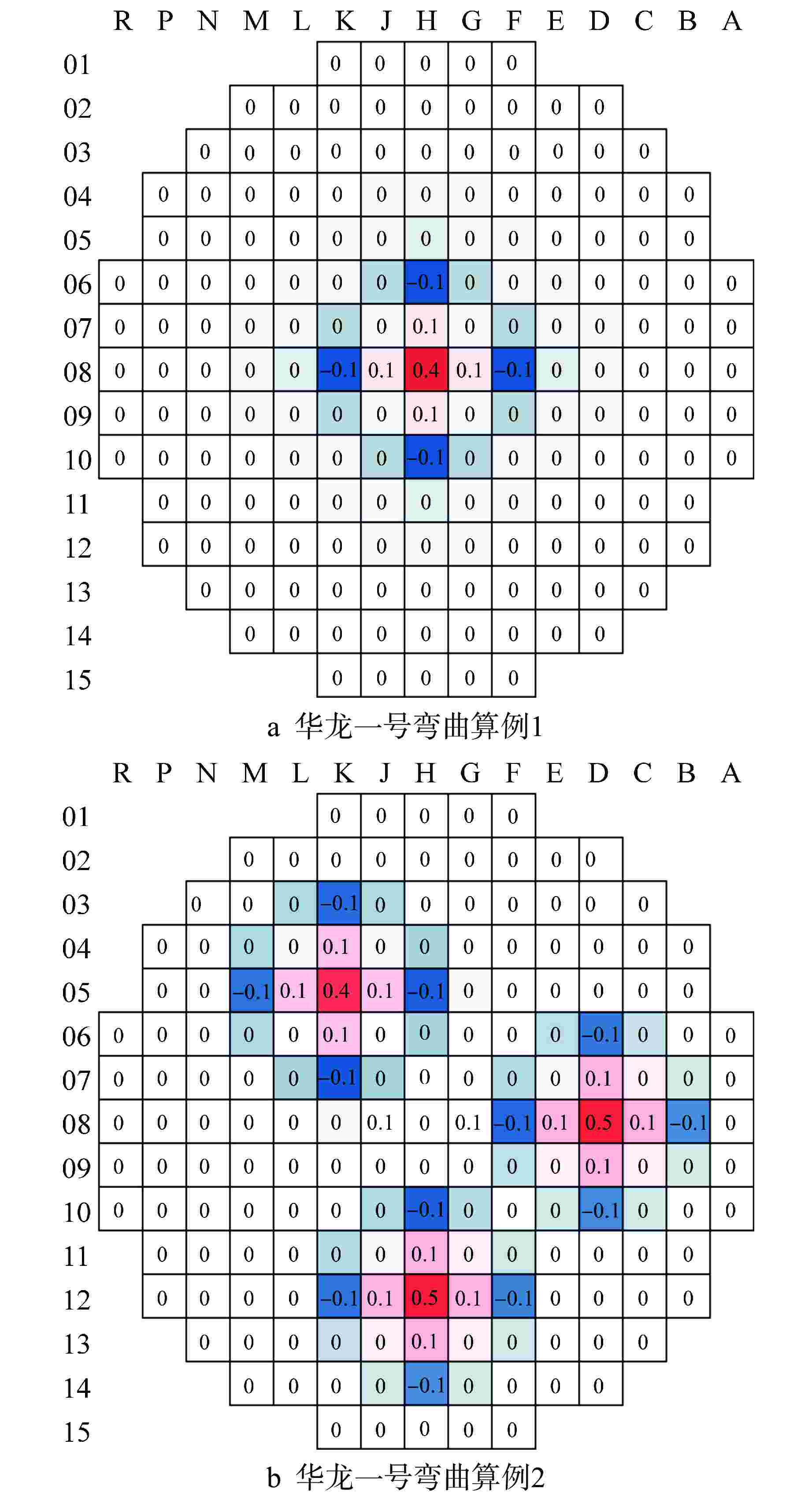
程序 keff相较于常规模型的变化/pcm 弯曲算例1 弯曲算例2 NECP-MCX −0.11 −0.50 改进前的Bamboo-C −0.15 0.30 改进后的Bamboo-C −0.16 0.13
下载: 导出CSV
-
[1] 李伟才,肖忠. 压水堆燃料组件弯曲变形机理及规避措施[J]. 核动力工程,2008, 29(2): 55-57,73. [2] FRANCESCHINI F, FETTERMAN R J, LITTLE D C. Modification of the ANC Nodal Code for analysis of PWR assembly bow[C]//International Conference on the Physics of Reactors 'Nuclear Power: A Sustainable Resource’. Interlaken, Switzerland: Paul Scherrer Institut, 2008. [3] LITTLE D C, FETTERMAN R J. Assembly gap variation methods for the Westinghouse ANC nodal code-13D-01[C]//International Conference on the New Frontiers of Nuclear Technology: Reactor Physics, Safety and High-Performance Computing. Seoul, Korea: American Nuclear Society, 2002. [4] LI J, ROCHMAN D, VASILIEV A, et al. Bowing effects on isotopic concentrations for simplified PWR assemblies and full cores[J]. Annals of Nuclear Energy, 2017, 110: 1023-1029. doi: 10.1016/j.anucene.2017.08.022 [5] ROCHMAN D, MALA P, FERROUKHI H, et al. Bowing effects on power and burn-up distributions for simplified full PWR and BWR cores[C]//International Conference on Mathematics & Computational Methods Applied to Nuclear Science & Engineering. Jeju, Korea: American Nuclear Society, 2017. [6] 厉井钢,王超,陈俊,等. PCM软件包燃料组件弯曲模型的开发及验证[J]. 强激光与粒子束,2022, 34(2): 026004. [7] WAN C H, GUO L, BAI J H. Method research and effect analysis of fuel-assembly bowing on neutron-physics simulations of HPR1000[J]. Annals of Nuclear Energy, 2023, 182: 109616. doi: 10.1016/j.anucene.2022.109616 [8] 万承辉,李云召,郑友琦,等. 压水堆燃料管理软件Bamboo-C研发及工业确认[J]. 核动力工程,2021, 42(5): 15-22. [9] HE Q M, ZHENG Q, LI J, et al. NECP-MCX: a hybrid Monte-Carlo-Deterministic particle-transport code for the simulation of deep-penetration problems[J]. Annals of Nuclear Energy, 2021, 151: 107978. doi: 10.1016/j.anucene.2020.107978 [10] LAWRENCE R D. Progress in nodal methods for the solution of the neutron diffusion and transport equations[J]. Progress in Nuclear Energy, 1986, 17(3): 271-301. doi: 10.1016/0149-1970(86)90034-X [11] CHAO Y A, TSOULFANIDIS N. Conformal mapping and hexagonal nodal methods-I: mathematical foundation[J]. Nuclear Science and Engineering, 1995, 121(2): 202-209. doi: 10.13182/NSE95-A28558 [12] DRISCOLL T A, TREFETHEN L N. Schwarz-christoffel mapping[M]. Cambridge: Cambridge University Press, 2002: 1-8. [13] 崔建斌,姬安召,鲁洪江,等. Schwarz Christoffel变换数值解法[J]. 山东大学学报: 理学版,2016, 51(4): 104-111. [14] 李向阳,刘启伟,李庆,等. 华龙一号反应堆177堆芯核设计[J]. 核动力工程,2019, 40(S1): 8-12. -
计量
- 文章访问数: 23
- HTML全文浏览量: 5
- PDF下载量: 7
- 被引次数: 0
